2018中考数学专题二次函数

2018中考数学专题二次函数

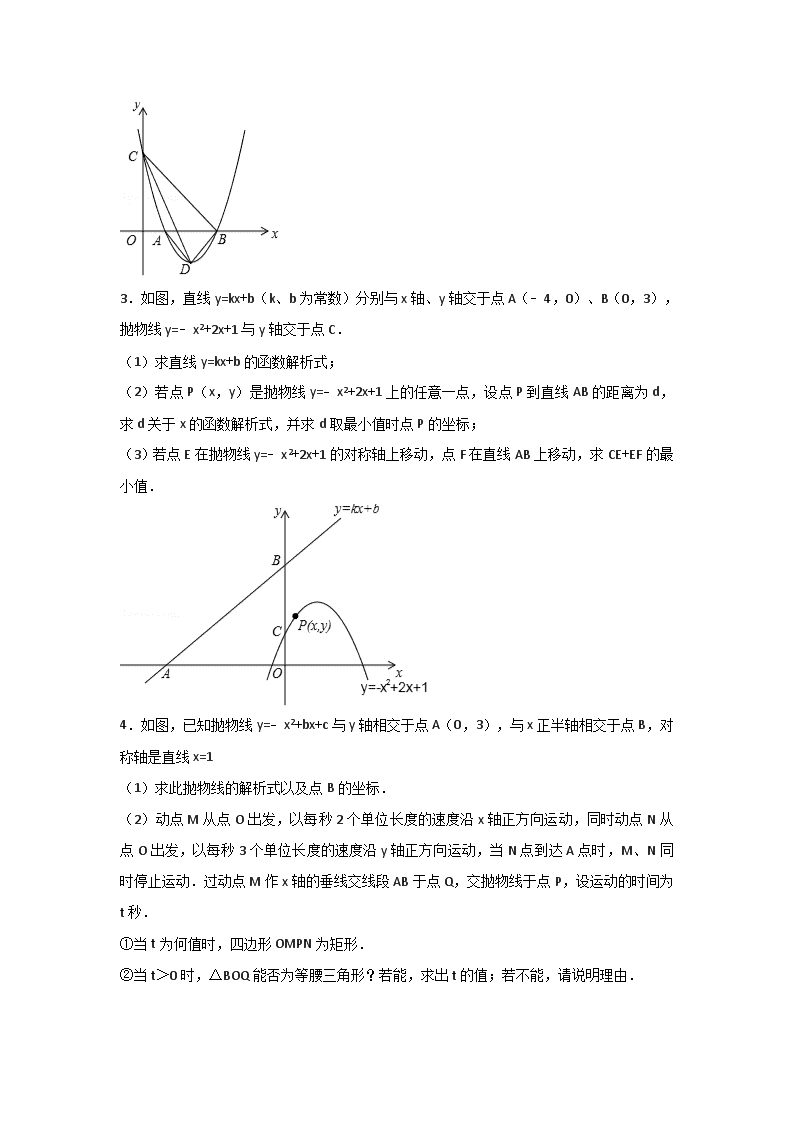
‎2018中考数专题二次函数　‎ ‎（共40题）‎ ‎1．如图，抛物线y=﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y=﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．‎ ‎（1）求抛物线y=﹣x2+bx+c的表达式；‎ ‎（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；‎ ‎（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；‎ ‎②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM它的最小值．‎ ‎2．如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．‎ ‎（1）写出C，D两点的坐标（用含a的式子表示）；‎ ‎（2）设S△BCD：S△ABD=k，求k的值；‎ ‎（3）当△BCD是直角三角形时，求对应抛物线的解析式．‎ ‎3．如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C．‎ ‎（1）求直线y=kx+b的函数解析式；‎ ‎（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的任意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；‎ ‎（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．‎ ‎4．如图，已知抛物线y=﹣x2+bx+c与y轴相交于点A（0，3），与x正半轴相交于点B，对称轴是直线x=1‎ ‎（1）求此抛物线的解析式以及点B的坐标．‎ ‎（2）动点M从点O出发，以每秒2个单位长度的速度沿x轴正方向运动，同时动点N从点O出发，以每秒3个单位长度的速度沿y轴正方向运动，当N点到达A点时，M、N同时停止运动．过动点M作x轴的垂线交线段AB于点Q，交抛物线于点P，设运动的时间为t秒．‎ ‎①当t为何值时，四边形OMPN为矩形．‎ ‎②当t＞0时，△BOQ能否为等腰三角形？若能，求出t的值；若不能，请说明理由．‎ ‎5．如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；‎ ‎（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．‎ ‎6．我们知道，经过原点的抛物线可以用y=ax2+bx（a≠0）表示，对于这样的抛物线：‎ ‎（1）当抛物线经过点（﹣2，0）和（﹣1，3）时，求抛物线的表达式；‎ ‎（2）当抛物线的顶点在直线y=﹣2x上时，求b的值；‎ ‎（3）如图，现有一组这样的抛物线，它们的顶点A1、A2、…，An在直线y=﹣2x上，横坐标依次为﹣1，﹣2，﹣3，…，﹣n（n为正整数，且n≤12），分别过每个顶点作x轴的垂线，垂足记为B1、B2，…，Bn，以线段AnBn为边向左作正方形AnBnCnDn，如果这组抛物线中的某一条经过点Dn，求此时满足条件的正方形AnBnCnDn的边长．‎ ‎7．如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；‎ ‎（3）动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．‎ ‎8．如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）猜想△EDB的形状并加以证明；‎ ‎（3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．‎ ‎9．如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=﹣x2+bx+c经过A、C两点，与x轴的另一交点为点B．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）点D为直线AC上方抛物线上一动点；‎ ‎①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；‎ ‎②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．‎ ‎10．已知二次函数y=﹣x2+bx+c+1，‎ ‎①当b=1时，求这个二次函数的对称轴的方程； ‎ ‎②若c=﹣b2﹣2b，问：b为何值时，二次函数的图象与x轴相切？‎ ‎③若二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜x2，与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足=，求二次函数的表达式．‎ ‎11．如图，抛物线y=﹣x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．‎ ‎（1）求抛物线的解析式及点D的坐标；‎ ‎（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；‎ ‎（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在坐标平面内，以线段MN为对角线作正方形MPNQ，请写出点Q的坐标．‎ ‎12．抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0）．‎ ‎（1）求该抛物线所对应的函数解析式；‎ ‎（2）该抛物线与直线y=x+3相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．‎ ‎①连结PC、PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；‎ ‎②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．‎ ‎13．如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；‎ ‎（3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．‎ ‎14．如图，已知抛物线y=ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．‎ ‎（1）求抛物线的解析式；‎ ‎（2）设点M（1，m），当MB+MD的值最小时，求m的值；‎ ‎（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；‎ ‎（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．‎ ‎15．如图，已知二次函数y=ax2+bx+c（a≠0）的图象经过A（﹣1，0）、B（4，0）、C（0，2）三点．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；‎ ‎（3）点P是该二次函数图象上位于第一象限上的一动点，连接PA分别交BC、y轴于点E、F，若△PEB、△CEF的面积分别为S1、S2，求S1﹣S2的最大值．‎ ‎16．如图，抛物线y=x2+bx+c经过B（﹣1，0），D（﹣2，5）两点，与x轴另一交点为A，点H是线段AB上一动点，过点H的直线PQ⊥x轴，分别交直线AD、抛物线于点Q，P．‎ ‎（1）求抛物线的解析式；‎ ‎（2）是否存在点P，使∠APB=90°，若存在，求出点P的横坐标，若不存在，说明理由；‎ ‎（3）连接BQ，一动点M从点B出发，沿线段BQ以每秒1个单位的速度运动到Q，再沿线段QD以每秒个单位的速度运动到D后停止，当点Q的坐标是多少时，点M在整个运动过程中用时t最少？‎ ‎17．如图1，抛物线C1：y=x2+ax与C2：y=﹣x2+bx相交于点O、C，C1与C2分别交x轴于点B、A，且B为线段AO的中点．‎ ‎（1）求 的值；‎ ‎（2）若OC⊥AC，求△OAC的面积；‎ ‎（3）抛物线C2的对称轴为l，顶点为M，在（2）的条件下：‎ ‎①点P为抛物线C2对称轴l上一动点，当△PAC的周长最小时，求点P的坐标；‎ ‎②如图2，点E在抛物线C2上点O与点M之间运动，四边形OBCE的面积是否存在最大值？若存在，求出面积的最大值和点E的坐标；若不存在，请说明理由．‎ ‎18．如图，已知直角坐标系中，A、B、D三点的坐标分别为A（8，0），B（0，4），D（﹣1，0），点C与点B关于x轴对称，连接AB、AC．‎ ‎（1）求过A、B、D三点的抛物线的解析式；‎ ‎（2）有一动点E从原点O出发，以每秒2个单位的速度向右运动，过点E作x轴的垂线，交抛物线于点P，交线段CA于点M，连接PA、PB，设点E运动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S与t的函数关系式，并求出四边形PBCA的最大面积；‎ ‎（3）抛物线的对称轴上是否存在一点H，使得△‎ ABH是直角三角形？若存在，请直接写出点H的坐标；若不存在，请说明理由．‎ ‎19．如图1，在平面直角坐标系中，已知抛物线y=ax2+bx﹣5与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标；‎ ‎（3）如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；‎ ‎（4）若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．‎ ‎20．如图，已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2，1），并且经过点（4，2），直线y=x+1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C与直线m交于对称轴右侧的点M（t，1），直线m上每一点的纵坐标都等于1．‎ ‎（1）求抛物线的解析式；‎ ‎（2）证明：圆C与x轴相切；‎ ‎（3）过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F，求BE：MF的值．‎ ‎21．如图1，抛物线y=x2+bx+c经过A（﹣2，0）、B（0，﹣2）两点，点C在y轴上，△ABC为等边三角形，点D从点A出发，沿AB方向以每秒2个单位长度的速度向终点B运动，设运动时间为t秒（t＞0），过点D作DE⊥AC于点E，以DE为边作矩形DEGF，使点F在x轴上，点G在AC或AC的延长线上．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将矩形DEGF沿GF所在直线翻折，得矩形D'E'GF，当点D的对称点D'落在抛物线上时，求此时点D'的坐标；‎ ‎（3）如图2，在x轴上有一点M（2，0），连接BM、CM，在点D的运动过程中，设矩形DEGF与四边形ABMC重叠部分的面积为S，直接写出S与t之间的函数关系式，并写出自变量t的取值范围．‎ ‎22．如图，在平面直角坐标系中，△ABC为等腰直角三角形，∠ACB=90°，抛物线y=﹣x2+bx+c经过A，B两点，其中点A，C的坐标分别为（1，0），（﹣4，0），抛物线的顶点为点D．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点E是直角三角形ABC斜边AB上的一个动点（不与A，B重合），过点E作x轴的垂线，交抛物线于点F，当线段FE的长度最大时，求点E的坐标；‎ ‎（3）在（2）的条件下，抛物线上是否存在一点P，使△‎ PEF是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．‎ ‎23．如图1，点A坐标为（2，0），以OA为边在第一象限内作等边△OAB，点C为x轴上一动点，且在点A右侧，连接BC，以BC为边在第一象限内作等边△BCD，连接AD交BC于E．‎ ‎（1）①直接回答：△OBC与△ABD全等吗？‎ ‎②试说明：无论点C如何移动，AD始终与OB平行；‎ ‎（2）当点C运动到使AC2=AE•AD时，如图2，经过O、B、C三点的抛物线为y1．试问：y1上是否存在动点P，使△BEP为直角三角形且BE为直角边？若存在，求出点P坐标；若不存在，说明理由；‎ ‎（3）在（2）的条件下，将y1沿x轴翻折得y2，设y1与y2组成的图形为M，函数y=x+m的图象l与M有公共点．试写出：l与M的公共点为3个时，m的取值．‎ ‎24．如图，抛物线y=ax2﹣2x+c（a≠0）与x轴、y轴分别交于点A，B，C三点，已知点A（﹣2，0），点C（0，﹣8），点D是抛物线的顶点．‎ ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）如图1，抛物线的对称轴与x轴交于点E，第四象限的抛物线上有一点P，将△EBP沿直线EP折叠，使点B的对应点B'落在抛物线的对称轴上，求点P的坐标；‎ ‎（3）如图2，设BC交抛物线的对称轴于点F，作直线CD，点M是直线CD上的动点，点N是平面内一点，当以点B，F，M，N为顶点的四边形是菱形时，请直接写出点M的坐标．‎ ‎25．抛物线y=x2+bx+c与x轴交于A（1，0），B（m，0），与y轴交于C．‎ ‎（1）若m=﹣3，求抛物线的解析式，并写出抛物线的对称轴；‎ ‎（2）如图1，在（1）的条件下，设抛物线的对称轴交x轴于D，在对称轴左侧的抛物线上有一点E，使S△ACE=S△ACD，求点E的坐标；‎ ‎（3）如图2，设F（﹣1，﹣4），FG⊥y于G，在线段OG上是否存在点P，使∠OBP=∠FPG？若存在，求m的取值范围；若不存在，请说明理由．‎ ‎26．如图，⊙M的圆心M（﹣1，2），⊙M经过坐标原点O，与y轴交于点A．经过点A的一条直线l解析式为：y=﹣x+‎ ‎4与x轴交于点B，以M为顶点的抛物线经过x轴上点D（2，0）和点C（﹣4，0）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）求证：直线l是⊙M的切线；‎ ‎（3）点P为抛物线上一动点，且PE与直线l垂直，垂足为E；PF∥y轴，交直线l于点F，是否存在这样的点P，使△PEF的面积最小．若存在，请求出此时点P的坐标及△PEF面积的最小值；若不存在，请说明理由．‎ ‎27．如图，抛物线y=ax2+bx+4交y轴于点A，并经过B（4，4）和C（6，0）两点，点D的坐标为（4，0），连接AD，BC，点E从点A出发，以每秒个单位长度的速度沿线段AD向点D运动，到达点D后，以每秒1个单位长度的速度沿射线DC运动，设点E的运动时间为t秒，过点E作AB的垂线EF交直线AB于点F，以线段EF为斜边向右作等腰直角△EFG．‎ ‎（1）求抛物线的解析式；‎ ‎（2）当点G落在第一象限内的抛物线上时，求出t的值；‎ ‎（3）设点E从点A出发时，点E，F，G都与点A重合，点E在运动过程中，当△BCG的面积为4时，直接写出相应的t值，并直接写出点G从出发到此时所经过的路径长．‎ ‎28．抛物线y=ax2+bx+c过A（2，3），B（4，3），C（6，﹣5）三点．‎ ‎（1）求抛物线的表达式；‎ ‎（2）如图①，抛物线上一点D在线段AC的上方，DE⊥AB交AC于点E，若满足=，求点D的坐标；‎ ‎（3）如图②，F为抛物线顶点，过A作直线l⊥AB，若点P在直线l上运动，点Q在x轴上运动，是否存在这样的点P、Q，使得以B、P、Q为顶点的三角形与△ABF相似，若存在，求P、Q的坐标，并求此时△BPQ的面积；若不存在，请说明理由．‎ ‎29．如图，已知抛物线y=ax2+x+c与x轴交于A，B两点，与y轴交于丁C，且A（2，0），C（0，﹣4），直线l：y=﹣x﹣4与x轴交于点D，点P是抛物线y=ax2+x+c上的一动点，过点P作PE⊥x轴，垂足为E，交直线l于点F．‎ ‎（1）试求该抛物线表达式；‎ ‎（2）如图（1），过点P在第三象限，四边形PCOF是平行四边形，求P点的坐标；‎ ‎（3）如图（2），过点P作PH⊥y轴，垂足为H，连接AC．‎ ‎①求证：△ACD是直角三角形；‎ ‎②试问当P点横坐标为何值时，使得以点P、C、H为顶点的三角形与△ACD相似？‎ ‎30．如图，已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A，B，C三点，其中C（0，3），∠‎ BAC的平分线AE交y轴于点D，交BC于点E，过点D的直线l与射线AC，AB分别交于点M，N．‎ ‎（1）直接写出a的值、点A的坐标及抛物线的对称轴；‎ ‎（2）点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P的坐标；‎ ‎（3）证明：当直线l绕点D旋转时，+均为定值，并求出该定值．‎ ‎31．《函数的图象与性质》拓展学习片段展示：‎ ‎【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣经过原点O，与x轴的另一个交点为A，则a=　 　．‎ ‎【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．‎ ‎【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围．‎ ‎【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围．‎ ‎32．如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数y=x2+bx（b＜0）的图象经过点B，顶点为点D．‎ ‎（1）当t=12时，顶点D到x轴的距离等于　 　；‎ ‎（2）点E是二次函数y=x2+bx（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OE•EA的最大值及取得最大值时的二次函数表达式；‎ ‎（3）矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数y=x2+bx（b＜‎ ‎0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．‎ ‎33．在平面直角坐标系中，直线y=﹣x+1交y轴于点B，交x轴于点A，抛物线y=﹣x2+bx+c经过点B，与直线y=﹣x+1交于点C（4，﹣2）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图，横坐标为m的点M在直线BC上方的抛物线上，过点M作ME∥y轴交直线BC于点E，以ME为直径的圆交直线BC于另一点D，当点E在x轴上时，求△DEM的周长．‎ ‎（3）将△AOB绕坐标平面内的某一点按顺时针方向旋转90°，得到△A1O1B1，点A，O，B的对应点分别是点A1，O1，B1，若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的坐标．‎ ‎34．已知，抛物线y=ax2+bx+3（a＜0）与x轴交于A（3，0）、B两点，与y轴交于点C，抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE=．‎ ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）求证：直线DE是△ACD外接圆的切线；‎ ‎（3）在直线AC上方的抛物线上找一点P，使S△ACP=S△ACD，求点P的坐标；‎ ‎（4）在坐标轴上找一点M，使以点B、C、M为顶点的三角形与△‎ ACD相似，直接写出点M的坐标．‎ ‎35．如图①，在平面直角坐标系中，二次函数y=﹣x2+bx+c的图象与坐标轴交于A，B，C三点，其中点A的坐标为（﹣3，0），点B的坐标为（4，0），连接AC，BC．动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒．连接PQ．‎ ‎（1）填空：b=　 　，c=　 　；‎ ‎（2）在点P，Q运动过程中，△APQ可能是直角三角形吗？请说明理由；‎ ‎（3）在x轴下方，该二次函数的图象上是否存在点M，使△PQM是以点P为直角顶点的等腰直角三角形？若存在，请求出运动时间t；若不存在，请说明理由；‎ ‎（4）如图②，点N的坐标为（﹣，0），线段PQ的中点为H，连接NH，当点Q关于直线NH的对称点Q′恰好落在线段BC上时，请直接写出点Q′的坐标．‎ ‎36．如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线 y=﹣x2+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以每秒1个单位的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以每秒个单位的速度匀速运动，连接PQ，设运动时间为t秒．‎ ‎（1）求抛物线的解析式；‎ ‎（2）问：当t为何值时，△APQ为直角三角形；‎ ‎（3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；‎ ‎（4）设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．‎ ‎37．如图，直线y=﹣x+3与x轴，y轴分别相交于点B，C，经过B，C两点的抛物线y=ax2+bx+c与x轴的另一交点为A，顶点为P，且对称轴是直线x=2．‎ ‎（1）求该抛物线的函数表达式；‎ ‎（2）请问在抛物线上是否存在点Q，使得以点B，C，Q为顶点的三角形为直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由；‎ ‎（3）过S（0，4）的动直线l交抛物线于M，N两点，试问抛物线上是否存在定点T，使得不过定点T的任意直线l都有∠MTN=90°？若存在，请求出点T的坐标；若不存在，请说明理由．‎ ‎38．如图，抛物线C1：y1=ax2+2ax（a＞0）与x轴交于点A，顶点为点P．‎ ‎（1）直接写出抛物线C1的对称轴是　 　，用含a的代数式表示顶点P的坐标　 　；‎ ‎（2）把抛物线C1绕点M（m，0）旋转180°得到抛物线C2（其中m＞0），抛物线C2与x轴右侧的交点为点B，顶点为点Q．‎ ‎①当m=1时，求线段AB的长；‎ ‎②在①的条件下，是否存在△ABP为等腰三角形，若存在请求出a的值，若不存在，请说明理由；‎ ‎③当四边形APBQ为矩形时，请求出m与a之间的数量关系，并直接写出当a=3时矩形APBQ的面积．‎ ‎39．已知二次函数y=ax2﹣4ax+a2+2（a＜0）图象的顶点G在直线AB上，其中 A（﹣，0）、B（0，3），对称轴与x轴交于点E．‎ ‎（1）求二次函数y=ax2﹣4ax+a2+2的关系式；‎ ‎（2）点P在对称轴右侧的抛物线上，且AP平分四边形GAEP的面积，求点P坐标；‎ ‎（3）在x轴上方，是否存在整数m，使得当＜x≤时，抛物线y随x增大而增大？若存在，求出所有满足条件的m值；若不存在，请说明理由．‎ ‎40．如图，在平面直角坐标系中，点O为坐标原点，抛物线y=x2+bx+c交x轴于A、B两点，交y轴于点C，直线y=x﹣3经过B、C两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）过点C作直线CD⊥y轴交抛物线于另一点D，点P是直线CD下方抛物线上的一个动点，且在抛物线对称轴的右侧，过点P作PE⊥x轴于点E，PE交CD于点F，交BC于点M，连接AC，过点M作MN⊥AC于点N，设点P的横坐标为t，线段MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；‎ ‎（3）在（2）的条件下，连接PC，过点B作BQ⊥PC于点Q（点Q在线段PC上），BQ交CD于点T，连接OQ交CD于点S，当ST=TD时，求线段MN的长．‎ ‎　‎ 参考答案与试题解析 ‎（共40题）‎ ‎1．（2017•兰州）如图，抛物线y=﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y=﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．‎ ‎（1）求抛物线y=﹣x2+bx+c的表达式；‎ ‎（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；‎ ‎（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；‎ ‎②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM它的最小值．‎ ‎【解答】解：（1）∵点A（﹣4，﹣4），B（0，4）在抛物线y=﹣x2+bx+c上，‎ ‎∴，‎ ‎∴，‎ ‎∴抛物线的解析式为y=﹣x2﹣2x+4；‎ ‎（2）设直线AB的解析式为y=kx+n过点A，B，‎ ‎∴，‎ ‎∴，‎ ‎∴直线AB的解析式为y=2x+4，‎ 设E（m，2m+4），‎ ‎∴G（m，﹣m2﹣2m+4），‎ ‎∵四边形GEOB是平行四边形，‎ ‎∴EG=OB=4，‎ ‎∴|﹣m2﹣2m+4﹣2m﹣4|=4，‎ ‎∴m=﹣2或m=2+2或m=2﹣2，‎ ‎∴G（﹣2，4）或（2+2，﹣12﹣12）或（2﹣2，﹣12+12）．‎ ‎（3）①如图1，‎ 由（2）知，直线AB的解析式为y=2x+4，‎ ‎∴设E（a，2a+4），‎ ‎∵直线AC：y=﹣x﹣6，‎ ‎∴F（a，﹣a﹣6），‎ 设H（0，p），‎ ‎∵以点A，E，F，H为顶点的四边形是矩形，‎ ‎∵直线AB的解析式为y=2x+4，直线AC：y=﹣x﹣6，‎ ‎∴AB⊥AC，‎ ‎∴EF为对角线，‎ ‎∴（﹣4+0）=（a+a），（﹣4+p）=（2a+4﹣a﹣6），‎ ‎∴a=﹣2，P=﹣1，‎ ‎∴E（﹣2，0）．H（0，﹣1）；‎ ‎②如图2，‎ 由①知，E（﹣2，0），H（0，﹣1），A（﹣4，﹣4），‎ ‎∴EH=，AE=2，‎ 设AE交⊙E于G，取EG的中点P，‎ ‎∴PE=，‎ 连接PC交⊙E于M，连接EM，‎ ‎∴EM=EH=，‎ ‎∴=，‎ ‎∵=，‎ ‎∴=，∵∠PEM=∠MEA，‎ ‎∴△PEM∽△MEA，‎ ‎∴，‎ ‎∴PM=AM，‎ ‎∴AM+CM的最小值=PC，‎ 设点P（p，2p+4），‎ ‎∵E（﹣2，0），‎ ‎∴PE2=（p+2）2+（2p+4）2=5（p+2）2，‎ ‎∵PE=，‎ ‎∴5（p+2）2=，‎ ‎∴p=﹣或p=﹣（由于E（﹣2，0），所以舍去），‎ ‎∴P（﹣，﹣1），‎ ‎∵C（0，﹣6），‎ ‎∴PC==，‎ 即：AM+CM=．‎ ‎2．（2017•贵港）如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．‎ ‎（1）写出C，D两点的坐标（用含a的式子表示）；‎ ‎（2）设S△BCD：S△ABD=k，求k的值；‎ ‎（3）当△BCD是直角三角形时，求对应抛物线的解析式．‎ ‎【解答】解：‎ ‎（1）在y=a（x﹣1）（x﹣3），令x=0可得y=3a，‎ ‎∴C（0，3a），‎ ‎∵y=a（x﹣1）（x﹣3）=a（x2﹣4x+3）=a（x﹣2）2﹣a，‎ ‎∴D（2，﹣a）；‎ ‎（2）在y=a（x﹣1）（x﹣3）中，令y=0可解得x=1或x=3，‎ ‎∴A（1，0），B（3，0），‎ ‎∴AB=3﹣1=2，‎ ‎∴S△ABD=×2×a=a，‎ 如图，设直线CD交x轴于点E，设直线CD解析式为y=kx+b，‎ 把C、D的坐标代入可得，解得，‎ ‎∴直线CD解析式为y=﹣2ax+3a，令y=0可解得x=，‎ ‎∴E（，0），‎ ‎∴BE=3﹣=‎ ‎∴S△BCD=S△BEC+S△BED=××（3a+a）=3a，‎ ‎∴S△BCD：S△ABD=（3a）：a=3，‎ ‎∴k=3；‎ ‎（3）∵B（3，0），C（0，3a），D（2，﹣a），‎ ‎∴BC2=32+（3a）2=9+9a2，CD2=22+（﹣a﹣3a）2=4+16a2，BD2=（3﹣2）2+a2=1+a2，‎ ‎∵∠BCD＜∠BCO＜90°，‎ ‎∴△BCD为直角三角形时，只能有∠CBD=90°或∠CDB=90°两种情况，‎ ‎①当∠CBD=90°时，则有BC2+BD2=CD2，即9+9a2+1+a2=4+16a2，解得a=﹣1（舍去）或a=1，此时抛物线解析式为y=x2﹣4x+3；‎ ‎②当∠CDB=90°时，则有CD2+BD2=BC2，即4+16a2+1+a2=9+9a2，解得a=﹣（舍去）或a=，此时抛物线解析式为y=x2﹣2x+；‎ 综上可知当△BCD是直角三角形时，抛物线的解析式为y=x2﹣4x+3或y=x2﹣2x+．‎ ‎3．（2017•滨州）如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C．‎ ‎（1）求直线y=kx+b的函数解析式；‎ ‎（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的任意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；‎ ‎（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．‎ ‎【解答】解：‎ ‎（1）由题意可得，解得，‎ ‎∴直线解析式为y=x+3；‎ ‎（2）如图1，过P作PH⊥AB于点H，过H作HQ⊥x轴，过P作PQ⊥y轴，两垂线交于点Q，‎ 则∠AHQ=∠ABO，且∠AHP=90°，‎ ‎∴∠PHQ+∠AHQ=∠BAO+∠ABO=90°，‎ ‎∴∠PHQ=∠BAO，且∠AOB=∠PQH=90°，‎ ‎∴△PQH∽△BOA，‎ ‎∴==，‎ 设H（m，m+3），则PQ=x﹣m，HQ=m+3﹣（﹣x2+2x+1），‎ ‎∵A（﹣4，0），B（0，3），‎ ‎∴OA=4，OB=3，AB=5，且PH=d，‎ ‎∴==，‎ 整理消去m可得d=x2﹣x+=（x﹣）2+，‎ ‎∴d与x的函数关系式为d=（x﹣）2+，‎ ‎∵＞0，‎ ‎∴当x=时，d有最小值，此时y=﹣（）2+2×+1=，‎ ‎∴当d取得最小值时P点坐标为（，）；‎ ‎（3）如图2，设C点关于抛物线对称轴的对称点为C′，由对称的性质可得CE=C′E，‎ ‎∴CE+EF=C′E+EF，‎ ‎∴当F、E、C′三点一线且C′F与AB垂直时CE+EF最小，‎ ‎∵C（0，1），‎ ‎∴C′（2，1），‎ 由（2）可知当x=2时，d=×（2﹣）2+=，‎ 即CE+EF的最小值为．‎ ‎4．（2017•广安）如图，已知抛物线y=﹣x2+bx+c与y轴相交于点A（0，3），与x正半轴相交于点B，对称轴是直线x=1‎ ‎（1）求此抛物线的解析式以及点B的坐标．‎ ‎（2）动点M从点O出发，以每秒2个单位长度的速度沿x轴正方向运动，同时动点N从点O出发，以每秒3个单位长度的速度沿y轴正方向运动，当N点到达A点时，M、N同时停止运动．过动点M作x轴的垂线交线段AB于点Q，交抛物线于点P，设运动的时间为t秒．‎ ‎①当t为何值时，四边形OMPN为矩形．‎ ‎②当t＞0时，△BOQ能否为等腰三角形？若能，求出t的值；若不能，请说明理由．‎ ‎【解答】解：‎ ‎（1）∵抛物线y=﹣x2+bx+c对称轴是直线x=1，‎ ‎∴﹣=1，解得b=2，‎ ‎∵抛物线过A（0，3），‎ ‎∴c=3，‎ ‎∴抛物线解析式为y=﹣x2+2x+3，‎ 令y=0可得﹣x2+2x+3=0，解得x=﹣1或x=3，‎ ‎∴B点坐标为（3，0）；‎ ‎（2）①由题意可知ON=3t，OM=2t，‎ ‎∵P在抛物线上，‎ ‎∴P（2t，﹣4t2+4t+3），‎ ‎∵四边形OMPN为矩形，‎ ‎∴ON=PM，‎ ‎∴3t=﹣4t2+4t+3，解得t=1或t=﹣（舍去），‎ ‎∴当t的值为1时，四边形OMPN为矩形；‎ ‎②∵A（0，3），B（3，0），‎ ‎∴OA=OB=3，且可求得直线AB解析式为y=﹣x+3，‎ ‎∴当t＞0时，OQ≠OB，‎ ‎∴当△BOQ为等腰三角形时，有OB=QB或OQ=BQ两种情况，‎ 由题意可知OM=2t，‎ ‎∴Q（2t，﹣2t+3），‎ ‎∴OQ==，BQ==|2t﹣3|，‎ 又由题意可知0＜t＜1，‎ 当OB=QB时，则有|2t﹣3|=3，解得t=（舍去）或t=；‎ 当OQ=BQ时，则有=|2t﹣3|，解得t=；‎ 综上可知当t的值为或时，△BOQ为等腰三角形．‎ ‎5．（2017•宜宾）如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；‎ ‎（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．‎ ‎【解答】解：‎ ‎（1）∵抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点，‎ ‎∴，解得，‎ ‎∴抛物线解析式为y=﹣x2+4x+5；‎ ‎（2）∵AD=5，且OA=1，‎ ‎∴OD=6，且CD=8，‎ ‎∴C（﹣6，8），‎ 设平移后的点C的对应点为C′，则C′点的纵坐标为8，‎ 代入抛物线解析式可得8=﹣x2+4x+5，解得x=1或x=3，‎ ‎∴C′点的坐标为（1，8）或（3，8），‎ ‎∵C（﹣6，8），‎ ‎∴当点C落在抛物线上时，向右平移了7或9个单位，‎ ‎∴m的值为7或9；‎ ‎（3）∵y=﹣x2+4x+5=﹣（x﹣2）2+9，‎ ‎∴抛物线对称轴为x=2，‎ ‎∴可设P（2，t），‎ 由（2）可知E点坐标为（1，8），‎ ‎①当BE为平行四边形的边时，连接BE交对称轴于点M，过E作EF⊥x轴于点F，过Q作对称轴的垂线，垂足为N，如图，‎ 则∠BEF=∠BMP=∠QPN，‎ 在△PQN和△EFB中 ‎∴△PQN≌△EFB（AAS），‎ ‎∴NQ=BF=OB﹣OF=5﹣1=4，‎ 设Q（x，y），则QN=|x﹣2|，‎ ‎∴|x﹣2|=4，解得x=﹣2或x=6，‎ 当x=﹣2或x=6时，代入抛物线解析式可求得y=﹣7，‎ ‎∴Q点坐标为（﹣2，﹣7）或（6，﹣7）；‎ ‎②当BE为对角线时，‎ ‎∵B（5，0），E（1，8），‎ ‎∴线段BE的中点坐标为（3，4），则线段PQ的中点坐标为（3，4），‎ 设Q（x，y），且P（2，t），‎ ‎∴x+2=3×2，解得x=4，把x=4代入抛物线解析式可求得y=5，‎ ‎∴Q（4，5）；‎ 综上可知Q点的坐标为（﹣2，﹣7）或（6，﹣7）或（4，5）．‎ ‎6．（2017•贵阳）我们知道，经过原点的抛物线可以用y=ax2+bx（a≠0）表示，对于这样的抛物线：‎ ‎（1）当抛物线经过点（﹣2，0）和（﹣1，3）时，求抛物线的表达式；‎ ‎（2）当抛物线的顶点在直线y=﹣2x上时，求b的值；‎ ‎（3）如图，现有一组这样的抛物线，它们的顶点A1、A2、…，An在直线y=﹣2x上，横坐标依次为﹣1，﹣2，﹣3，…，﹣n（n为正整数，且n≤12），分别过每个顶点作x轴的垂线，垂足记为B1、B2，…，Bn，以线段AnBn为边向左作正方形AnBnCnDn，如果这组抛物线中的某一条经过点Dn，求此时满足条件的正方形AnBnCnDn的边长．‎ ‎【解答】解：（1）∵抛物线y=ax2+bx经过点（﹣2，0）和（﹣1，3），‎ ‎∴，解得，‎ ‎∴抛物线的表达式为y=﹣3x2﹣6x；‎ ‎（2）∵抛物线y=ax2+bx的顶点坐标是（﹣，﹣），且该点在直线y=﹣2x上，‎ ‎∴﹣=﹣2×（﹣），‎ ‎∵a≠0，∴﹣b2=4b，‎ 解得b1=﹣4，b2=0；‎ ‎（3）这组抛物线的顶点A1、A2、…，An在直线y=﹣2x上，‎ 由（2）可知，b=4或b=0．‎ ‎①当b=0时，抛物线的顶点在坐标原点，不合题意，舍去；‎ ‎②当b=﹣4时，抛物线的表达式为y=ax2﹣4x．‎ 由题意可知，第n条抛物线的顶点为An（﹣n，2n），则Dn（﹣3n，2n），‎ ‎∵以An为顶点的抛物线不可能经过点Dn，设第n+k（k为正整数）条抛物线经过点Dn，此时第n+k条抛物线的顶点坐标是An+k（﹣n﹣k，2n+2k），‎ ‎∴﹣=﹣n﹣k，∴a==﹣，‎ ‎∴第n+k条抛物线的表达式为y=﹣x2﹣4x，‎ ‎∵Dn（﹣3n，2n）在第n+k条抛物线上，‎ ‎∴2n=﹣×（﹣3n）2﹣4×（﹣3n），解得k=n，‎ ‎∵n，k为正整数，且n≤12，‎ ‎∴n1=5，n2=10．‎ 当n=5时，k=4，n+k=9；‎ 当n=10时，k=8，n+k=18＞12（舍去），‎ ‎∴D5（﹣15，10），‎ ‎∴正方形的边长是10．‎ ‎7．（2017•毕节市）如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；‎ ‎（3）动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．‎ ‎【解答】解：‎ ‎（1）设抛物线解析式为y=ax2+bx+c，‎ 把A、B、C三点坐标代入可得，解得，‎ ‎∴抛物线解析式为y=x2﹣3x﹣4；‎ ‎（2）作OC的垂直平分线DP，交OC于点D，交BC下方抛物线于点P，如图1，‎ ‎∴PO=PD，此时P点即为满足条件的点，‎ ‎∵C（0，﹣4），‎ ‎∴D（0，﹣2），‎ ‎∴P点纵坐标为﹣2，‎ 代入抛物线解析式可得x2﹣3x﹣4=﹣2，解得x=（小于0，舍去）或x=，‎ ‎∴存在满足条件的P点，其坐标为（，﹣2）；‎ ‎（3）∵点P在抛物线上，‎ ‎∴可设P（t，t2﹣3t﹣4），‎ 过P作PE⊥x轴于点E，交直线BC于点F，如图2，‎ ‎∵B（4，0），C（0，﹣4），‎ ‎∴直线BC解析式为y=x﹣4，‎ ‎∴F（t，t﹣4），‎ ‎∴PF=（t﹣4）﹣（t2﹣3t﹣4）=﹣t2+4t，‎ ‎∴S△PBC=S△PFC+S△PFB=PF•OE+PF•BE=PF•（OE+BE）=PF•OB=（﹣t2+4t）×4=﹣2（t﹣2）2+8，‎ ‎∴当t=2时，S△PBC最大值为8，此时t2﹣3t﹣4=﹣6，‎ ‎∴当P点坐标为（2，﹣6）时，△PBC的最大面积为8．‎ ‎8．（2017•西宁）如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）猜想△EDB的形状并加以证明；‎ ‎（3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．‎ ‎【解答】解：‎ ‎（1）在矩形OABC中，OA=4，OC=3，‎ ‎∴A（4，0），C（0，3），‎ ‎∵抛物线经过O、A两点，‎ ‎∴抛物线顶点坐标为（2，3），‎ ‎∴可设抛物线解析式为y=a（x﹣2）2+3，‎ 把A点坐标代入可得0=a（4﹣2）2+3，解得a=﹣，‎ ‎∴抛物线解析式为y=﹣（x﹣2）2+3，即y=﹣x2+3x；‎ ‎（2）△EDB为等腰直角三角形．‎ 证明：‎ 由（1）可知B（4，3），且D（3，0），E（0，1），‎ ‎∴DE2=32+12=10，BD2=（4﹣3）2+32=10，BE2=42+（3﹣1）2=20，‎ ‎∴DE2+BD2=BE2，且DE=BD，‎ ‎∴△EDB为等腰直角三角形；‎ ‎（3）存在．理由如下：‎ 设直线BE解析式为y=kx+b，‎ 把B、E坐标代入可得，解得，‎ ‎∴直线BE解析式为y=x+1，‎ 当x=2时，y=2，‎ ‎∴F（2，2），‎ ‎①‎ 当AF为平行四边形的一边时，则M到x轴的距离与F到x轴的距离相等，即M到x轴的距离为2，‎ ‎∴点M的纵坐标为2或﹣2，‎ 在y=﹣x2+3x中，令y=2可得2=﹣x2+3x，解得x=，‎ ‎∵点M在抛物线对称轴右侧，‎ ‎∴x＞2，‎ ‎∴x=，‎ ‎∴M点坐标为（，2）；‎ 在y=﹣x2+3x中，令y=﹣2可得﹣2=﹣x2+3x，解得x=，‎ ‎∵点M在抛物线对称轴右侧，‎ ‎∴x＞2，‎ ‎∴x=，‎ ‎∴M点坐标为（，﹣2）；‎ ‎②当AF为平行四边形的对角线时，‎ ‎∵A（4，0），F（2，2），‎ ‎∴线段AF的中点为（3，1），即平行四边形的对称中心为（3，1），‎ 设M（t，﹣t2+3t），N（x，0），‎ 则﹣t2+3t=2，解得t=，‎ ‎∵点M在抛物线对称轴右侧，‎ ‎∴x＞2，‎ ‎∴t=，‎ ‎∴M点坐标为（，2）；‎ 综上可知存在满足条件的点M，其坐标为（，2）或（，﹣2）．‎ ‎9．（2017•盐城）如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=﹣x2+bx+c经过A、C两点，与x轴的另一交点为点B．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）点D为直线AC上方抛物线上一动点；‎ ‎①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；‎ ‎②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）根据题意得A（﹣4，0），C（0，2），‎ ‎∵抛物线y=﹣x2+bx+c经过A、C两点，‎ ‎∴，‎ ‎∴，‎ ‎∴y=﹣x2﹣x+2；‎ ‎（2）①如图，令y=0，‎ ‎∴﹣x2﹣x+2=0，‎ ‎∴x1=﹣4，x2=1，‎ ‎∴B（1，0），‎ 过D作DM⊥x轴交AC于点M，过B作BN⊥x轴交于AC于N，‎ ‎∴DM∥BN，‎ ‎∴△DME∽△BNE，‎ ‎∴==，‎ 设D（a，﹣a2﹣a+2），‎ ‎∴M（a，a+2），‎ ‎∵B（1，0），‎ ‎∴N（1，），‎ ‎∴==（a+2）2+；‎ ‎∴当a=﹣2时，的最大值是；‎ ‎②∵A（﹣4，0），B（1，0），C（0，2），‎ ‎∴AC=2，BC=，AB=5，‎ ‎∴AC2+BC2=AB2，‎ ‎∴△ABC是以∠ACB为直角的直角三角形，取AB的中点P，‎ ‎∴P（﹣，0），‎ ‎∴PA=PC=PB=，‎ ‎∴∠CPO=2∠BAC，‎ ‎∴tan∠CPO=tan（2∠BAC）=，‎ 过D作x轴的平行线交y轴于R，交AC的延长线于G，‎ 情况一：如图，∴∠DCF=2∠BAC=∠DGC+∠CDG，‎ ‎∴∠CDG=∠BAC，‎ ‎∴tan∠CDG=tan∠BAC=，‎ 即，‎ 令D（a，﹣a2﹣a+2），‎ ‎∴DR=﹣a，RC=﹣a2﹣a，‎ ‎∴，‎ ‎∴a1=0（舍去），a2=﹣2，‎ ‎∴xD=﹣2，‎ 情况二，∴∠FDC=2∠BAC，‎ ‎∴tan∠FDC=，‎ 设FC=4k，‎ ‎∴DF=3k，DC=5k，‎ ‎∵tan∠DGC==，‎ ‎∴FG=6k，‎ ‎∴CG=2k，DG=3k，‎ ‎∴RC=k，RG=k，‎ DR=3k﹣k=k，‎ ‎∴==，‎ ‎∴a1=0（舍去），a2=﹣，‎ 点D的横坐标为﹣2或﹣．‎ ‎10．（2017•株洲）已知二次函数y=﹣x2+bx+c+1，‎ ‎①当b=1时，求这个二次函数的对称轴的方程； ‎ ‎②若c=﹣b2﹣2b，问：b为何值时，二次函数的图象与x轴相切？‎ ‎③若二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜x2，与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足=，求二次函数的表达式．‎ ‎【解答】解：①二次函数y=﹣x2+bx+c+1的对称轴为x=，‎ 当b=1时，=，‎ ‎∴当b=1时，求这个二次函数的对称轴的方程为x=．‎ ‎②二次函数y=﹣x2+bx+c+1的顶点坐标为（，），‎ ‎∵二次函数的图象与x轴相切且c=﹣b2﹣2b，‎ ‎∴，解得：b=，‎ ‎∴b为，二次函数的图象与x轴相切．‎ ‎③∵AB是半圆的直径，‎ ‎∴∠AMB=90°，‎ ‎∴∠OAM+∠OBM=90°，‎ ‎∵∠AOM=∠MOB=90°，‎ ‎∴∠OAM+∠OMA=90°，‎ ‎∴∠OMA=∠OBM，‎ ‎∴△OAM∽△OMB，‎ ‎∴，‎ ‎∴OM2=OA•OB，‎ ‎∵二次函数的图象与x轴交于点A（x1，0），B（x2，0），‎ ‎∴OA=﹣x1，OB=x2，x1+x2，=b，x1•x2=﹣（c+1），‎ ‎∵OM=c+1，‎ ‎∴（c+1）2=c+1，‎ 解得：c=0或c=﹣1（舍去），‎ ‎∴c=0，OM=1，‎ ‎∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足=，‎ ‎∴AD=BD，DF=4DE，‎ DF∥OM，‎ ‎∴△BDE∽△BOM，△AOM∽△ADF，‎ ‎∴，，‎ ‎∴DE=，DF=，‎ ‎∴×4，‎ ‎∴OB=4OA，即x2=﹣4x1，‎ ‎∵x1•x2=﹣（c+1）=﹣1，‎ ‎∴，解得：，‎ ‎∴b=﹣+2=，‎ ‎∴二次函数的表达式为y=﹣x2+x+1．‎ ‎11．（2017•枣庄）如图，抛物线y=﹣x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．‎ ‎（1）求抛物线的解析式及点D的坐标；‎ ‎（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；‎ ‎（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在坐标平面内，以线段MN为对角线作正方形MPNQ，请写出点Q的坐标．‎ ‎【解答】解：‎ ‎（1）把B、C两点坐标代入抛物线解析式可得，解得，‎ ‎∴抛物线解析式为y=﹣x2+2x+6，‎ ‎∵y=﹣x2+2x+6=﹣（x﹣2）2+8，‎ ‎∴D（2，8）；‎ ‎（2）如图1，过F作FG⊥x轴于点G，‎ 设F（x，﹣x2+2x+6），则FG=|﹣x2+2x+6|，‎ ‎∵∠FBA=∠BDE，∠FGB=∠BED=90°，‎ ‎∴△FBG∽△BDE，‎ ‎∴=，‎ ‎∵B（6，0），D（2，8），‎ ‎∴E（2，0），BE=4，DE=8，OB=6，‎ ‎∴BG=6﹣x，‎ ‎∴=，‎ 当点F在x轴上方时，有=，解得x=﹣1或x=6（舍去），此时F点的坐标为（﹣1，）；‎ 当点F在x轴下方时，有=﹣，解得x=﹣3或x=6（舍去），此时F点的坐标为（﹣3，﹣）；‎ 综上可知F点的坐标为（﹣1，）或（﹣3，﹣）；‎ ‎（3）如图2，设对角线MN、PQ交于点O′，‎ ‎∵点M、N关于抛物线对称轴对称，且四边形MPNQ为正方形，‎ ‎∴点P为抛物线对称轴与x轴的交点，点Q在抛物线的对称轴上，‎ 设Q（2，2n），则M坐标为（2﹣n，n），‎ ‎∵点M在抛物线y=﹣x2+2x+6的图象上，‎ ‎∴n=﹣（2﹣n）2+2（2﹣n）+6，解得n=﹣1+或n=﹣1﹣，‎ ‎∴满足条件的点Q有两个，其坐标分别为（2，﹣2+2）或（2，﹣2﹣2）．‎ ‎12．（2017•海南）抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0）．‎ ‎（1）求该抛物线所对应的函数解析式；‎ ‎（2）该抛物线与直线y=x+3相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．‎ ‎①连结PC、PD，如图1，在点P运动过程中，△‎ PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；‎ ‎②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．‎ ‎【解答】解：‎ ‎（1）∵抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0），‎ ‎∴，解得，‎ ‎∴该抛物线对应的函数解析式为y=x2﹣x+3；‎ ‎（2）①∵点P是抛物线上的动点且位于x轴下方，‎ ‎∴可设P（t，t2﹣t+3）（1＜t＜5），‎ ‎∵直线PM∥y轴，分别与x轴和直线CD交于点M、N，‎ ‎∴M（t，0），N（t，t+3），‎ ‎∴PN=t+3﹣（t2﹣t+3）=﹣（t﹣）2+‎ 联立直线CD与抛物线解析式可得，解得或，‎ ‎∴C（0，3），D（7，），‎ 分别过C、D作直线PN的直线，垂足分别为E、F，如图1，‎ 则CE=t，DF=7﹣t，‎ ‎∴S△PCD=S△PCN+S△PDN=PN•CE+PN•DF=PN=[﹣（t﹣）2+]=﹣（t﹣）2+，‎ ‎∴当t=时，△PCD的面积有最大值，最大值为；‎ ‎②存在．‎ ‎∵∠CQN=∠PMB=90°，‎ ‎∴当△CNQ与△PBM相似时，有或=两种情况，‎ ‎∵CQ⊥PM，垂足为Q，‎ ‎∴Q（t，3），且C（0，3），N（t，t+3），‎ ‎∴CQ=t，NQ=t+3﹣3=t，‎ ‎∴=，‎ ‎∵P（t，t2﹣t+3），M（t，0），B（5，0），‎ ‎∴BM=5﹣t，PM=0﹣（t2﹣t+3）=﹣t2+t﹣3，‎ 当时，则PM=BM，即﹣t2+t﹣3=（5﹣t），解得t=2或t=5（舍去），此时P（2，﹣）；‎ 当=时，则BM=PM，即5﹣t=（﹣t2+t﹣3），解得t=或t=5（舍去），此时P（，﹣）；‎ 综上可知存在满足条件的点P，其坐标为（2，﹣）或（，﹣）．‎ ‎　‎ ‎13．（2017•内江）如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；‎ ‎（3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．‎ ‎【解答】解：（1）∵点B坐标为（4，0），抛物线的对称轴方程为x=1．‎ ‎∴A（﹣2，0），‎ 把点A（﹣2，0）、B（4，0）、点C（0，3），分别代入y=ax2+bx+c（a≠0），得 ‎，‎ 解得 ，‎ 所以该抛物线的解析式为：y=﹣x2+x+3；‎ ‎（2）设运动时间为t秒，则AM=3t，BN=t．‎ ‎∴MB=6﹣3t．‎ 由题意得，点C的坐标为（0，3）．‎ 在Rt△BOC中，BC==5．‎ 如图1，过点N作NH⊥AB于点H．‎ ‎∴NH∥CO，‎ ‎∴△BHN∽△BOC，‎ ‎∴，即=，‎ ‎∴HN=t．‎ ‎∴S△MBN=MB•HN=（6﹣3t）•t=﹣t2+t=﹣（t﹣1）2+，‎ 当△PBQ存在时，0＜t＜2，‎ ‎∴当t=1时，‎ S△PBQ最大=．‎ 答：运动1秒使△PBQ的面积最大，最大面积是；‎ ‎（3）如图2，‎ 在Rt△OBC中，cos∠B==．‎ 设运动时间为t秒，则AM=3t，BN=t．‎ ‎∴MB=6﹣3t．‎ 当∠MNB=90°时，cos∠B==，即=，‎ 化简，得17t=24，解得t=，‎ 当∠BMN=90°时，cos∠B==，‎ 化简，得19t=30，解得t=，‎ 综上所述：t=或t=时，△MBN为直角三角形．‎ ‎14．（2017•广元）如图，已知抛物线y=ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．‎ ‎（1）求抛物线的解析式；‎ ‎（2）设点M（1，m），当MB+MD的值最小时，求m的值；‎ ‎（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；‎ ‎（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．‎ ‎【解答】解：（1）将A，B，C点的坐标代入解析式，得 ‎，‎ 解得，‎ 抛物线的解析式为y=﹣x2﹣2x+3‎ ‎（2）配方，得y=﹣（x+1）2+4，顶点D的坐标为（﹣1，4）‎ 作B点关于直线x=1的对称点B′，如图1，‎ 则B′（4，3），由（1）得D（﹣1，4），‎ 可求出直线DB′的函数关系式为y=﹣x+，‎ 当M（1，m）在直线DN′上时，MN+MD的值最小，‎ 则m=﹣×1+=．‎ ‎（3）作PE⊥x轴交AC于E点，如图2，‎ AC的解析式为y=x+3，设P（m，﹣m2﹣2m+3），E（m，m+3），‎ PE=﹣m2﹣2m+3﹣（m+3）=﹣m2﹣3m S△APC=PE•|xA|=（﹣m2﹣3m）×3=﹣（m+）2+，‎ 当m=﹣时，△APC的面积的最大值是；‎ ‎（4）由（1）、（2）得D（﹣1，4），N（﹣1，2）‎ 点E在直线AC上，设E（x，x+3），‎ ‎①当点E在线段AC上时，点F在点E上方，则F（x，﹣x2﹣2x+3），‎ ‎∵EF=DN ‎∴﹣x2﹣2x+3﹣（x+3）=4﹣2=2，‎ 解得，x=﹣2或x=﹣1（舍去），‎ 则点E的坐标为：（﹣2，1）．‎ ‎②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，﹣x2﹣2x+3），‎ ‎∵EF=DN，‎ ‎∴（x+3）﹣（﹣x2﹣2x+3）=2，‎ 解得x=或x=，‎ 即点E的坐标为：（，）或（，）‎ 综上可得满足条件的点E为E（﹣2，1）或：（，）或（，）．‎ ‎15．（2017•泸州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象经过A（﹣1，0）、B（4，0）、C（0，2）三点．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；‎ ‎（3）点P是该二次函数图象上位于第一象限上的一动点，连接PA分别交BC、y轴于点E、F，若△PEB、△CEF的面积分别为S1、S2，求S1﹣S2的最大值．‎ ‎【解答】解：‎ ‎（1）由题意可得，解得，‎ ‎∴抛物线解析式为y=﹣x2+x+2；‎ ‎（2）当点D在x轴上方时，过C作CD∥AB交抛物线于点D，如图1，‎ ‎∵A、B关于对称轴对称，C、D关于对称轴对称，‎ ‎∴四边形ABDC为等腰梯形，‎ ‎∴∠CAO=∠DBA，即点D满足条件，‎ ‎∴D（3，2）；‎ 当点D在x轴下方时，‎ ‎∵∠DBA=∠CAO，‎ ‎∴BD∥AC，‎ ‎∵C（0，2），‎ ‎∴可设直线AC解析式为y=kx+2，把A（﹣1，0）代入可求得k=2，‎ ‎∴直线AC解析式为y=2x+2，‎ ‎∴可设直线BD解析式为y=2x+m，把B（4，0）代入可求得m=﹣8，‎ ‎∴直线BD解析式为y=2x﹣8，‎ 联立直线BD和抛物线解析式可得，解得或，‎ ‎∴D（﹣5，﹣18）；‎ 综上可知满足条件的点D的坐标为（3，2）或（﹣5，﹣18）；‎ ‎（3）过点P作PH∥y轴交直线BC于点H，如图2，‎ 设P（t，﹣t2+t+2），‎ 由B、C两点的坐标可求得直线BC的解析式为y=﹣x+2，‎ ‎∴H（t，﹣t+2），‎ ‎∴PH=yP﹣yH=﹣t2+t+2﹣（﹣t+2）=﹣t2+2t，‎ 设直线AP的解析式为y=px+q，‎ ‎∴，解得，‎ ‎∴直线AP的解析式为y=（﹣t+2）（x+1），令x=0可得y=2﹣t，‎ ‎∴F（0，2﹣t），‎ ‎∴CF=2﹣（2﹣t）=t，‎ 联立直线AP和直线BC解析式可得，解得x=，即E点的横坐标为，‎ ‎∴S1=PH（xB﹣xE）=（﹣t2+2t）（4﹣），S2=••，‎ ‎∴S1﹣S2=（﹣t2+2t）（4﹣）﹣••=﹣t2+4t=﹣（t﹣）2+，‎ ‎∴当t=时，有S1﹣S2有最大值，最大值为．‎ ‎16．（2017•锦州）如图，抛物线y=x2+bx+‎ c经过B（﹣1，0），D（﹣2，5）两点，与x轴另一交点为A，点H是线段AB上一动点，过点H的直线PQ⊥x轴，分别交直线AD、抛物线于点Q，P．‎ ‎（1）求抛物线的解析式；‎ ‎（2）是否存在点P，使∠APB=90°，若存在，求出点P的横坐标，若不存在，说明理由；‎ ‎（3）连接BQ，一动点M从点B出发，沿线段BQ以每秒1个单位的速度运动到Q，再沿线段QD以每秒个单位的速度运动到D后停止，当点Q的坐标是多少时，点M在整个运动过程中用时t最少？‎ ‎【解答】解：（1）把B（﹣1，0），D（﹣2，5）代入y=x2+bx+c，‎ 得，解得，‎ ‎∴抛物线的解析式为：y=x2﹣2x﹣3；‎ ‎（2）存在点P，使∠APB=90°．‎ 当y=0时，即x2﹣2x﹣3=0，解得：x1=﹣1，x2=3，‎ ‎∴OB=1，OA=3．‎ 设P（m，m2﹣2m﹣3），则﹣1≤m≤3，PH=﹣（m2﹣2m﹣3），BH=1+m，AH=3﹣m，‎ ‎∵∠APB=90°，PH⊥AB，‎ ‎∴∠PAH=∠BPH=90°﹣∠APH，∠AHP=∠PHB，‎ ‎∴△AHP∽△PHB，‎ ‎∴=，‎ ‎∴PH2=BH•AH，‎ ‎∴[﹣（m2﹣2m﹣3）]2=（1+m）（3﹣m），‎ 解得m1=1+，m2=1﹣，‎ ‎∴点P的横坐标为：1+或1﹣；‎ ‎（3）如图，过点D作DN⊥x轴于点N，则DN=5，ON=2，AN=3+2=5，‎ ‎∴tan∠DAB===1，‎ ‎∴∠DAB=45°．‎ 过点D作DK∥x轴，则∠KDQ=∠DAB=45°，DQ=QG．‎ 由题意，动点M运动的路径为折线BQ+QD，运动时间：t=BQ+DQ，‎ ‎∴t=BQ+QG，即运动的时间值等于折线BQ+QG的长度值．‎ 由垂线段最短可知，折线BQ+QG的长度的最小值为DK与x轴之间的垂线段．‎ 过点B作BH⊥DK于点H，则t最小=BH，BH与直线AD的交点，即为所求之Q点．‎ ‎∵A（3，0），D（﹣2，5），‎ ‎∴直线AD的解析式为：y=﹣x+3，‎ ‎∵B点横坐标为﹣1，‎ ‎∴y=1+3=4，‎ ‎∴Q（﹣1，4）．‎ ‎17．（2017•乐山）如图1，抛物线C1：y=x2+ax与C2：y=﹣x2+bx相交于点O、C，C1与C2分别交x轴于点B、A，且B为线段AO的中点．‎ ‎（1）求 的值；‎ ‎（2）若OC⊥AC，求△OAC的面积；‎ ‎（3）抛物线C2的对称轴为l，顶点为M，在（2）的条件下：‎ ‎①点P为抛物线C2对称轴l上一动点，当△PAC的周长最小时，求点P的坐标；‎ ‎②如图2，点E在抛物线C2上点O与点M之间运动，四边形OBCE的面积是否存在最大值？若存在，求出面积的最大值和点E的坐标；若不存在，请说明理由．‎ ‎【解答】解：‎ ‎（1）在y=x2+ax中，当y=0时，x2+ax=0，x1=0，x2=﹣a，‎ ‎∴B（﹣a，0），‎ 在y=﹣x2+bx中，当y=0时，﹣x2+bx=0，x1=0，x2=b，‎ ‎∴A（0，b），‎ ‎∵B为OA的中点，‎ ‎∴b=﹣2a，‎ ‎∴；‎ ‎（2）联立两抛物线解析式可得，消去y整理可得2x2+3ax=0，解得x1=0，，‎ 当时，，‎ ‎∴，‎ 过C作CD⊥x轴于点D，如图1，‎ ‎∴，‎ ‎∵∠OCA=90°，‎ ‎∴△OCD∽△CAD，‎ ‎∴，‎ ‎∴CD2=AD•OD，即，‎ ‎∴a1=0（舍去），（舍去），，‎ ‎∴，，‎ ‎∴；‎ ‎（3）①抛物线，‎ ‎∴其对称轴，‎ 点A关于l2的对称点为O（0，0），，‎ 则P为直线OC与l2的交点，‎ 设OC的解析式为y=kx，‎ ‎∴，得，‎ ‎∴OC的解析式为，‎ 当时，，‎ ‎∴；‎ ‎②设，‎ 则，‎ 而，，‎ 设直线BC的解析式为y=kx+b，‎ 由，解得，‎ ‎∴直线BC的解析式为，‎ 过点E作x轴的平行线交直线BC于点N，如图2，‎ 则，即x=，‎ ‎∴EN=，‎ ‎∴‎ ‎∴S四边形OBCE=S△OBE+S△EBC==，‎ ‎∵，‎ ‎∴当时，，‎ 当时，，‎ ‎∴，．‎ ‎18．（2017•黔南州）如图，已知直角坐标系中，A、B、D三点的坐标分别为A（8，0），B（0，4），D（﹣1，0），点C与点B关于x轴对称，连接AB、AC．‎ ‎（1）求过A、B、D三点的抛物线的解析式；‎ ‎（2）有一动点E从原点O出发，以每秒2个单位的速度向右运动，过点E作x轴的垂线，交抛物线于点P，交线段CA于点M，连接PA、PB，设点E运动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S与t的函数关系式，并求出四边形PBCA的最大面积；‎ ‎（3）抛物线的对称轴上是否存在一点H，使得△ABH是直角三角形？若存在，请直接写出点H的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）∵A（8，0），D（﹣1，0），‎ 设过A、B、D三点的抛物线的解析式为y=a（x+1）（x﹣8），将B（0，4）代入得﹣8a=4，‎ ‎∴a=﹣，‎ ‎∴抛物线的解析式为y=﹣（x+1）（x﹣8）=﹣x2+x+4；‎ ‎（2）△ABC中，AB=AC，AO⊥BC，则OB=OC=4，‎ ‎∴C（0，﹣4）．‎ 由A（8，0）、B（0，4），得：直线AB：y=﹣x+4；‎ 依题意，知：OE=2t，即 E（2t，0）；‎ ‎∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；‎ S=S△ABC+S△PAB=×8×8+×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；‎ ‎∴当t=2时，S有最大值，且最大值为64；‎ ‎（3）存在，‎ ‎∵抛物线的对称轴为：x==，‎ ‎∴设H（，m），‎ ‎∵A（8，0），B（0，4），‎ ‎∴AH2=（8﹣）2+m2=+m2，AB2=82+42=80，BH2=（）2+（4﹣m）2=m2﹣8m+①当∠ABH=90°时，AH2=BH2+AB2，即+m2=m2﹣8m++80，‎ 解得：m=11，‎ ‎∴H（，11），‎ ‎②当∠AHB=90°时，AH2+BH2=AB2，+m2+m2﹣8m+=80，‎ 解得：m=2±，‎ ‎∴H（，2+），（，2﹣），‎ ‎③当∠BAH=90°时，AB2+AH2=HB2，即80++m2=m2﹣8m+，‎ 解得：m=﹣9，‎ ‎∴H（，﹣9），‎ 综上所述，H（，11）或（，2+）或（，2﹣）或（，﹣9）．‎ ‎19．（2017•怀化）如图1，在平面直角坐标系中，已知抛物线y=ax2+bx﹣5与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标；‎ ‎（3）如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；‎ ‎（4）若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．‎ ‎【解答】解：（1）∵点A（﹣1，0），B（5，0）在抛物线y=ax2+bx﹣5上，‎ ‎∴，‎ ‎∴，‎ ‎∴抛物线的表达式为y=x2﹣4x﹣5，‎ ‎（2）如图1，令x=0，则y=﹣5，‎ ‎∴C（0，﹣5），‎ ‎∴OC=OB，‎ ‎∴∠OBC=∠OCB=45°，‎ ‎∴AB=6，BC=5，‎ 要使以B，C，D为顶点的三角形与△ABC相似，则有或，‎ ‎①当时，‎ CD=AB=6，‎ ‎∴D（0，1），‎ ‎②当时，‎ ‎∴，‎ ‎∴CD=，‎ ‎∴D（0，），‎ 即：D的坐标为（0，1）或（0，）；‎ ‎（3）设H（t，t2﹣4t﹣5），‎ ‎∵CE∥x轴，‎ ‎∴点E的纵坐标为﹣5，‎ ‎∵E在抛物线上，‎ ‎∴x2﹣4x﹣5=﹣5，‎ ‎∴x=0（舍）或x=4，‎ ‎∴E（4，﹣5），‎ ‎∴CE=4，‎ ‎∵B（5，0），C（0，﹣5），‎ ‎∴直线BC的解析式为y=x﹣5，‎ ‎∴F（t，t﹣5），‎ ‎∴HF=t﹣5﹣（t2﹣4t﹣5）=﹣（t﹣）2+，‎ ‎∵CE∥x轴，HF∥y轴，‎ ‎∴CE⊥HF，‎ ‎∴S四边形CHEF=CE•HF=﹣2（t﹣）2+，‎ 当t=时，四边形CHEF的面积最大为．‎ 当t=时，t2﹣4t﹣5=﹣10﹣5=﹣，‎ ‎∴H（，﹣）；‎ ‎（4）如图2，∵K为抛物线的顶点，‎ ‎∴K（2，﹣9），‎ ‎∴K关于y轴的对称点K'（﹣2，﹣9），‎ ‎∵M（4，m）在抛物线上，‎ ‎∴M（4，﹣5），‎ ‎∴点M关于x轴的对称点M'（4，5），‎ ‎∴直线K'M'的解析式为y=x﹣，‎ ‎∴P（，0），Q（0，﹣）．‎ ‎20．（2017•绵阳）如图，已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2，1），并且经过点（4，2），直线y=x+1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C与直线m交于对称轴右侧的点M（t，1），直线m上每一点的纵坐标都等于1．‎ ‎（1）求抛物线的解析式；‎ ‎（2）证明：圆C与x轴相切；‎ ‎（3）过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F，求BE：MF的值．‎ ‎【解答】解：‎ ‎（1）∵已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2，1），‎ ‎∴可设抛物线解析式为y=a（x﹣2）2+1，‎ ‎∵抛物线经过点（4，2），‎ ‎∴2=a（4﹣2）2+1，解得a=，‎ ‎∴抛物线解析式为y=（x﹣2）2+1=x2﹣x+2；‎ ‎（2）联立直线和抛物线解析式可得，解得或，‎ ‎∴B（3﹣，﹣），D（3+，+），‎ ‎∵C为BD的中点，‎ ‎∴点C的纵坐标为=，‎ ‎∵BD==5，‎ ‎∴圆的半径为，‎ ‎∴点C到x轴的距离等于圆的半径，‎ ‎∴圆C与x轴相切；‎ ‎（3）如图，过点C作CH⊥m，垂足为H，连接CM，‎ 由（2）可知CM=，CH=﹣1=，‎ 在Rt△CMH中，由勾股定理可求得MH=2，‎ ‎∵HF==，‎ ‎∴MF=HF﹣MH=﹣2，‎ ‎∵BE=﹣﹣1=﹣，‎ ‎∴==．‎ ‎21．（2017•辽阳）如图1，抛物线y=x2+bx+c经过A（﹣2，0）、B（0，﹣2）两点，点C在y轴上，△ABC为等边三角形，点D从点A出发，沿AB方向以每秒2个单位长度的速度向终点B运动，设运动时间为t秒（t＞0），过点D作DE⊥AC于点E，以DE为边作矩形DEGF，使点F在x轴上，点G在AC或AC的延长线上．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将矩形DEGF沿GF所在直线翻折，得矩形D'E'GF，当点D的对称点D'落在抛物线上时，求此时点D'的坐标；‎ ‎（3）如图2，在x轴上有一点M（2‎ ‎，0），连接BM、CM，在点D的运动过程中，设矩形DEGF与四边形ABMC重叠部分的面积为S，直接写出S与t之间的函数关系式，并写出自变量t的取值范围．‎ ‎【解答】解：（1）把A（﹣2，0）、B（0，﹣2）代入抛物线的解析式得：，解得：，‎ ‎∴抛物线的解析式为y=x2+x﹣2．‎ ‎（2）A（﹣2，0）、B（0，﹣2），‎ ‎∴OA=2，OB=2．‎ ‎∵AD=2t，∠DEA=90°，∠BAC=60°，‎ ‎∴AE=t，DE=t．‎ ‎∵△ABC为等边三角形，‎ ‎∴∠BAC=60°．‎ ‎∵AO⊥BC，‎ ‎∴∠CAO=∠BAO=30°．‎ ‎∵四边形DEGF为矩形，‎ ‎∴DF∥AC，GF=DE=t．‎ ‎∴∠DFA=∠CAO=30°，‎ ‎∴AF=2GF=2t．‎ ‎∴∠DFA=∠BAO=30°．‎ ‎∴DF=AD=2t．‎ 过点D′作D′H⊥x轴与点H．‎ ‎∵∠D′FH=∠AFD=30°，‎ ‎∴D′H=D′F=t，FH=D′H=t．‎ ‎∴AH=AF+FH=3t．‎ ‎∴OH=AH﹣AO=3t﹣2．‎ ‎∴D′（3t﹣2，t）．‎ 把点D′（3t﹣2，t）代入y=x2+x﹣2得：t=（3t﹣2）2+（3t﹣2）﹣2．整理得：9t2﹣10t=0，‎ 解得t=或t=0（舍去）．‎ ‎∴D′（，）．‎ ‎（3）由（2）可知：DE=t，DF=2t，AE=t．‎ 如图2所示：当AE+EG≤AC时，即t+2t≤4，解得：t≤．‎ ‎∴当0＜t≤时，S=ED•DF=2t2．‎ 当＜t≤2时，如图3所示：‎ ‎∵CG=AG﹣AC，‎ ‎∴CG=3t﹣4，‎ ‎∴GN=3t﹣4．‎ ‎∴S=ED•DF﹣CG•GN=2t2﹣（3t﹣4）×（3t﹣4）=﹣t2+12t﹣8．‎ 综上所述，S与t的函数关系式为S=．‎ ‎22．（2017•贺州）如图，在平面直角坐标系中，△ABC为等腰直角三角形，∠ACB=90°，抛物线y=﹣x2+bx+c经过A，B两点，其中点A，C的坐标分别为（1，0），（﹣4，0），抛物线的顶点为点D．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点E是直角三角形ABC斜边AB上的一个动点（不与A，B重合），过点E作x轴的垂线，交抛物线于点F，当线段FE的长度最大时，求点E的坐标；‎ ‎（3）在（2）的条件下，抛物线上是否存在一点P，使△PEF是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）∵A，C的坐标分别为（1，0），（﹣4，0），‎ ‎∴AC=5．‎ ‎∵△ABC为等腰直角三角形，∠C=90°，‎ ‎∴BC=AC=5．‎ ‎∴B（﹣4，﹣5）．‎ 将点A和点B的坐标代入得：，解得：，‎ ‎∴抛物线的解析式为y=﹣x2﹣2x+3．‎ ‎（2）如图1所示：‎ 设直线AB的解析式为y=kx+b，将点A和点B的坐标代入得：，解得：k=1，b=﹣1．‎ 所以直线AB的解析式为y=x﹣1．‎ 设点E的坐标为（t，t﹣1），则点F的坐标为（t，﹣t2﹣2t+3）．‎ ‎∴EF=﹣t2﹣2t+3﹣（t﹣1）=﹣t2﹣3t+4=（t+）2+．‎ ‎∴当t=﹣时，FE取最大值，此时，点E的坐标为（﹣，﹣）．‎ ‎（3）存在点P，能使△PEF是以EF为直角边的直角三角形．‎ 理由：如图所示：过点F作直线a⊥EF，交抛物线于点P，过点E作直线b⊥EF，交抛物线P′、P″．‎ 由（2）可知点E的坐标为（t，t﹣1），则点F的坐标为（t，﹣t2﹣2t+3），t=﹣，‎ ‎∴点E（﹣，﹣）、F（﹣，）．‎ ‎①当﹣t2﹣2t+3=时，解得：x=﹣或x=﹣（舍去）．‎ ‎∴点P的坐标为（﹣，）．‎ ‎②当﹣t2﹣2t+3=﹣时，解得：x=﹣1+或x=﹣1﹣．‎ ‎∴点P′（﹣1﹣，﹣），P″（﹣1+，﹣）．‎ 综上所述，点P的坐标为（﹣，）或（﹣1﹣，﹣）或P″（﹣1+，﹣）．‎ ‎23．（2017•达州）如图1，点A坐标为（2，0），以OA为边在第一象限内作等边△OAB，点C为x轴上一动点，且在点A右侧，连接BC，以BC为边在第一象限内作等边△BCD，连接AD交BC于E．‎ ‎（1）①直接回答：△OBC与△ABD全等吗？‎ ‎②试说明：无论点C如何移动，AD始终与OB平行；‎ ‎（2）当点C运动到使AC2=AE•AD时，如图2，经过O、B、C三点的抛物线为y1．试问：y1上是否存在动点P，使△BEP为直角三角形且BE为直角边？若存在，求出点P坐标；若不存在，说明理由；‎ ‎（3）在（2）的条件下，将y1沿x轴翻折得y2，设y1与y2组成的图形为M，函数y=x+m的图象l与M有公共点．试写出：l与M的公共点为3个时，m的取值．‎ ‎【解答】解：（1）①△OBC与△ABD全等，‎ 理由是：如图1，∵△OAB和△BCD是等边三角形，‎ ‎∴∠OBA=∠CBD=60°，‎ OB=AB，BC=BD，‎ ‎∴∠OBA+∠ABC=∠CBD+∠ABC，‎ 即∠OBC=∠ABD，‎ ‎∴△OBC≌△ABD（SAS）；‎ ‎②∵△OBC≌△ABD，‎ ‎∴∠BAD=∠BOC=60°，‎ ‎∴∠OBA=∠BAD，‎ ‎∴OB∥AD，‎ ‎∴无论点C如何移动，AD始终与OB平行；‎ ‎（2）如图2，∵AC2=AE•AD，‎ ‎∴，‎ ‎∵∠EAC=∠DAC，‎ ‎∴△AEC∽△ACD，‎ ‎∴∠ECA=∠ADC，‎ ‎∵∠BAD=∠BAO=60°，‎ ‎∴∠DAC=60°，‎ ‎∵∠BED=∠AEC，‎ ‎∴∠ACB=∠ADB，‎ ‎∴∠ADB=∠ADC，‎ ‎∵BD=CD，‎ ‎∴DE⊥BC，‎ Rt△ABE中，∠BAE=60°，‎ ‎∴∠ABE=30°，‎ ‎∴AE=AB=×2=1，‎ Rt△AEC中，∠EAC=60°，‎ ‎∴∠ECA=30°，‎ ‎∴AC=2AE=2，‎ ‎∴C（4，0），‎ 等边△OAB中，过B作BH⊥x轴于H，‎ ‎∴BH==，‎ ‎∴B（1，），‎ 设y1的解析式为：y=ax（x﹣4），‎ 把B（1，）代入得：=a（1﹣4），‎ a=﹣，‎ ‎∴设y1的解析式为：y1=﹣x（x﹣4）=﹣x2+x，‎ 过E作EG⊥x轴于G，‎ Rt△AGE中，AE=1，‎ ‎∴AG=AE=，‎ EG==，‎ ‎∴E（，），‎ 设直线AE的解析式为：y=kx+b，‎ 把A（2，0）和E（，）代入得：，‎ 解得：，‎ ‎∴直线AE的解析式为：y=x﹣2，‎ 则，‎ 解得：，，‎ ‎∴P（3，）或（﹣2，﹣4）；‎ 由（2）知：OB∥AD，‎ ‎∴∠OBE=∠AEC=90°，‎ ‎∴△OBE是直角三角形，‎ ‎∴P在点O处时，也符合条件，‎ 综上所述，点P的坐标为：（3，）或（﹣2，﹣4）或（0，0）；‎ ‎（3）如图3，‎ y1=﹣x2+x=﹣（x﹣2）2+，‎ 顶点（2，），‎ ‎∴抛物线y2的顶点为（2，﹣），‎ ‎∴y2=（x﹣2）2﹣，‎ ‎∵直线y=x+m和组成图形M的抛物线y1有两个交点或一个交点或没有交点，‎ 抛物线y2有两个交点或一个交点或没有交点，‎ 要图象M和直线y=x+m只有3个交点，则直线y=x+m和y1或y2相切，‎ 当y2与l相切时，直线l与y2只有一个公共点，即：l与图形M有3个公共点，‎ 则，‎ ‎=﹣，‎ x2﹣7x﹣3m=0，‎ ‎△=（﹣7）2﹣4×1×（﹣3m）=0，‎ m=﹣，‎ 当y1与l相切时，直线l与y1只有一个公共点，l与图形M有3个公共点，‎ ‎∴，‎ ‎∴x2﹣x+3m=0，‎ ‎∴△=1﹣12m=0，‎ ‎∴m=，‎ 当直线经过（0，0）或（4，0）时，也符合题意，此时m=0或﹣4‎ ‎∴当l与M的公共点为3个时，m的取值是：m=﹣或m=或0或﹣4．‎ ‎24．（2017•葫芦岛）如图，抛物线y=ax2﹣2x+c（a≠0）与x轴、y轴分别交于点A，B，C三点，已知点A（﹣2，0），点C（0，﹣8），点D是抛物线的顶点．‎ ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）如图1，抛物线的对称轴与x轴交于点E，第四象限的抛物线上有一点P，将△EBP沿直线EP折叠，使点B的对应点B'落在抛物线的对称轴上，求点P的坐标；‎ ‎（3）如图2，设BC交抛物线的对称轴于点F，作直线CD，点M是直线CD上的动点，点N是平面内一点，当以点B，F，M，N为顶点的四边形是菱形时，请直接写出点M的坐标．‎ ‎【解答】解：（1）将点A、点C的坐标代入抛物线的解析式得：，‎ 解得：a=1，c=﹣8．‎ ‎∴抛物线的解析式为y=x2﹣2x﹣8．‎ ‎∵y=（x﹣1）2﹣9，‎ ‎∴D（1，﹣9）．‎ ‎（2）将y=0代入抛物线的解析式得：x2﹣2x﹣8=0，解得x=4或x=﹣2，‎ ‎∴B（4，0）．‎ ‎∵y=（x﹣1）2﹣9，‎ ‎∴抛物线的对称轴为x=1，‎ ‎∴E（1，0）．‎ ‎∵将△EBP沿直线EP折叠，使点B的对应点B'落在抛物线的对称轴上，‎ ‎∴EP为∠BEF的角平分线．‎ ‎∴∠BEP=45°．‎ 设直线EP的解析式为y=﹣x+b，将点E的坐标代入得：﹣1+b=0，解得b=1，‎ ‎∴直线EP的解析式为y=﹣x+1．‎ 将y=﹣x+1代入抛物线的解析式得：﹣x+1=x2﹣2x﹣8，解得：x=或x=．‎ ‎∵点P在第四象限，‎ ‎∴x=．‎ ‎∴y=．‎ ‎∴P（，）．‎ ‎（3）设CD的解析式为y=kx﹣8，将点D的坐标代入得：k﹣8=﹣9，解得k=﹣1，‎ ‎∴直线CD的解析式为y=﹣x﹣8．‎ 设直线CB的解析式为y=k2x﹣8，将点B的坐标代入得：4k2﹣8=0，解得：k2=2．‎ ‎∴直线BC的解析式为y=2x﹣8．‎ 将x=1代入直线BC的解析式得：y=﹣6，‎ ‎∴F（1，﹣6）．‎ 设点M的坐标为（a，﹣a﹣8）．‎ 当MF=MB时，（a﹣4）2+（a+8）2=（a﹣1）2+（a+2）2，整理得：6a=﹣75，解得：a=﹣．‎ ‎∴点M的坐标为（﹣，）．‎ 当FM=FB时，（a﹣1）2+（a+2）2=（4﹣1）2+（﹣6﹣0）2，整理得：a2+a﹣20=0，解得：a=4或a=﹣5．‎ ‎∴点M的坐标为（4，﹣12）或（﹣5，﹣3）．‎ 综上所述，点M的坐标为（﹣，）或（4，﹣12）或（﹣5，﹣3）．‎ ‎25．（2017•十堰）抛物线y=x2+bx+c与x轴交于A（1，0），B（m，0），与y轴交于C．‎ ‎（1）若m=﹣3，求抛物线的解析式，并写出抛物线的对称轴；‎ ‎（2）如图1，在（1）的条件下，设抛物线的对称轴交x轴于D，在对称轴左侧的抛物线上有一点E，使S△ACE=S△ACD，求点E的坐标；‎ ‎（3）如图2，设F（﹣1，﹣4），FG⊥y于G，在线段OG上是否存在点P，使∠OBP=∠FPG？若存在，求m的取值范围；若不存在，请说明理由．‎ ‎【解答】解：（1）当m=﹣3时，B（﹣3，0），‎ 把A（1，0），B（﹣3，0）代入到抛物线y=x2+bx+c中得：‎ ‎，解得，‎ ‎∴抛物线的解析式为：y=x2+2x﹣3=（x+1）2﹣4；‎ 对称轴是：直线x=﹣1；‎ ‎（2）如图1，设E（m，m2+2m﹣3），‎ 由题意得：AD=1+1=2，OC=3，‎ S△ACE=S△ACD=×AD•OC=×2×3=10，‎ 设直线AE的解析式为：y=kx+b，‎ 把A（1，0）和E（m，m2+2m﹣3）代入得，‎ ‎，‎ 解得：，‎ ‎∴直线AE的解析式为：y=（m+3）x﹣m﹣3，‎ ‎∴F（0，﹣m﹣3），‎ ‎∵C（0，﹣3），‎ ‎∴FC=﹣m﹣3+3=﹣m，‎ ‎∴S△ACE=FC•（1﹣m）=10，‎ ‎﹣m（1﹣m）=20，‎ m2﹣m﹣20=0，‎ ‎（m+4）（m﹣5）=0，‎ m1=﹣4，m2=5（舍），‎ ‎∴E（﹣4，5）；‎ ‎（3）设点P（0，y）．‎ ‎①当m＜0时，‎ 如图2，△POB∽△FGP 得=‎ ‎∴m=y2+4y=（y+2）2﹣4‎ ‎∵﹣4＜y＜0，‎ ‎∴﹣4≤m＜0．‎ ‎②当m＞0时，‎ 如图3，△POB∽△FGP ‎∴=‎ ‎∴=‎ ‎∴m=﹣y2﹣4y=﹣（y+2）2+4‎ ‎∴﹣4＜y＜0‎ ‎∴0＜m≤4‎ 综上所述，m的取值范围是﹣4≤m≤4且m≠0．‎ ‎　26．（2017•黔东南州）如图，⊙M的圆心M（﹣1，2），⊙M经过坐标原点O，与y轴交于点A．经过点A的一条直线l解析式为：y=﹣x+4与x轴交于点B，以M为顶点的抛物线经过x轴上点D（2，0）和点C（﹣4，0）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）求证：直线l是⊙M的切线；‎ ‎（3）点P为抛物线上一动点，且PE与直线l垂直，垂足为E；PF∥y轴，交直线l于点F，是否存在这样的点P，使△PEF的面积最小．若存在，请求出此时点P的坐标及△PEF面积的最小值；若不存在，请说明理由．‎ ‎【解答】解：（1）设抛物线的解析式为y=a（x﹣2）（x+4），将点M的坐标代入得：﹣9a=2，解得：a=﹣．‎ ‎∴抛物线的解析式为y=﹣x2﹣x+．‎ ‎（2）连接AM，过点M作MG⊥AD，垂足为G．‎ 把x=0代入y=﹣x+4得：y=4，‎ ‎∴A（0，4）．‎ 将y=0代入得：0=﹣x+4，解得x=8，‎ ‎∴B（8，0）．‎ ‎∴OA=4，OB=8．‎ ‎∵M（﹣1，2），A（0，4），‎ ‎∴MG=1，AG=2．‎ ‎∴tan∠MAG=tan∠ABO=．‎ ‎∴∠MAG=∠ABO．‎ ‎∵∠OAB+∠ABO=90°，‎ ‎∴∠MAG+∠OAB=90°，即∠MAB=90°．‎ ‎∴l是⊙M的切线．‎ ‎（3）∵∠PFE+∠FPE=90°，∠FBD+∠PFE=90°，‎ ‎∴∠FPE=∠FBD．‎ ‎∴tan∠FPE=．‎ ‎∴PF：PE：EF=：2：1．‎ ‎∴△PEF的面积=PE•EF=×PF•PF=PF2．‎ ‎∴当PF最小时，△PEF的面积最小．‎ 设点P的坐标为（x，﹣x2﹣x+），则F（x，﹣x+4）．‎ ‎∴PF=（﹣x+4）﹣（﹣x2﹣x+）=﹣x+4+x2+x﹣=x2﹣x+=（x﹣）2+．‎ ‎∴当x=时，PF有最小值，PF的最小值为．‎ ‎∴P（，）．‎ ‎∴△PEF的面积的最小值为=×（）2=．‎ ‎27．（2017•抚顺）如图，抛物线y=ax2+bx+4交y轴于点A，并经过B（4，4）和C（6，0）两点，点D的坐标为（4，0），连接AD，BC，点E从点A出发，以每秒个单位长度的速度沿线段AD向点D运动，到达点D后，以每秒1个单位长度的速度沿射线DC运动，设点E的运动时间为t秒，过点E作AB的垂线EF交直线AB于点F，以线段EF为斜边向右作等腰直角△EFG．‎ ‎（1）求抛物线的解析式；‎ ‎（2）当点G落在第一象限内的抛物线上时，求出t的值；‎ ‎（3）设点E从点A出发时，点E，F，G都与点A重合，点E在运动过程中，当△BCG的面积为4时，直接写出相应的t值，并直接写出点G从出发到此时所经 过的路径长．‎ ‎【解答】解：（1）将B（4，4）和C（6，0）代入抛物线y=ax2+bx+4得：‎ ‎，‎ 解得：，‎ ‎∴抛物线的解析式为：y=﹣x2+x+4；‎ ‎（2）如图1，由题意得：AE=t，‎ ‎∵A（0，4），B（4，4），‎ ‎∴AB⊥y轴，且AB∥x轴，‎ ‎∵OA=OD=4，‎ ‎∴△AOD是等腰直角三角形，‎ ‎∴∠ADO=∠BAD=45°，‎ ‎∴△AFE是等腰直角三角形，‎ ‎∴AF=EF=t，‎ ‎∵△EFG是等腰直角三角形，‎ ‎∴G（t+t，4﹣t），‎ 即：点G（，4﹣t），‎ 将点G（，4﹣t）代入到抛物线得：‎ ‎4﹣t=﹣（）2++4，‎ 解得：t1=0（舍），t2=，‎ 答：当t=时，点G落在抛物线上；‎ ‎（3）如图2，连接BD，当G在BD上时，‎ ‎=4，‎ t=，‎ ‎①当0≤t≤时，如图3，‎ 过G作GH⊥x轴于H，延长HG交AB于M，则GM⊥AB，‎ ‎∵B（4，4），D（4，0），‎ ‎∴BD⊥x轴，‎ ‎∴S△BCG=S梯形GHDB+S△BDC﹣S△GHC，‎ ‎4=（4﹣+4）（4﹣）+×4×（6﹣4）﹣（6﹣）（4﹣t），‎ ‎4=t，‎ 解得：t=，‎ ‎∴AM==×=，‎ GM=t=×=，‎ 在Rt△AGM中，由勾股定理得：AG===；‎ ‎∴当t=时，此时点G运动的路径长为；‎ ‎②当G在BC上时，如图4，‎ tan∠C==2，‎ ‎∴GH=2HC，‎ ‎∴4﹣t=2（6﹣），‎ t=，‎ 当＜t≤时，如图5，‎ S△BCG=S△BDC﹣S梯形BDHG﹣S△GHC，‎ ‎4=×4×2﹣（4﹣+4）（t﹣4）﹣×，‎ t=（不在此范围内，不符合题意），‎ ‎③当E与D重合时，F与B重合，如图6，‎ t==4，‎ ‎∴G（6，2），‎ ‎∴AG==2，‎ ‎∴S△BCG=S梯形BDCG﹣S△BDC=×2×（4+2）﹣×2×4=2，‎ ‎∴当t＞4时，如图7，‎ 由题意得：DE=t﹣4，‎ ‎∴OE=t﹣4+4=t，‎ ‎∴OH=OE+EH=t+2，‎ EH=2，GM=GH=2，‎ BM=t+2﹣4=t﹣2，‎ CH=t+2﹣6=t﹣4，‎ 过G作MH⊥x轴，交x轴于H，交直线AB于M，‎ ‎∴S△BGC=S梯形BCHM﹣S△BGM﹣S△GCH，‎ ‎4=（t﹣4+t﹣2）×4﹣×2×（t﹣2）﹣×2×（t﹣4），‎ t=5，‎ 当t=5时，点G的运动路径分为两部分组成：‎ i）点G从A运动到D时，运动路径为：如图6中的AG长，即为2；‎ ii）点G从D点继续在射线DC上运动1秒时，路径为1；‎ 所以当t=5时，此时点G运动的路径长度为1+2．‎ 综上所述：当t1=秒，此时路径长度为，‎ 当t2=5秒，此时路径长度为1+2．‎ ‎28．（2017•莱芜）抛物线y=ax2+bx+c过A（2，3），B（4，3），C（6，﹣5）三点．‎ ‎（1）求抛物线的表达式；‎ ‎（2）如图①，抛物线上一点D在线段AC的上方，DE⊥AB交AC于点E，若满足=‎ ‎，求点D的坐标；‎ ‎（3）如图②，F为抛物线顶点，过A作直线l⊥AB，若点P在直线l上运动，点Q在x轴上运动，是否存在这样的点P、Q，使得以B、P、Q为顶点的三角形与△ABF相似，若存在，求P、Q的坐标，并求此时△BPQ的面积；若不存在，请说明理由．‎ ‎【解答】解：（1）根据题意，设抛物线表达式为y=a（x﹣3）2+h．‎ 把B（4，3），C（6，﹣5）代入得：，‎ 解得：，‎ 故抛物线的表达式为：y=﹣（x﹣3）2+4=﹣x2+6x﹣5；‎ ‎（2）设直线AC的表达式为y=kx+n，‎ 则：，‎ 解得：k=﹣2，n=7，‎ ‎∴直线AC的表达式为y=﹣2x+7，‎ 设点D（m，﹣m+6m﹣5），2＜m＜6，则点E（m，﹣2m+7），‎ ‎∴DE=（﹣m2+6m﹣5）﹣（﹣2m+7）=﹣m2+8m﹣12，‎ 设直线DE与直线AB交于点G，‎ ‎∵AG⊥EG，‎ ‎∴AG=m﹣2，EG=3﹣（﹣2m+7）=2（m﹣2），‎ m﹣2＞0，‎ 在Rt△AEG中，‎ ‎∴AE=（m﹣2），‎ 由，得=，‎ 化简得，2m2﹣11m+14=0，‎ 解得：m1=，m2=2（舍去），‎ 则D（，）．‎ ‎（3）根据题意得：△ABF为等腰直角三角形，假设存在满足条件的点P、Q，则△BPQ为等腰直角三角形，‎ 分三种情况：‎ ‎①若∠BPQ=90°，BP=PQ，‎ 如图2，过P作MN∥x轴，过Q作QM⊥MN于M，过B作BN⊥MN于N，‎ 易证得：△BAP≌△QMP，‎ ‎∴AB=QM=2，PM=AP=3+2=5，‎ ‎∴P（2，﹣2），Q（﹣3，0），‎ 在Rt△QMP中，PM=5，QM=2，‎ 由勾股定理得：PQ==，‎ ‎∴S△BPQ=PQ•PB=；‎ 如图3，易证得：△BAP≌△PMQ，‎ ‎∴AB=PM=2，AP=MQ=3﹣2=1，‎ ‎∴P（2，2），Q（3，0），‎ 在Rt△QMP中，PM=2，QM=1，‎ 由勾股定理得：PQ=，‎ ‎∴S△BPQ=PQ•PB=；‎ ‎②若∠BQP=90°，BQ=PQ，‎ 如图4，易得：△BNQ≌△QMP，‎ ‎∴NQ=PM=3，NG=PM﹣AG=3﹣2=1，‎ ‎∴BN=MQ=4+1=5，‎ ‎∴P（2，﹣5），Q（﹣1，0）‎ ‎∴PQ==，‎ ‎∴S△BPQ=PQ•PB==17；‎ 如图5，易得△QNB≌△PMQ，‎ ‎∴NQ=PM=3，‎ ‎∴P（2，﹣1），Q（5，0），‎ ‎∴PQ=，‎ ‎∴S△BPQ=PQ•PB==5，‎ ‎③若∠PBQ=90°，BQ=BP，如图6，‎ 过Q作QN⊥AB，交AB的延长线于N，‎ 易得：△PAB≌△BNQ，‎ ‎∵AB=2，NQ=3，AB≠NQ ‎∴此时不存在符合条件的P、Q．‎ ‎29．（2017•郴州）如图，已知抛物线y=ax2+x+c与x轴交于A，B两点，与y轴交于丁C，且A（2，0），C（0，﹣4），直线l：y=﹣x﹣4与x轴交于点D，点P是抛物线y=ax2+x+c上的一动点，过点P作PE⊥x轴，垂足为E，交直线l于点F．‎ ‎（1）试求该抛物线表达式；‎ ‎（2）如图（1），过点P在第三象限，四边形PCOF是平行四边形，求P点的坐标；‎ ‎（3）如图（2），过点P作PH⊥y轴，垂足为H，连接AC．‎ ‎①求证：△ACD是直角三角形；‎ ‎②试问当P点横坐标为何值时，使得以点P、C、H为顶点的三角形与△ACD相似？‎ ‎【解答】解：（1）由题意得：，解得：，‎ ‎∴抛物线的表达式为y=x2+x﹣4．‎ ‎（2）设P（m，m2+m﹣4），则F（m，﹣m﹣4）．‎ ‎∴PF=（﹣m﹣4）﹣（m2+m﹣4）=﹣m2﹣m．‎ ‎∵PE⊥x轴，‎ ‎∴PF∥OC．‎ ‎∴PF=OC时，四边形PCOF是平行四边形．‎ ‎∴﹣m2﹣m=4，解得：m=﹣或m=﹣8．‎ 当m=﹣时，m2+m﹣4=﹣，‎ 当m=﹣8时，m2+m﹣4=﹣4．‎ ‎∴点P的坐标为（﹣，﹣）或（﹣8，﹣4）．‎ ‎（3）①证明：把y=0代入y=﹣x﹣4得：﹣x﹣4=0，解得：x=﹣8．‎ ‎∴D（﹣8，0）．‎ ‎∴OD=8．‎ ‎∵A（2，0），C（0，﹣4），‎ ‎∴AD=2﹣（﹣8）=10．‎ 由两点间的距离公式可知：AC2=22+42=20，DC2=82+42=80，AD2=100，‎ ‎∴AC2+CD2=AD2．‎ ‎∴△ACD是直角三角形，且∠ACD=90°．‎ ‎②由①得∠ACD=90°．‎ 当△ACD∽△CHP时，=，即=或=，‎ 解得：n=0（舍去）或n=﹣5.5或n=﹣10.5．‎ 当△ACD∽△PHC时，=，即=或即=．‎ 解得：n=0（舍去）或n=2或n=﹣18．‎ 综上所述，点P的横坐标为﹣5.5或﹣10.5或2或﹣18时，使得以点P、C、H为顶点的三角形与△ACD相似．‎ ‎30．（2017•南宁）如图，已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A，B，C三点，其中C（0，3），∠BAC的平分线AE交y轴于点D，交BC于点E，过点D的直线l与射线AC，AB分别交于点M，N．‎ ‎（1）直接写出a的值、点A的坐标及抛物线的对称轴；‎ ‎（2）点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P的坐标；‎ ‎（3）证明：当直线l绕点D旋转时，+均为定值，并求出该定值．‎ ‎【解答】解：（1）∵C（0，3）．‎ ‎∴﹣9a=3，解得：a=﹣．‎ 令y=0得：ax2﹣2 x﹣9a=0，‎ ‎∵a≠0，‎ ‎∴x2﹣2 x﹣9=0，解得：x=﹣或x=3．‎ ‎∴点A的坐标为（﹣，0），B（3，0）．‎ ‎∴抛物线的对称轴为x=．‎ ‎（2）∵OA=，OC=3，‎ ‎∴tan∠CAO=，‎ ‎∴∠CAO=60°．‎ ‎∵AE为∠BAC的平分线，‎ ‎∴∠DAO=30°．‎ ‎∴DO=AO=1．‎ ‎∴点D的坐标为（0，1）‎ 设点P的坐标为（，a）．‎ 依据两点间的距离公式可知：AD2=4，AP2=12+a2，DP2=3+（a﹣1）2．‎ 当AD=PA时，4=12+a2，方程无解．‎ 当AD=DP时，4=3+（a﹣1）2，解得a=0或a=2（舍去），‎ ‎∴点P的坐标为（，0）．‎ 当AP=DP时，12+a2=3+（a﹣1）2，解得a=﹣4．‎ ‎∴点P的坐标为（，﹣4）．‎ 综上所述，点P的坐标为（，0）或（，﹣4）．‎ ‎（3）设直线AC的解析式为y=mx+3，将点A的坐标代入得：﹣m+3=0，解得：m=，‎ ‎∴直线AC的解析式为y=x+3．‎ 设直线MN的解析式为y=kx+1．‎ 把y=0代入y=kx+1得：kx+1=0，解得：x=﹣，‎ ‎∴点N的坐标为（﹣，0）．‎ ‎∴AN=﹣+=．‎ 将y=x+3与y=kx+1联立解得：x=．‎ ‎∴点M的横坐标为．‎ 过点M作MG⊥x轴，垂足为G．则AG=+．‎ ‎∵∠MAG=60°，∠AGM=90°，‎ ‎∴AM=2AG=+2=．‎ ‎∴+=+=+===．‎ ‎31．（2017•吉林）《函数的图象与性质》拓展学习片段展示：‎ ‎【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣经过原点O，与x轴的另一个交点为A，则a=　　．‎ ‎【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．‎ ‎【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围．‎ ‎【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围．‎ ‎【解答】解：【问题】‎ ‎∵抛物线y=a（x﹣2）2﹣经过原点O，‎ ‎∴0=a（0﹣2）2﹣，‎ a=，‎ 故答案为：；‎ ‎【操作】：如图①，抛物线：y=（x﹣2）2﹣，‎ 对称轴是：直线x=2，由对称性得：A（4，0），‎ 沿x轴折叠后所得抛物线为：y=﹣（x﹣2）2+‎ 如图②，图象G对应的函数解析式为：y=；‎ ‎【探究】：如图③，由题意得：‎ 当y=1时，（x﹣2）2﹣=1，‎ 解得：x1=2+，x2=2﹣，‎ ‎∴C（2﹣，1），F（2+，1），‎ 当y=1时，﹣（x﹣2）2+=1，‎ 解得：x1=3，x2=1，‎ ‎∴D（1，1），E（3，1），‎ 由图象得：图象G在直线l上方的部分，当1＜x＜2或x＞2+时，函数y随x增大而增大；‎ ‎【应用】：∵D（1，1），E（3，1），‎ ‎∴DE=3﹣1=2，‎ ‎∵S△PDE=DE•h≥1，‎ ‎∴h≥1；‎ ‎①当P在C的左侧或F的右侧部分时，设P[m，]，‎ ‎∴h=（m﹣2）2﹣﹣1≥1，‎ ‎（m﹣2）2≥10，‎ m﹣2≥或m﹣2≤﹣，‎ m≥2+或m≤2﹣，‎ ‎②如图③，作对称轴交抛物线G于H，交直线CD于M，交x轴于N，‎ ‎∵H（2，），‎ ‎∴HM=﹣1=＜1，‎ ‎∴点P不可能在DE的上方；‎ ‎③∵MN=1，‎ 且O（0，0），A（4，0），‎ ‎∴P不可能在CO（除O点）、OD、EA（除A点）、AF上，‎ ‎∴P与O或A重合时，符合条件，‎ ‎∴m=0或m=4；‎ 综上所述，△PDE的面积不小于1时，m的取值范围是：m=0或m=4或m≤2﹣或m≥2+．‎ ‎32．（2017•镇江）如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数y=x2+bx（b＜0）的图象经过点B，顶点为点D．‎ ‎（1）当t=12时，顶点D到x轴的距离等于　　；‎ ‎（2）点E是二次函数y=x2+bx（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OE•EA的最大值及取得最大值时的二次函数表达式；‎ ‎（3）矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数y=x2+bx（b＜0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．‎ ‎【解答】解：（1）当t=12时，B（4，12）．‎ 将点B的坐标代入抛物线的解析式得：16+4b=12，解得：b=﹣1，‎ ‎∴抛物线的解析式y=x2﹣x．‎ ‎∴y=（x﹣）2﹣．‎ ‎∴D（，）．‎ ‎∴顶点D与x轴的距离为．‎ 故答案为：．‎ ‎（2）将y=0代入抛物线的解析式得：x2+bx=0，解得x=0或x=﹣b，‎ ‎∵OA=4，‎ ‎∴AE=4﹣（﹣b）=4+b．‎ ‎∴OE•AE=﹣b（4+b）=﹣b2﹣4b=﹣（b+2）2+4，‎ ‎∴OE•AE的最大值为4，此时b的值为﹣2，‎ ‎∴抛物线的表达式为y=x2﹣2x．‎ ‎（3）过D作DG⊥MN，垂足为G，过点F作FH⊥CO，垂足为H．‎ ‎∵△DMN≌△FOC，‎ ‎∴MN=CO=t，DG=FH=2．‎ ‎∵D（﹣，﹣），‎ ‎∴N（﹣+，﹣+2），即（，）．‎ 把点N和坐标代入抛物线的解析式得：=（）2+b•（），‎ 解得：t=±2．‎ ‎∵t＞0，‎ ‎∴t=2．‎ ‎33．（2017•绥化）在平面直角坐标系中，直线y=﹣x+1交y轴于点B，交x轴于点A，抛物线y=﹣x2+bx+c经过点B，与直线y=﹣x+1交于点C（4，﹣2）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图，横坐标为m的点M在直线BC上方的抛物线上，过点M作ME∥‎ y轴交直线BC于点E，以ME为直径的圆交直线BC于另一点D，当点E在x轴上时，求△DEM的周长．‎ ‎（3）将△AOB绕坐标平面内的某一点按顺时针方向旋转90°，得到△A1O1B1，点A，O，B的对应点分别是点A1，O1，B1，若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的坐标．‎ ‎【解答】解：（1）∵直线y=﹣x+1交y轴于点B，‎ ‎∴B（0，1），‎ ‎∵抛物线y=﹣x2+bx+c经过点B和点C（4，﹣2）．‎ ‎∴，‎ 解得：，‎ ‎∴抛物线的解析式为：y=﹣x2+x+1；‎ ‎（2）如图1，∵直线y=﹣x+1交x轴于点A，‎ 当y=0时，﹣x+1=0，‎ x=，‎ ‎∴A（，0），‎ ‎∴OA=，‎ 在Rt△AOB中，‎ ‎∵OB=1，‎ ‎∴AB=，‎ ‎∴sin∠ABO=，cos∠ABO==，‎ ‎∵ME∥x轴，‎ ‎∴∠DEM=∠ABO，‎ ‎∵以ME为直径的圆交直线BC于另一点D，‎ ‎∴∠EDM=90°，‎ ‎∴DE=ME•cos∠DEM=ME，‎ DM=ME•sin∠DEM=ME，‎ 当点E在x轴上时，E和A重合，则m=OA=，‎ 当x=时，y=﹣×+×+1=；‎ ‎∴ME=，‎ ‎∴DE==，DM==，‎ ‎∴△DEM的周长=DE+DM+ME=++=；‎ ‎（3）由旋转可知：O1A1⊥x轴，O1B1⊥y轴，设点A1的横坐标为x，则点B1的横坐标为x+1，‎ ‎∵O1A1⊥x轴，‎ ‎∴点O1，A1不可能同时落在抛物线上，分以下两种情况：‎ ‎①如图2，当点O1，B1同时落在抛物线上时，‎ 点O1，B1的纵坐标相等，‎ ‎∴﹣=﹣（x+1）2+（x+1）+1，‎ 解得：x=，‎ 此时点A1的坐标为（，），‎ ‎②如图3，当点A1，B1同时落在抛物线上时，‎ 点B1的纵坐标比点A1的纵坐标大，‎ ‎﹣=﹣（x+1）2+（x+1）+1，‎ 解得：x=﹣，‎ 此时A1（﹣，），‎ 综上所述，点A1（，）或（﹣，）．‎ ‎34．（2017•鄂州）已知，抛物线y=ax2+bx+3（a＜0）与x轴交于A（3，0）、B两点，与y轴交于点C，抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE=．‎ ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）求证：直线DE是△ACD外接圆的切线；‎ ‎（3）在直线AC上方的抛物线上找一点P，使S△ACP=S△ACD，求点P的坐标；‎ ‎（4）在坐标轴上找一点M，使以点B、C、M为顶点的三角形与△ACD相似，直接写出点M的坐标．‎ ‎【解答】解：（1）∵抛物线的对称轴是直线x=1，点A（3，0），‎ ‎∴根据抛物线的对称性知点B的坐标为（﹣1，0），OA=3，‎ 将A（3，0），B（﹣1，0）代入抛物线解析式中得：，‎ 解得：，‎ ‎∴抛物线解析式为y=﹣x2+2x+3；‎ 当x=1时，y=4，‎ ‎∴顶点D（1，4）．‎ ‎（2）当=0时，‎ ‎∴点C的坐标为（0，3），‎ ‎∴AC==3，CD==，AD==2，‎ ‎∴AC2+CD2=AD2，‎ ‎∴△ACD为直角三角形，∠ACD=90°．‎ ‎∴AD为△ACD外接圆的直径，‎ ‎∵点E在 轴C点的上方，且CE=．‎ ‎∴E（0，）‎ ‎∴AE==DE==，‎ ‎∴DE2+AD2=AE2，‎ ‎∴△AED为直角三角形，∠ADE=90°．‎ ‎∴AD⊥DE，‎ 又∵AD为△ACD外接圆的直径，‎ ‎∴DE是△ACD外接圆的切线；‎ ‎（3）设直线AC的解析式为y=kx+b，‎ 根据题意得：，‎ 解得：，∴直线AC的解析式为y=﹣x+3，‎ ‎∵A（3，0），D（1，4），‎ ‎∴线段AD的中点N的坐标为（2，2），‎ 过点N作NP∥AC，交抛物线于点P，‎ 设直线NP的解析式为y=﹣x+c，‎ 则﹣2+c=2，解得：c=4，‎ ‎∴直线NP的解析式为y=﹣x+4，‎ 由y=﹣x+4，y=﹣x2+2x+3联立得：﹣x2+2x+3=﹣x+4，‎ 解得：x=或x=，‎ ‎∴y=，或y=‎ ‎∴P（，）或（，）；‎ ‎（4）分三种情况：①M恰好为原点，满足△CMB∽△ACD，M（0，0）；‎ ‎②M在x轴正半轴上，△MCB∽△ACD，此时M（9，0）；‎ ‎③M在y轴负半轴上，△CBM∽△ACD，此时M（0，﹣）；‎ 综上所述，点M的坐标为（0，0）或（9，0）或（0，﹣）．‎ ‎35．（2017•淮安）如图①，在平面直角坐标系中，二次函数y=﹣x2+bx+c的图象与坐标轴交于A，B，C三点，其中点A的坐标为（﹣3，0），点B的坐标为（4，0），连接AC，BC．动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒．连接PQ．‎ ‎（1）填空：b=　　，c=　4　；‎ ‎（2）在点P，Q运动过程中，△APQ可能是直角三角形吗？请说明理由；‎ ‎（3）在x轴下方，该二次函数的图象上是否存在点M，使△PQM是以点P为直角顶点的等腰直角三角形？若存在，请求出运动时间t；若不存在，请说明理由；‎ ‎（4）如图②，点N的坐标为（﹣，0），线段PQ的中点为H，连接NH，当点Q关于直线NH的对称点Q′恰好落在线段BC上时，请直接写出点Q′的坐标．‎ ‎【解答】解：（1）设抛物线的解析式为y=a（x+3）（x﹣4）．将a=﹣代入得：y=﹣x2+x+4，‎ ‎∴b=，c=4．‎ ‎（2）在点P、Q运动过程中，△APQ不可能是直角三角形．‎ 理由如下：连结QC．‎ ‎∵在点P、Q运动过程中，∠PAQ、∠PQA始终为锐角，‎ ‎∴当△APQ是直角三角形时，则∠APQ=90°．‎ 将x=0代入抛物线的解析式得：y=4，‎ ‎∴C（0，4）．‎ ‎∵AP=OQ=t，‎ ‎∴PC=5﹣t，‎ ‎∵在Rt△AOC中，依据勾股定理得：AC=5，在Rt△COQ中，依据勾股定理可知：CQ2=t2+16，在Rt△CPQ中依据勾股定理可知：PQ2=CQ2﹣CP2，在Rt△APQ中，AQ2﹣AP2=PQ2，‎ ‎∴CQ2﹣CP2=AQ2﹣AP2，即（3+t）2﹣t2=t2+16﹣（5﹣t）2，解得：t=4.5．‎ ‎∵由题意可知：0≤t≤4，‎ ‎∴t=4.5不和题意，即△APQ不可能是直角三角形．‎ ‎（3）如图所示：‎ 过点P作DE∥x轴，分别过点M、Q作MD⊥DE、QE⊥DE，垂足分别为D、E，MD交x轴与点F，过点P作PG⊥x轴，垂足为点G，则PG∥y轴，∠E=∠D=90°．‎ ‎∵PG∥y轴，‎ ‎∴△PAG∽△ACO，‎ ‎∴==，即==，‎ ‎∴PG=t，AG=t，‎ ‎∴PE=GQ=GO+OQ=AO﹣AG+OQ=3﹣t+t=3+t，DF=GP=t．‎ ‎∵∠MPQ=90°，∠D=90°，‎ ‎∴∠DMP+∠DPM=∠EPQ+∠DPM=90°，‎ ‎∴∠DMP=∠EPQ．‎ 又∵∠D=∠E，PM=PQ，‎ ‎∴△MDP≌PEQ，‎ ‎∴PD=EQ=t，MD=PE=3+t，‎ ‎∴FM=MD﹣DF=3+t﹣t=3﹣t，OF=FG+GO=PD+OA﹣AG=3+t﹣t=3+t，‎ ‎∴M（﹣3﹣t，﹣3+t）．‎ ‎∵点M在x轴下方的抛物线上，‎ ‎∴﹣3+t=﹣×（﹣3﹣t）2+×（﹣3﹣t）+4，解得：t=．‎ ‎∵0≤t≤4，‎ ‎∴t=．‎ ‎（4）如图所示：连结OP，取OP的中点R，连结RH，NR，延长NR交线段BC与点Q′．‎ ‎∵点H为PQ的中点，点R为OP的中点，‎ ‎∴EH=QO=t，RH∥OQ．‎ ‎∵A（﹣3，0），N（﹣，0），‎ ‎∴点N为OA的中点．‎ 又∵R为OP的中点，‎ ‎∴NR=AP=t，‎ ‎∴RH=NR，‎ ‎∴∠RNH=∠RHN．‎ ‎∵RH∥OQ，‎ ‎∴∠RHN=∠HNO，‎ ‎∴∠RNH=∠HNO，即NH是∠QNQ′的平分线．‎ 设直线AC的解析式为y=mx+n，把点A（﹣3，0）、C（0，4）代入得：，‎ 解得：m=，n=4，‎ ‎∴直线AC的表示为y=x+4．‎ 同理可得直线BC的表达式为y=﹣x+4．‎ 设直线NR的函数表达式为y=x+s，将点N的坐标代入得：×（﹣）+s=0，解得：s=2，‎ ‎∴直线NR的表述表达式为y=x+2．‎ 将直线NR和直线BC的表达式联立得：，解得：x=，y=，‎ ‎∴Q′（，）．‎ ‎36．（2017•雨城区校级自主招生）如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线 y=﹣x2+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以每秒1个单位的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以每秒个单位的速度匀速运动，连接PQ，设运动时间为t秒．‎ ‎（1）求抛物线的解析式；‎ ‎（2）问：当t为何值时，△APQ为直角三角形；‎ ‎（3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；‎ ‎（4）设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．‎ ‎【解答】解：（1）当y=0时，﹣x+3=0，解得x=3，则A点坐标为（3，0），‎ 当x=0时，y=﹣x+3=3，则B点坐标为（0，3），‎ 将A（3，0），B（0，3）代入y=﹣x2+bx+c得，解得，‎ ‎∴抛物线的解析式为y=﹣x2+2x+3；‎ ‎（2）OP=t，AQ=t，则PA=3﹣t，‎ ‎∵OA=OB=3，∠BOA=90°，‎ ‎∴∠QAP=45°．‎ 当∠PQA=90°时，如图①，PA=AQ，即3﹣t=•t，解得t=1；‎ 当∠APQ=90°时，如图②，AQ=AP，即t=•（3﹣t），解得t=；‎ 综上所述，当t=1或t=时，△PQA是直角三角形；‎ ‎（3）如图③，延长FQ交x轴于点H，设点P的坐标为（t，0），则点E的坐标为（t，﹣t+3），‎ 易得△AQH为等腰直角三角形，‎ ‎∴AH=HQ=AQ=•t=t，‎ ‎∴点Q的坐标为（3﹣t，t），点F的坐标为[3﹣t，﹣（3﹣t）2+2（3﹣t）+3）]，‎ ‎∴FQ=﹣（3﹣t）2+2（3﹣t）+3）﹣t=﹣t2+3t，‎ ‎∵EP∥FQ，EF∥PQ，‎ ‎∴四边形PQFE为平行四边形，‎ ‎∴EP=FQ．即3﹣t=3t﹣t2，解得t1=1，t2=3（舍去），‎ ‎∴点F的坐标为（2，3）；‎ ‎（4）存在．‎ 如图④所示：OP=t，AQ=t，则BQ=3﹣t，‎ ‎∵y=﹣x2+2x+3=﹣（x﹣1）2+4，‎ ‎∴点M的坐标为（1，4），‎ ‎∴MB==，‎ 而AB=3，AM==2，‎ ‎∴AB2+BM2=AM2，‎ ‎∴△ABM为直角三角形，∠ABM=90°，‎ ‎∵∠QBM=∠BOP，‎ ‎∴当=时，△BOP∽△QBM时，即=，‎ 整理得t2﹣3t+3=0，△=32﹣4×1×3＜0，方程无实数解：‎ 当=时，△BOP∽△MBQ，即=，解得t=，‎ 综上所述，当t=时，以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似．‎ ‎37．（2017•余姚市校级自主招生）如图，直线y=﹣x+3与x轴，y轴分别相交于点B，C，经过B，C两点的抛物线y=ax2+bx+c与x轴的另一交点为A，顶点为P，且对称轴是直线x=2．‎ ‎（1）求该抛物线的函数表达式；‎ ‎（2）请问在抛物线上是否存在点Q，使得以点B，C，Q为顶点的三角形为直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由；‎ ‎（3）过S（0，4）的动直线l交抛物线于M，N两点，试问抛物线上是否存在定点T，使得不过定点T的任意直线l都有∠MTN=90°？若存在，请求出点T的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）∵直线y=﹣x+3与x轴，y轴分别相交于点B，C，‎ ‎∴B（3，0），C（0，3），‎ ‎∵对称轴为直线x=2，‎ ‎∴设该抛物线的函数表达式为y=a（x﹣1）（x﹣3），‎ 把C（0，3）代入得3a=3，解得a=1，‎ ‎∴该抛物线的函数表达式y=（x﹣1）（x﹣3）=x2﹣4x+3；‎ ‎（2）存在，设过B点垂直BC的直线的解析式为y=x+b，‎ 把B（3，0）代入得b=﹣3，‎ 则直线的解析式为y=x﹣3，‎ 依题意有，‎ 解得，，‎ ‎∴Q1（2，﹣1），‎ 过C点垂直BC的直线解析式为y=x+3，‎ 依题意有，‎ 解得，，‎ ‎∴Q2（5，8），‎ 以BC为斜边，设β（a，a2﹣4a+3），则 a2+（a2﹣4a）2+（a﹣3）2+（a2﹣4a+3）2=18，‎ a3﹣8a2+20a﹣15=0，‎ ‎（a﹣3）（a2﹣5a+5）=0，‎ 解得a1=3，a2=，‎ ‎∴Q3（，），Q4（，），‎ ‎∴存在点Q，使得以点B，C，Q为顶点的三角形为直角三角形；‎ ‎（3）设M（x1，y1），N（x2，y2），T（a，b），‎ 过T作PQ∥x轴，过M，N作MP⊥PQ于P，NQ⊥PQ于Q，‎ 则∠MTN=90°，‎ 则△MPT∽△TQN，‎ ‎∴=，‎ a（x1+x2）﹣a2﹣x1x2=y1y2﹣b（y1+y2）+b2，‎ 其中x1，x2，y1，y2是的解，‎ ‎∴x2﹣（4+k）x﹣1=0，‎ x1x2=﹣1，‎ x1+x2=k+4，‎ y1y2=k2x1x2+4k（x1+x2）+16=﹣k2+4k（k+4）+16，‎ y1+y2=k（k+4）+8，‎ ‎1+a（k+4）﹣a2=﹣k2+4k（k+4）+16﹣b（k2+4k+8）+b2，‎ ‎1+ak+4a﹣a2=﹣k3+4k2+16k+16﹣bk2﹣4bk﹣8b+b2，‎ ‎∴（3﹣b）k2+（16﹣4b﹣a）k+a2﹣4a﹣8b+b2+15=0，‎ ‎∵y=kx+b有无数条，‎ ‎∴k为任何实数，3﹣b=0，16﹣4b﹣a=0，a2﹣4a﹣8b+b2+15=0，‎ 解得a=4，b=3，‎ 存在点T（4，3）使得不过定点T的任意直线l都有∠MTN=90°．‎ ‎38．（2017•信丰县自主招生）如图，抛物线C1：y1=ax2+2ax（a＞0）与x轴交于点A，顶点为点P．‎ ‎（1）直接写出抛物线C1的对称轴是　直线x=﹣1　，用含a的代数式表示顶点P的坐标　（﹣1，﹣a）　；‎ ‎（2）把抛物线C1绕点M（m，0）旋转180°得到抛物线C2（其中m＞0），抛物线C2与x轴右侧的交点为点B，顶点为点Q．‎ ‎①当m=1时，求线段AB的长；‎ ‎②在①的条件下，是否存在△ABP为等腰三角形，若存在请求出a的值，若不存在，请说明理由；‎ ‎③当四边形APBQ为矩形时，请求出m与a之间的数量关系，并直接写出当a=3时矩形APBQ的面积．‎ ‎【解答】解：（1）∵抛物线C1：y1=ax2+2ax=a（x+1）2﹣a，‎ ‎∴x=﹣1，P（﹣1，﹣a）‎ 故答案为：直线x=﹣1，（﹣1，﹣a），‎ ‎（2）①由旋转知，MA=MB，‎ 当y1=0时，x1=﹣2，x2=0，‎ ‎∴A（﹣2，0），‎ ‎∴AO=2，‎ ‎∵M（1，0），‎ ‎∴AM=3，‎ ‎∴AB=2MA=2×3=6；‎ ‎②∵A（﹣2，0），AB=6，‎ ‎∴B（4，0）‎ ‎∵A（﹣2，0），P（﹣1，﹣a），‎ ‎∴，‎ 当AB=AP时，1+a2=62，解得：（负值已舍去）；‎ 当AB=BP时，25+a2=62，解得：（负值已舍去）；‎ 当AP=BP时，1+a2=25+a2，不成立，‎ 即当a 取或时，△ABP为等腰三角形；‎ ‎③如图，过点P作PH⊥x轴于H，‎ ‎∵点A与点B，点P与点Q均关于M点成中心对称，‎ 故四边形APBQ为平行四边形，‎ 当∠APB=90°时，四边形APBQ为矩形，‎ 此时△APH∽△PBH，‎ ‎∴，‎ 即，‎ ‎∴a2=2m+3，‎ ‎∴，‎ 当a=3时，，‎ ‎∴S=（2m+4）a=（2×3+4）×3=30．‎ ‎39．（2017•江阴市自主招生）已知二次函数y=ax2﹣4ax+a2+2（a＜0）图象的顶点G在直线AB上，其中 A（﹣，0）、B（0，3），对称轴与x轴交于点E．‎ ‎（1）求二次函数y=ax2﹣4ax+a2+2的关系式；‎ ‎（2）点P在对称轴右侧的抛物线上，且AP平分四边形GAEP的面积，求点P坐标；‎ ‎（3）在x轴上方，是否存在整数m，使得当＜x≤时，抛物线y随x增大而增大？若存在，求出所有满足条件的m值；若不存在，请说明理由．‎ ‎【解答】解（1）设直线AB的关系式为y=kx+b，‎ 将点A（﹣，0）、B（0，3）代入y=kx+b中，‎ ‎，解得：，‎ ‎∴直线AB的关系式为y=2x+3．‎ ‎∵抛物线y=ax2﹣4ax+a2+2=a（x﹣2）2+a2﹣4a+2，‎ ‎∴点G（2，a2﹣4a+2）．‎ ‎∵点G在直线AB上，‎ ‎∴a2﹣4a+2=4+3=7，‎ ‎∴a=﹣1，a=5（舍去），‎ ‎∴二次函数关系式为y=﹣x2+4x+3．‎ ‎（2）∵AP平分四边形GAEP的面积，‎ ‎∴2S△AEP=S四边形GAEP．‎ 设点P的坐标为（t，﹣t2+4t+3），‎ ‎∴2××（2+）（﹣t2+4t+3）=×7×（2+）+×7×（t﹣2），‎ 整理得：2t2﹣6 t﹣3=0，‎ 解得：t1=，t2=（舍去），‎ ‎∴点P的坐标为（，6+）．‎ ‎（3）当y=﹣x2+4x+3=0时，x1=2﹣，x2=2+，‎ ‎∴抛物线与x轴交点C（2﹣，0），D（2+，0）．‎ ‎∵在x轴上方，抛物线y随x增大而增大，‎ ‎∴2﹣＜x≤2．‎ 又∵＜x≤，‎ ‎∴，‎ 解得：4﹣3≤m≤﹣．‎ ‎∵整数m为整数，‎ ‎∴m为﹣3，﹣2、﹣1．‎ 又∵＜，‎ ‎∴m＞﹣，‎ ‎∴m取﹣2、﹣1．‎ ‎40．（2017•哈尔滨）如图，在平面直角坐标系中，点O为坐标原点，抛物线y=x2+bx+c交x轴于A、B两点，交y轴于点C，直线y=x﹣3经过B、C两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）过点C作直线CD⊥y轴交抛物线于另一点D，点P是直线CD下方抛物线上的一个动点，且在抛物线对称轴的右侧，过点P作PE⊥x轴于点E，PE交CD于点F，交BC于点M，连接AC，过点M作MN⊥AC于点N，设点P的横坐标为t，线段MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；‎ ‎（3）在（2）的条件下，连接PC，过点B作BQ⊥PC于点Q（点Q在线段PC上），BQ交CD于点T，连接OQ交CD于点S，当ST=TD时，求线段MN的长．‎ ‎【解答】解：（1）∵直线y=x﹣3经过B、C两点，‎ ‎∴B（3，0），C（0，﹣3），‎ ‎∵y=x2+bx+c经过B、C两点，‎ ‎∴，‎ 解得，‎ 故抛物线的解析式为y=x2﹣2x﹣3；‎ ‎（2）如图1，y=x2﹣2x﹣3，‎ y=0时，x2﹣2x﹣3=0，‎ 解得x1=﹣1，x2=3，‎ ‎∴A（﹣1，0），‎ ‎∴OA=1，OB=OC=3，‎ ‎∴∠ABC=45°，AC=，AB=4，‎ ‎∵PE⊥x轴，‎ ‎∴∠EMB=∠EBM=45°，‎ ‎∵点P的横坐标为1，‎ ‎∴EM=EB=3﹣t，‎ 连结AM，‎ ‎∵S△ABC=S△AMC+S△AMB，‎ ‎∴AB•OC=AC•MN+AB•EM，‎ ‎∴×4×3=×d+×4（3﹣t），‎ ‎∴d=t；‎ ‎（3）如图2，‎ ‎∵y=x2﹣2x﹣3=（x﹣1）2﹣4，‎ ‎∴对称轴为x=1，‎ ‎∴由抛物线对称性可得D（2，﹣3），‎ ‎∴CD=2，‎ 过点B作BK⊥CD交直线CD于点K，‎ ‎∴四边形OCKB为正方形，‎ ‎∴∠OBK=90°，CK=OB=BK=3，‎ ‎∴DK=1，‎ ‎∵BQ⊥CP，‎ ‎∴∠CQB=90°，‎ 过点O作OH⊥PC交PC延长线于点H，OR⊥BQ交BQ于点I交BK于点R，OG⊥OS交KB于G，‎ ‎∴∠OHC=∠OIQ=∠OIB=90°，‎ ‎∴四边形OHQI为矩形，‎ ‎∵∠OCQ+∠OBQ=180°，‎ ‎∴∠OBG=∠OCS，‎ ‎∵OB=OC，∠BOG=∠COS，‎ ‎∴△OBG≌△OCS，‎ ‎∴QG=OS，∠GOB=∠SOC，‎ ‎∴∠SOG=90°，‎ ‎∴∠ROG=45°，‎ ‎∵OR=OR，‎ ‎∴△OSR≌△OGR，‎ ‎∴SR=GR，‎ ‎∴SR=CS+BR，‎ ‎∵∠BOR+∠OBI=90°，∠IBO+∠TBK=90°，‎ ‎∴∠BOR=∠TBK，‎ ‎∴tan∠BOR=tan∠TBK，‎ ‎∴=，‎ ‎∴BR=TK，‎ ‎∵∠CTQ=∠BTK，‎ ‎∴∠QCT=∠TBK，‎ ‎∴tan∠QCT=tan∠TBK，‎ 设ST=TD=m，‎ ‎∴SK=2m+1，CS=2﹣2m，TK=m+1=BR，SR=3﹣m，RK=2﹣m，‎ 在Rt△SKR中，‎ ‎∵SK2+RK2=SR2，‎ ‎∴（2m+1）2+（2﹣m）2=（3﹣m）2，‎ 解得m1=﹣2（舍去），m2=；‎ ‎∴ST=TD=，TK=，‎ ‎∴tan∠TBK==÷3=，‎ ‎∴tan∠PCD=，‎ 过点P作PE′⊥x轴于E′交CD于点F′，‎ ‎∵CF′=OE′=t，‎ ‎∴PF′=t，‎ ‎∴PE′=t+3，‎ ‎∴P（t，﹣t﹣3），‎ ‎∴﹣t﹣3=t2﹣2t﹣3，‎ 解得t1=0（舍去），t2=．‎ ‎∴MN=d=t=×=．‎