2015中考数学几何压轴题

2015中考数学几何压轴题

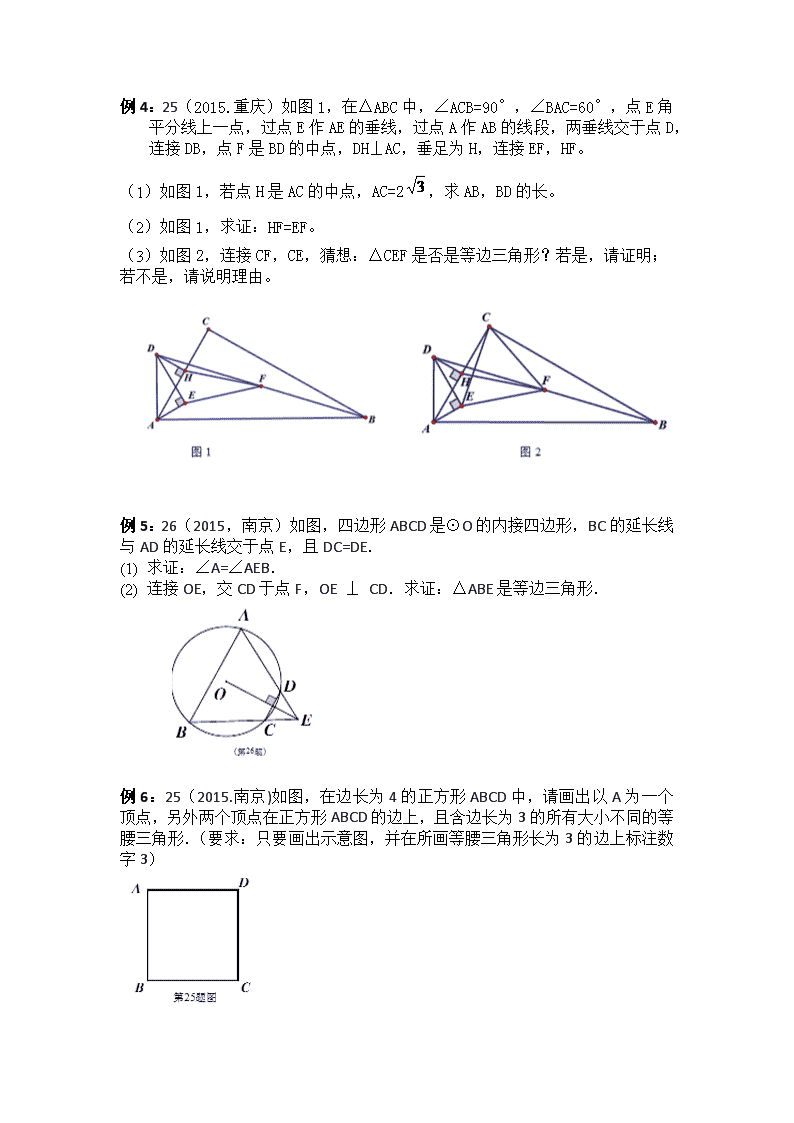
例1：28.（2015.北京）在正方形ABCD中，BD是一条对角线，点P在射线CD上（与点C、D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于H，连接AH，PH。 ‎ (1) 若点P在线段CD上，如图1。 ‎ ‎①依题意补全图1；‎ ‎②判断AH与PH的数量关系与位置关系并加以证明； ‎ 若点P在线段CD的延长线上，∠AHQ=152°，正方形ABCD的边长为1，请写出求DP长的思路。（可以不写出计算结果．．．．．．．．．）‎ ‎ ‎ 例2：25(2015.上海) 已知：如图，AB是半圆O的直径，弦CD∥AB，动点P、Q分别在线段OC、CD上，且DQ＝OP，AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C、D不重合)，AB＝20，cos∠AOC＝4/5．设OP＝x，△CPF的面积为y． ‎ ‎(1)求证：AP＝OQ；‎ (2) 求y关于x的函数关系式，并写出它的定义域； ‎ (3) 当△OPE是直角三角形时，求线段OP的长．‎ ‎ ‎ 例3：24（2015.天津）将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（，0），点B（0，1），点O（0，0）. 过边OA上的动点M（点M不与点O，A重合）作MN⊥AB于点N，沿着MN折叠该纸片，得顶点A的对应点A′. 设OM=m，折叠后的△A′MN与四边形OMNB重叠部分的面积为S. ‎ ‎（Ⅰ）如图①，当点A′与顶点B重合时，求点M的坐标； ‎ ‎（Ⅱ）如图②，当点A′落在第二象限时，A′M与OB相交于点C，试用含m的式子表示S； ‎ ‎（Ⅲ）当S=时，求点M的坐标（直接写出结果即可）．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例4：25（2015.重庆）如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E角平分线上一点，过点E作AE的垂线，过点A作AB的线段，两垂线交于点D，连接DB，点F是BD的中点，DH⊥AC，垂足为H，连接EF，HF。 ‎ （1） 如图1，若点H是AC的中点，AC=2，求AB，BD的长。 ‎ （2） 如图1，求证：HF=EF。 ‎ （3） 如图2，连接CF，CE，猜想：△CEF是否是等边三角形？若是，请证明；若不是，请说明理由。‎ ‎ ‎ ‎ ‎ 例5：26（2015，南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE． ‎ (1) 求证：∠A=∠AEB． ‎ (2) 连接OE，交CD于点F，OE ⊥ CD．求证：△ABE是等边三角形．‎ ‎ ‎ ‎ ‎ 例6：25（2015.南京)如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）‎ ‎ ‎ ‎ ‎ 例7：24.（2015.广州） 如图10，四边形OMTN中，OM=ON，TM=TN，我们把这种两组邻边分别相等的四边形叫做筝形. ‎ ‎（1）试探究筝形对角线之间的位置关系，并证明你的结论； ‎ ‎（2）在筝形ABCD中，已知AB=AD=5，BC=CD，BC>AB，BD，AC为对角线，BD=8. ‎ ‎①是否存在一个圆使得A，B，C，D四个点都在这个圆上？若存在，求出圆的半径；若不存在，请说明理由； ‎ ‎ ②过点B作BF⊥CD，垂足为F，BF交AC于点E，连接DE.当四边形ABED为菱形时，求点F到AB的距离.‎ ‎ ‎ ‎ ‎ 例8：22(2015年浙江杭州12分）如图，在△ABC中(BC>AC)，∠ACB=90°，点D在AB边上，DE⊥AC于点E ‎ （1） 若AD/DB=1/3=，AE=2，求EC的长 ‎ （2） 设点F在线段EC上，点G在射线CB上，以F，C，G为顶点的三角形与△EDC有一个锐角相等，FG交CD于点P，问：线段CP可能是△CFG的高线还是中线？或两者都有可能？请说明理由 ‎ ‎ 例9：27（2015.成都） 已知,ACEC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90°。 ‎ （1） 如图①，当四边形ABCD和EFCG均为正方形时，连接BF。 ‎ 1) 求证：△CAED△CBF；‎ 2) 若BE=1,AE=2，求CE的长。 ‎ （2） 如图②，当四边形ABCD和EFCG均为矩形，且AB/BC=EF/FC时，若BE=1,AE=2,CE=3，求k的值； ‎ （3） 如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设,,BE=m，AE=n，CE=p，试探究,,m、n、p三者之间满足的等量关系。（直接写出结果，不必写出解答过程） ‎ ‎ ‎ ‎ ‎ 例10：22（2015.长沙）如图，在菱形ABCD中，AB=2，∠ABC=60°，对角线AC、BD相交于点O，将对角线AC所在的直线绕点O顺时针旋转角α（0°<α<90°）后得直线l，直线l与AD、BC两边分别相交于点E和点F。 ‎ （1） 求证：△AOE≌△COF； ‎ 当α=30°时，求线段EF的长度。‎ ‎ ‎ 例11：24（2015.长沙）.如图，在直角坐标系中，⊙M经过原点O（0,0），点A(,0)与点B(0,-，点D在劣弧 OA上，连接BD交x轴于点C，且∠COD=∠CBO。 ‎ （1） 求⊙M的半径；‎ （2） 求证：BD平分∠ABO； ‎ ‎（3）在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标。‎ ‎ ‎ ‎ ‎ 例12：25(2015.福州)如图.在锐角中，D，E分别为AB, BC中点, F为AC上一点，且∠AFE=∠A，DM//EF交AC于点M ‎ ‎(1)求证: DM=DA ‎ ‎(2)点G在BE上, 且∠BDG=∠C.如图②,求证:△DEG∽△ECF ‎（3）在图②中.取CE上一点H，使∠CFH=∠B. 若BG=1 求EH的长. ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例13：23（2015.沈阳）如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B的坐标为（60，0），OA=AB，∠OAB=90°，OC=50．点P是线段OB上的一个动点（点P不与点O、B重合），过点P与y轴平行的直线l交边OA或边AB于点Q，交边OC或边BC于点R，设点P横坐标为t，线段QR的长度为m．已知t=40时，直线l恰好经过点C．‎ ‎（1）求点A和点C的坐标； ‎ ‎（2）当0＜t＜30时，求m关于t的函数关系式； ‎ ‎（3）当m=35时，请直接写出t的值； ‎ ‎（4）直线l上有一点M，当∠PMB+∠POC=90°，且△PMB的周长为60时，请直接写出满足条件的点M的坐标．‎ ‎ ‎ ‎ ‎ 例14：24（2015.沈阳）如图，在▱ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将▱ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G． ‎ ‎（1）当点H与点C重合时． ‎ ‎ ①填空：点E到CD的距离是 ； ②求证：△BCE≌△GCF； ③求△CEF的面积； ‎ （1） 当点H落在射线BC上，且CH=1时，直线EH与直线CD交于点M，请直接写出△MEF的面积． ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例15：26. （2015.哈尔滨） AB,CD是⊙O的两条弦，直线AB，CD互相垂直，垂足为点E，连接AD，过点B作BF⊥AD,垂足为点F，直线BF交直线CD于点G. ‎ ‎（1） 如图1，档点E在⊙O外时，连接BC，求证BE平分∠GBC； ‎ ‎（2） 如图2，当点E在⊙O内时，连接AC，AG,求证：AC=AG； ‎ ‎（3） 如图3，在（2）的条件下，连接BO并延长交AD于点H，若BH平分∠ABF,AG=4，tan∠D=，求线段AH的长.‎ ‎ ‎ ‎ ‎ 例16：24.（2015.南昌）我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1，图2，图3中，AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c. 特例探索 ‎ ‎（1）如图1，当∠ABE=45°，c=2时，a= ，b= ； ‎ ‎ 如图2，当∠ABE=30°，c=4时， a= ，b= ； ‎ ‎ ‎ 归纳证明 ‎ ‎ （2）请你观察（1）中的计算结果，猜想a2b2c2三者之间的关系，用等式表示出来，并利用图3证 明你发现的关系式； ‎ ‎ 拓展应用 ‎ ‎ （3）如图4，在□ABCD中，点E,F,G分别是AD,BC,CD的中点，BE⊥EG, AD= 2,AB=3. ‎ 求AF的长. ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例17：24. （2015年广东9分）⊙O是△ABC的外接圆，AB是直径，过BC的中点P作⊙O的直径PG交弦BC于点D，连接AG， CP，PB. ‎ ‎（1）如题图1；若D是线段OP的中点，求∠BAC的度数； ‎ ‎（2）如题图2，在DG上取一点k，使DK=DP，连接CK，求证：四边形AGKC是平行四边形； ‎ ‎（3）如题图3，取CP的中点E，连接ED并延长ED交AB于点H，连接PH，求证：PH⊥AB.‎ ‎ ‎ ‎ ‎ ‎ ‎ 例18：26（2015.河北) 平面上，矩形ABCD与直径为QP的半圆K如图15－1摆放，分别延长DA和QP交于点O，且∠DOQ=60°，OQ=OD=3，OP=2，OA=AB=1，让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α（0≤α≤60）. ‎ 发现：(1)当α=0°，即初始位置时，点P 直线AB上. (填“在”或“不在”)， 求当α是多少时，OQ经过点B？ ‎ ‎ (2)在OQ旋转过程中，简要说明α是多少时，点P，A间的距离最小？并指出这个最小值； ‎ ‎ (3)如图15－2，当点P恰好落在BC边上时，求α及S阴影. ‎ 拓展：如图15－3，当线段OQ与CB边交于点M，与BA边交于点N时，设BM=x(x>0)，用含x的代数式表示BN的长，并求x的取值范围. ‎ 探究：当半圆K与矩形ABCD的边相切时，求sinα的值.‎ ‎ ‎ ‎ ‎ ‎ ‎ 例19：23.(2015.陕西) 如图，AB是⊙O的直径，AC是⊙O的弦，过点B作⊙O的切线DE，与AC的延长线交于点D，作AE⊥AC交DE于点E． ‎ ‎ (1)求证：∠BAD=∠E； ‎ ‎ (2)若⊙O的半径为5，AC=8，求BE的长． ‎ ‎ ‎ ‎ ‎ 例20：25. (2015.陕西) 如图，在每一个四边形ABCD中，均有AD∥BC，CD⊥BC，∠ABC=60∘，AD=8，BC=12． ‎ ‎(1)如图 1，点M是四边形ABCD边AD上的一点，则△BMC的面积为 ； ‎ ‎(2)如图 2，点N是四边形ABCD边AD上的任意一点，请你求出△BNC周长的最小值； ‎ ‎ (3)如图 3，在四边形ABCD的边AD上，是否存在一点P，使得cos∠BPC的值最小？若存在，求出此时cos∠BPC的值；若不存在，请说明理由．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例21：23.(2015.安徽) 如图1，在四边形ABCD中，点E、F分别是AB、CD的中点，过点E作AB的垂线，过 点F作CD的垂线，两垂线交于点G，连接AG、BG、CG、DG，且∠AGD＝∠BGC．‎ ‎ (1)求证：AD＝BC；‎ (2) 求证：△AGD∽△EGF；‎ (3) 如图2，若AD、BC所在直线互相垂直，求 AD/EF的值．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例22：22（2015.河南）如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE. 将△EDC绕点C按顺时针方向旋转，记旋转角为α. ‎ （1） 问题发现 ‎ ‎① 当α=0°时，AE/BD=_____________； ‎ ‎② 当α=180°时，AE/BD=__________‎ ‎ （2）拓展探究 ‎ ‎ 试判断：当0°≤α＜360°时，AE/BD的大小有无变化？请仅就图2的情况给出证明. ‎ ‎（3）问题解决 ‎ ‎ 当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长.‎ ‎ ‎ ‎ ‎ ‎ ‎ 例23：21（2015.黄冈）已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O 交AB 于点M，交BC 于点N，连接AN,过点C 的切线交AB 的延长线于点P. ‎ ‎（1）求证：∠BCP=∠BAN; ‎ ‎（2）求证：AM/MN=CB/BP ‎ ‎ ‎ ‎ ‎ ‎ 例24：23．（2015•山西）综合与实践：制作无盖盒子 ‎ 任务一：如图1，有一块矩形纸板，长是宽的2倍，要将其四角各剪去一个正方形，折成高为4cm，容积为616cm3‎ 的无盖长方体盒子（纸板厚度忽略不计）． ‎ （1） 请在图1的矩形纸板中画出示意图，用实线表示剪切线，虚线表示折痕． ‎ （2） 请求出这块矩形纸板的长和宽． ‎ 任务二：图2是一个高为4cm的无盖的五棱柱盒子（直棱柱），图3是其底面，在五边形ABCDE中，BC=12cm，AB=DC=6cm，∠ABC=∠BCD=120°，∠EAB=∠EDC=90°． （1）试判断图3中AE与DE的数量关系，并加以证明． ‎ （2） 图2中的五棱柱盒子可按图4所示的示意图，将矩形纸板剪切折合而成，那么这个矩形纸板的长和宽至少各为多少cm？请直接写出结果（图中实线表示剪切线，虚线表示折痕．纸板厚度及剪切接缝处损耗忽略不计）． ‎ ‎ ‎ ‎ ‎ 例25：25．（2015•吉林）两个三角板ABC，DEF，按如图所示的位置摆放，点B与点D重合，边AB与边DE在同一条直线上（假设图形中所有的点，线都在同一平面内）．其中，∠C=∠DEF=90°，∠ABC=∠F=30°，AC=DE=6cm．现固定三角板DEF，将三角板ABC沿射线DE方向平移，当点C落在边EF上时停止运动．设三角板平移的距离为x（cm），两个三角板重叠部分的面积为y（cm2）． ‎ ‎（1）当点C落在边EF上时，x= cm； ‎ ‎（2）求y关于x的函数解析式，并写出自变量x的取值范围； ‎ ‎（3）设边BC的中点为点M，边DF的中点为点N．直接写出在三角板平移过程中，点M与点N之间距离的最小值．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例26：27．（2015•南通）如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上． ‎ ‎（1）求证：PQ∥AB； ‎ ‎（2）若点D在∠BAC的平分线上，求CP的长； ‎ ‎（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．‎ ‎ ‎ ‎ ‎ 例27：23．（2015•潍坊）如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE． ‎ ‎（1）求证：DE⊥AG； ‎ ‎（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．‎ ‎ ①在旋转过程中，当∠OAG′是直角时，求α的度数； ‎ ‎②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例28：24（2015•温州）如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O．点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF=CD，以DE，DF为邻边作矩形DEGF．设AQ=3x． ‎ ‎（1）用关于x的代数式表示BQ，DF． ‎ ‎（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长． ‎ ‎（3）在点P的整个运动过程中，‎ ‎ ①当AP为何值时，矩形DEGF是正方形？ ‎ ‎②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）‎ ‎ ‎ ‎ ‎ ‎ ‎ 例29：24（2015•呼和浩特）如图，⊙O是△ABC的外接圆，P是⊙O外的一点，AM是⊙O的直径，∠PAC=∠ABC ‎ （1） 求证：PA是⊙O的切线； ‎ （2） ‎（2）连接PB与AC交于点D，与⊙O交于点E，F为BD上的一点，若M为弧BC的中点，且∠DCF=∠P，求证：BD/D=FD/ED=CD/AD．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例30：23 （2015.海南）如图 9-1，菱形 ABCD 中，点 P 是 CD 的中点，∠BCD = 60°，射线 AP 交 BC 的延长线于点 E，射线 BP 交 DE 于点 K，点 O 是线段 BK 的中点． ‎ （1） 求证：△ADP≌△ECP； ‎ （2） 若 BP = n·PK，试求出 n 的值； ‎ ‎（3）作 BM⊥AE 于点 M，作 KN⊥AE 于点 N，连结 MO、NO，如图 9-2 所示． 请证明 ‎△MON 是等腰三角形，并直接写出∠MON 的度数．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例31：25（2015.南宁）如图14，AB是⊙O的直径，C、G是⊙O上两点，且AC = CG，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F. ‎ （1） 求证：CD是⊙O的切线. ‎ （2） 若OF/FD=2/3,求∠E的度数. ‎ （2） 连接AD，在（2）的条件下，若CD=3，求AD的长 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例32：25（2015.贵阳）如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3． ‎ ‎（1）求MP的值；（4分） ‎ ‎（2）在AB边上有一个动点F，且不与点A，B重合． 当AF等于多少时，△MEF的周长最小？（4分） ‎ ‎（3）若点G，Q是AB边上的两个动点，且不与 点A，B重合，GQ=2．当四边 形MEQG的周长最小时， 求最小周长值.（计算结果保留根号）（4分） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例33：22（2015•乌鲁木齐）如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DE⊥AD且与AC的延长线交于点E． ‎ ‎（1）求证：DC=DE； ‎ ‎（2）若tan∠CAB=1/2，AB=3，求BD的长．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例34：27（2015.兰州）如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D。以AB上一点O为圆心作⊙O，使⊙O经过点A和点D。 ‎ （1） 判断直线BC与⊙O的位置关系，并说明理由； ‎ （2） 若AC=3，∠B=30°， ‎ ‎①求⊙O的半径； ‎ ‎②设⊙O与AB边的另一个交点为E，求线段BD，BE与劣弧DE所围成的阴影部分的面积（结果保留根号和）。‎ ‎ ‎ ‎ ‎ ‎ ‎ 例35：22（2015.昆明）如图，AH是⊙O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为半径OH上一点，点E、F分别在矩形ABCD的边BC和CD上。 ‎ （1） 求证：直线FG是⊙O的切线； ‎ （2） 若CD＝10，EB＝5,求⊙O的直径．‎ ‎ ‎ ‎ ‎ 例36：25（2015•包头）如图，四边形ABCD中，AD∥BC，∠A=90°，AD=1厘米，AB=3厘米，BC=5厘米，动点P从点B出发以1厘米/秒的速度沿BC方向运动，动点Q从点C出发以2厘米/秒的速度沿CD方向运动，P，Q两点同时出发，当点Q到达点D时停止运动，点P也随之停止，设运动时间为t秒（t＞0）． ‎ ‎（1）求线段CD的长； ‎ ‎（2）t为何值时，线段PQ将四边形ABCD的面积分为1：2两部分？ ‎ ‎（3）伴随P，Q两点的运动，线段PQ的垂直平分线为l．‎ ‎①t为何值时，l经过点C？ ‎ ‎②求当l经过点D时t的值，并求出此时刻线段PQ的长．‎ ‎ ‎ 例37：25（2015.宁夏）如图，是一副学生用的三角板，在△ABC 中，∠C=90°, ∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°, ∠A1=45°，∠B1=45°，且A1B1= CB ．若将边A1C1与边CA重合，其中点A1 与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为M, 设AC=a． ‎ （1） 计算A1C1的长； ‎ （2） 当α=30°时，证明：B1C1∥AB； ‎ （3） 若a=+，当α=45°时，计算两个三角板重叠部分图形的面积； ‎ （4） 当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积．‎ ‎（参考数据：sin15°=(－)/4-，cos15°=(+)/4+，tan15°=2－ sin75°=(+)/4‎ ‎ , cos75°= (－)/4- , tan75°=2+ ）‎ ‎ ‎ ‎ ‎ ‎ ‎ 例38：26（2015.青海）如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D． ‎ ‎（1）求证：AM=AC； ‎ ‎（2）若AC=3，求MC的长．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例39：25．（2015.山东临沂）如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE. （1）请判断：AF与BE的数量关系是 ，位置关系是 ； ‎ ‎（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC，第（1）问中的结论是否仍然成立?请作出判断并给予证明； ‎ ‎（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断. ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例40：28．（2015.湖南衡阳）如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥OA，交BO于点N，连接ND、BM，设OP=t． ‎ ‎（1）求点M的坐标（用含t的代数式表示）． ‎ ‎（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由． ‎ ‎（3）当t为何值时，四边形BNDM的面积最小．‎ ‎ ‎ ‎ ‎ ‎ ‎ 例41：25．(2015.湖北襄阳)如图，AB是⊙O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，PB∶PC＝1∶2. ‎ ‎（1）求证：AC平分∠BAD； ‎ ‎（2）探究线段PB，AB之间的数量关系，并说明理由； ‎ ‎（3）若AD＝3，求△ABC的面积.‎ ‎ ‎ 例42：22.（2015.武汉）已知锐角△ABC中，边BC长为12，高AD长为8 (1) 如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K ‎ ① 求EF/AK的值 ‎ ② 设EH＝x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值 ‎ (2) ‎ 若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长 ‎ ‎ ‎ ‎ ‎ ‎ ‎23．（2015.武汉）如图，△ABC中，点E、P在边AB上，且AE＝BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3 ‎ ‎(1) 求证：EF＋PQ＝BC ‎ (2) 若S1＋S3＝S2，求PE/AE的值 ‎ (3) 若S3－S1＝S2，直接写出PE/AE的值 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎