初三数学中考必考题

初三数学中考必考题

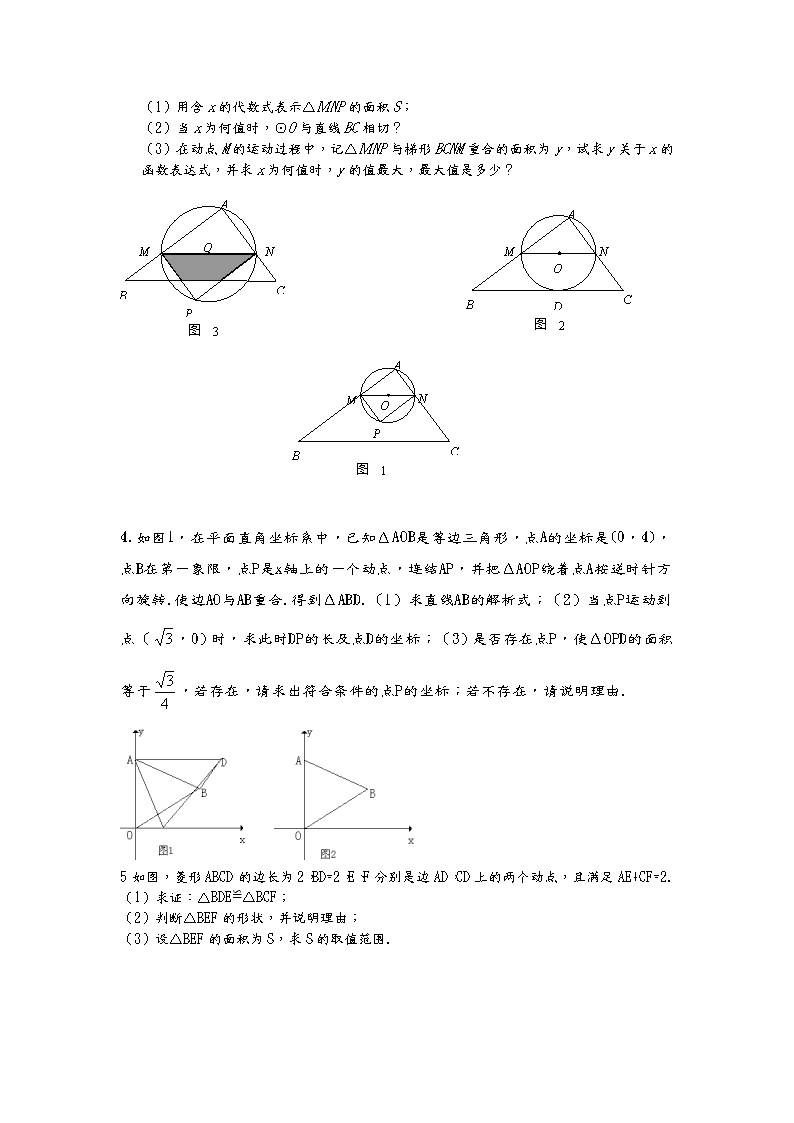
初三数学中考必考题 ‎1.‎ 已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A（-1，0）、B（0，3）两点，其顶点为D.‎ （1） 求该抛物线的解析式；‎ （2） 若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积；‎ （3） ‎△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由.‎ ‎（注：抛物线y=ax2+bx+c(a≠0)的顶点坐标为）‎ ‎2. 如图，在中，，，，分别是边的中点，点从点出发沿方向运动，过点作于，过点作交于 ‎，当点与点重合时，点停止运动．设，．‎ ‎（1）求点到的距离的长；‎ ‎（2）求关于的函数关系式（不要求写出自变量的取值范围）；‎ ‎（3）是否存在点，使为等腰三角形？若存在，请求出所有满足要求的的值；若不存在，请说明理由．‎ A B C D E R P H Q ‎3在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x． ‎ ‎（1）用含x的代数式表示△ＭNP的面积S； ‎ ‎（2）当x为何值时，⊙O与直线BC相切？ ‎ ‎（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？‎ A B C M N P 图 3‎ O A B C M N D 图 2‎ O A B C M N P 图 1‎ O ‎4.如图1，在平面直角坐标系中，己知ΔAOB是等边三角形，点A的坐标是(0，4)，点B在第一象限，点P是x轴上的一个动点，连结AP，并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.（1）求直线AB的解析式；（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；（3）是否存在点P，使ΔOPD的面积等于，若存在，请求出符合条件的点P的坐标；若不存在，请说明理由.‎ ‎5如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2.‎ ‎（1）求证：△BDE≌△BCF； ‎ ‎（2）判断△BEF的形状，并说明理由；‎ ‎（3）设△BEF的面积为S，求S的取值范围.‎ ‎6如图，抛物线交轴于A、B两点，交轴于M点.抛物线向右平移2个单位后得到抛物线，交轴于C、D两点.‎ ‎（1）求抛物线对应的函数表达式；‎ ‎（2）抛物线或在轴上方的部分是否存在点N，使以A，C，M，N为顶点的四边形是平行四边形.若存在，求出点N的坐标；若不存在，请说明理由；‎ ‎（3）若点P是抛物线上的一个动点（P不与点A、B重合），那么点P关于原点的对称点Q是否在抛物线上，请说明理由.‎ ‎7.如图，在梯形ABCD中，AB∥CD，AB＝7，CD＝1，AD＝BC＝5．点M，N分别在边AD，BC上运动，并保持MN∥AB，ME⊥AB，NF⊥AB，垂足分别为E，F．‎ ‎（1）求梯形ABCD的面积； ‎ ‎（2）求四边形MEFN面积的最大值． ‎ ‎（3）试判断四边形MEFN能否为正方形，若能，‎ 求出正方形MEFN的面积；若不能，请说明理由． ‎ C D A B E F N M ‎8.如图，点A（m，m＋1），B（m＋3，m－1）都在反比例函数的图象上． ‎ x O y A B ‎（1）求m，k的值； ‎ ‎（2）如果M为x轴上一点，N为y轴上一点， ‎ 以点A，B，M，N为顶点的四边形是平行四边形， ‎ 友情提示：本大题第（1）小题4分，第（2）小题7分．对完成第（2）小题有困难的同学可以做下面的（3）选做题．选做题2分，所得分数计入总分．但第（2）、（3）小题都做的，第（3）小题的得分不重复计入总分．　 ‎ 试求直线MN的函数表达式． ‎ x O y ‎1‎ ‎2‎ ‎3‎ ‎1‎ Q P ‎2‎ P1‎ Q1‎ ‎（3）选做题：在平面直角坐标系中，点P的坐标 为（5，0），点Q的坐标为（0，3），把线段PQ向右平 移4个单位，然后再向上平移2个单位，得到线段P1Q1，‎ 则点P1的坐标为 ，点Q1的坐标为 ．‎ ‎9.如图16，在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过三点．‎ ‎（1）求过三点抛物线的解析式并求出顶点的坐标；‎ ‎（2）在抛物线上是否存在点，使为直角三角形，若存在，直接写出点坐标；若不存在，请说明理由；‎ ‎（3）试探究在直线上是否存在一点，使得的周长最小，若存在，求出点的坐标；若不存在，请说明理由．‎ A O x y B F C 图16‎ ‎10.如图所示，在平面直角坐标系中，矩形的边在轴的负半轴上，边在轴的正半轴上，且，，矩形绕点按顺时针方向旋转后得到矩形．点的对应点为点，点的对应点为点，点的对应点为点，抛物线过点．‎ ‎（1）判断点是否在轴上，并说明理由；‎ ‎（2）求抛物线的函数表达式；‎ ‎（3）在轴的上方是否存在点，点，使以点为顶点的平行四边形的面积是矩形面积的2倍，且点在抛物线上，若存在，请求出点，点的坐标；若不存在，请说明理由．‎ y x O D E C F A B ‎11.已知：如图14，抛物线与轴交于点，点，与直线相交于点，点，直线与轴交于点．‎ ‎（1）写出直线的解析式．‎ ‎（2）求的面积．‎ ‎（3）若点在线段上以每秒1个单位长度的速度从向运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？‎ ‎12.在平面直角坐标系中△ABC的边AB在x轴上，且OA>OB,以AB为直径的圆过点C若C的坐标为(0,2),AB=5, A,B两点的横坐标XA,XB是关于X的方程的两根:‎ (1) 求m，n的值 (2) 若∠ACB的平分线所在的直线交x轴于点D，试求直线对应的一次函数的解析式 (3) 过点D任作一直线分别交射线CA，CB（点C除外）于点M，N，则的值是否为定值，若是，求出定值，若不是，请说明理由 A C O B N D M L`‎ ‎13.已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A（-1，0）、B（0，3）两点，其顶点为D.‎ ‎(1)求该抛物线的解析式；‎ ‎(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积；‎ ‎(3)△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由.‎ ‎（注：抛物线y=ax2+bx+c(a≠0)的顶点坐标为）‎ ‎14.已知抛物线，‎ ‎（Ⅰ）若，，求该抛物线与轴公共点的坐标；‎ ‎（Ⅱ）若，且当时，抛物线与轴有且只有一个公共点，求的取值范围；‎ ‎（Ⅲ）若，且时，对应的；时，对应的，试判断当 时，抛物线与轴是否有公共点？若有，请证明你的结论；若没有，阐述理由．‎ ‎15.已知：如图①，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：‎ ‎（1）当t为何值时，PQ∥BC？‎ ‎（2）设△AQP的面积为y（），求y与t之间的函数关系式；‎ ‎（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；‎ ‎（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．‎ 图②‎ A Q C P B 图①‎ A Q C P B ‎16.已知双曲线与直线相交于A、B两点.第一象限上的点M（m，n）（在A点左侧）是双曲线上的动点.过点B作BD∥y轴于点D.过N（0，－n）作NC∥x轴交双曲线于点E，交BD于点C.‎ ‎（1）若点D坐标是（－8，0），求A、B两点坐标及k的值.‎ ‎（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式.‎ ‎（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA＝pMP，MB＝qMQ，求p－q的值.‎ 压轴题答案 ‎1. 解：（ 1）由已知得：解得 c=3,b=2‎ ‎∴抛物线的线的解析式为 ‎(2)由顶点坐标公式得顶点坐标为（1，4）‎ 所以对称轴为x=1,A,E关于x=1对称，所以E(3,0)‎ 设对称轴与x轴的交点为F 所以四边形ABDE的面积=‎ ‎=‎ ‎=‎ ‎=9‎ ‎（3）相似 如图，BD=‎ BE=‎ DE=‎ 所以, 即： ,所以是直角三角形 所以,且,‎ 所以.‎ ‎2 解：（1），，，．‎ 点为中点，．‎ ‎，．‎ ‎，‎ ‎，．‎ ‎（2），．‎ ‎，，‎ ‎，，‎ 即关于的函数关系式为：．‎ ‎（3）存在，分三种情况：‎ A B C D E R P H Q M ‎2‎ ‎1‎ ‎①当时，过点作于，则．‎ ‎，，‎ ‎．‎ ‎，，‎ A B C D E R P H Q ‎，．‎ A B C D E R P H Q ‎②当时，，‎ ‎．‎ ‎③当时，则为中垂线上的点，‎ 于是点为的中点，‎ ‎．‎ ‎，‎ A B C M N P 图 1‎ O ‎，．‎ 综上所述，当为或6或时，为等腰三角形．‎ ‎3解：（1）∵MN∥BC，∴∠AMN=∠B，∠ANM＝∠C． ‎ ‎ ∴ △AMN ∽ △ABC．‎ ‎∴ ，即．‎ ‎∴ AN＝x． ……………2分 ‎∴ =．（0＜＜4） ……………3分 A B C M N D 图 2‎ O Q ‎（2）如图2，设直线BC与⊙O相切于点D，连结AO，OD，则AO =OD =MN．‎ 在Rt△ABC中，BC ＝=5．‎ ‎ 由（1）知 △AMN ∽ △ABC． ‎ ‎∴ ，即． ‎ ‎∴ ，‎ ‎∴ ． …………………5分 过M点作MQ⊥BC 于Q，则． ‎ 在Rt△BMQ与Rt△BCA中，∠B是公共角，‎ ‎∴ △BMQ∽△BCA．‎ ‎∴ ．‎ ‎∴ ，． ‎ ‎∴ x＝． ‎ ‎∴ 当x＝时，⊙O与直线BC相切．…………………………………7分 A B C M N P 图 3‎ O ‎（3）随点M的运动，当P点落在直线BC上时，连结AP，则O点为AP的中点．‎ ‎∵ MN∥BC，∴ ∠AMN=∠B，∠AOM＝∠APC．‎ ‎∴ △AMO ∽ △ABP． ‎ ‎∴ ． AM＝MB＝2． ‎ 故以下分两种情况讨论： ‎ ① 当0＜≤2时，． ‎ A B C M N P 图 4‎ O E F ‎∴ 当＝2时， ……………………………………8分 ② 当2＜＜4时，设PM，PN分别交BC于E，F．‎ ‎∵ 四边形AMPN是矩形， ‎ ‎∴ PN∥AM，PN＝AM＝x． ‎ 又∵ MN∥BC， ‎ ‎∴ 四边形MBFN是平行四边形． ‎ ‎∴ FN＝BM＝4－x． ‎ ‎∴ ． ‎ 又△PEF ∽ △ACB． ‎ ‎∴ ．‎ ‎∴ ． ……………………………………………… 9分 ‎＝．……………………10分 当2＜＜4时，． ‎ ‎∴ 当时，满足2＜＜4，． ……………………11分 综上所述，当时，值最大，最大值是2． …………………………12分 ‎4 解：（1）作BE⊥OA，∴ΔAOB是等边三角形∴BE=OB·sin60o=，∴B(,2)‎ ‎∵A(0,4),设AB的解析式为,所以,解得,‎ 以直线AB的解析式为 ‎（2）由旋转知，AP=AD, ∠PAD=60o,‎ ‎∴ΔAPD是等边三角形，PD=PA=‎ 如图，作BE⊥AO,DH⊥OA,GB⊥DH,显然ΔGBD中∠GBD=30°‎ ‎∴GD=BD=,DH=GH+GD=+=,‎ ‎∴GB=BD=,OH=OE+HE=OE+BG=‎ ‎∴D(,)‎ ‎(3)设OP=x,则由（2）可得D()若ΔOPD的面积为：‎ 解得：所以P(,0)‎ ‎5‎ ‎6‎ ‎7解：（1）分别过D，C两点作DG⊥AB于点G，CH⊥AB于点H． ……………1分 ‎∵ AB∥CD， ‎ ‎∴ DG＝CH，DG∥CH． ‎ ‎∴ 四边形DGHC为矩形，GH＝CD＝1． ‎ C D A B E F N M G H ‎∵ DG＝CH，AD＝BC，∠AGD＝∠BHC＝90°，‎ ‎∴ △AGD≌△BHC（HL）． ‎ ‎∴ AG＝BH＝＝3． ………2分 ‎ ‎∵ 在Rt△AGD中，AG＝3，AD＝5， ‎ ‎∴ DG＝4． ‎ ‎∴ ． ………………………………………………3分 C D A B E F N M G H ‎（2）∵ MN∥AB，ME⊥AB，NF⊥AB， ‎ ‎∴ ME＝NF，ME∥NF． ‎ ‎∴ 四边形MEFN为矩形． ‎ ‎∵ AB∥CD，AD＝BC， ‎ ‎∴ ∠A＝∠B． ‎ ‎∵ ME＝NF，∠MEA＝∠NFB＝90°， ‎ ‎∴ △MEA≌△NFB（AAS）．‎ ‎∴ AE＝BF． ……………………4分 ‎ 设AE＝x，则EF＝7－2x． ……………5分 ‎ ‎∵ ∠A＝∠A，∠MEA＝∠DGA＝90°， ‎ ‎∴ △MEA∽△DGA．‎ ‎∴ ．‎ ‎∴ ME＝． …………………………………………………………6分 ‎∴ ． ……………………8分 当x＝时，ME＝＜4，∴四边形MEFN面积的最大值为．……………9分 ‎（3）能． ……………………………………………………………………10分 由（2）可知，设AE＝x，则EF＝7－2x，ME＝． ‎ 若四边形MEFN为正方形，则ME＝EF． ‎ ‎ 即 7－2x．解，得 ． ……………………………………………11分 ‎∴ EF＝＜4． ‎ ‎∴ 四边形MEFN能为正方形，其面积为．‎ ‎8解：（1）由题意可知，．‎ 解，得 m＝3． ………………………………3分 ‎ x O y A B M1‎ N1‎ M2‎ N2‎ ‎∴ A（3，4），B（6，2）； ‎ ‎∴ k＝4×3=12． ……………………………4分 ‎ ‎（2）存在两种情况，如图： ‎ ‎①当M点在x轴的正半轴上，N点在y轴的正半轴 上时，设M1点坐标为（x1，0），N1点坐标为（0，y1）． ‎ ‎∵ 四边形AN1M1B为平行四边形，‎ ‎∴ 线段N1M1可看作由线段AB向左平移3个单位，‎ 再向下平移2个单位得到的（也可看作向下平移2个单位，再向左平移3个单位得到的）．‎ 由（1）知A点坐标为（3，4），B点坐标为（6，2）， ‎ ‎∴ N1点坐标为（0，4－2），即N1（0，2）； ………………………………5分 M1点坐标为（6－3，0），即M1（3，0）． ………………………………6分 设直线M1N1的函数表达式为，把x＝3，y＝0代入，解得．‎ ‎∴ 直线M1N1的函数表达式为． ……………………………………8分 ‎②当M点在x轴的负半轴上，N点在y轴的负半轴上时，设M2点坐标为（x2，0），N2点坐标为（0，y2）． ‎ ‎∵ AB∥N1M1，AB∥M2N2，AB＝N1M1，AB＝M2N2，‎ ‎∴ N1M1∥M2N2，N1M1＝M2N2． ‎ ‎∴ 线段M2N2与线段N1M1关于原点O成中心对称． ‎ ‎∴ M2点坐标为（-3，0），N2点坐标为（0，-2）． ………………………9分 设直线M2N2的函数表达式为，把x＝-3，y＝0代入，解得，‎ ‎∴ 直线M2N2的函数表达式为． 　　 ‎ 所以，直线MN的函数表达式为或． ………………11分 ‎（3）选做题：（9，2），（4，5）． ………………………………………………2分 ‎9解：（1）直线与轴交于点，与轴交于点．‎ ‎， 1分 点都在抛物线上，‎ ‎ ‎ 抛物线的解析式为 3分 顶点 4分 ‎（2）存在 5分 ‎ 7分 ‎ 9分 ‎（3）存在 10分 理由：‎ 解法一：‎ 延长到点，使，连接交直线于点，则点就是所求的点．‎ ‎ 11分 A O x y B F C 图9‎ H B M 过点作于点．‎ 点在抛物线上，‎ 在中，，‎ ‎，，‎ 在中，，‎ ‎，， 12分 设直线的解析式为 ‎ 解得 ‎ 13分 ‎ 解得 ‎ 在直线上存在点，使得的周长最小，此时． 14分 解法二：‎ A O x y B F C 图10‎ H M G 过点作的垂线交轴于点，则点为点关于直线的对称点．连接交于点，则点即为所求． 11分 过点作轴于点，则，．‎ ‎，‎ 同方法一可求得．‎ 在中，，，可求得，‎ 为线段的垂直平分线，可证得为等边三角形，‎ 垂直平分．‎ 即点为点关于的对称点． 12分 设直线的解析式为，由题意得 ‎ 解得 ‎ 13分 ‎ 解得 ‎ 在直线上存在点，使得的周长最小，此时． 1‎ ‎10解：（1）点在轴上 1分 理由如下：‎ 连接，如图所示，在中，，，‎ ‎，‎ 由题意可知：‎ 点在轴上，点在轴上． 3分 ‎（2）过点作轴于点 ‎，‎ 在中，，‎ 点在第一象限，‎ 点的坐标为 5分 由（1）知，点在轴的正半轴上 点的坐标为 点的坐标为 6分 抛物线经过点，‎ 由题意，将，代入中得 ‎ 解得 所求抛物线表达式为： 9分 ‎（3）存在符合条件的点，点． 10分 理由如下：矩形的面积 以为顶点的平行四边形面积为．‎ 由题意可知为此平行四边形一边，‎ 又 边上的高为2 11分 依题意设点的坐标为 点在抛物线上 解得，，‎ ‎，‎ 以为顶点的四边形是平行四边形，‎ y x O D E C F A B M ‎，，‎ 当点的坐标为时，‎ 点的坐标分别为，；‎ 当点的坐标为时，‎ 点的坐标分别为，． 14分 ‎（以上答案仅供参考，如有其它做法，可参照给分）‎ ‎11解：（1）在中，令 x y A B C E M D P N O ‎，‎ ‎， 1分 又点在上 的解析式为 2分 ‎（2）由，得 4分 ‎，‎ ‎， 5分 ‎ 6分 ‎（3）过点作于点 ‎ 7分 ‎ 8分 由直线可得：‎ 在中，，，则 ‎， 9分 ‎ 10分 ‎ 11分 此抛物线开口向下，当时，‎ 当点运动2秒时，的面积达到最大，最大为． ‎ ‎12解：‎ ‎(1)m=-5,n=-3‎ ‎ (2)y=x+2‎ ‎(3)是定值.‎ 因为点D为∠ACB的平分线，所以可设点D到边AC,BC的距离均为h，‎ 设△ABC AB边上的高为H,‎ 则利用面积法可得：‎ ‎（CM+CN）h=MN﹒H 又 H=‎ 化简可得 (CM+CN)﹒‎ 故 ‎ ‎13解：（ 1）由已知得：解得 c=3,b=2‎ ‎∴抛物线的线的解析式为 ‎(2)由顶点坐标公式得顶点坐标为（1，4）‎ 所以对称轴为x=1,A,E关于x=1对称，所以E(3,0)‎ 设对称轴与x轴的交点为F 所以四边形ABDE的面积=‎ ‎=‎ ‎=‎ ‎=9‎ ‎（3）相似 如图，BD=‎ BE=‎ DE=‎ 所以, 即： ,所以是直角三角形 所以,且,‎ 所以.‎ ‎14解（Ⅰ）当，时，抛物线为，‎ 方程的两个根为，． ‎ ‎∴该抛物线与轴公共点的坐标是和． 2分 ‎（Ⅱ）当时，抛物线为，且与轴有公共点．‎ 对于方程，判别式≥0，有≤． 3分 ‎①当时，由方程，解得．‎ 此时抛物线为与轴只有一个公共点． 4分 ‎②当时， ‎ 时，，‎ 时，．‎ 由已知时，该抛物线与轴有且只有一个公共点，考虑其对称轴为，‎ 应有 即 解得．‎ 综上，或． 6分 ‎（Ⅲ）对于二次函数，‎ 由已知时，；时，，‎ 又，∴．‎ 于是．而，∴，即．‎ ‎∴． 7分 ‎∵关于的一元二次方程的判别式 ‎， ‎ x ‎∴抛物线与轴有两个公共点，顶点在轴下方． 8分 又该抛物线的对称轴，‎ 由，，，‎ 得，‎ ‎∴．‎ 又由已知时，；时，，观察图象，‎ 可知在范围内，该抛物线与轴有两个公共点． 10分 ‎15 解：（1）由题意：BP＝tcm，AQ＝2tcm，则CQ＝(4－2t)cm，‎ ‎∵∠C＝90°，AC＝4cm，BC＝3cm，∴AB＝5cm ‎∴AP＝（5－t）cm，‎ ‎∵PQ∥BC，∴△APQ∽△ABC，‎ ‎∴AP∶AB＝AQ∶AC，即（5－t）∶5＝2t∶4，解得：t＝‎ ‎∴当t为秒时，PQ∥BC ‎………………2分 ‎（2）过点Q作QD⊥AB于点D，则易证△AQD∽△ABC ‎∴AQ∶QD＝AB∶BC ‎∴2t∶DQ＝5∶3，∴DQ＝‎ ‎∴△APQ的面积：×AP×QD＝（5－t）×‎ ‎∴y与t之间的函数关系式为：y＝‎ ‎………………5分 ‎（3）由题意：‎ ‎ 当面积被平分时有：＝××3×4，解得：t＝‎ ‎ 当周长被平分时：（5－t）＋2t＝t＋（4－2t）＋3，解得：t＝1‎ ‎∴不存在这样t的值 ‎………………8分 ‎（4）过点P作PE⊥BC于E ‎ 易证：△PAE∽△ABC，当PE＝QC时，△PQC为等腰三角形，此时△QCP′为菱形 ‎∵△PAE∽△ABC，∴PE∶PB＝AC∶AB，∴PE∶t＝4∶5，解得：PE＝‎ ‎∵QC＝4－2t，∴2×＝4－2t,解得：t＝‎ ‎∴当t＝时，四边形PQP′C为菱形 此时，PE＝，BE＝，∴CE＝‎ ‎………………10分 在Rt△CPE中，根据勾股定理可知：PC＝＝＝‎ ‎∴此菱形的边长为cm ………………12分 ‎16 解：（1）∵D（－8，0），∴B点的横坐标为－8，代入中，得y＝－2.‎ ‎∴B点坐标为（－8，－2）.而A、B两点关于原点对称，∴A（8，2）‎ 从而k＝8×2＝16‎ ‎（2）∵N（0，－n），B是CD的中点，A，B，M，E四点均在双曲线上,‎ ‎∴mn＝k，B（－2m，－），C（－2m，－n），E（－m，－n）‎ ‎＝2mn＝2k，＝mn＝k，＝mn＝k.‎ ‎∴＝――＝k.∴k＝4.‎ 由直线及双曲线，得A（4，1），B（－4，－1）‎ ‎∴C（－4，－2），M（2，2）‎ 设直线CM的解析式是，由C、M两点在这条直线上，得 ‎，解得a＝b＝‎ ‎∴直线CM的解析式是y＝x＋.‎ ‎（3）如图，分别作AA1⊥x轴，MM1⊥x轴，垂足分别为A1，M1‎ 设A点的横坐标为a，则B点的横坐标为－a.于是，‎ 同理 ‎∴p－q＝－＝－2‎