广东省各市中考数学压轴题及答案

广东省各市中考数学压轴题及答案

‎2010年广东省各市中考数学压轴题及答案 ‎1.（2010广东中山）．已知两个全等的直角三角形纸片ABC、DEF，如图（1）放置，点B、D重合，点F在BC上，AB与EF交于点G。∠C=∠EFB=90º，∠E=∠ABC=30º，AB=DE=4。‎ ‎（1）求证：△EGB是等腰三角形；‎ 第20题图（1）‎ A B C E F F B（D）‎ G G A C E D 第20题图（2）‎ ‎（2）若纸片DEF不动，问△ABC绕点F逆时针旋转最小_____度时，四边形ACDE成为以ED为底的梯形（如图（2）），求此梯形的高。‎ ‎2.（2010广东中山）阅读下列材料：‎ ‎ 1×2 = ×(1×2×3－0×1×2)， 2×3 = ×(2×3×4－1×2×3)， 3×4 = ×(3×4×5－2×3×4)，‎ ‎ 由以上三个等式相加，可得1×2＋2×3＋3×4 = ×3×4×5 = 20。‎ 读完以上材料，请你计算下列各题：‎ ‎（1）1×2＋2×3＋3×4＋···＋10×11（写出过程）；（2）1×2＋2×3＋3×4＋···＋n×(n＋1) = _________； （3）1×2×3＋2×3×4＋3×4×5＋···＋7×8×9 = _________。‎ ‎3.（2010广东中山）如图（1），（2）所示，矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2。动点M、N分别 从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），‎ 当动点N运动到点A时，M、N两点同时停止运动。连接FM、FN，当F、N、M不在同一直线时，‎ 可得△FMN，过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒，M、N运动的时间为x秒。试解答下列问题：‎ ‎（1）说明△FMN∽△QWP；‎ ‎（2）设0≤x≤4（即M从D到A运动的时间段）。试问x为何值时，△PQW为直角三角形？‎ 当x在何范围时，△PQW不为直角三角形？‎ 第22题图（2）‎ A B C D F M N W P Q ‎（3）问当x为何值时，线段MN最短？求此时MN的值。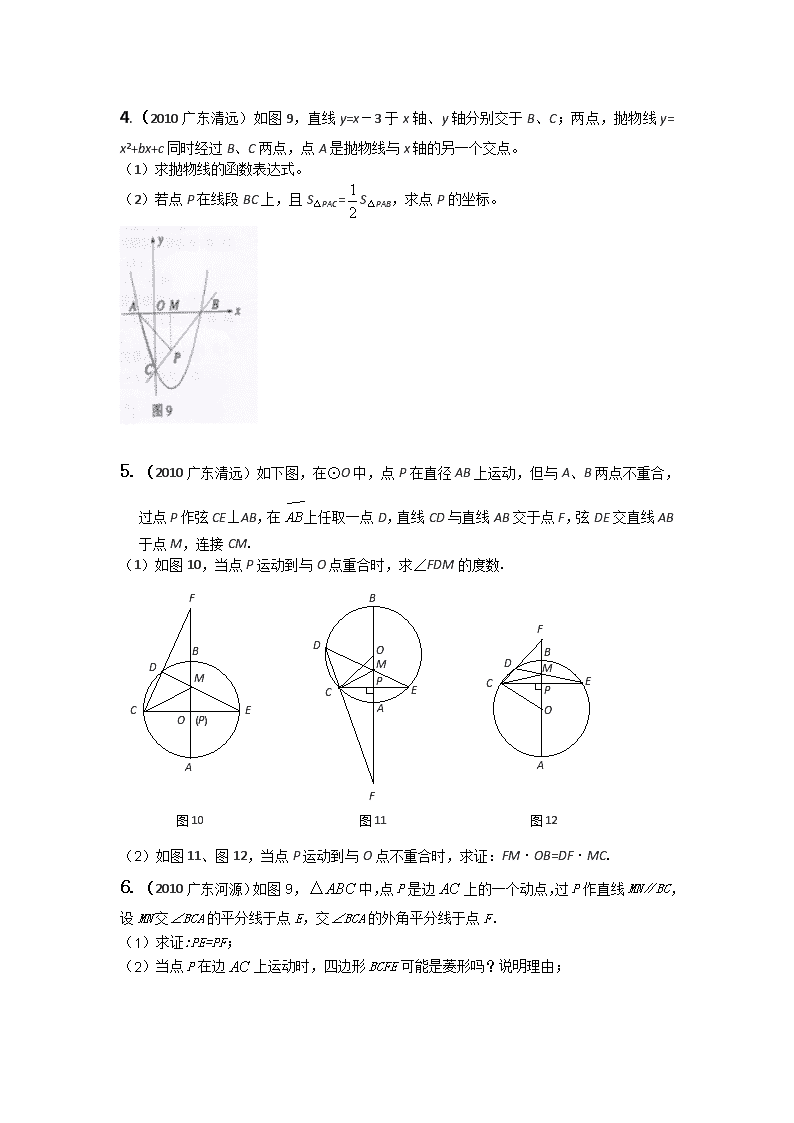‎ 第22题图（1）‎ A B M C F D N W P Q ‎4.（2010广东清远）如图9，直线y=x－3于x轴、y轴分别交于B、C；两点，抛物线y= x2+bx+c同时经过B、C两点，点A是抛物线与x轴的另一个交点。‎ ‎（1）求抛物线的函数表达式。‎ ‎（2）若点P在线段BC上，且S△PAC=S△PAB，求点P的坐标。‎ ‎5.（2010广东清远）如下图，在⊙O中，点P在直径AB上运动，但与A、B两点不重合，过点P作弦CE⊥AB，在上任取一点D，直线CD与直线AB交于点F，弦DE交直线AB于点M，连接CM.‎ ‎（1）如图10，当点P运动到与O点重合时，求∠FDM的度数.‎ 图10 图11 图12‎ C A B ‎(P)‎ E O M F D C A B P E O F D M O C A B P E F D M （2） 如图11、图12，当点P运动到与O点不重合时，求证：FM·OB=DF·MC.‎ ‎6.（2010广东河源）如图9，中，点P是边上的一个动点，过P作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．‎ ‎（1）求证:PE=PF；‎ ‎（2）当点P在边上运动时，四边形BCFE可能是菱形吗？说明理由；‎ ‎（3）若在AC边上存在点P,使四边形AECF是正方形,且.求此时∠A的大小.‎ ‎7.（2010广东河源）如图10，直角梯形OABC中，OC∥AB，C（0，3），B（4，1），以BC为直径的圆交轴于E，D两点（D点在E点右方）.‎ ‎（1）求点E,D 的坐标;‎ ‎（2）求过B,C,D三点的抛物线的函数关系式；‎ ‎(3)过B,C,D三点的抛物线上是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标. ‎ ‎2‎ ‎4‎ ‎4‎ ‎2‎ O y x 图10‎ ‎8.（肇庆市2010）(8分)如图是反比例函数y＝的图象的一支，根据图象回答下列问题：‎ ‎(1)图象的另一支在哪个象限？常数n的取值范围是什么？‎ ‎(2)若函数图象经过点(3，1)，求n的值；‎ ‎(3)在这个函数图象的某一支上任取点A(a1，b1)和点B(a2，b2)，如果a1＜a2，试比较b1和b2的大小．‎ A B O C P E F ‎9.（肇庆市2010）如图，AB是⊙O的直径，AC切⊙O于点A，且AC＝AB，CO交⊙O于点P，CO的延长线交⊙O于点F，BP的延长线交AC于点E，连接AP、AF．‎ 求证：(1)AF∥BE；(2)△ACP∽△FCA；(3)CP＝AE．‎ ‎10.（肇庆市2010）已知二次函数y＝x2＋bx＋c＋1的图象过点P(2，1)．‎ ‎(1)求证：c＝―2b―4；‎ ‎(2)求bc的最大值；‎ ‎(3)若二次函数的图象与x轴交于点A(x1，0)、B(x2，0)，△ABP的面积是，求b的值．‎ ‎11.（2010.广东茂名）‎ ‎12.2010.广东茂名）‎ ‎ ‎ ‎13.(2010广东湛江）病人按规定的剂量服用某药物，测得服药后2小时，每毫升血液中含药量达到最大值为4毫克．已知服药后，2小时前每毫升血液中含药量y(毫克)与时间x(小时)成正比例；2小时后y与x成反比例(如图所示)．根据以上信息解答下列问题：‎ ‎(1)求当0≤x≤2时，y与x的函数关系式；‎ ‎(2)求当x＞2时，y与x的函数关系式；‎ ‎(3)如果每毫升血液中含药量不低于2毫克时治疗有效，‎ O y/毫克 x/小时 ‎2‎ ‎4‎ 则那么服药一次，治疗疾病的有效时间是多长？‎ ‎14.(2010广东湛江）如图，在平面直角坐标系中，点B的坐标为(－3，－4)，线段OB绕原点逆时针旋转后与x轴的正半轴重合，点B的对应点为点A．‎ ‎(1)直接写出点A的坐标，并求出经过A、O、B三点的抛物线的解析式；‎ ‎(2)在抛物线的对称轴上是否存在点C，使BC＋OC的值最小？若存在，求出点C的坐标；若不存在，请说明理由；‎ A O B y x ‎(3)点P是抛物线上的一个动点，且在x轴的上方，当点P运动到什么位置时，△PAB的面积最大？求出此时点P的坐标和△PAB的最大面积．‎ ‎15.（2010广东佛山）新知识一般有两类：第一类是不依赖于其他知识的新知识，如“数”、“字母表示数”这样的初始性的知识；第二类是在某些就只是的基础上进行联系、拓广等方式产生的知识，大多数知识是这样的知识。‎ ‎（1）多项式乘以多项式的法则，是第几类知识？‎ ‎（2）在多项式乘以多项式之前，你已拥有的有关知识是哪些？（写出三条即可）‎ ‎（3）请你用已拥有的有关知识，通过数和形两个方面说明多项式乘以多项式的法则时如何获得的?(用（a+b）（c+d）来说明)‎ ‎16.（2010广东佛山）一般来说，依据数学研究对象本质属性的相同点和差异点，将数学对象分为不同种类的数学思想叫做“分类”的思想；将事物进行分类，然后对划分的每一类分别进行研究和求解的方法叫做“分类讨论”的方法。请依据分类的思想和分类讨论的方法解决下列问题：‎ 如图，在△ABC中，∠ACB＞∠ABC。‎ （1） 若∠BAC是锐角，请探索在直线AB上有多少个点D，能保证△ACD～△ABC（不包括全等）？‎ （2） 请对∠BAC进行恰当的分类，直接写出每一类在直线AB上能保证△ACD～△ABC(不包括全等)的点D的个数。‎ ‎17.（2010广东广州）如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．‎ ‎（1）求弦AB的长；‎ ‎（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；‎ ‎（3）记△ABC的面积为S，若＝4，求△ABC的周长.‎ C P D O B A E ‎18.（2010广东广州）如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线＝－＋交折线OAB于点E．‎ ‎（1）记△ODE的面积为S，求S与的函数关系式；‎ ‎（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B1C1，试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.‎ C D B A E O ‎19.（2010广东深圳）如图9，抛物线y＝ax2＋c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（－2,0），B（－1, －3）．‎ ‎ （1）求抛物线的解析式；（3分）‎ ‎（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；（2分）‎ ‎（3）在第（2）问的结论下，抛物线上的点P使S△PAD＝4S△ABM成立，求点P的坐标．（4分）‎x y C B ‎_‎ D ‎_‎ A O 图9‎ ‎20.（2010广东深圳）以点M（－1,0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－ x－ 与⊙M相切于点H，交x轴于点E，交y轴于点F．‎ ‎ （1）请直接写出OE、⊙M的半径r、CH的长；（3分）‎ ‎（2）如图11，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；（3分）‎ ‎（3）如图12，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．（3分）‎ ‎ ‎ x D A B H C E M O F 图10‎ x y D A B H C E M O F 图11‎ P Q x y D A B H C E M O F 图12‎ N T K y ‎21.（2010广东珠海）21.如图，△ABC内接于⊙O，AB＝6,AC＝4,D是AB边上一点，P是优弧BAC的中点，连结PA、PB、PC、PD.‎ ‎(1)当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并证明；‎ ‎（2）若cos∠PCB=，求PA的长.‎ ‎22.（2010广东珠海）如图，平面直角坐标系中有一矩形ABCD（O为原点），点A、C分别在x轴、y轴上，且C点坐标为（0,6）；将BCD沿BD折叠（D点在OC边上），使C点落在OA边的E点上，并将BAE沿BE折叠，恰好使点A落在BD的点F上.‎ ‎(1)直接写出∠ABE、∠CBD的度数，并求折痕BD所在直线的函数解析式；‎ ‎(2)过F点作FG⊥x轴，垂足为G，FG的中点为H，若抛物线经过B、H、D三点，求抛物线的函数解析式；‎ ‎(3)若点P是矩形内部的点，且点P在（2）中的抛物线上运动（不含B、D点），过点P作PN⊥BC分别交BC和BD于点N、M，设h=PM-MN，试求出h与P点横坐标x的函数解析式，并画出该函数的简图，分别写出使PMMN成立的x的取值范围。‎ ‎ ‎ ‎23.（2010广东梅州）如图9，中，点P是边上的一个动点，过P作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．‎ ‎（1）求证:PE=PF；‎ ‎（2）当点P在边上运动时，四边形BCFE可能是菱形吗？说明理由；‎ ‎（3）若在AC边上存在点P,使四边形AECF是正方形,且.求此时∠A的大小.‎ ‎24.（2010广东梅州）图10‎ 直角梯形OABC中，OC∥AB，C（0，3），B（4，1），以BC为直径的圆交轴于E，D两点（D点在E点右方）.‎ ‎（1）求点E,D 的坐标;‎ ‎（2）求过B,C,D三点的抛物线的函数关系式；‎ ‎(3)过B,C,D三点的抛物线上是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标. ‎ 答 案 ‎1.（2010广东中山）（1）提示： （2）30（度）‎ ‎2.（2010广东中山）（1）原式 （2） ‎ ‎（3）1260‎ ‎3.（2010广东中山）提示：∵PQ∥FN，PW∥MN ∴∠QPW =∠PWF，∠PWF =∠MNF ∴∠QPW =∠MNF ‎ 同理可得：∠PQW =∠NFM或∠PWQ =∠NFM ∴△FMN∽△QWP ‎ ‎（2）当时，△PQW为直角三角形；‎ 当0≤x<，CF,‎ ‎∴PE+PF>CF 即EF>CF┄┄5′‎ 又菱形的四条边都相等，‎ 所以四边形BCFE不可能是菱形。┄┄6′‎ ‎⑶若四边形AECF 是正方形。则AP=CP, ∠ACE=‎ ‎∵∠BCE=∠PCE ‎∴∠BCA=┄┄7′‎ 又∵‎ ‎∴即tan∠B＝┄┄8′‎ ‎∴∠B＝60°∴∠A=90°-∠B=30°┄┄9′‎ ‎7.（2010广东河源）解：⑴,在BC上取中点G,并过G作GH⊥x轴于H ,连接GD,‎ ‎ ∵,‎ ‎∴G∴H(2,0) ┄┄1′‎ ‎∵BC=,GH=2-0=2‎ 又DG=BG=‎ ‎∴HD=‎ ‎∴D(3,0),E(1,0) ┄┄2′‎ ‎⑵设过B、C、D三点的抛物线表达式为则，‎ ‎ ┄┄3′‎ 解得， ┄┄4′‎ ‎∴┄┄5′‎ ‎⑶设Q，由（2）可得Q。过Q作QN⊥X轴于N 分2种情况：‎ ‎①当∠BDQ=90时，∴∠NDQ+∠BDA=90° ‎ ‎∵∠DNQ=∠BAD=90 ∴∠NDQ+∠NQD=90°∴∠NQD=∠BDA ‎∴△NDQ∽△ABD ∴┄┄6′‎ 即 解得，‎ 当，当，‎ ‎∴,(与点D重合，舍去) ┄┄7′‎ ‎② 当∠DBQ=90时，则有 ,‎ ‎∵B(4,1),D(3,0),Q， ‎ ‎∴BD=‎ ‎∴+2＝‎ 整理得，，解得，┄┄8′‎ ‎∴当时，＝1,（此时，Q点与B点重合，舍去）当时，‎ ‎∴(与点B重合，舍去)，‎ 综上所述符合条件的点有2个，分别是，.┄┄9′‎ ‎8.（肇庆市2010）解：(1)图象的另一支在第三象限． (2分)‎ 由图象可知，>0，解得：>2 (4分)‎ ‎(2)将点(3，1)代入得：，‎ 解得： (6分)‎ ‎(3)∵>0，∴在这个函数图象的任一支上，随减少而增大， ‎ ‎ ∴当1<2 时 ，1>2 (8分)‎ ‎9.（肇庆市2010）(本小题满分10分)‎ ‎(1)∵∠B、∠F同对劣弧AP ，∴ ∠B ＝∠F (1分)‎ ‎∵BO＝PO，∴∠B ＝∠B PO (2分)‎ ‎∴∠F＝∠B P F，∴AF∥BE (3分)‎ ‎(2)∵AC切⊙O于点A，AB是⊙O的直径，‎ ‎ ∴ ∠BAC＝90°‎ ‎∵ AB是⊙O的直径， ∴ ∠B PA＝90° (4分)‎ ‎∴∠EA P ＝90°—∠BE A，∠B＝90°—∠BE A，‎ ‎∴∠EA P ＝∠B＝∠F (5分)‎ 又∠C＝∠C，∴△ACP∽△FCA (6分)‎ ‎ (3)∵ ∠C PE＝ ∠B PO＝∠B＝∠EA P， ∠C＝∠C ‎ ‎ ∴△P C E ∽△ACP ∴ (7分)‎ ‎∵∠EA P＝∠B，∠E P A ＝∠A P B ＝90°‎ ‎∴△EA P ∽△A B P ∴ (8分)‎ 又AC＝AB，∴ (9分)‎ 于是有 ∴CP＝AE． (10分)‎ ‎10.（肇庆市2010）(1)证明：将点P(2，1)代入得： ‎ 整理得： (2分)‎ ‎(2)解：∵ ∴＝ (4分)‎ ‎∵—2<0 ∴当＝ —1时，有最大值2； (5分)‎ ‎(3)解：由题意得：，‎ ‎∴＝︱—︱＝，即︱—︱ ＝ (6分)‎ 亦即 (7分)‎ 由根与系数关系得：， (8分)‎ 代入得：，‎ 整理得： (9分)‎ 解得：，经检验均合题意． (10分)‎ ‎11.（2010.广东茂名）‎ ‎12.（2010.广东茂名）‎ 12. ‎13.(2010广东湛江）解：（1）当0≤≤2时,设函数解析式为，由题意得 1分 ‎ 解得 3分 当0≤≤2时,函数解析式为. 4分 ‎（2）当＞2时，设函数解析式为，由题意得 5分 ‎ 解得 7分 当＞2时，函数解析式为. 8分 ‎（3）把代入中，得 ，解得 9分 ‎ 把代入中，得 ，解得 10分 ‎（小时） 11分 答：服药一次,治疗疾病的有效时间是3小时． 12分 ‎14.(2010广东湛江）解：（1） A（5，0）, 1分 由抛物线经过原点O，可设抛物线的解析式为，得 2分 ‎ 解得 4分 抛物线的解析式为 5分 ‎（2）如图，由（1）得抛物线的对称轴是直线，点O、A关于直线对称.‎ 连接AB交直线于点C，则点C使BC+OC的值最小.……………………………6分 设直线AB的解析式为y=kx+b，得 解得 ‎ 直线AB的解析式为 ………………………8分 把x=代入，得 点C的坐标为（，）. …………………………9分 ‎（3）如图，过P作y轴的平行线交AB于点D，设点P的横坐标为x,得 P ， D……………10分 ‎ ‎ ‎ ‎ ‎ ‎ 当时，有最大值为. 12分 把代入，得 此时点P的坐标为,△PAB的最大面积为. 13分 ‎15.（2010广东佛山）（1）是第二类知识。………………………………………………1分 ‎ （2）单项式乘以多项式（分配律），字母表示数，数可以表示线段的长或图形的面积，等等。…………………………………………4分 ‎（3）用数来说明：（a+b）（c+d）=（a+b）c+（a+b）d=ac+bc+ad+bd。………(2分+1分)……………………………………………………………7分 ‎ 用形来说明：如右图，边长为a+b和c+d的矩形，……………9分 分割前后的面积相等，‎ 即（a+b）（c+d）=ac+bc+ad+bd。……………………………………10分（1）‎ ‎16.（2010广东佛山）（i）如图，若点D在线段AB上，‎ 由于∠ACB＞∠ABC，可以作一个点D满足∠ACD=∠ABC, ‎ 使得△ACD∽△ABC。………………………………………1分 ‎(ii)如图①，若点D在线段AB的延长线上，‎ 则∠ACD＞∠ACB＞∠ABC，与条件矛盾，‎ 因此，这样的点D不存在。…………………………2分 ‎（iii）如图②，若点D在线段AB的反向延长线上，‎ 由于∠BAC是锐角，则∠BAC＜90°＜∠CAD，‎ 不可能有△ACD∽△ABC.‎ 因此，这样的点D不存在。……………………………………6分 综上所述，这样的点D有一个。………………………………7分 注：（iii）中用“∠CAD是钝角，△ABC中只可能∠ACB是钝角，而∠CAD＞∠ACB”说明不存在点D亦可。‎ ‎（2）若∠BAC为锐角，由（1）知，这样的点D有一个；‎ ‎ 若∠BAC为直角，这样的点D有两个；………………………9分 ‎ 若∠BAC为钝角，这样的点D有一个。………………………11分 ‎17.（2010广州）解：（1）连接OA，取OP与AB的交点为F，则有OA＝1．‎C P D O B A E C P D O B A E F C P D O B A E H G ‎∵弦AB垂直平分线段OP，∴OF＝OP＝，AF＝BF．‎ 在Rt△OAF中，∵AF＝＝＝，∴AB＝2AF＝．‎ ‎（2）∠ACB是定值.‎ 理由：由（1）易知，∠AOB＝120°，‎ 因为点D为△ABC的内心，所以，连结AD、BD，则∠CAB＝2∠DAE，∠CBA＝2∠DBA，‎ 因为∠DAE＋∠DBA＝∠AOB＝60°，所以∠CAB＋∠CBA＝120°，所以∠ACB＝60°；‎ ‎（3）记△ABC的周长为l，取AC，BC与⊙D的切点分别为G，H，连接DG，DC，DH，则有DG＝DH＝DE，DG⊥AC，DH⊥BC.‎ ‎∴‎ ‎＝AB•DE＋BC•DH＋AC•DG＝(AB＋BC＋AC) •DE＝l•DE．‎ ‎∵＝4，∴＝4，∴l＝8DE.‎ ‎∵CG，CH是⊙D的切线，∴∠GCD＝∠ACB＝30°，‎ ‎∴在Rt△CGD中，CG＝＝＝DE，∴CH＝CG＝DE．‎ 又由切线长定理可知AG＝AE，BH＝BE，‎ ‎∴l＝AB＋BC＋AC＝2＋2DE＝8DE，解得DE＝3，‎ ‎∴△ABC的周长为24．‎ ‎18.（2010广州）【答案】（1）由题意得B（3，1）．‎ 若直线经过点A（3，0）时，则b＝‎ 若直线经过点B（3，1）时，则b＝‎ 若直线经过点C（0，1）时，则b＝1‎ ‎①若直线与折线OAB的交点在OA上时，即1＜b≤，如图25-a，‎ ‎ 此时E（2b，0）‎ ‎∴S＝OE·CO＝×2b×1＝b 图3‎ ‎②若直线与折线OAB的交点在BA上时，即＜b＜，如图2‎图1‎ 图2‎ 此时E（3，），D（2b－2，1）‎ ‎∴S＝S矩－(S△OCD＋S△OAE ＋S△DBE )‎ ‎＝ 3－[(2b－1)×1＋×(5－2b)·()＋×3()]＝‎ ‎∴‎ ‎（2）如图3，设O1A1与CB相交于点M，OA与C1B1相交于点N，则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。‎ 由题意知，DM∥NE，DN∥ME，∴四边形DNEM为平行四边形 根据轴对称知，∠MED＝∠NED 又∠MDE＝∠NED，∴∠MED＝∠MDE，∴MD＝ME，∴平行四边形DNEM为菱形．‎ 过点D作DH⊥OA，垂足为H，‎ 由题易知，tan∠DEN＝，DH＝1，∴HE＝2，‎ 设菱形DNEM 的边长为a，‎ 则在Rt△DHM中，由勾股定理知：，∴‎ ‎∴S四边形DNEM＝NE·DH＝‎ ‎∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化，面积始终为．‎ ‎19.（2010广东深圳）（1）、因为点A、B均在抛物线上，故点A、B的坐标适合抛物线方程 ‎∴ 解之得：；故为所求 ‎（2）如图2，连接BD，交y轴于点M，则点M就是所求作的点 设BD的解析式为，则有，，‎ 故BD的解析式为；令则，故 ‎(3)、如图3，连接AM，BC交y轴于点N，由（2）知，OM=OA=OD=2，‎ 图3‎ 易知BN=MN=1， 易求 ‎；设，‎ 依题意有：，即：‎ 解之得：，，故 符合条件的P点有三个：‎ ‎20.（2010广东深圳）（1）、如图4，OE=5，，CH=2‎ F 图4‎ ‎（2）、如图5，连接QC、QD，则，‎ 易知，故，‎ ‎，，由于，‎ ‎；‎ ‎（3）、如图6，连接AK，AM，延长AM，‎ 与圆交于点G，连接TG，则 ‎，‎ 由于，故，；‎ 而，故 在和中，；‎ 故；‎ 图5‎ F ‎;‎ 即：‎ 故存在常数，始终满足 常数 F 图6‎ ‎1‎ ‎21.（2010广东珠海）.解：（1）当BD＝AC＝4时，△PAD是以AD为底边的等腰三角形 ‎∵P是优弧BAC的中点 ∴弧PB＝弧PC ‎∴PB＝PC ‎∵BD＝AC＝4 ∠PBD=∠PCA ‎∴△PBD≌△PCA ‎∴PA=PD 即△PAD是以AD为底边的等腰三角形 ‎（2）由（1）可知，当BD＝4时，PD＝PA，AD＝AB-BD＝6-4＝2‎ 过点P作PE⊥AD于E，则AE＝AD=1‎ ‎∵∠PCB=∠PAD∴cos∠PAD=cos∠PCB=∴PA=‎ ‎22.（2010广东珠海）解：（1）∠ABE＝∠CBD=30° ‎ 在△ABE中，AB＝6‎ BC=BE=‎ CD=BCtan30°=4‎ ‎∴OD=OC-CD=2‎ ‎∴B(，6) D(0,2)‎ 设BD所在直线的函数解析式是y=kx+b ‎ ∴ ‎ 所以BD所在直线的函数解析式是 ‎(2)∵EF=EA=ABtan30°= ∠FEG=180°-∠FEB-∠AEB=60°‎ 又∵FG⊥OA ‎ ‎∴FG＝EFsin60°=3 GE=EFcos60°= OG=OA-AE-GE=‎ 又H为FG中点 ‎∴H（，） …………4分 ‎∵B(，6) 、 D(0,2)、 H（，）在抛物线图象上 ‎ ‎ ∴ ‎ ‎∴抛物线的解析式是 ‎(2)∵MP=‎ MN=6-‎ H=MP-MN=‎ 由得 该函数简图如图所示：‎ 当00，即HP>MN ‎23.（2010广东梅州）（1）证明: ∵EC平分∠BCA, ∴∠BCE=∠PCE.‎ ‎∵，∴∠PEC=∠BCE.‎ ‎∴∠PEC=∠PCE, ∴PE=PC. …………2分 同理可证PC=PF.‎ ‎∴PE=PF. …………………………………3分 ‎（2）四边形不可能是菱形. …………………4分 若为菱形，则，而由（1）可知.…………………………………5分 因为在平面内过同一点不可能有两条直线同垂直于一条直线,所以不能成立,所以四边形不可能是菱形. …………………6分 ‎（3）当为正方形时，P是AC的中点,且．‎ ‎∵，∴.‎ ‎∴是以为直角的直角三角形.………………………………… …8分 ‎∵,在Rt△ABC中, .‎ ‎∴∠A=30°. ‎ ‎24.（2010广东梅州）解：（1）∵B(4,1),则A(4,0),设OD=,得DA=4-. ‎ 因为D是以BC为直径的圆与轴的交点, ‎ ‎∴∠CDB=90°,∴∠ODC+ ∠BDA=90°.‎ ‎∵∠OCD+∠ODC=90°, ∴∠OCD= ∠BDA..‎ ‎∴Rt△OCD∽Rt△ADB.‎ ‎ ∴.……………………………3分 ‎,即 解得 可得E(1,0),D(3,0). …………………………4分 ‎(2) ∵C(0,3),D(3,0),B(4,1).‎ 设过此三点的抛物线为则.……………6分 解得.‎ 过B,C,D三点的抛物线的函数关系式为. …………7分 ‎（3）假设存在，分两种情况讨论：‎ ‎①当∠BDQ=90°时，由(1)可知∠BDC=90°，且点在抛物线上，故点与点重合，所求的点为（0，3）; …………………………………8分 ‎②当∠DBQ=90°时，过点B作平行于DC的直线BQ，假设直线BQ交抛物线于另一点Q.‎ ‎∵D（3，0），C(0,3)，直线DC为. ………………………8.5分 ‎∵BQ∥DC,故可设直线BQ为.‎ 将B(4,1)代入,得m=5.(或直线DC向上平移2个单位与直线BQ重合)‎ 直线BQ为. …………………………………9分 由.得.或.‎ 又点B(4,1), ∴Q(-1,6).‎ 故该抛物线上存在两点(0,3),(-1,6)满足条件．…………………………………11分