2006年天津市中考数学试卷及答案

2006年天津市中考数学试卷及答案

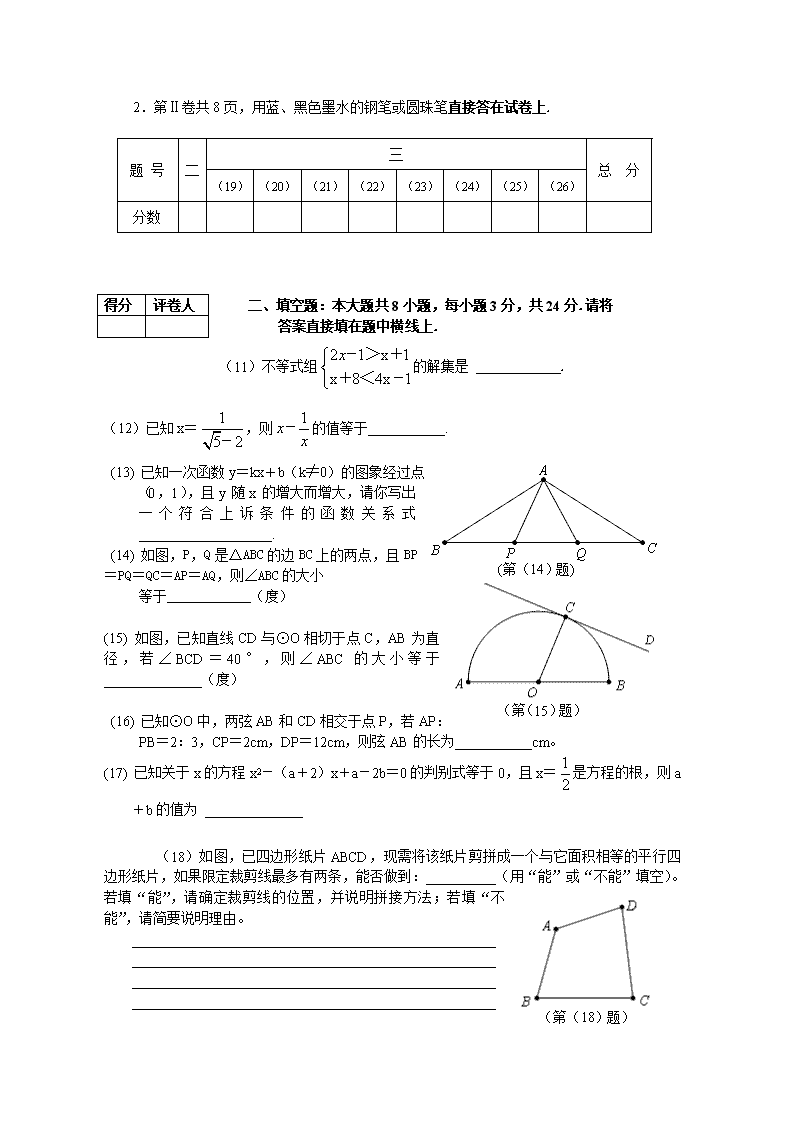
‎2006年天津市初中毕业生学业考试数学试卷 本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第Ⅰ卷第1页至第二页， 第Ⅱ卷第3页至第10页试卷满分120分，考试时间100分钟.‎ 第Ⅰ卷（选择题 共30分）‎ 一、 选择题：本大题共10小题，每小题3分，共30分.在每小题给出的4个选项中，只有1项是符合题目要求的.‎ (1) ‎ tan30°的值等于 ‎(A) （B) (C) (D) ‎ ‎(2) 下列判断中正确的是 ‎（A）四边相等的四边形是正方形 ‎ (B) 四角相等的四边形是正方形 ‎(C) 对角线互相垂直的平行四边形是正方形 ‎(D) 对角线互相垂直平分且相等的四边形是正方形 ‎(3) 下列图形中，为轴对称图形的是 ‎ ‎ ‎(4) 已知，则的值等于 ‎（A）6 （B）－6 （C） （D） ‎ ‎(5) 若0＜x＜1，则x，x2，x3的大小关系是 ‎（A）x＜x2＜x3 （B）x＜x3＜x2 （C）x3＜x2＜x （D）x2＜x3＜x ‎(6) 如图，在梯形ABCD中，AB//CD，中位线EF与 对角线AC、BD交于M、N两点，若EF＝‎18cm，‎ 数学试卷 第1页（共10页） 数学试卷 第2页（共10页）‎ MN＝‎8cm，则AB的长等于 ‎（A‎10cm （B）‎13cm（C）‎20cm （D）‎26cm ‎ ‎ (7) 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3，r4，r6，则r3：r4：r6等于 ‎（A） (B)‎ ‎ (C) (D) ‎ ‎ (8) 如图，AB//CD，AE//FD，AE、FD分别交BC于点G、H，则图中共有相似三角形 ‎（A）4对 (B) 5对 ‎ ‎(C) 6对 (D)7对 ‎(9) 如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：‎ ‎① △ACE≌△DCB； ② CM＝CN；③ AC＝DN。其中，正确结论的个数是 ‎(A) 3个 （B）2个 ‎ (C) 1个 （D）0个 ‎ ‎(10) 已知实数a，b，c满足a2＋b2＝1，b2＋c2＝2，c2＋a2＝2，则ab＋bc＋ca的最小值为 ‎（A） (B) ‎ ‎(C) (D) ‎ ‎ ‎ ‎2006年天津市初中毕业生学业考试数学试卷 座 位 号 ‎（准考证号末两位）‎ ‎ ‎ 第Ⅱ卷 (非选择题 共90分)‎ 注意事项:‎ ‎1．答第Ⅱ卷时，考生务必将密封线内的项目和试卷第三页右上角的“座位号”填写清楚. ‎ ‎2．第Ⅱ卷共8页，用蓝、黑色墨水的钢笔或圆珠笔直接答在试卷上.‎ 题 号 二 三 总 分 ‎（19）‎ ‎（20）‎ ‎（21）‎ ‎（22）‎ ‎（23）‎ ‎（24）‎ ‎（25）‎ ‎（26）‎ 分数 得分 评卷人 二、填空题：本大题共8小题，每小题3分，共24分.请将 答案直接填在题中横线上.‎ ‎（11）不等式组的解集是 .‎ ‎(第（14）题)‎ ‎（12）已知x＝，则的值等于___________.‎ ‎(13) 已知一次函数y＝kx＋b（k≠0）的图象经过点（0，1），且y随x的增大而增大，请你写出一个符合上诉条件的函数关系式___________________.‎ ‎（第（15）题）‎ ‎(14) 如图，P，Q是△ABC的边BC上的两点，且BP＝PQ＝QC＝AP＝AQ，则∠ABC的大小 等于____________（度）‎ ‎(15) 如图，已知直线CD与⊙O相切于点C，AB为直径，若∠BCD＝40°，则∠ABC的大小等于______________（度）‎ ‎(16) 已知⊙O中，两弦AB和CD相交于点P，若AP：PB＝2：3，CP＝‎2cm，DP＝‎12cm，则弦AB的长为___________cm。‎ ‎(17) 已知关于x的方程x2－（a＋2）x＋a－2b＝0的判别式等于0，且x＝是方程的根，则a＋b的值为 ______________‎ ‎（第（18）题）‎ ‎（18）如图，已四边形纸片ABCD，现需将该纸片剪拼成一个与它面积相等的平行四边形纸片，如果限定裁剪线最多有两条，能否做到：__________（用“能”或“不能”填空）。若填“能”，请确定裁剪线的位置，并说明拼接方法；若填“不能”，请简要说明理由。‎ ‎____________________________________________________‎ ‎____________________________________________________‎ ‎____________________________________________________‎ ‎____________________________________________________‎ ‎____________________________________________________‎ 三、解答题：本大题共8小题，共66分。解答应写出文字说明、演算步骤或证明过程.‎ 得分 评卷人 ‎（19）（本小题6分）‎ 为了调查七年级某班学生每天完成家庭作业所需的时间，在该班随机抽查了 8名学生，他们每天完成作业所需时间（单位：分）分别为：60，55，75，55，55，43，65，40。‎ ‎（Ⅰ）求这组数据的众数、中位数；‎ ‎（Ⅱ）求这8名学生每天完成家庭作业的平均时间；如果按照学校要求，学生每天完成家庭作业时间不能超过60分钟，问该班学生每天完成家庭作业的平均时间是否符合学校的要求？‎ 得分 评卷人 得分 评卷人 ‎（20）（本小题8分）‎ ‎ 已知正比例函数y＝kx（k≠0）和反比例函数y＝的图象都经过点（4，2）。‎ ‎（Ⅰ）求这两个函数的解析式；‎ ‎（Ⅱ）这两个函数图象还有其他交点吗？若有，请求出交点的坐标；若没有，请说明理由。‎ 得分 评卷人 ‎（21）（本小题8分）‎ 已知抛物线y＝4x2－11x－3.‎ ‎（Ⅰ）求它的对称轴；‎ ‎（Ⅱ）求它与x轴、y轴的交点坐标.‎ ‎（22）（.本小题8分）‎ ‎ ‎ 如图，已知⊙O的割线PAB交⊙O于A、B两点，PO与⊙O交于点C，且PA＝AB＝‎6cm，PO＝‎‎12cm ‎（Ⅰ）求⊙O的半径；‎ ‎（Ⅱ）求△PBO的面积.‎ ‎（结果可带根号） ‎ 得分 评卷人 ‎（23）（本小题8分）‎ ‎ 如图，在观测点E测得小山上铁塔顶A的仰角为60°，铁塔底部B的仰角为45°。已知塔高AB＝‎20m，观察点E到地面的距离EF＝‎35cm，求小山BD的高（精确到0.1海里，≈1.732）。‎ ‎ ‎ ‎ ‎ ‎ （24）（本小题8分） ‎ ‎ ‎ ‎ 注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答；也可以选用其他的解题方案，此时不必填空，，只需按照解答题的一般要求，进行解答。‎ 某农场开挖一条长‎960米的渠道，开工后每天比原计划多挖‎20米，结果提前4天完成任务，原计划每天挖多少米？‎ 解题方案 设原计划每天挖x米，‎ ‎（Ⅰ）用含x的代数式表示：‎ 开工后实际每天挖______________米，‎ 完成任务原计划用______________天，实际用_______________天；‎ ‎（Ⅱ）根据题意，列出相应方程_________________________________;‎ ‎（Ⅲ）解这个方程，得_______________；‎ ‎（Ⅳ）检验：_________________________________;‎ ‎（Ⅴ）答：原计划每天挖_________________米（用数字作答）。‎ 得分 评卷人 ‎（25）（本小题10分） ‎ ‎ ‎ 已知Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8。‎ ‎（Ⅰ）如图①，若半径为r1的⊙O1是Rt△ABC的内切圆，求r1；‎ 图①‎ ‎（Ⅱ）如图②，若半径为r2的两个等圆⊙O1、⊙O2外切，且⊙O1与AC、AB相切，⊙O2与BC、AB相切，求r2；‎ 图②‎ www.1230.org ‎（Ⅲ）如图③，当n大于2的正整数时，若半径rn的n个等圆⊙O1、⊙O2、…、⊙On 依次外切，且⊙O1与AC、BC相切，⊙On与BC、AB相切，⊙O1、⊙O2、⊙O3、…、⊙On－1均与AB边相切，求rn.‎ 图③‎ ‎ ‎ ‎ (26) (本小题10分)‎ 已知抛物线y＝ax2＋bx＋c的定点坐标为(2,4). ‎ ‎（Ⅰ）试用含a的代数式分别表示b，c；‎ ‎（Ⅱ）若直线y＝kx＋4（k≠0）与y轴及该抛物线的交点依次为D、E、F，且，其中O为坐标原点，试用含a的代数式表示k；‎ ‎（Ⅲ）在（Ⅱ）的条件下，若线段EF的长m满足，试确定a的取值范围。‎ 参考答案及评分标准 一、选择题：本大题共10小题，每小题3分，共30分。‎ ‎1．C ‎ ‎2．D ‎ ‎3．B ‎ ‎4．A ‎ ‎5．C ‎6．D ‎ ‎7．A ‎ ‎8．C ‎ ‎9．B ‎ ‎10．D 二、填空题：本大题共8小题，每小题3人，共24分。‎ ‎11．x>3 ‎ ‎12．4‎ ‎13．如：1 ‎ ‎14．120°‎ ‎15．50° ‎ ‎16．10‎ ‎17．‎ ‎18．能 如图，取四边形ABCD各边的中点E、G、F、H，连接EF、GH，则EF、GH为裁剪线。EF、GH将四边形ABCD分成1、2、3、4四个部分，拼接时，图中的1不动，将2、4分别绕点H、F各旋转180°，3平称，拼成的四边形满足条件。‎ 三、解答题：本大题共8小题。共66分。‎ ‎19．本小题满分6分。‎ 解：（I）在这8个数据中，55出现了3次，出现的次数最多，即这组数据的众数是55；‎ 将这8个数据按从小到大的顺序排列，其中最中间的两个数据都是55，‎ 即这组数据的中位数是55。 3分 ‎（II）∵这8个数据的平均数是 ‎（分）‎ ‎∴这8名学生完成家庭作业所需的平均时间为56分钟。 5分 因为56<60‎ 由此估计该班学生每天完成家庭作业的平均时间符合学校的要求。 6分 ‎20．本小题满分8分。‎ 解：（I）∵点A（4，2）在正比例函数y=kx的图象上，‎ 有，即 ‎∴正比例函数的解析式为 3分 又∵点A（4，2）在反比例函数的图象上 有，即 ‎∴反比例函数的解析式为 6分 ‎（II）这两个函数的图象还有一个交点。 7分 由解得或 ‎∴这两个函数图象的另一个交点坐标为（－4，－2） 8分 ‎21．本小题满分8分。‎ 解：（I）由已知，a=4，b=－11，得 ‎∴该抛物线的对称轴是 2分 ‎（II）令y=0，得，解得 ‎∴该抛物线与x轴的交点坐标为（3，0），（，0） 6分 令x=0，得y=－3‎ ‎∴该抛物线与y轴的交点坐标为（0，－3）。 8分 ‎22．本小题满分8分。‎ 解：（I）设圆O的半径为r，PO的延长线交圆O于点D。‎ 根据切割线定理的推论，有 PA·PB=PC·PD ‎∵PB=PA+AB=12‎ PC=PO－CO=12－r PD=PO+OD=12+r ‎∴（12－r）（12+r）=6×12‎ 取正数解，得 ‎∴圆O的半径为 3分 ‎（II）过点O作OE⊥AB，垂足为E，则 在Rt△EBO中，由勾股定理，得 ‎ 6分 ‎∴△PBO的面积为 ‎ 8分 ‎23．本小题满分8分。‎ 解：如图，过点E作EG⊥AD于点G 由已知，得 ‎∠AEG=60°，∠BEG=45° 2分 在Rt△BEG中，BG=EG 在Rt△AEG中，由，得 又AG=AB+BG=20+BG ‎，即 6分 ‎∵BD=BG+GD，GD=EF=35‎ 答：小山BD的高约为‎62.3m 8分 ‎24．本小题满分8分。‎ 解：（I） 3分 ‎（II） 4分 ‎（III） 6分 ‎（IV）都是原方程的根，但负数不合题意，所以只取x=60 7分 ‎（V）60 8分 ‎25．本小题满分10分。‎ 解：（I）∵在Rt△ABC中，∠ACB=90°，AC=6，BC=8‎ ‎ 1分 如图，设圆O1与Rt△ABC的边AB、BC、CA分别切于点D、E、F 连接 于是，‎ ‎ 2分 又 3分 ‎ 4分 ‎（II）如图，连接，则 ‎∵等圆圆O1、圆O2外切 ‎，且 过点C作CM⊥AB于点M，交于点N，则 ‎ 5分 ‎ 6分 ‎ 7分 解得 8分 ‎（III）如图，连接，则 ‎∵等圆圆O1、圆O2、…、圆On依次外切，且均与AB边相切。‎ ‎∴均在直线上，且 ‎ 9分 过点C作CH⊥AB于点H，交于点K 则 解得 10分 ‎26．本小题满分10分。‎ 解：（I）由已知，可设抛物线的顶点式为 即 ‎ 2分 ‎（II）设E（）、F（）‎ 由方程组 消去y，得 （*）‎ ‎ ①‎ ‎ ②‎ 又 ‎。。即 由②，知x1与x2同号，∴x2=4x1 ③ 5分 由②、③，得x1=1，x2=4；x1=－1，x2=－4‎ 将上面数值代入①，得 解得k=a或k=－‎‎9a 经验证，方程（*）的判别式△>0成立。‎ ‎∴k=a或k=－‎9a 7分 ‎（III）由勾股定理，得 而 由，得 ‎，即 8分 由已知 ‎，即 或 当k=a时，有1≤a≤2或－2≤a≤－1‎ 当k=－‎9a时，有1≤－9≤2或－2≤－‎9a≤－1‎ 即或 10分