2020中考数学一轮复习 习题分类汇编十一（三角形1）（无答案） 鲁教版

2020中考数学一轮复习 习题分类汇编十一（三角形1）（无答案） 鲁教版

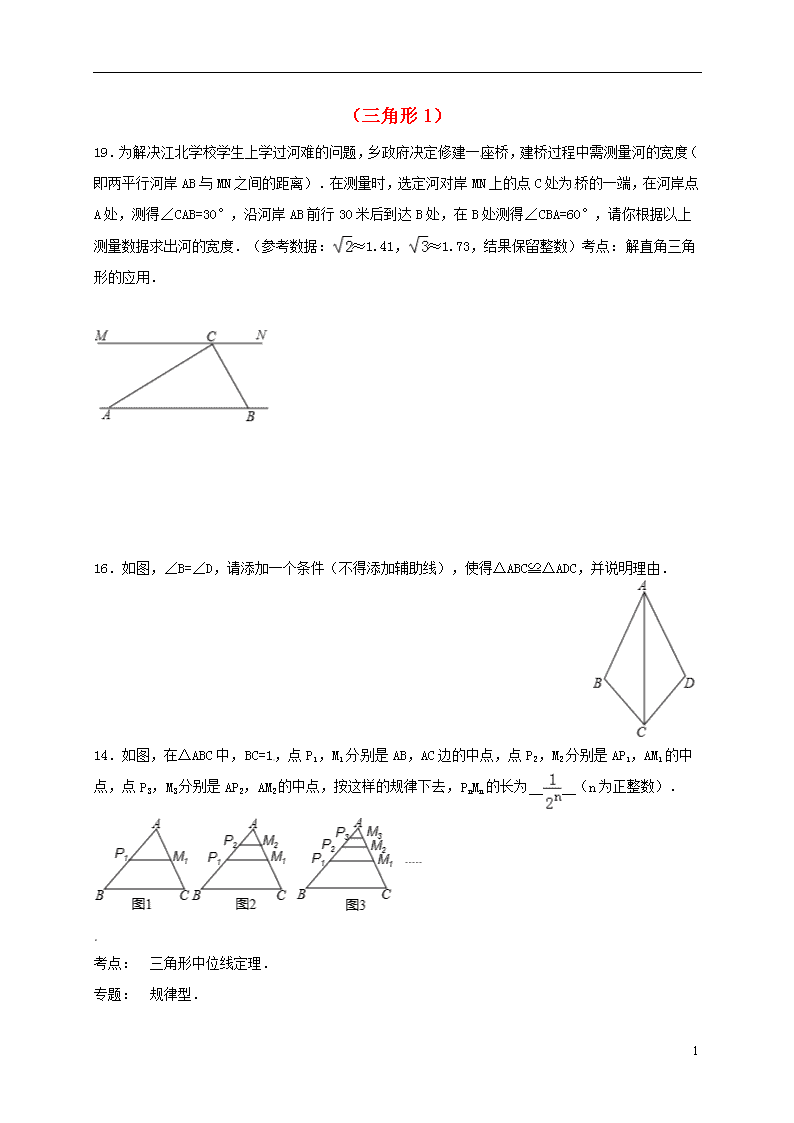
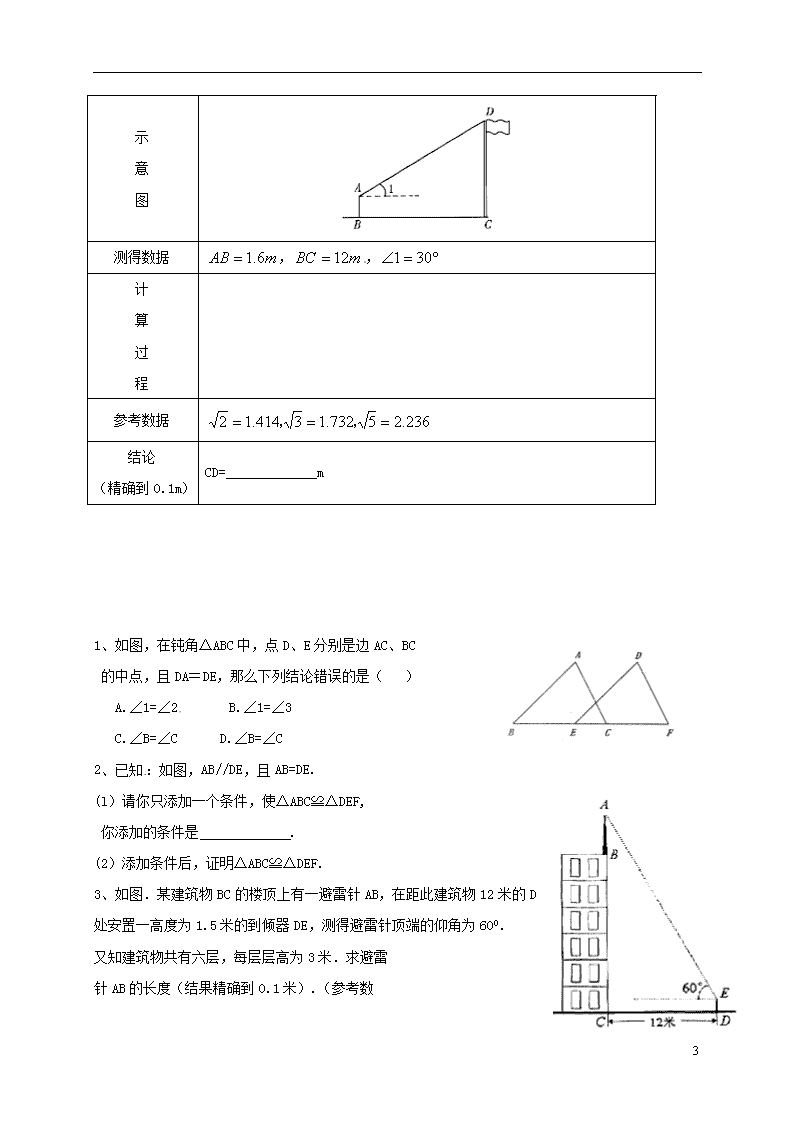
‎（三角形1）‎ ‎19．为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行‎30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据：≈1.41，≈1.73，结果保留整数）考点： 解直角三角形的应用．‎ ‎16．如图，∠B=∠D，请添加一个条件（不得添加辅助线），使得△ABC≌△ADC，并说明理由．‎ ‎14．如图，在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，按这样的规律下去，PnMn的长为　　（n为正整数）．‎ 考点： 三角形中位线定理．‎ 专题： 规律型．‎ 4‎ ‎1、小颖在做下面的数学作业时，因钢笔漏墨水，不小心将部分迹污损了。作业过程如下（涂黑部分即污损部分）：‎ 已知：如图，OP平分∠AOB，MN//OB 求证：OM=NM 证明：因为OP平分∠AOB 所以 ‎ 又因为MN//OB 所以 ‎ 故∠1=∠3‎ 所以OM=NM 小颖思考：污损部分应分别是以下四项中的二项：‎ ‎①∠1=∠2 ②∠2=∠3 ③∠3=∠4 ④∠1=∠4‎ 那么她补出来的结果应是（ ）‎ A. ①④ B. ②③ C. ①② D. ③④‎ ‎2、九年级（3）班在完成测量校内旗杆高度的数学活动后，小明填写了如下《数学活动报告》中的附件（运算表）的一部分。请你根据此图表提供的示意图及相关数据，完成此表未完成的部分：‎ 课题 测量校内旗杆高度 4‎ 示 意 图 测得数据 ‎，，‎ 计 算 过 程 参考数据 结论 ‎（精确到‎0.1m）‎ CD=_____________m ‎1、如图，在钝角△ABC中，点D、E分别是边AC、BC ‎ 的中点，且DA＝DE，那么下列结论错误的是（ ）‎ ‎ A.∠1=∠2 B.∠1=∠3 ‎ ‎ C.∠B=∠C D.∠B=∠C ‎2、已知：如图，AB//DE，且AB=DE. ‎ ‎(l）请你只添加一个条件，使△ABC≌△DEF,‎ ‎ 你添加的条件是 .‎ ‎(2）添加条件后，证明△ABC≌△DEF.‎ ‎3、如图．某建筑物BC的楼顶上有一避雷针AB，在距此建筑物‎12米的D处安置一高度为‎1.5米的到倾器DE，测得避雷针顶端的仰角为600．‎ 又知建筑物共有六层，每层层高为‎3米．求避雷 针AB的长度（结果精确到‎0.1米）.（参考数 4‎ 据：）‎ ‎1、如图，在中，平分且与BC相交于点，∠B = 40°，∠BAD = 30°，则的度数是（ ）‎ A．70° B．80° C．100° D．110°‎ 第1题 ‎ ‎2、已知：如图，在ABC中，∠B = 45°，∠C = 60°，AB = 6．求BC的长（结果保留根号）．‎ 4‎