- 2021-05-13 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学复习专题几何综合题含答案解析
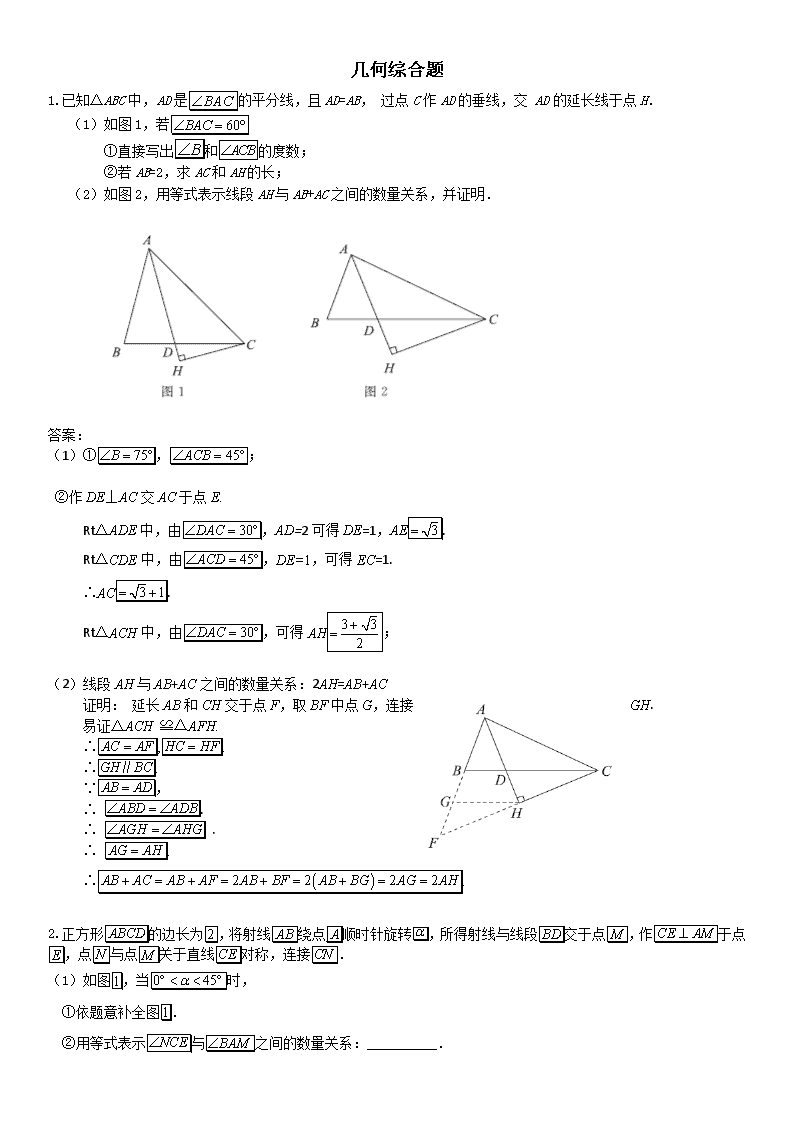
几何综合题 1.已知△ABC中,AD是的平分线,且AD=AB, 过点C作AD的垂线,交 AD的延长线于点H. (1)如图1,若 ①直接写出和的度数; ②若AB=2,求AC和AH的长; (2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明. 答案: (1)①,; ②作DE⊥AC交AC于点E. Rt△ADE中,由,AD=2可得DE=1,AE. Rt△CDE中,由,DE=1,可得EC=1. ∴AC. Rt△ACH中,由,可得AH; (2)线段AH与AB+AC之间的数量关系:2AH=AB+AC 证明: 延长AB和CH交于点F,取BF中点G,连接GH. 易证△ACH ≌△AFH. ∴,. ∴. ∵, ∴ . ∴ . ∴ . ∴. 2.正方形的边长为,将射线绕点顺时针旋转,所得射线与线段交于点,作于点,点与点关于直线对称,连接. (1)如图,当时, ①依题意补全图. ②用等式表示与之间的数量关系:__________. (2)当时,探究与之间的数量关系并加以证明. (3)当时,若边的中点为,直接写出线段长的最大值. 答案:(1)①补全的图形如图7所示. ② ∠NCE=2∠BAM. (2)当45°<α<90°时,. 证明:如图8,连接CM,设射线AM与CD的交点为H. ∵ 四边形ABCD为正方形, ∴ ∠BAD=∠ADC=∠BCD=90°,直线BD为正方形ABCD的对称轴, 点A与点C关于直线BD对称. ∵ 射线AM与线段BD交于点M, ∴ ∠BAM=∠BCM=α. ∴ ∠1=∠2=. ∵ CE⊥AM, ∴ ∠CEH=90°,∠3+∠5=90°. 又∵∠1+∠4=90°,∠4=∠5, ∴ ∠1=∠3. ∴ ∠3=∠2=. ∵ 点N与点M关于直线CE对称, ∴ ∠NCE=∠MCE=∠2+∠3=. (3) 3. 如图,已知,点为射线上的一个动点,过点作,交于点,点在内,且满足,. (1)当时,求的长; (2)在点的运动过程中,请判断是否存在一个定点,使得的值不变?并证明你的判断. 答案: (1)作⊥交于. ∵⊥,, ∴. ∴. ∴. ∵,, ∴,. ∴. ∴. (2)当点在射线上且满足时,的值不变,始终为1.理由如下: 当点与点不重合时,延长到使得. ∵, ∴. ∴. ∵,是公共边, ∴≌. ∴. 作⊥于,⊥于. ∵, ∴. ∵⊥,⊥,⊥, ∴四边形为矩形. ∴. ∵, ∴. ∵⊥, ∴. ∴,即. 当点与点重合时,由上过程可知结论成立. 4. 如图,在菱形ABCD中,∠DAB=60°,点E为AB边上一动点(与点A,B不重合),连接CE,将∠ACE的两边所在射线CE,CA以点C为中心,顺时针旋转120°,分别交射线AD于点F,G. (1)依题意补全图形; (2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示); (3)用等式表示线段AE、AF与CG之间的数量关系,并证明. 答案:(1)补全的图形如图所示. (2)解:由题意可知,∠ECF=∠ACG=120°. ∴∠FCG=∠ACE=α. ∵四边形ABCD是菱形,∠DAB=60°, ∴∠DAC=∠BAC= 30°. ∴∠AGC=30°. ∴∠AFC =α+30°. (3)用等式表示线段AE、AF与CG之间的数量关系为. 证明:作CH⊥AG于点H. 由(2)可知∠BAC=∠DAC=∠AGC=30°. ∴CA=CG. ∴HG =AG. ∵∠ACE =∠GCF,∠CAE =∠CGF, ∴△ACE≌△GCF. ∴AE =FG. 在Rt△HCG中, ∴AG =CG.即AF+AE=CG. 5.如图,Rt△ABC中,∠ACB = 90°,CA = CB,过点C在△ABC外作射线CE,且∠BCE = ,点B关于CE的对称点为点D,连接AD,BD,CD,其中AD,BD分别交射线CE于点M,N. (1)依题意补全图形; (2)当= 30°时,直接写出∠CMA的度数; (3)当0°<< 45°时,用等式表示线段AM,CN之间的数量关系,并证明. 答案:(1)如图; (2)45°; (3)结论:AM=CN. 证明:作AG⊥EC的延长线于点G. ∵点B与点D关于CE对称, ∴CE是BD的垂直平分线. ∴CB=CD. ∴∠1=∠2=. ∵CA=CB,∴CA=CD.∴∠3=∠CAD. ∵∠4=90°, ∴∠3=(180°∠ACD)=(180°90°)=45°. ∴∠5=∠2+∠3=+45°-=45°. ∵∠4=90°,CE是BD的垂直平分线, ∴∠1+∠7=90°,∠1+∠6=90°. ∴∠6=∠7. ∵AG⊥EC, ∴∠G=90°=∠8. ∴在△BCN和△CAG中, ∠8=∠G, ∠7=∠6, BC=CA, ∴△BCN≌△CAG. ∴CN=AG. ∵Rt△AMG中,∠G=90°,∠5=45°, ∴AM=AG. ∴AM=CN. 6.在正方形ABCD中,M是BC边上一点,点P在射线AM上,将线段AP绕点A顺时针旋转得到线段AQ,连接BP,DQ. (1)依题意补全图1; (2)①连接,若点P,Q,D恰好在同一条直线上,求证:; ②若点P,Q,C恰好在同一条直线上,则BP与AB的数量关系为: . 答案:(1)补全图形略 (2)①证明: 连接,如图2, ∵线段绕点顺时针旋转90°得到线段, ∴,. ∵四边形是正方形, ∴,. ∴. ∴△≌△. ∴,. ∵在中,, ∴. ∵在中,, 又∵,, ∴. ②. 7.如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF, 过点B作BG⊥CF于点G,连接AG. (1)求证:∠ABG=∠ACF; (2)用等式表示线段CG,AG,BG之间 的等量关系,并证明. 答案:(1)证明 : ∵ ∠CAB=90°. ∵ BG⊥CF于点G, ∴ ∠BGF=∠CAB=90°. ∵∠GFB=∠CFA. ∴ ∠ABG=∠ACF. (2)CG=AG+BG. 证明:在CG上截取CH=BG,连接AH, ∵ △ABC是等腰直角三角形, ∴ ∠CAB=90°,AB=AC. ∵ ∠ABG=∠ACH. ∴ △ABG≌△ACH. ∴ AG =AH,∠GAB=∠HAC. ∴ ∠GAH=90°. ∴ . ∴ GH=AG. ∴ CG=CH+GH=AG+BG. 8.如图,在正方形ABCD中,E是BC边上一点,连接AE,延长CB至点F,使BF=BE,过点F作FH⊥AE于点H,射线FH分别交AB、CD于点M、N,交对角线AC于点P,连接AF. (1)依题意补全图形; (2)求证:∠FAC=∠APF; (3)判断线段FM与PN的数量关系,并加以证明. 答案:(1)补全图如图所示. (2)证明∵正方形ABCD, ∴∠BAC=∠BCA=45°,∠ABC=90°, ∴∠PAH=45°-∠BAE. ∵FH⊥AE. ∴∠APF=45°+∠BAE. ∵BF=BE, ∴AF=AE,∠BAF=∠BAE. ∴∠FAC=45°+∠BAF. ∴∠FAC=∠APF. (3)判断:FM=PN. 证明:过B作BQ∥MN交CD于点Q, ∴MN=BQ,BQ⊥AE. ∵正方形ABCD, ∴AB=BC,∠ABC=∠BCD=90°. ∴∠BAE=∠CBQ. ∴△ABE≌△BCQ. ∴AE=BQ. ∴AE=MN. ∵∠FAC=∠APF, ∴AF=FP. ∵AF=AE, ∴AE=FP. ∴FP=MN. ∴FM=PN. 9.如图所示,点P位于等边的内部,且∠ACP=∠CBP. (1) ∠BPC的度数为________°; (2) 延长BP至点D,使得PD=PC,连接AD,CD. ①依题意,补全图形; ②证明:AD+CD=BD; (3) 在(2)的条件下,若BD的长为2,求四边形ABCD的面积. 解:(1)120°. ----------------------------2分 D (2)①∵如图1所示. ②在等边中,, ∴ ∵ ∴ ∴ ∴ ∵ ∴为等边三角形. ∵ ∴ 在和中, ∴. ∴ ∴-----------------------------------------4分 (3)如图2,作于点,延长线于点. ∵ ∴ ∴ ∴ 又由(2)得, -----------------------------------7分 10.如图1,在等边三角形ABC中,CD为中线,点Q在线段CD上运动,将线段QA绕点Q顺时针旋转,使得点A的对应点E落在射线BC上,连接BQ,设∠DAQ=α (0°<α<60°且α≠30°). (1)当0°<α<30°时, ①在图1中依题意画出图形,并求∠BQE(用含α的式子表示); ②探究线段CE,AC,CQ之间的数量关系,并加以证明; (2)当30°<α<60°时,直接写出线段CE,AC,CQ之间的数量关系. 图1 备用图 解:(1)①. ………………………………………………………………………… 1分 ② 0≤≤.……………………………………………………………… 2分 (2)设直线与x轴,y轴的交点分别为点A,点B,可得, . ∴ ,,. 由0≤≤,作直线. ①如图13,当⊙D与x轴相切时,相应的圆心满足题意,其横坐标取到最大值.作轴于点, 可得∥OB,. ∵ ⊙D的半径为1, 图13 ∴ . ∴ ,. ∴ . ②如图14,当⊙D与直线相切时, 相应的圆心满足题意,其横坐标取到最小值. 作轴于点,则⊥OA. 图14 设直线与直线的交点为F. 可得,OF⊥AB.则. ∵ ⊙D的半径为1, ∴ . ∴ . ∴ , . ∴ . 由①②可得,的取值范围是≤≤. ………………………………………… 5分 图15 (3)画图见图15. .……………………………… 7分 11.如图,在等边中, 分别是边上的点,且 , ,点与点关于对称,连接,交于. (1)连接,则之间的数量关系是 ; (2)若,求的大小; (用的式子表示) (3)用等式表示线段和之间的数量关系,并证明. (1); (2)解:连接,, ∵是等边三角形, ∴. ∵, ∴. ∵点与点关于对称, ∴,. ∴. 由(1)知. ∴,,在以为圆心,为半径的圆上. ∴. (3).理由如下: 连接,延长,交于点, ∵是等边三角形, ∴,. ∵点与点关于对称, ∴,. ∴. ∴. 设, 则. ∴. ∴. ∴. 由(2)知. ∴. ∴,. 四边形中,. ∴. ∴是等边三角形. ∴,. ∵, ∴. 在与中, ∴. ∴. ∵, ∴. 12.如图,在△ABC中,AB=AC,∠BAC=90°,M是BC的中点,延长AM到点D,AE= AD,∠EAD=90°,CE交AB于点F,CD=DF. (1)∠CAD= 度; (2)求∠CDF的度数; (3)用等式表示线段和之间的数量关系,并证明. 解:(1)45 ……………………………………………………………1分 (2)解:如图,连接DB. ∵°,是的中点, ∴∠BAD=∠CAD=45°. ∴△BAD≌△CAD. ………………………………2分 ∴∠DBA=∠DCA,BD = CD. ∵CD=DF, ∴BD=DF. ………………………………………3分 ∴∠DBA=∠DFB=∠DCA. ∵∠DFB+∠DFA =180°, ∴∠DCA+∠DFA =180°. ∴∠BAC+∠CDF =180°. ∴∠CDF =90°. ………………………………………4分 (3)CE=CD. ……………………………………5分 证明:∵°, ∴∠EAF=∠DAF=45°. ∵AD=AE, ∴△EAF≌△DAF. …………………………………6分 ∴DF=EF. 由②可知,CF=. …………………………7分 ∴CE=CD. 13.如图,正方形ABCD中,点E是BC边上的一个动点,连接AE,将线段AE绕点A逆时针旋转90°,得到AF,连接EF,交对角线BD于点G,连接AG. (1)根据题意补全图形; (2)判定AG与EF的位置关系并证明; (3)当AB = 3,BE = 2时,求线段BG的长. 解:(1)图形补全后如图…………………1分 (2)结论:AG⊥EF. …………………2分 证明:连接FD,过F点FM∥BC,交BD的延长线于点M. ∵四边形ABCD是正方形, ∴AB=DA=DC=BC,∠DAB=∠ABE=∠ADC=90°, ∠ADB=∠5=45°. ∵线段AE绕点A逆时针旋转90°,得到AF, ∴AE=AF,∠FAE=90°. ∴∠1=∠2. ∴△FDA≌△EBA. …………………3分 ∴∠FDA=∠EBA=90°,FD=BE. ∵∠ADC=90°, ∴∠FDA+∠ADC=180°。 ∴点F、D、C三点共线. ∴∠ADB=∠3=45°. ∵FM∥BC, ∴∠4=∠5=45°, ∴FM=FD, ∴FM=BE. ∵∠FGM=∠EGB,FM=BE,∠4=∠5, ∴△FMG≌△EGB. ∴FG=EG. ∵AE=AF, ∴AG⊥FE. ………………4分 (3) 解:如图,DB与FE交于点G. ∵AB=3,BE=2, ∴DC=3,CE=1,FD=2. ∴Rt△DAB中,DB=3. ∵四边形ABCD是正方形, ∴DH∥BC, ∴,即, ∴DH=. ∴,即, ∴BG=. ………………7分 14.在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P. (1)若点N是线段MB的中点,如图1. ① 依题意补全图1; ② 求DP的长; (2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求 CE的长. 解:(1)①如图1,补全图形. ………………… 1分 ② 连接AD,如图2. 在Rt△ABN中, ∵∠B=90°,AB=4,BN=1, ∴. ∵线段AN平移得到线段DM, ∴DM=AN=, AD=NM=1,AD∥MC, ∴△ADP∽△CMP. ∴. ∴.………………… 3分 (2)连接,如图3. 由平移知:∥,且=. ∵, ∴. ∴∥,且=. ∴四边形是平行四边形. ∴∥. ∴. 又∵, ∴. ∵∥, ∴. 又∵是的中点,且, ∴. ∴(舍负). ∴. ∴.………………… 7分 (2)法二,连接AD,如图4. 设CE长为x, ∵线段AB移动到得到线段DE, ∴,AD∥BM. ∴△ADP∽△CMP. ∴. ∵MQ=DP, ∴. ∵△QBM∽△QAD, ∴. 解得. ∴. ………………… 7分 15.如图,在△ABC中,AB=AC>BC,BD 是AC边上的高,点C关于直线BD的对称点为点E,连接BE. (1) ①依题意补全图形; ②若∠BAC=,求∠DBE的大小(用含的式子表示); (2) 若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长. (1)解:①如图. ……………………… 1分 ②∵ AB=AC,∠BAC=, ∴ ∠ABC=∠ACB=90°-. ∵点C关于直线BD的对称点为点E,BD 是AC边上的高. ∴ BD⊥CE,CD=DE. ∴ BE=BC. ∴ ∠BEC=∠ACB=90°-. …………………… 2分 ∴∠DBE=.……………… 3分 (2)解:作FG⊥AC于G, ∵BD⊥CE,∴FG∥BD ∵点F是BE中点,∴EG=DG.∴…………4分 ∵DE=2AE,∴AE=EG=DG.……………… 5分 设AE=EG=DG=x,则CD=DE=2x,AC=5x,∴AB=AC=5x. ∴BD=4x. ∵BD=4,∴x =1.……………… 6分 ∴AG=2. ∵=2, ∴AF=.……………… 7分查看更多