2012年乌鲁木齐中考数学试卷

2012年乌鲁木齐中考数学试卷

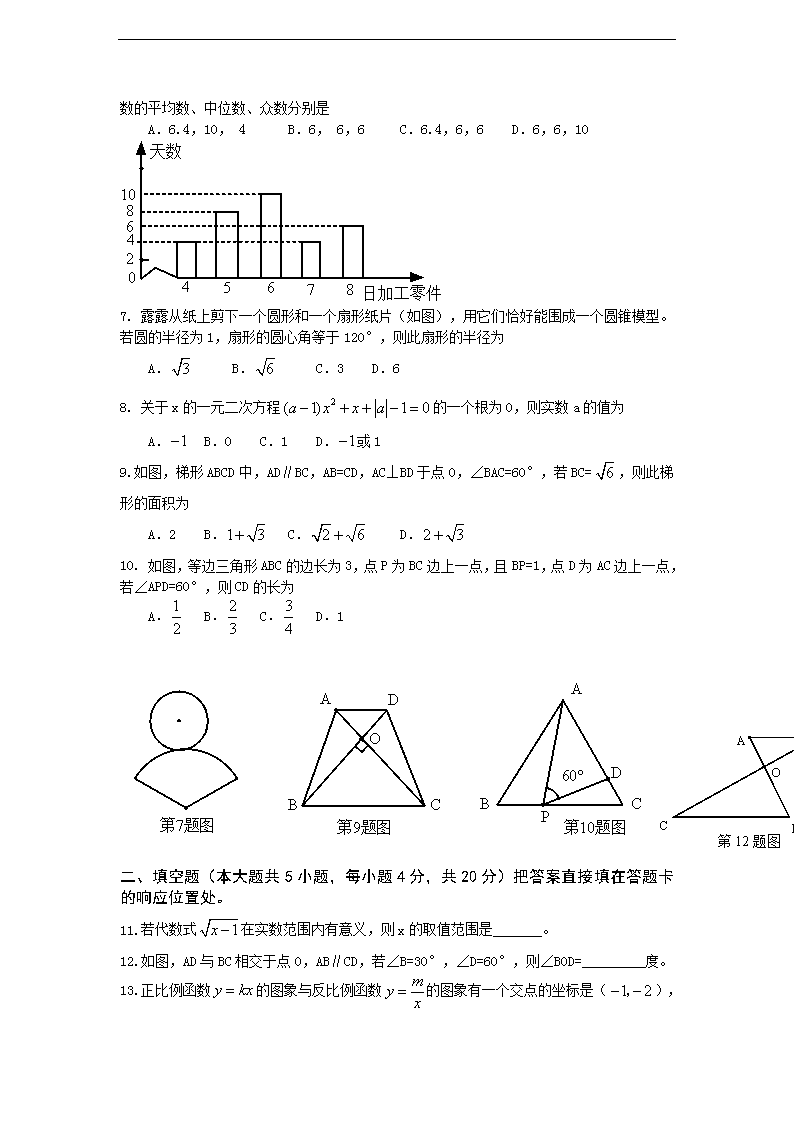
‎2011年乌鲁木齐市初中毕业生学业水平测试 数学试卷(问卷)‎ 注意事项：‎ ‎ 1.本卷共4页．满分l50分，考试时间120分钟、考试时可使用计算器。‎ ‎ 2.答题前，考生须将自己的姓名、准考证号、考场号．座位号填写在本试卷指定的位置上。‎ ‎ 3。选择题的每小题选出答案后．用2B铅笔把答提卡上对应题目的替案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试卷上，非选择题必须使用0．5毫米的黑色字迹的签字笔在答题卡上书写，字体工整．笔迹清楚．‎ ‎ 4. 非选择题必须按照题号顺序在答题卡上各题目的答题区域内作答。超出答题区域或在其它题的答题区域内书写的答案无效。在草稿纸、本试卷上答题无效：‎ ‎ 5.作图可先用2B铅笔绘出图．确定后必须用0.5毫米的黑色字迹的签字笔描黑，‎ ‎ 6.考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题（本大题共l0小题，每小题4分．共40分)每题的选项中只有一项符合题目要求 ‎1. 下列实数中．是无理数的为 ‎ A． 0 B． C． 3.14 D．‎ ‎2. 如图，在数轴上点A，B对应的实数分别为a．b．则有 A． B． C． D．‎ ‎3.下列运算正确的是 ‎ A． B． C． D．‎ ‎4.甲仓库与乙仓库共存粮450 吨、现从甲仓库运出存粮的60％．从乙仓库运出存粮的40％．结果乙仓库所余的粮食比甲仓库所余的粮食多30 吨。若设甲仓库原来存粮x吨．乙仓库原来存粮y吨，则有 ‎ A． B． ‎ C． D．‎ ‎5.将直线向右平移l个单位后所得图象对应的函数解析式为 ‎ A． B． C． D．‎ ‎6‎ ‎．右面的条形统计图描述了某车间供热那日加工零件数的情况，则这些供热那日加工零件数的平均数、中位数、众数分别是 A．6.4，10， 4 B．6， 6，6 C．6.4，6，6 D．6，6，10‎ ‎7. 露露从纸上剪下一个圆形和一个扇形纸片（如图），用它们恰好能围成一个圆锥模型。若圆的半径为1，扇形的圆心角等于120°，则此扇形的半径为 ‎ A． B． C．3 D．6‎ ‎8. 关于x的一元二次方程的一个根为0，则实数a的值为 A． B．0 C．1 D．或1‎ ‎9. 如图，梯形ABCD中，AD∥BC，AB=CD，AC⊥BD于点O，∠BAC=60°，若BC=，则此梯形的面积为 A．2 B． C． D．‎ ‎10. 如图，等边三角形ABC的边长为3，点P为BC边上一点，且BP=1，点D为AC边上一点，若∠APD=60°，则CD的长为 A． B． C． D．1‎ 第12题图 二、填空题（本大题共5小题，每小题4分，共20分）把答案直接填在答题卡的响应位置处。‎ ‎11.若代数式在实数范围内有意义，则x的取值范围是_______。‎ ‎12.如图，AD与BC相交于点O，AB∥CD，若∠B=30°，∠D=60°，则∠BOD=_________度。‎ ‎13.正比例函数的图象与反比例函数的图象有一个交点的坐标是（‎ ‎），则另一个交点的坐标为________。‎ ‎14.某居民小区为了了解本小区100户居民家庭的平均月使用塑料袋的数量情况，随机调查了10户居民家庭月使用塑料袋的数量，结果如下（单位：只）‎ ‎ 65 70 85 74 86 78 74 92 82 94‎ 根据此统计情况，估计该小区这100户居民家庭平均月使用塑料袋为________只。‎ ‎15.按如下程序进行运算：‎ 并规定，程序运行到“结果是否大于65”为一次运算，且运算进行4次才停止。则可输入的整数x的个数是_________‎ 三、解答题（本大题Ⅰ-Ⅴ，共9小题，共90分）解答时应在答题卡上的相应位置处写出文字说明。‎ Ⅰ.（本体满分15分，第16题7分，第17题8分）‎ ‎16．先化简．再求值：，其中。‎ ‎17.解方程：‎ Ⅱ.(本题满分30分．第l8题8分．第l9题l2分．第20题10分)‎ ‎18. 如入，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D。‎ 求证：△BEC≌△CDA ‎ 19．某商场销售一种进价为20元／台的台灯，经调查发现，该台灯每天的销售量w(太)与销售单价x(元)满足，‎ 设销售这种台灯每天的利润为y（元）。‎ ‎ （1）求y与x之间的函数关系式；‎ ‎ （2）当销售单价定为多少元时．每天的利润最大？最大利润是多少？‎ ‎（3）在保证销售量尽可能大的前提下．该商场每天还想获得150元的利润．应将销售单价定为多少元？‎ ‎20.如图，在ABCD中，∠DAB=60°，AB=2AD，点E、F分别是AB、CD的中点，过点A作AG∥BD，交CB的延长线于点G。‎ ‎（1）求证：四边形DEBF是菱形；‎ ‎（2）请判断四边形AGBD是什么特殊四边形？并加以证明。‎ Ⅲ.(本题满分23分．第21题l2分，第22题ll分)‎ ‎2l.在一个袋子中，有完全相同的4张卡片，把它们分别编号为l，2，3，4。‎ ‎ （1）从袋子中随机取两张卡片．求取出的卡片编号之和等于4的概率：‎ ‎ （2）先从袋子中随机取一张卡片，记该卡片的编号为a，然后将其放回，再从袋中随机取出一张卡片，级该卡片的编号为b，求满足的概率。‎ ‎22．某校课外活动小组，在距离湖面7米高的观测台A处，看湖面上空一热气球P的仰角为37°，看P在湖中的倒影P’的俯角为53°，（P’为P关于湖面的对称点），请你计算出这个热气球P距湖面的高度PC约为多少米？‎ 注：sin37°≈，cos37°≈，tan37°≈;‎ Sin53°≈，cos53°≈，tan53°≈‎ Ⅳ.(本题满分10分)‎ ‎23.小王从A地前往B地，到达后立刻返回，他与A地的距离y（千米）和所用的时间x（小时）之间的函数关系如图所示。‎ ‎（1）小王从B地返回A地用了多少小时？‎ ‎（2）求小王出发6小时后距A地多远？‎ ‎（3）在A、B之间友谊C地，小王从去时途经C地，到返回时路过C地，共用了2小时20分，求A、C两地相距多远？‎ Ⅴ.（本题满分12分）‎ ‎24.如图，在△ABC中，∠B=90°，AB=6米，BC=8米，动点P以2米/秒得速度从A点出发，沿AC向C移动，同时，动点Q以1米/秒得速度从C点出发，沿CB向B移动。当其中有一点到达终点时，他们都停止移动，设移动的时间为t秒。‎ ‎（1）①当t=2.5秒时，求△CPQ的面积；‎ ‎ ②求△CPQ的面积S（平方米）关于时间t（秒）的函数关系式；‎ ‎（2）在P、Q移动的过程中，当△CPQ为等腰三角形时，写出t的值；‎ ‎（3）以P为圆心，PA为半径的圆与以Q为圆心，QC为半径的圆相切时，求出t的值。‎ ‎2011年乌鲁木齐市初中毕业生学业水平测试 数学答案 一、 选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D A C C B B C A D B 二、 填空题 ‎11. 12. 90 13. 14. 80 15. 4‎ 三、 解答题 ‎16. 解：原式=，当时，原式=‎ ‎17. ‎ ‎18. 证明略 ‎19. 解：（1）‎ ‎（2）∵‎ ‎∴当x=30时，最大利润为元。‎ ‎（3）由题意，，即 解得。‎ 又销售量随单价增大而减小，故当x=25时，既能保证销售量大，又可以每天获得150元的利润。‎ ‎20. （1）证明略。‎ ‎ （2）四边形AGBD是矩形。理由略。‎ ‎21.（1） （2）P（）=‎ ‎22. 25米 ‎23. 解：（1）小王从B地返回A地用了4小时。‎ ‎（2）小王出发6小时，∵6>3，可知小王此时在返回途中。‎ 于是，设DE所在直线的解析式为，由图象可得：‎ ‎，解得 ‎∴DE所在直线的解析式为 当x=6时，有 ‎∴小王出发6小时后距A地60千米。‎ ‎（3）设AD所在直线的解析式为，易求 ‎∴AD所在直线的解析式为 设小王从C到B用了小时，则去时C距A的距离为 返回时，从B到C用了（）小时，‎ 这时C距A的距离为 由，解得 故C距A的距离为米 ‎24. 解：在Rt△ABC中，AB=6米，BC=8米，∴AC=10米 由题意得：AP=2t，CQ=10-2t ‎（1）①过点P作PD⊥BC于D。‎ ‎∵t=2.5，AP=2×2.5=5，QC=2.5‎ ‎∴PD=AB=3，∴S=×QC×PD=3.75‎ ‎②过点Q作QE⊥PC于点E 易知Rt△QEC∽Rt△ABC，∴，QE=‎ ‎∴S=‎ ‎（2）当秒（此时PC=QC），秒（此时PQ=QC），或秒（此时PQ=PC）△CPQ为等腰三角形；‎ ‎（3）过点P作PF⊥BC于点F，则有△PCF∽△ACB ‎∴，即 ‎∴PF=，FC=‎ 则在Rt△PFQ中，‎ 当⊙P与⊙Q外切时，有PQ=PA+QC=3t，此时 整理得：，解得 故⊙P与⊙Q外切时，；‎ 当⊙P与⊙Q内切时，有PQ=PA-QC=t，此时 整理得：，解得 故⊙P与⊙Q内切时