中考数学专题复习平移旋转与对称学生版

中考数学专题复习平移旋转与对称学生版

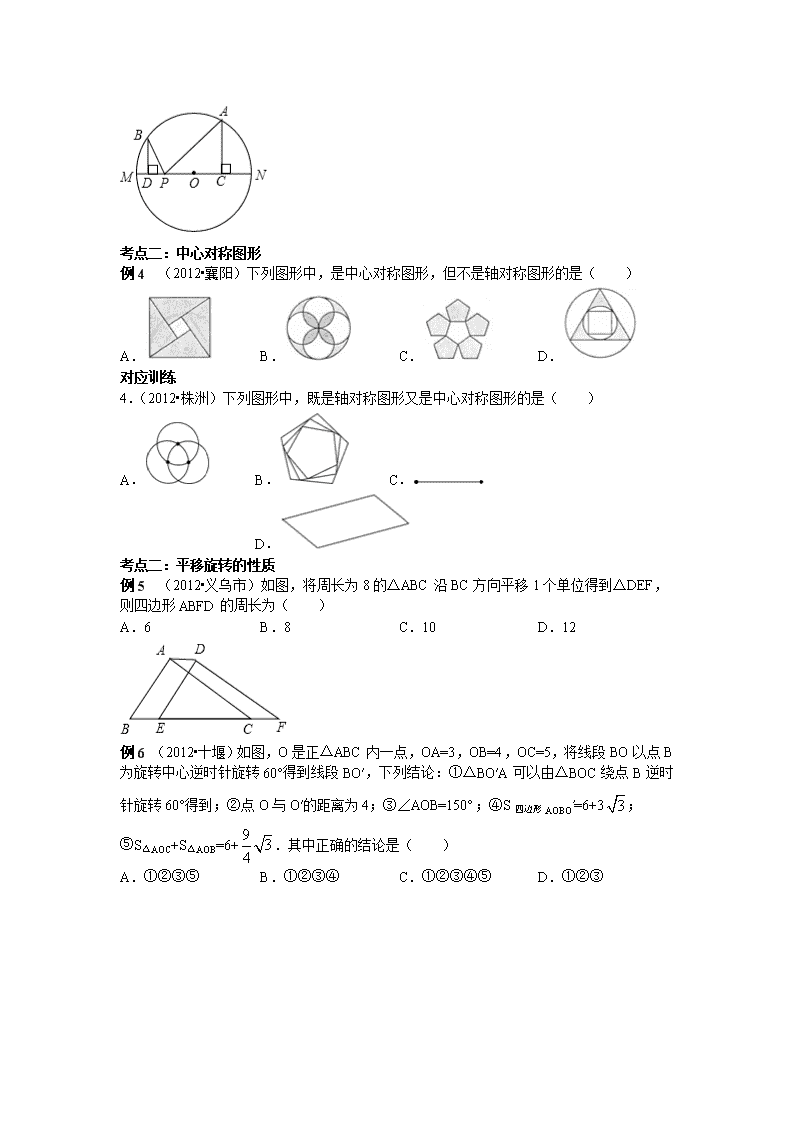
‎2013年中考数学专题复习 第二十六讲 平移、旋转与对称 ‎【基础知识回顾】‎ 一、 轴对称与轴对称图形：‎ ‎ 1、轴对称：把一个图 形沿着某一条直线翻折过去，如果它能够与另一个图形 那么就这说两个图形成轴对称，这条直线叫 ‎ ‎2、轴对称图形：如果把一个图形沿着某条直线对折，直线两旁的部分能够互相 那么这个图形叫做轴对称图形 ‎3、轴对称性质：⑴关于某条直线对称的两个图形 ‎ ‎⑵对应点连接被对称轴 ‎ ‎【名师提醒：1、轴对称是指 个图形的位置关系，而轴对称图形是指 各具有特殊形状的图形 ‎2、对称轴是 而不是线段，轴对称图形的对称轴不一定只有一条】‎ 二、图形的平移与旋转：‎ ‎ 1、平移：⑴定义：在平面内，把某个图形沿着某个 移动一定的 这样的图形运动称为平移 ‎⑵性质：Ⅰ平移不改变图形的 与 ，即平移前后的图形 ‎ ‎ Ⅱ平移前后的图形对应点连得线段平行且 ‎ ‎【名师提醒：平移作图的关键是确定平移的 和 】‎ ‎2、旋转：⑴定义：在平面内，将一个图形绕一个定点沿某个方向旋转一个 ，这样的图形运动称为旋转，这个点称为 转动的 称为旋转角 ‎⑵旋转的性质：Ⅰ：旋转前后的图形 ‎ ‎ Ⅱ：旋转前后的两个圆形中，对应点到旋转中心的距离都 ，每对对应点与旋转中心的连线所成的角度都是旋转角旋转角都 ‎ ‎【名师提醒：1、旋转作用的关键是确定 、 和 ，‎ ‎2、一个图形旋转一定角度后如果能与自身重合，那么这个图形就是旋转对称图形】‎ 三、中心对称与中心对称图形：‎ ‎1、中心对称：在平面内，一个图形绕某一点旋转1800能与自身重合它能与另一个图形 就说这两个图形关于这个点成中心对称，这个点叫做 ‎ ‎2、中心对称图形：一个图形绕着某点旋转 后能与自身重合，这种图形叫中心对称图形，这个点叫做 ‎ ‎3、性质：在中心对称的两个图形中，对称点的连线都经过 且被 平分 ‎【名师提醒：1、中心对称是指一个图形的位置关系，而中心对称图形是指一个具有特殊形状的图形 ‎2、常见的轴对称图形有 、 、 、 、 、 等，常见的中心对称图形有 、 、 、 、 、 等 ‎3、所有的正n边形都是 对称圆形里有四条对称轴，边数为偶数的正多边形，又是 对称图形 ‎4、注意圆形的各种变换在平面直角坐标系中的运用】‎ ‎【典型例题解析】‎ ‎ 考点一：轴对称图形 例1 （2012•柳州）娜娜有一个问题请教你，下列图形中对称轴只有两条的是（　　）‎ A． B． C． D． 圆 等边三角形 矩形 等腰梯形 例2 （2012•成都）如图，在平面直角坐标系xOy中，点P（-3，5）关于y轴的对称点的坐标为（　　）‎ A．（-3，-5） B．（3，5） C．（3．-5） D．（5，-3）‎ 对应训练 ‎1. （2012•宁波）下列交通标志图案是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎2．（2012•沈阳）在平面直角坐标系中，点P（-1，2）关于x轴的对称点的坐标为（　　）‎ A．（-1，-2） B．（1，-2） C．（2，-1） D．（-2，1）‎ 考点二：最短路线问题 例3 （2012•黔西南州）如图，抛物线y= x2+bx-2与x轴交于A、B两点，与y交于C点，且A（-1，0），点M（m，0）是x轴上的一个动点，当MC+MD的值最小时，m的值是（　　）‎ A． B． C． D．‎ 对应训练 ‎3. （2012•贵港）如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是 ．‎ 考点二：中心对称图形 例4 （2012•襄阳）下列图形中，是中心对称图形，但不是轴对称图形的是（　　）‎ A． B． C． D．‎ 对应训练 ‎4．（2012•株洲）下列图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ 考点二：平移旋转的性质 例5 （2012•义乌市）如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（　　）‎ A．6 B．‎8 ‎C．10 D．12‎ 例6 （2012•十堰）如图，O是正△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO′=6+3；⑤S△AOC+S△AOB=6+．其中正确的结论是（　　）‎ A．①②③⑤ B．①②③④ C．①②③④⑤ D．①②③‎ 对应训练 ‎5.（2012•莆田）如图，△A′B′C′是由△ABC沿射线AC方向平移‎2cm得到，若AC=‎3cm，则A′C= 1‎ cm．‎ ‎6．（2012•南通）如图Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，且AC在直线l上，将△ABC绕点A顺时针旋转到①，可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=2+ ；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=3+ ；…按此规律继续旋转，直到点P2012为止，则AP2012等于（　　）‎ A．2011+671 B．2012+‎671‎ C．2013+671 D．2014+671‎ 考点四：图形的折叠 例7 （2012•遵义）如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为（　　）‎ ‎　 A． 3 B． ‎2‎ C． 2 D． 2‎ 例8 （2012•天津）已知一个矩形纸片OACB，将该纸片放置在平面直角坐标洗中，点A（11，0），点B（0，6），点P为BC边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP=t． ‎ ‎ （Ⅰ）如图①，当∠BOP=30°时，求点P的坐标； （Ⅱ）如图②，经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，若AQ=m，试用含有t的式子表示m； （Ⅲ）在（Ⅱ）的条件下，当点C′恰好落在边OA上时，求点P的坐标（直接写出结果即可）．‎ 对应训练 ‎7．（2012•资阳）如图，在△ABC中，∠C=90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC=6，NC=，则四边形MABN的面积是（　　）‎ ‎　 A． B． C． D． ‎ ‎8．（2012•深圳）如图，将矩形ABCD沿直线EF折叠，使点C与点A重合，折痕交AD于点E，交BC于点F，连接AF、CE， （1）求证：四边形AFCE为菱形； ‎ ‎（2）设AE=a，ED=b，DC=c．请写出一个a、b、c三者之间的数量关系式．‎ ‎【备考真题过关】‎ 一、选择题 ‎1．（2012•丽水）如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是（　　）‎ A．① B．② C．⑤ D．⑥‎ ‎2. （2012•重庆）下列图形中，是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎3. （2012•宜昌）在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（　　）‎ A． B． C． D．‎ ‎4．（2012•自贡）下列图形中，既是轴对称图形，又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎5．（2012•资阳）下列图形：①平行四边形；②菱形；③圆；④梯形；⑤等腰三角形；⑥直角三角形；⑦国旗上的五角星．这些图形中既是轴对称图形又是中心对称图形的有（　　）‎ A．1种 B．2种 C．3种 D．4种 ‎6．（2012•岳阳）岳阳楼是江南三大名楼之一，享有“洞庭天下水，岳阳天下楼”‎ 的盛名，从图中看，你认为它是（　　）‎ A．轴对称图形 B．中心对称图形 C．既是轴对称图形，又是中心对称图形 D．既不是轴对称图形，又不是中心对称图形 ‎7．（2012•十堰）点P（-2，3）关于x轴对称点的坐标是（　　）‎ A．（-3，2） B．（2，-3） C．（-2，-3） D．（2，3）‎ ‎8．（2012•深圳）已知点P（a-1，‎2a-3）关于x轴的对称点在第一象限，则a的取值范围是（　　）‎ A．a＜-1 B． C． D．‎ ‎9．（2012•孝感）如图，△ABC在平面直角坐标系中第二象限内，顶点A的坐标是（-2，3），先把△ABC向右平移4个单位得到△A1B‎1C1，再作△A1B‎1C1关于x轴对称图形△A2B‎2C2，则顶点A2的坐标是（　　）‎ A．（-3，2） B．（2，-3） C．（1，-2） D．（3，-1）‎ ‎10．（2012•南通）线段MN在直角坐标系中的位置如图所示，若线段M′N′与MN关于y轴对称，则点M的对应点M′的坐标为（　　）‎ A．（4，2） B．（-4，2） C．（-4，-2） D．（4，-2）‎ ‎12. （2012•遵义）把一张正方形纸片如图①、图②对折两次后，再如图③挖去一个三角形小孔，则展开后图形是（　　）‎ A． B． C． D．‎ ‎13．（2012•西宁）如图，E、F分别是正方形ABCD的边BC、CD上的点，BE=CF，连接AE、BF．将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF，则旋转角是（　　）‎ A．45° B．120° C．60° D．90°‎ ‎14．（2012•苏州）如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB=15°，则∠AOB′的度数是（　　）‎ A．25° B．30° C．35° D．40°‎ ‎15. （2012•台州）如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（　　）‎ A．1 B． C．2 D．‎ ‎16．（2012•兰州）如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（　　）‎ A．130° B．120° C．110° D．100°‎ ‎17．（2012•舟山）如图，已知△ABC中，∠CAB=∠B=30°，AB=2，点D在BC边上，把△ABC沿AD翻折使AB与AC重合，得△AB′D，则△ABC与△AB′D重叠部分的面积为（　　）‎ ‎　 A． B． C． 3﹣ D． ‎ ‎19．（2012•武汉）如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE=5，BF=3，则CD的长是（　　）‎ ‎　 A． 7 B． ‎8 ‎C． 9 D． 10‎ 二、填空题 ‎20．（2012•宁夏）点B（-3，4）关于y轴的对称点为A，则点A的坐标是 （3，4）‎ ‎．‎ ‎21．（2012•大庆）在直角坐标系中，C（2，3），C′（-4，3），C″（2，1），D（-4，1），A（0，a），B（a，O）（a＞0）． （1）结合坐标系用坐标填空． 点C与C′关于点 （-1，3）‎ 对称； ‎ 点C与C″关于点 （2，2）‎ 对称；‎ 点C与D关于点 （-1，2）‎ 对称； （2）设点C关于点（4，2）的对称点是点P，若△PAB的面积等于5，求a值．‎ ‎22.（2012•遵义）在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有 13‎ 种．‎ ‎24．（2012•莆田）点A、B均在由面积为1的相同小矩形组成的网格的格点上，建立平面直角坐标系如图所示．若P是x轴上使得|PA-PB|的值最大的点，Q是y轴上使得QA+QB的值最小的点，则OP•OQ= 5‎ ‎．‎ ‎25．（2012•玉林）如图，两块相同的三角板完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置，点C′在AC上，A′C′与AB相交于点D，则C′D= ．‎ ‎26．（2012•厦门）如图，点D是等边△ABC内的一点，如果△ABD绕点A逆时针旋转后能与△ACE重合，那么旋转了 60‎ 度．‎ ‎27．（2012•攀枝花）如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为 ．‎ ‎28．（2012•岳阳）如图，在Rt△ABC中，∠B=90°，沿AD折叠，使点B落在斜边AC上，若AB=3，BC=4，则BD= 　　．‎ ‎29．（2012•扬州）如图，将矩形ABCD沿CE折叠，点B恰好落在边AD的F处，如果，那么tan∠DCF的值是 ．‎ ‎20．（2012•台州）如图，将正方形ABCD沿BE对折，使点A落在对角线BD上的A′处，连接A′C，则∠BA′C=　 　度．‎ 三、解答题 ‎34.（2012•吉林）如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠，点O恰好落在 上点D处，折痕交OA于点C，求整个阴影部分的周长和面积．‎ ‎36. （2012•鸡西）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN （1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN= ∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明． （2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN= ∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明． ‎ ‎37. （2012•北京）在△ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2α得到线段PQ． （1）若α=60°且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D，请补全图形，并写出∠CDB的度数； （2）在图2中，点P不与点B，M重合，线段CQ的延长线于射线BM交于点D，猜想∠CDB的大小（用含α的代数式表示），并加以证明； （3）对于适当大小的α，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且 PQ=QD，请直接写出α的范围．‎