- 2021-05-13 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
闵行区初三数学中考二模卷及答案
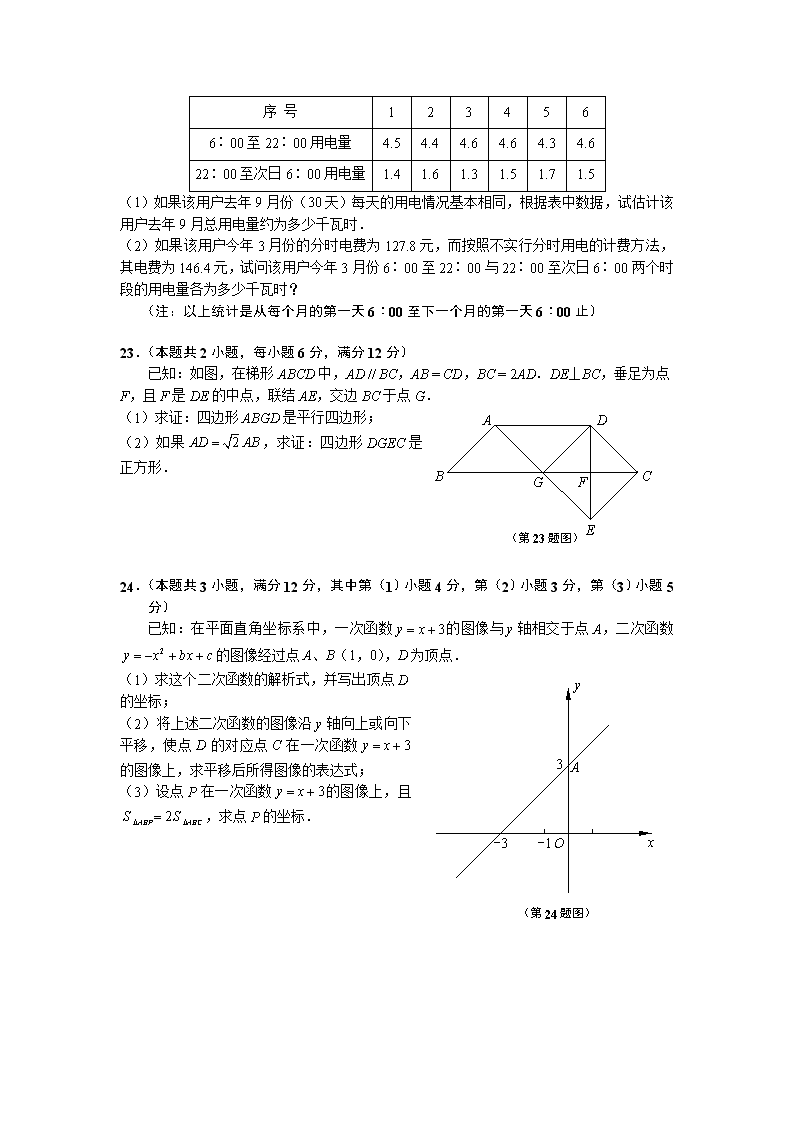
闵行区2012学年九年级质量调研考试 数学试卷 2013.04 一、选择题:(本大题共6题,每题4分,满分24分) 1.下列实数中,是无理数的是 (A)3.14; (B); (C); (D). 2.下列运算一定正确的是 (A); (B); (C); (D). 3.不等式组的解集是 (A); (B); (C); (D). 4.用配方法解方程时,配方后所得的方程是 (A); (B); (C); (D). 5.在△ABC与△A′B′C′中,已知AB = A′B′,∠A =∠A′,要使△ABC≌△A′B′C′,还需要增加一个条件,这个条件不正确的是 (A)AC = A′C′; (B)BC = B′C′; (C)∠B =∠B′; (D)∠C =∠C′. 6.下列命题中正确的是 (A)矩形的两条对角线相等; (B)菱形的两条对角线相等; (C)等腰梯形的两条对角线互相垂直; (D)平行四边形的两条对角线互相垂直. 二、填空题:(本大题共12题,每题4分,满分48分) 7.计算: . 8.因式分解: . 9.方程的实数根是 . 10.如果关于x的一元二次方程有两个实数根,那么m的取值范围是 . 11.一次函数的图像在y轴上的截距为 . 12.已知反比例()的图像经过点(2,-1),那么当时,y随x的增大而 .(填“增大”或“减小). 13.已知抛物线经过点(3,2),那么该抛物线的对称轴是直线 . 14.布袋中装有3个红球和3个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 . 15.如图,在平行四边形ABCD中,AC、BD相交于点O,如果,,那么 . 16.已知:⊙O1、⊙O2的半径长分别为2、5,如果⊙O1与⊙O2相交,那么这两圆的圆心距d的取值范围是 . 17.如图,在正方形ABCD中,E为边BC的中点,EF⊥AE,与边CD相交于点F,如果△CEF的面积等于1,那么△ABE的面积等于 . 18.如图,在Rt△ABC中,∠C = 90°,∠A = 50°,点D、E分别在边AB、BC上,将△BDE沿直线DE翻折,点B与点F重合,如果∠ADF = 45°,那么∠CEF = 度. A B C D E F (第17题图) A B C D O (第15题图) A C B D E F (第18题图) 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 先化简,再求值:,其中. 20.(本题满分10分) 解方程组: 21.(本题共2小题,满分10分,其中第(1)小题4分,第(2)小题6分) (第21题图) A F D E B C G 如图,在△ABC中,AB = AC,点D在边AB上,以点A为圆心,线段AD的长为半径的⊙A与边AC相交于点E,AF⊥DE,垂足为点F,AF的延长线与边BC相交于点G,联结GE.已知DE = 10,,. 求:(1)⊙A的半径AD的长; (2)∠EGC的余切值. 22.(本题共2小题,每小题5分,满分10分) 为了有效地利用电力资源,电力部门推行分时用电.即在居民家中安装分时电表,每天6∶00至22∶00用电每千瓦时0.61元,每天22∶00至次日6∶00用电每千瓦时0.30元.原来不实行分时用电时,居民用电每千瓦时0.61元.某户居民为了解家庭的用电及电费情况,于去年9月随意记录了该月6天的用电情况,见下表(单位:千瓦时). 序 号 1 2 3 4 5 6 6∶00至22∶00用电量 4.5 4.4 4.6 4.6 4.3 4.6 22∶00至次日6∶00用电量 1.4 1.6 1.3 1.5 1.7 1.5 (1)如果该用户去年9月份(30天)每天的用电情况基本相同,根据表中数据,试估计该用户去年9月总用电量约为多少千瓦时. (2)如果该用户今年3月份的分时电费为127.8元,而按照不实行分时用电的计费方法,其电费为146.4元,试问该用户今年3月份6∶00至22∶00与22∶00至次日6∶00两个时段的用电量各为多少千瓦时? (注:以上统计是从每个月的第一天6∶00至下一个月的第一天6∶00止) 23.(本题共2小题,每小题6分,满分12分) 已知:如图,在梯形ABCD中,AD // BC,AB = CD,BC = 2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. A B C D E F G (第23题图) (1)求证:四边形ABGD是平行四边形; (2)如果,求证:四边形DGEC是正方形. 24.(本题共3小题,满分12分,其中第(1)小题4分,第(2)小题3分,第(3)小题5分) 已知:在平面直角坐标系中,一次函数的图像与y轴相交于点A,二次函数的图像经过点A、B(1,0),D为顶点. A x y -1 -3 3 O (第24题图) (1)求这个二次函数的解析式,并写出顶点D的坐标; (2)将上述二次函数的图像沿y轴向上或向下平移,使点D的对应点C在一次函数的图像上,求平移后所得图像的表达式; (3)设点P在一次函数的图像上,且,求点P的坐标. 25.(本题共3小题,满分14分,其中第(1)小题4分,第(2)、(3)小题每小题5分) 如图,在平行四边形ABCD中,,,CE⊥AB,垂足为点E(点E在边AB上),F为边AD的中点,联结EF,CD. (1)如图1,当点E是边AB的中点时,求线段EF的长; (2)如图2,设,△CEF的面积等于y,求y与x的函数解析式,并写出函数定义域; (3)当时,∠EFD与∠AEF的度数满足数量关系:,其中k≥0,求k的值. A B C D E F (图2) A B C D E F (图1) (第25题图) A B C D E F 闵行区2012学年第二学期九年级质量调研考试 数学试卷参考答案及评分标准 一、选择题:(本大题共6题,每题4分,满分24分) 1.C;2.D;3.B;4.A;5.B;6.A. 二、填空题:(本大题共12题,每题4分,满分48分) 7.2;8.;9.;10.;11.3;12.增大;13.;14.; 15.;16.;17.4;18.35. 三、解答题:(本大题共7题,满分78分) 19.解:原式……………………………………………(4分) .…………………………………………………………………(2分) 当时,原式.…………………(4分) 20.解:由 ,得 ,. ………………(2分) 原方程组化为 ……………………………………(4分) 解这两个方程组,得原方程组的解是 …………………………………………………(4分) 21.解:(1)在⊙A中,∵ AF⊥DE,DE = 10, ∴ . …………………………………(1分) 在Rt△ADF中,由 , 得 ,.…………………………………………(1分) 利用勾股定理,得 . ∴ .解得 .……………………………(1分) ∴ AD = 13. …………………………………………………………(1分) (2)由(1),可知 .………………………………………(1分) ∵ , ∴ .………………………………………(1分) 在⊙A中,AD = AE. 又∵ AB = AC, ∴ .∴ DE // BC.…………………(1分) ∴ ,. ∴ AG = 36. ∴ .…………………………(1分) 在Rt△EFG中,.……………………………(1分) 即得 .………………………………………………(1分) 22.解:(1)6∶00至22∶00用电量: .……………………………(2分) 22∶00至次日6∶00用电量: .………………………………(2分) 所以 135 +45 = 180(千瓦时).……………………………………(1分) 所以,估计该户居民去年9月总用电量为180千瓦时. (2)根据题意,得该户居民5月份总用电量为 (千瓦时).(1分) 设该用户6月份6∶00至22∶00的用电量为x千瓦时,则22∶00至次日6∶00的用电量为(240 –x)千瓦时. 根据题意,得 .……………………(2分) 解得 .…………………………………………………………(1分) 所以 . …………………………………………………(1分) 答:该用户6月份6∶00至22∶00与22∶00至次日6∶00两个时段的用电量分别为180、60千瓦时. 23.证明:(1)∵ DE⊥BC,且F是DE的中点,∴ DC = EC. 即得 ∠DCF =∠ECF.……………………………………………(1分) 又∵ AD // BC,AB = CD,∴ ∠B =∠DCF,AB = EC. ∴ ∠B =∠ECF.∴ AB // EC.…………………………………(1分) 又∵ AB = EC,∴ 四边形ABEC是平行四边形.……………(1分) ∴ .………………………………………………(1分) ∵ BC = 2AD,∴ AD = BG.………………………………………(1分) 又∵ AD // BG,∴ 四边形ABGD是平行四边形.……………(1分) (2)∵ 四边形ABGD是平行四边形, ∴ AB // DG,AB = DG.…………………………………………(1分) 又∵ AB // EC,AB = EC,∴ DG // EC,DG = EC. ∴ 四边形DGEC是平行四边形.…………………………………(1分) 又∵ DC = EC,∴ 四边形DGEC是菱形.……………………(1分) ∴ DG = DC. 由 ,即得 .………………(1分) ∴ .∴ . ∴ 四边形DGEC是正方形. ……………………………………(2分) 24.解:(1)由 ,得 . ∴ 点A的坐标为A(0,3).………………………………………(1分) ∵ 二次函数的图像经过点A(0,3)、B(1,0), ∴ ……………………………………………………(1分) 解得 ∴ 所求二次函数的解析式为.……………………(1分) 顶点D的坐标为D(-1,4).…………………………………………(1分) (2)设平移后的图像解析式为. 根据题意,可知点C(-1,k)在一次函数的图像上, ∴ .…………………………………………………………(1分) 解得 .……………………………………………………………(1分) ∴ 所求图像的表达式为或.……(1分) (3)设直线与x轴交于点E. 由(2)得 C(-1,2). 又由 A(0,3),得 . 根据题意,设点P的坐标为P(m,m +3). ∵ △ABP与△ABC同高, 于是,当 时,得 .……………(1分) 此时,有两种不同的情况: (ⅰ)当点P在线段CA的延长线上时,得 ,且. 过点P作PQ1垂直于x轴,垂足为点Q1. 易得 .∴ .解得 .即得 . ∴ P1(2,5).………………………………………………………(2分) (ⅱ)当点P在线段AC的延长线上时,得 ,且. 过点P作PQ2垂直于x轴,垂足为点Q2. 易得 .∴ .解得 .即得 . ∴ P2(-2,1).………………………………………………………(2分) 综上所述,点P的坐标为(2,5)或(-2,1). 另解:(3)由(2)得 C(-1,2). 又由 A(0,3),得 . 根据题意,设点P的坐标为P(m,m +3). ∵ △ABP与△ABC同高, 于是,当 时,得 .……………(1分) ∴ . 即得 .………………………………………(1分) 解得 ,.………………………………………………(1分) ∴ m +3 = 5或1.……………………………………………………(1分) ∴ 点P的坐标为(2,5)或(-2,1).……………………………(1分) 25.解:(1)分别延长BA、CF相交于点P. 在平行四边形ABCD中,AD // BC,AD = BC.……………………(1分) 又∵ F为边AD的中点, ∴ .即得 PA = AB = 8.……………………(1分) ∵ 点E是边AB的中点,AB = 8,∴ . 即得 . ∵ CE⊥AB,∴ . ∴ .…………………………(1分) 在Rt△PEC中,,, ∴ .………………………………………………(1分) (2)在Rt△PEC中,,∴ . 由 BC = x,利用勾股定理 , 得 .即得 .………………………(1分) ∴ .∴ .…(1分) 于是,由 ,得 . ∴ .………………………………………(1分) ∴ ,.………………………………(2分) (3)在平行四边形ABCD中,AB // CD,CD = AB = 8,AD = BC = 16. ∵ F为边AD的中点,∴ .………………(1分) ∴ FD = CD.∴ .………………………………(1分) ∵ AB // CD,∴ ∠DCF =∠P. ∴ ∠DFC =∠P. ……………………………………………………(1分) 在Rt△PEC中,,, ∴ EF = PF.∴ ∠AEF =∠P =∠DFC. 又∵ ∠EFC =∠P +∠PEF = 2∠PEF. ……………………………(1分) ∴ ∠EFD =∠EFC +∠DFC = 2∠AEF +∠AEF = 3∠AEF. 即得 k = 3.……………………………………………………………(1分)查看更多