上海初三中考数学第题专项复习

上海初三中考数学第题专项复习

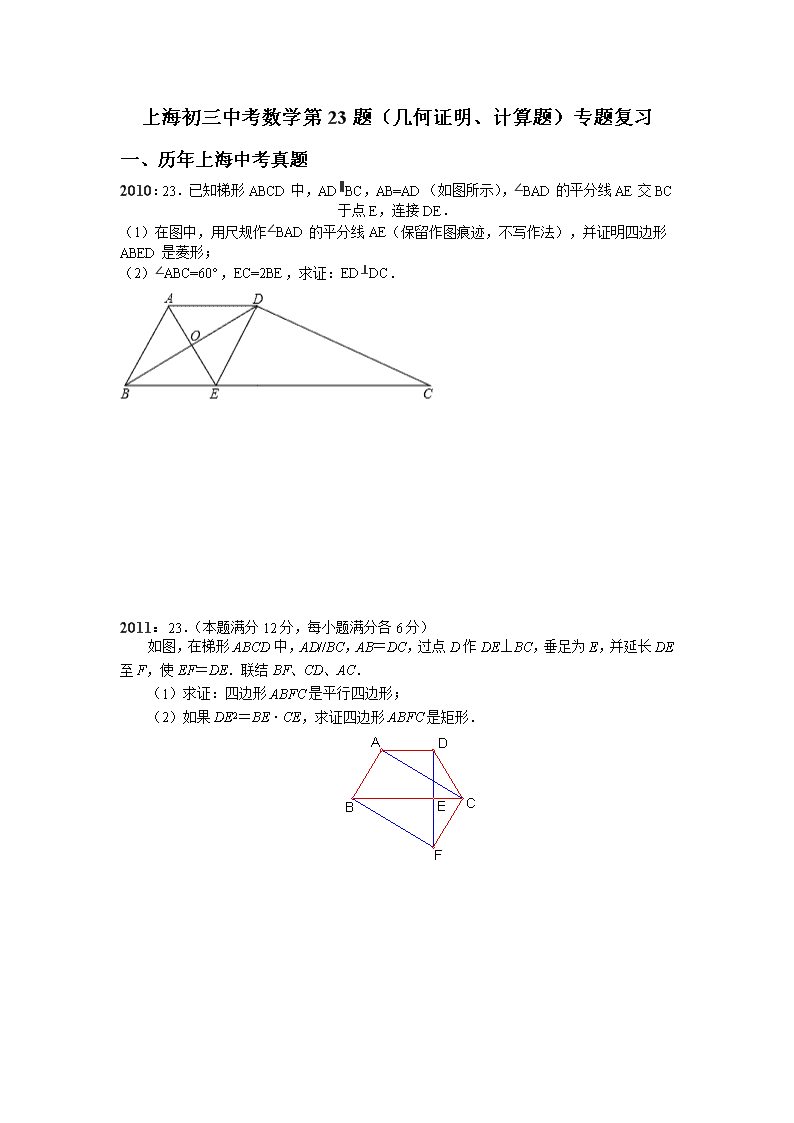
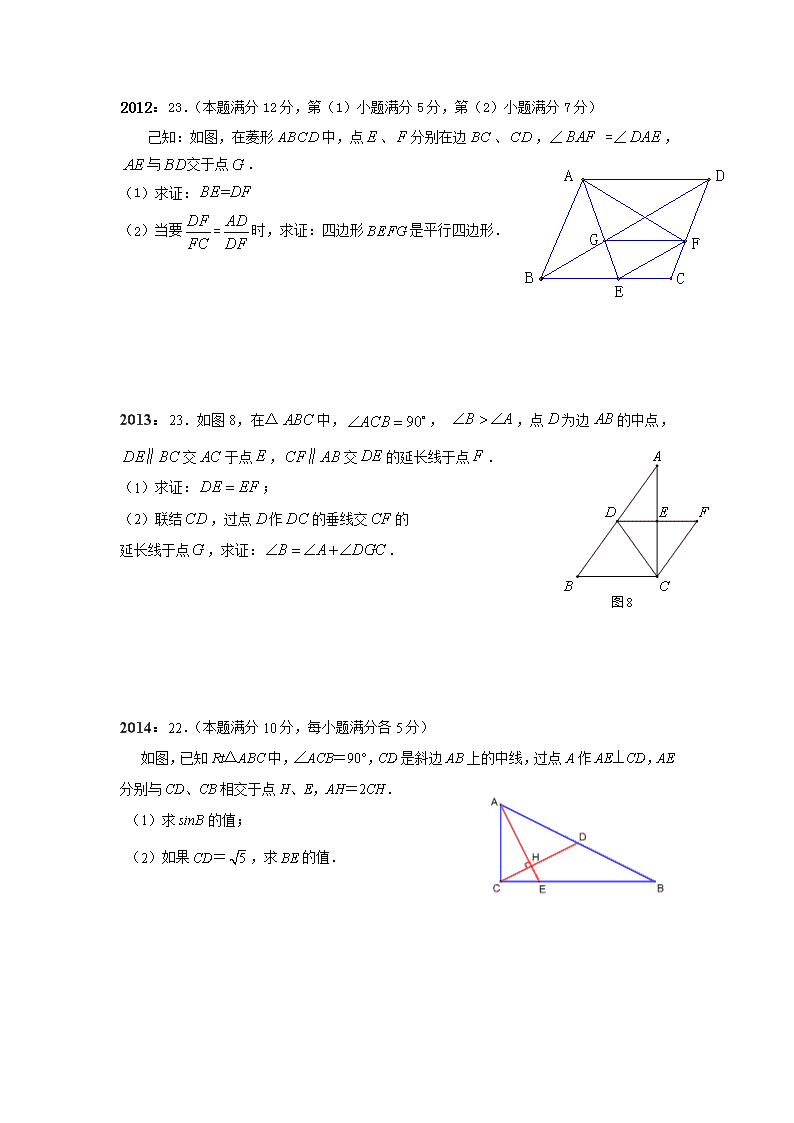
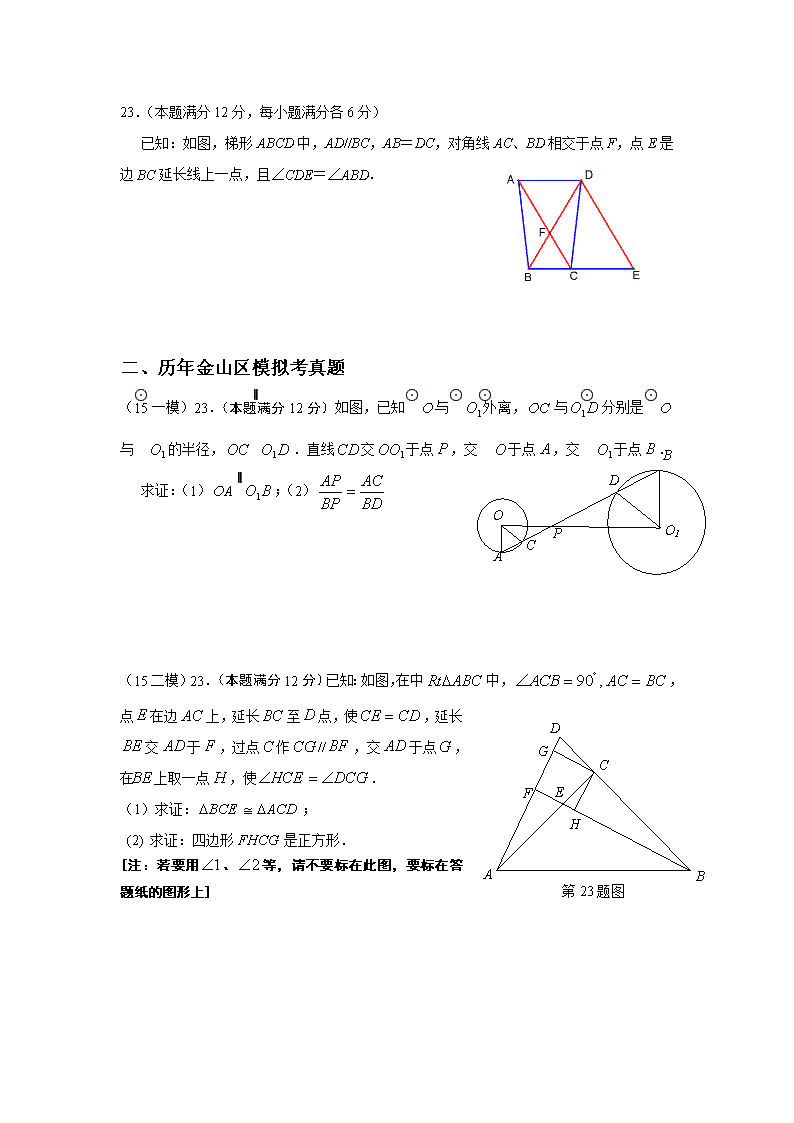
上海初三中考数学第23题（几何证明、计算题）专题复习 一、历年上海中考真题 ‎2010：23．已知梯形ABCD中，AD∥BC，AB=AD（如图所示），∠BAD的平分线AE交BC于点E，连接DE．‎ ‎（1）在图中，用尺规作∠BAD的平分线AE（保留作图痕迹，不写作法），并证明四边形ABED是菱形；‎ ‎（2）∠ABC=60°，EC=2BE，求证：ED⊥DC．‎ ‎2011：23．（本题满分12分，每小题满分各6分）‎ 如图，在梯形ABCD中，AD//BC，AB＝DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF＝DE．联结BF、CD、AC．‎ ‎（1）求证：四边形ABFC是平行四边形；‎ ‎（2）如果DE2＝BE·CE，求证四边形ABFC是矩形．‎ ‎2012：23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）‎ 己知：如图，在菱形中，点、分别在边、，∠ =∠，与交于点． ‎ ‎（1）求证：‎ ‎（2）当要=时，求证：四边形是平行四边形．‎ 图8‎ ‎2013：23．如图8，在△中，， ，点为边的中点，交于点，交的延长线于点．‎ ‎（1）求证：；‎ ‎（2）联结，过点作的垂线交的 延长线于点，求证：．‎ ‎2014：22．（本题满分10分，每小题满分各5分）‎ 如图，已知Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与CD、CB相交于点H、E，AH＝2CH．‎ ‎（1）求sinB的值；‎ ‎（2）如果CD＝，求BE的值．‎ ‎23．（本题满分12分，每小题满分各6分）‎ 已知：如图，梯形ABCD中，AD//BC，AB＝DC，对角线AC、BD相交于点F，点E是边BC延长线上一点，且∠CDE＝∠ABD．‎ 二、 历年金山区模拟考真题 ‎（15一模）23．（本题满分12分）O A C P D O1‎ B 如图，已知⊙与⊙外离，与分别是⊙与⊙的半径，∥．直线交于点，交⊙于点，交⊙于点．‎ 求证：（1）∥；（2）‎ G F E D B A C 第23题图 H ‎（15二模）23．（本题满分12分）已知：如图，在中中，,，点在边上，延长至点，使，延长交于，过点作//，交于点，在上取一点，使．‎ ‎（1）求证：；‎ ‎(2) 求证：四边形是正方形．‎ ‎[注：若要用、等，请不要标在此图，要标在答题纸的图形上]‎ ‎（09二模）23（本题满分10分）如图，等腰梯形ABCD中，AD∥BC，点E是AD延长线上一点，DE = BC.‎ D A B C ‎（第23题图）‎ E ‎（1）求证：∠E =∠DBC；‎ ‎（2）若等腰梯形ABCD的中位线长为6，∠E =，‎ 求等腰梯形ABCD的对角线的长。‎ 三、2015年中考题型展望 上海中考数学试卷的出题风格在23题上相对固定，旨在考察学生对于几何问题证明或者计算基本图形之间的综合掌握。题目难度主要以中档层次题目为主，一般不存在找不到思路的情况。若熟练掌握基本几何知识点，就能以不变应万变解答出此类中考问题。‎ 几何证明及计算 ‎ ‎（1）特殊三角形的边、角计算（2）特殊三角形的边、角计算。（3）特殊三角形、特殊四边形的性质应用（4）三角形中位线（5）全等三角形、相似三角形的判定和性质应用（6）正多边形的对称性问题（7）圆的垂径定理，圆的切线判定及性质（8）图形运动问题（平移、旋转、翻折）（9）几何图形与锐角三角比结合证明或计算（10）几何图形与函数结合证明或计算 ‎ ‎*相似三角形的性质的考察加大力度，主要考察学生的思维及能力解决。‎ 全等三角形的判定：‎ ‎①边角边公理（SAS） ②角边角公理（ASA） ③角角边定理（AAS） ④边边边公理（SSS）⑤斜边、直角边公理（HL）‎ 等腰三角形的性质：‎ ‎①等腰三角形的两个底角相等；‎ ‎②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（三线合一）‎ 等腰三角形的判定：有两个角相等的三角形是等腰三角形；‎ 直角三角形的性质：‎ ‎①直角三角形的两个锐角互为余角；②直角三角形斜边上的中线等于斜边的一半；‎ ‎③直角三角形的两直角边的平方和等于斜边的平方（勾股定理）；‎ ‎④直角三角形中角所对的直角边等于斜边的一半；‎ 直角三角形的判定：‎ ‎①有两个角互余的三角形是直角三角形；‎ ‎②如果三角形的三边长a、b 、c有下面关系，那么这个三角形是直角三角形（勾股定理的逆定理）。‎ ‎(4)四边形 多边形的内角和定理：n边形的内角和等于（n≥3，n是正整数）；‎ 平行四边形的性质：‎ ‎①平行四边形的对边相等；②平行四边形的对角相等；③平行四边形的对角线互相平分；‎ 平行四边形的判定：‎ ‎①两组对角分别相等的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；‎ ‎③对角线互相平分的四边形是平行四边形；④一组对边平行且相等的四边形是平行四边形。‎ 矩形的性质：（除具有平行四边形所有性质外）‎ ‎①矩形的四个角都是直角；②矩形的对角线相等；‎ 矩形的判定：①有三个角是直角的四边形是矩形；②对角线相等的平行四边形是矩形；‎ 菱形的特征：（除具有平行四边形所有性质外 ‎①菱形的四边相等；②菱形的对角线互相垂直平分，并且每一条对角线平分一组对角；‎ 菱形的判定：四边相等的四边形是菱形；‎ 正方形的特征：‎ ‎①正方形的四边相等；②正方形的四个角都是直角；‎ ‎③正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角；‎ 正方形的判定：‎ ‎①有一个角是直角的菱形是正方形；②有一组邻边相等的矩形是正方形。‎ 等腰梯形的特征:①等腰梯形同一底边上的两个内角相等 ②等腰梯形的两条对角线相等。‎ 等腰梯形的判定：①同一底边上的两个内角相等的梯形是等腰梯形；②两条对角线相等的梯形是等腰梯形。‎ 圆点与圆的位置关系（设圆的半径为r，点P到圆心O的距离为d）：‎ ‎①点P在圆上，则d=r，反之也成立； ②点P在圆内，则dr，反之也成立；‎ 圆心角、弦和弧三者之间的关系：在同圆或等圆中，圆心角、弦和弧三者之间只要有一组相等，可得到另外两组也相等 圆的确定：不在一直线上的三个点确定一个圆；‎ 垂径定理（及垂径定理的推论）：垂直于弦的直径平分弦，并且平分弦所对的两条弧；‎ 平行弦夹等弧：圆的两条平行弦所夹的弧相等；‎ 圆心角定理：圆心角的度数等于它所对弧的度数；‎ 圆心角、弧、弦、弦心距之间的关系定理及推论：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦的弦心距相等；‎ 推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦心距中有一组量相等，那么它们所对应的其余各组量分别相等；‎ 圆周角定理：圆周角的度数等于它所对的弧的度数的一半；‎ 圆周角定理的推论：直径所对的圆周角是直角，反过来，的圆周角所对的弦是直径；‎ 切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线；‎ 切线的性质定理：圆的切线垂直于过切点的半径；‎ 切线长定理：从圆外一点引圆的两条切线，这一点到两切点的线段相等，它与圆心的连线平分两切线的夹角；‎ 弧长计算公式：（R为圆的半径，n是弧所对的圆心角的度数，为弧长）‎ 扇形面积：（R为半径，n是扇形所对的圆心角的度数，为扇形的弧长）‎ ‎(6)尺规作图（基本作图、利用基本图形作三角形和圆）‎ 作一条线段等于已知线段，作一个角等于已知角；作已知角的平分线；作线段的垂直平分线；过一点作已知直线垂线；‎ 图形的相似比例的基本性质：如果，则，如果，则 相似三角形的设别方法：①两组角对应相等；②两边对应成比例且夹角对应相等；③三边对应成比例 相似三角形的性质：①相似三角形的对应角相等；②相似三角形的对应边成比例；‎ ‎③相似三角形的周长之比等于相似比；④相似三角形的面积比等于相似比的平方；‎ 相似多边形的性质：‎ ‎①相似多边形的对应角相等；②相似多边形的对应边成比例；‎ ‎③相似多边形的面积之比等于相似比的平方；‎ 口诀：人说几何很困难，难点就在辅助线。  辅助线，如何添？把握定理和概念。  还要刻苦加钻研，找出规律凭经验。  图中有角平分线，可向两边作垂线。  也可将图对折看，对称以后关系现。  角平分线平行线，等腰三角形来添。  角平分线加垂线，三线合一试试看。  线段垂直平分线，常向两端把线连。  要证线段倍与半，延长缩短可试验。  三角形中两中点，连接则成中位线。  三角形中有中线，延长中线等中线。  平行四边形出现，对称中心等分点。  梯形里面作高线，平移一腰试试看。  ‎ 平行移动对角线，补成三角形常见。  ‎ 证相似，比线段，添线平行成习惯。  等积式子比例换，寻找线段很关键。  直接证明有困难，等量代换少麻烦。  斜边上面作高线，比例中项一大片。  半径与弦长计算，弦心距来中间站。  圆上若有一切线，切点圆心半径连。  切线长度的计算，勾股定理最方便。  要想证明是切线，半径垂线仔细辨。  是直径，成半圆，想成直角径连弦。  弧有中点圆心连，垂径定理要记全。  圆周角边两条弦，直径和弦端点连。  弦切角边切线弦，同弧对角等找完。  ‎ 要想作个外接圆，各边作出中垂线。  ‎ 还要作个内接圆，内角平分线梦圆  如果遇到相交圆，不要忘作公共弦。  内外相切的两圆，经过切点公切线。  若是添上连心线，切点肯定在上面。  要作等角添个圆，证明题目少困难。  辅助线，是虚线，画图注意勿改变。  假如图形较分散，对称旋转去实验。  基本作图很关键，平时掌握要熟练。  解题还要多心眼，经常总结方法显。  切勿盲目乱添线，方法灵活应多变。  分析综合方法选，困难再多也会减。  虚心勤学加苦练，成绩上升成直线。‎ 几何图形线段长度计算三大方法： “勾股定理” “相似比例计算” “直角三角形中的三角函数