- 2021-05-10 发布 |
- 37.5 KB |
- 7页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考尺规作图题专题复习
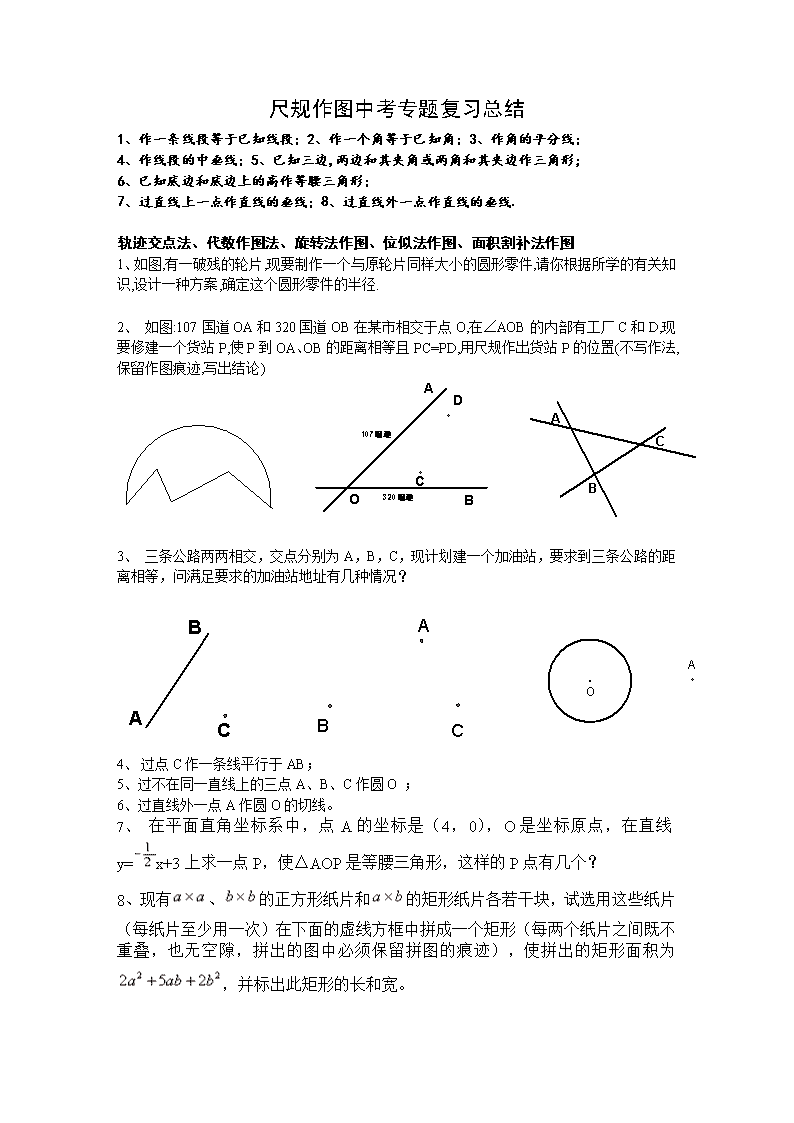
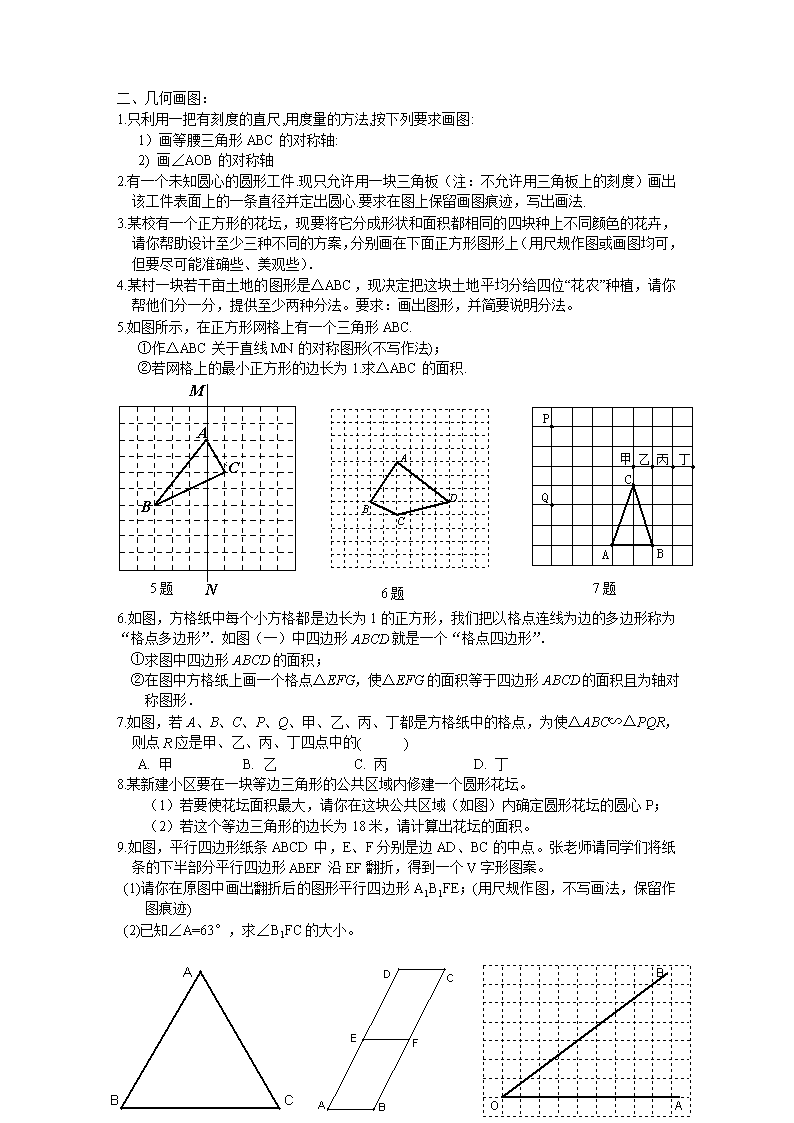
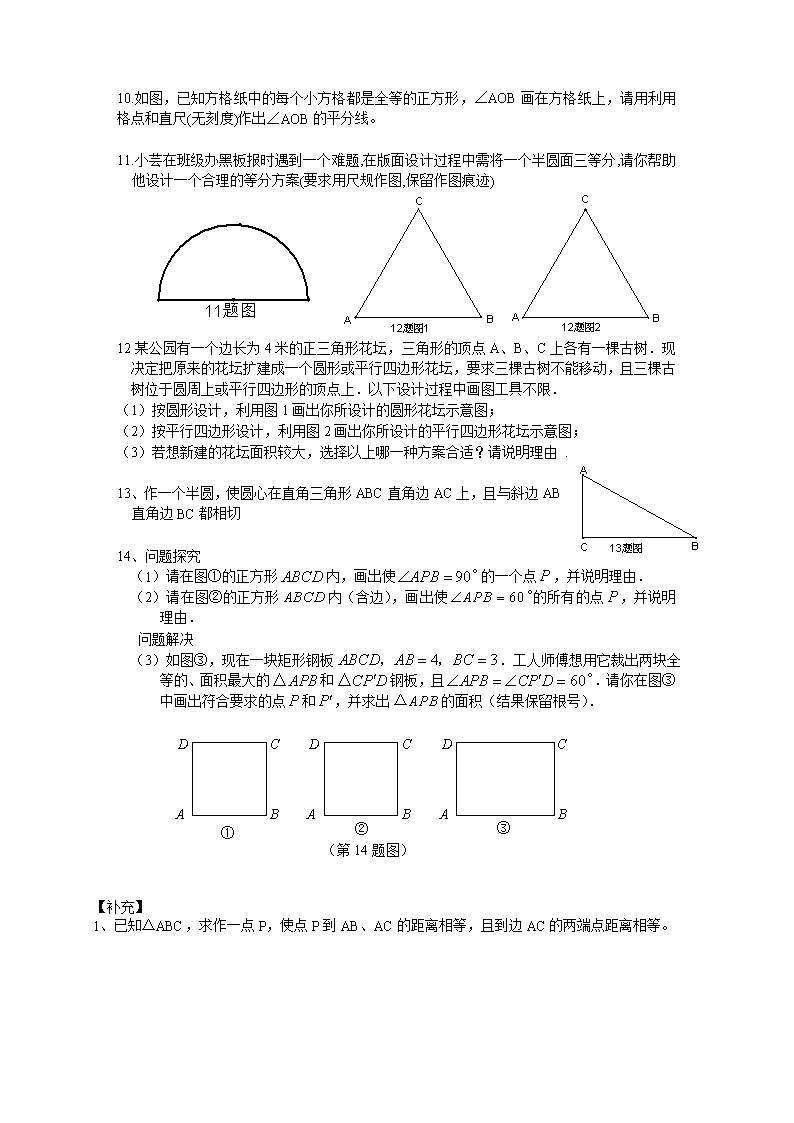
尺规作图中考专题复习总结 1、作一条线段等于已知线段;2、作一个角等于已知角;3、作角的平分线; 4、作线段的中垂线;5、已知三边,两边和其夹角或两角和其夹边作三角形; 6、已知底边和底边上的高作等腰三角形; 7、过直线上一点作直线的垂线;8、过直线外一点作直线的垂线. 轨迹交点法、代数作图法、旋转法作图、位似法作图、面积割补法作图 1、 如图,有一破残的轮片,现要制作一个与原轮片同样大小的圆形零件,请你根据所学的有关知识,设计一种方案,确定这个圆形零件的半径. 2、 如图:107国道OA和320国道OB在某市相交于点O,在∠AOB的内部有工厂C和D,现要修建一个货站P,使P到OA、OB的距离相等且PC=PD,用尺规作出货站P的位置(不写作法,保留作图痕迹,写出结论) 3、 三条公路两两相交,交点分别为A,B,C,现计划建一个加油站,要求到三条公路的距离相等,问满足要求的加油站地址有几种情况? 4、 过点C作一条线平行于AB; 5、过不在同一直线上的三点A、B、C作圆O ; 6、过直线外一点A作圆O的切线。 7、 在平面直角坐标系中,点A的坐标是(4,0),O是坐标原点,在直线y=x+3上求一点P,使△AOP是等腰三角形,这样的P点有几个? 8、现有、的正方形纸片和的矩形纸片各若干块,试选用这些纸片(每纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为,并标出此矩形的长和宽。 二、 几何画图: 1.只利用一把有刻度的直尺,用度量的方法,按下列要求画图: 1)画等腰三角形ABC的对称轴: 2) 画∠AOB的对称轴 2.有一个未知圆心的圆形工件.现只允许用一块三角板(注:不允许用三角板上的刻度)画出 该工件表面上的一条直径并定出圆心.要求在图上保留画图痕迹,写出画法. 3.某校有一个正方形的花坛,现要将它分成形状和面积都相同的四块种上不同颜色的花卉,请你帮助设计至少三种不同的方案,分别画在下面正方形图形上(用尺规作图或画图均可,但要尽可能准确些、美观些). 4.某村一块若干亩土地的图形是ΔABC,现决定把这块土地平均分给四位“花农”种植,请你帮他们分一分,提供至少两种分法。要求:画出图形,并简要说明分法。 5. 如图所示,在正方形网格上有一个三角形ABC. ①作△ABC关于直线MN的对称图形(不写作法); 6题 7题 A N B M C C 5题 ②若网格上的最小正方形的边长为1.求△ABC的面积. 6.如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图(一)中四边形ABCD就是一个“格点四边形”. ①求图中四边形ABCD的面积; ②在图中方格纸上画一个格点△EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形. 7.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的( ) A. 甲 B. 乙 C. 丙 D. 丁 8.某新建小区要在一块等边三角形的公共区域内修建一个圆形花坛。 (1)若要使花坛面积最大,请你在这块公共区域(如图)内确定圆形花坛的圆心P; (2)若这个等边三角形的边长为18米,请计算出花坛的面积。 9.如图,平行四边形纸条ABCD中,E、F分别是边AD、BC的中点。张老师请同学们将纸条的下半部分平行四边形ABEF沿EF翻折,得到一个V字形图案。 (1)请你在原图中画出翻折后的图形平行四边形A1B1FE;(用尺规作图,不写画法,保留作图痕迹) (2)已知∠A=63°,求∠B1FC的大小。 10题 9题 8题 10.如图,已知方格纸中的每个小方格都是全等的正方形,∠AOB画在方格纸上,请用利用格点和直尺(无刻度)作出∠AOB的平分线。 11.小芸在班级办黑板报时遇到一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助他设计一个合理的等分方案(要求用尺规作图,保留作图痕迹) 12某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限. (1)按圆形设计,利用图1画出你所设计的圆形花坛示意图; (2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图; (3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由 . 13、 作一个半圆,使圆心在直角三角形ABC直角边AC上,且与斜边AB直角边BC都相切 14、 问题探究 (1)请在图①的正方形内,画出使的一个点,并说明理由. (2)请在图②的正方形内(含边),画出使的所有的点,并说明理由. 问题解决 (3)如图③,现在一块矩形钢板.工人师傅想用它裁出两块全等的、面积最大的和钢板,且.请你在图③中画出符合要求的点和,并求出的面积(结果保留根号). D C B A ① D C B A ③ D C B A ② (第14题图) 【补充】 1、已知ΔABC,求作一点P,使点P到AB、AC的距离相等,且到边AC的两端点距离相等。 2、 如图,A、B、C三个小区中间有一块三角形的空地,现计划在这块空地上建一个超市,使得它到三个小区的距离相等,请你用尺规作图的方法确定超市所在位置。 3、如图,有分别过A、B两个加油站的公路、相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且P到两条公路、的距离也相等。请用尺规作图作出点P(不写作法,保留作图痕迹). 4、如图,A、B是两个蓄水池,都在河流a的同旁,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两池,问该站建在河边哪一点,可使所修的渠道最短,试在图中画出该点(不写作法,但要保留作图痕迹) 5、如图,A、B是两个小区,都在公路a的同旁,为了方便小区居民乘车,要在路边建一个车站牌,使得站牌到A、B两地的距离相等,问该站建在路边哪一点,试在图中画出该点(不写作法,但要保留作图痕迹) 6、如图所示,∠ABC内有一点P,在BA、BC边上各取一点P1、P2,使△PP1P2的周长最小. B 草地 河 A 7、如图,A为马厩,B为帐篷,牧马人一天要从马厩牵出马,先到草地边牧马,再到河边饮马,然后回到帐篷。请你帮他确定这一天的最短路线。 8、如图,过的底边上一定点,,求作一直线,使其平分的面积. 9、如图:五边形可以看成是由一个直角梯形和一个矩形构成. ⑴ 请你作一条直线,使直线平分五边形的面积; ⑵ 这样的直线有多少条?请你用语言描述出这样的直线. 10、求作:一正方形,使得、在边上,在边上,在边上. 11、已知:直线、、,且. 求作:正,使得、、三点分别在直线、、上. 12、求作一正方形,使其面积等于已知的面积. 【分析】 设的底边长为,高为,关键是在于求出正方形的边长,使得,所以是与的比例中项. 13、只用圆规,不许用直尺,四等分圆周(已知圆心 14、如果花园形状是任意四边形ABCD,四边形内部有一条折线小路AEC刚好平分四边形面积,现在小区的物业公司想把折线小路修成直线小路,由于各种条件限制,小路要通过点A,并且只能修在AC和点E之间,同时还要平分四边形面积,请你帮助设计? 相关题目 有一块梯形状的土地,现要平均分给两个农户种植(即将梯形的面积两等分),试设计两种方案(平分方案画在备用图上),并给予合理的解释。 15、采用构图法建立一个网格,并在网格中 ①作一个三角形使其两边为无理数且其面积为6 ②画一个底边长是4,面积为8的等腰三角形 ③画一个面积是10的等腰三角形 16、在中,、、三边的长分别为、、,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图所示.这样不需求的高,而借用网格就能计算出它的面积. (1)请你将的面积直接填写在横线上.__________________ 17、点c为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC已知AB=5,DE=1,BD=8,设CD=X (1) 用含x的代数式表示AC+CE的长; (2) 请问点C满足什么条件时,求AC+CE最小值? (3) 根据(2)中的规律和结论,构图求代数式+的最小值。 18、过Y轴上A、B两点O Y A B O X ,在X轴上找一点C,使∠ACB最大。查看更多