天津市河西区中考数学一模试卷含答案word版
河西区2016--2017学年度初中毕业生学业考试模拟试卷(一)
数 学
考试时间:2017年5月3日
本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷第1页至第3页,第Ⅱ卷第4页至第8页。试卷满分120分。考试时间100分钟。
答卷前,请你务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回。
祝你考试顺利!
第Ⅰ卷
注意事项:
1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共12题,共36分。
一、选择题(本大题共12小题,每小题3分,共36分)
(1)计算(-3)-9的结果等于( )
(A)6 (B)12 (C)12 (D)6
(2)cos300的值是( )
(A) (B) (C) (D)
(3)下列图案中,可以看作中心对称图形的是( )
(4)第十三届全运会将于2017年8月在天津举行,其中足球比赛项目承办场地为团泊足球场,该足球场占地163000平方米,将163000用科学计数法表示应为( )
(A)163×103 (B)16.3×104 (C)1.63×105 (D)0.163×106
(5)如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
(6)分式方程的解为( )
(A)x=1 (B)x=2 (C)x=3 (D)x=-1
(7)等边三角形的边心距为,则该等边三角形的边长是( )
(A)3 (B)6 (C)2 (D)2
(8)数轴上点A表示a,将点A沿数轴向左移动3个单位得到点B,设点B所表示的数为x,则x可以表示
为( )
(A)a-3 (B)a+3 (C)3-a (D)3a+3
(9)在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5.从中随机摸出一个小球,其标号大于2的概率为( )
(A) (B) (C) (D)
(10)已知反比例函数y=当1
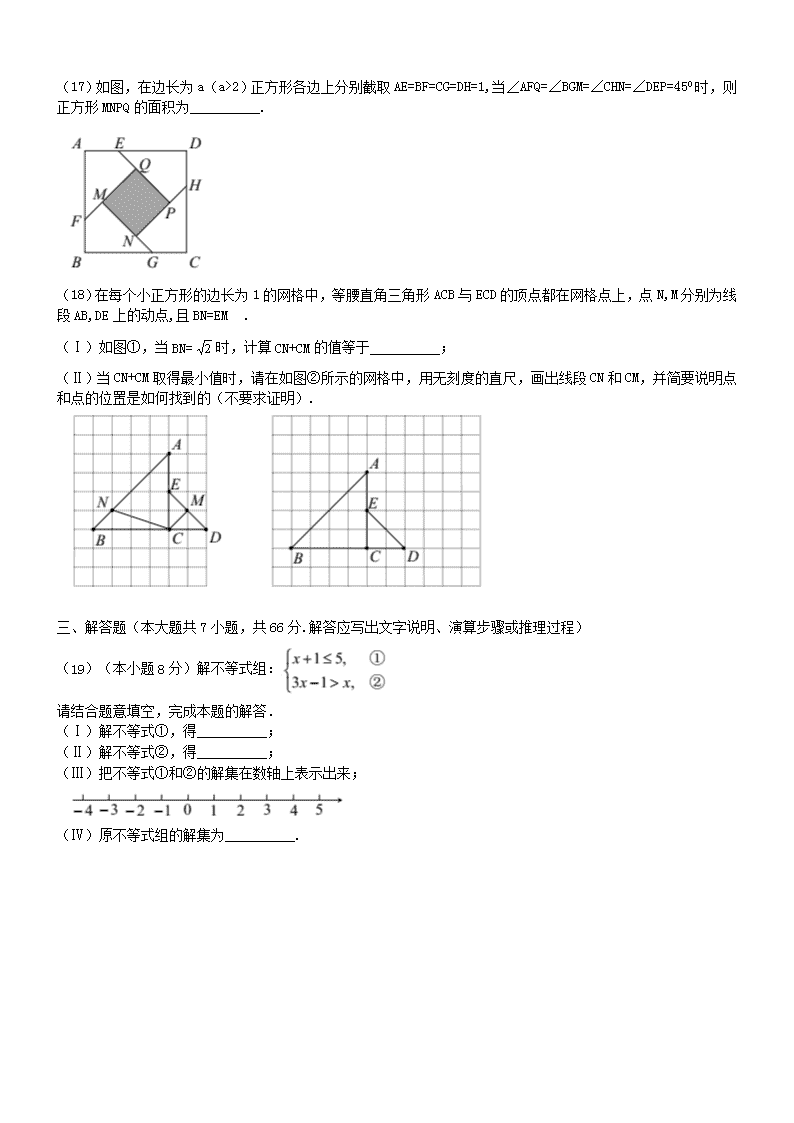
2)正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=450时,则正方形MNPQ的面积为__________.
(18)在每个小正方形的边长为1的网格中,等腰直角三角形ACB与ECD的顶点都在网格点上,点N,M分别为线段AB,DE上的动点,且BN=EM .
(Ⅰ)如图①,当BN=时,计算CN+CM的值等于__________;
(Ⅱ)当CN+CM取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段CN和CM,并简要说明点和点的位置是如何找到的(不要求证明).
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
(19)(本小题8分)解不等式组:
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得__________;
(Ⅱ)解不等式②,得__________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为__________.
(20)(本小题8分)为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如下面的统计图表:
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值__________;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
(21)(本小题10分)在⊙O中,AB为直径,C为⊙O上一点.
(Ⅰ)如图①,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=320,求∠P的大小;
(Ⅱ)如图②,D为优弧ADC上一点,且DO的延长线经过AC的中点E,连接DC与AB相交于点P,若∠CAB=160,
求∠DPA的大小.
(22)(本小题10分)解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.
(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A/C/的位置时,A/C/的长为__________m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=540,沿河岸MQ前行,在观景平台N处测得∠PNQ=730.已知PQ⊥MQ,MN=40m,求解放桥的全长PQ.(tan540≈1.4,tan730≈3.3,结果保留整数)
(23)(本小题10分)国庆期间,为了满足百姓的消费需求,某电器商店计划用170000元购进一批家电,这批家电的进价和售价如表:
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(Ⅰ)商店至多可以购买冰箱多少台?
(Ⅱ)购买冰箱多少台时,能使该商店销售完这批家电后获得的利润最大?最大利润为多少元?
(24)(本小题10分)如图,将一个矩形纸片ABCD,放置在平面直角坐标系中,A(0,0),B(4,0),D(0,3),
M是边CD上一点,将△ADM沿直线AM折叠,得到△ANM.
(Ⅰ)当AN平分∠MAB时,求∠DAM的度数和点M的坐标;
(Ⅱ)连接BN,当DM=1时,求△ABN的面积;
(Ⅲ)当射线BN交线段CD于点F时,求DF的最大值.(直接写出答案)
(25)(本小题10分)抛物线y=ax2+bx+c(a≠0)的图像经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=300 .
(Ⅰ)求抛物线的函数解析式;
(Ⅱ)若直线l:y=x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
(ⅰ)当m>0时,在线段AC上是否存在点P,使得P,D,E构成等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(ⅱ)以动直线l为对称轴,线段AC关于直线l的对称线段A/C/与该二次函数图象有交点,请直接写出m的取值范围.
数学参考答案
一、选择题:
(1)B (2)D (3)C (4) C (5) B (6)A (7)B (8)A (9)C (10) D
(11)D (12) D