2011中考模拟分类汇编 二次函数的图象和性质

2011中考模拟分类汇编 二次函数的图象和性质

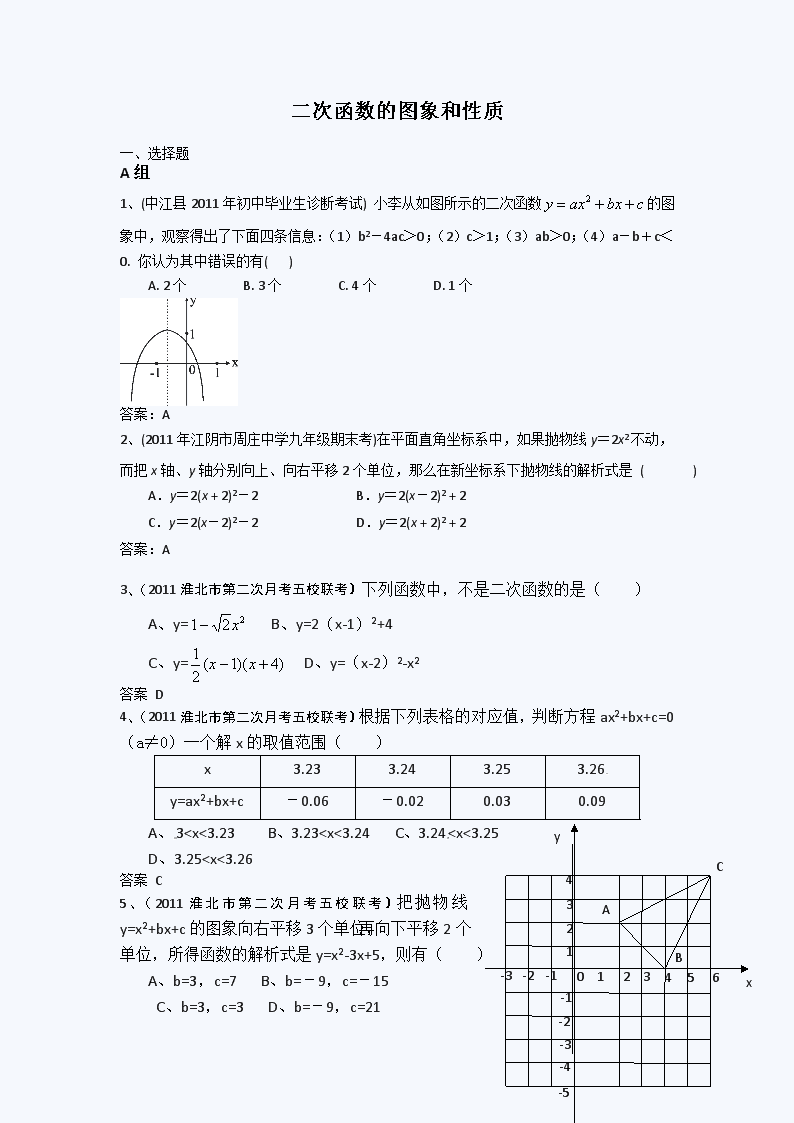
二次函数的图象和性质 一、 选择题 A组 ‎1、(中江县2011年初中毕业生诊断考试) 小李从如图所示的二次函数的图象中，观察得出了下面四条信息：（1）b2－‎4ac＞0；（2）c＞1；（3）ab＞0；（4）a－b＋c＜0. 你认为其中错误的有( )‎ ‎ A. 2个 B. 3个 C. 4个 D. 1个 答案：A ‎2、(2011年江阴市周庄中学九年级期末考)在平面直角坐标系中，如果抛物线y＝2x2不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是 ( ) ‎ A．y＝2(x + 2)2－2 B．y＝2(x－2)2 + 2 ‎ C．y＝2(x－2)2－2 D．y＝2(x + 2)2 + 2‎ 答案：A ‎3、（2011淮北市第二次月考五校联考）下列函数中，不是二次函数的是（ ）‎ A、y= B、y=2（x-1）2+4‎ C、y= D、y=（x-2）2-x2‎ 答案 D ‎4、（2011淮北市第二次月考五校联考）根据下列表格的对应值，判断方程ax2+bx+c=0（a≠0）一个解x的取值范围（ ）‎ x ‎3.23‎ ‎3.24‎ ‎3.25‎ ‎3.26‎ y=ax2+bx+c ‎－0.06‎ ‎－0.02‎ ‎0.03‎ ‎0.09‎ A、30,b>0,c>0 B.a<0,b<0,c0,c<0 D.a<0,b>0,c>o ‎ 答案：D ‎16．（2011北京四中模拟）己知二次函数，且则一定有（ ）.‎ A： B： ‎ C： D：‎ 答案：A ‎17．（2011年北京四中34模）已知抛物线，若点P（，5）与点关于该抛物线的对称轴对称，则点的坐标是（ ）‎ A．（0 ，5 ） B．（2 ，5） C．（3 ， 5 ） D．（4 ， 5 ）‎ 答案：D ‎18．（2011年北京四中34模）已知二次函数的图象如右图所示，下列结论：① ② ③④的实数)， 其中正确的结论有（ ）‎ A．1个 B．2个 C．3个 D．4个 答案：B ‎19．（2011年杭州市上城区一模）下列函数的图象，经过原点的是（ ）‎ A. B. C. D.‎ 答案：A 第7题 ‎20.（2011年杭州市模拟）二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为 ‎ 答案：D 第9题 ‎21. （2011年杭州市模拟）如图，在直角梯形中，∥，，，，动点同时从点出发，点沿、、运动到点停止，点沿运动到点停止，两点运动时的速度 都是/，而当点到达点时，点正好到达点．设点运动的时间为，的面积为．则能正确表示整个运动中关于的函数关系的大致图象是 A． B． C． D． ‎ 答案：B ‎22．（2011年海宁市盐官片一模）已知二次函数，则函数值y的最小值是（ ▲ ）‎ A. 3 B. ‎2 ‎ C. 1 D. －1‎ 答案：D ‎23．（赵州二中九年七班模拟）点E为正方形ABCD的BC边的中点，动点F在对角线AC上运动，连接BF、EF．设AF＝x，△BEF的周长为y，那么能表示y与x的函数关系的图象大致是（ ）‎ O x O O O x x x y y y y A B C D A B C D F E 答案：B x y ‎0‎ ‎24．（赵州二中九年七班模拟）二次函数的图像如图所示，则下列结论正确的是（ ）。‎ A. B.‎ C. D.0‎ 答案：D 一、 填空题 A组 ‎1、（2011重庆市纂江县赶水镇）在正方形的网格中，抛物线y1=x2+bx+c与直线y2=kx+m的图象如图所示，请你观察图象并回答：当－1”或“<”或“=”号）．‎ 答案：＜‎ ‎2、（重庆一中初2011级10—11学年度下期3月月考）小颖同学想用“描点法”画二次函数的图象，取自变量x的5个值，分别计算出对应的y值，如下表：‎ 1、 2、 ‎…‎ 3、 4、 5、 ‎0‎ 6、 ‎1‎ 7、 ‎2‎ 8、 ‎…‎ 9、 10、 ‎…‎ 11、 ‎11‎ 12、 ‎2‎ 13、 ‎－1‎ 14、 ‎2‎ 15、 ‎5‎ 16、 ‎…‎ 由于粗心，小颖算错了其中的一个y值，请你指出这个算错的y值所对应的x= ______．‎ 答案：2‎ ‎3、（2011年北京四中四模）抛物线的顶点坐标是_____.‎ 答案：（0，－3）‎ ‎4、(2011年江阴市周庄中学九年级期末考)抛物线的顶点坐标是________.‎ 答案：(3，－6) ‎ ‎5、（2011北京四中模拟6）把抛物线向上平移2个单位，那么所得抛物线与x轴 的两个交点之间的距离是 .‎ 答案：4‎ ‎6、（2011淮北市第二次月考五校联考）抛物线y=ax2+bx+c（a≠0）上两点，当x取-1与3时，y值相同，抛物线的对称轴是__________.‎ 答案 X＝1‎ ‎7．（淮安市启明外国语学校2010－2011学年度第二学期初三数学期中试卷）如图，菱形ABCD的三个顶点在二次函数y=ax2－2ax+ （a＜0）的图象上，点A、B分别是该抛物线的顶点和抛物线与y轴的交点，则点D的坐标为 ．‎ 第7题图 答案：（2，）‎ ‎8、（2011年北京四中模拟28）抛物线的顶点坐标是 ．‎ 答案：（0，-1）‎ ‎9、(2011浙江杭州模拟14)老师给出一个y关于x的函数，甲、乙、丙、丁四位同学各指出这个函数的一个性质：甲：函数图象不经过第三象限；乙：函数图象经过第一象限；丙：当x<2时，y随x的增大而减小；丁：当x<2时y>0.已知这四位同学叙述都正确。请写出满足上述所有性质的一个函数______________.‎ 答案： 答案不唯一.例如：‎ ‎10、(2011浙江杭州模拟15)甲、乙两位同学对问题“求函数的最小值”提出各自的想法。甲说：“可以用配方法，把它配成，所以函数的最小值为‎-2”‎。乙说：“我也用配方法，但我配成，最小值为‎2”‎。你认为__________（填写“甲对”、“乙对”、“甲、乙都对”或“甲乙都不对”）的。你还可以用________法等方法来解决．‎ 答案：乙 图象（答案不唯一）‎ ‎11、（2011年黄冈中考调研六）抛物线y＝7x2＋28x＋30的顶点坐标为 。‎ 答案 ‎12、已知关于x的函数y＝（m－1）x2＋2x＋m图像与坐标轴有且只有2个交点，则m＝ ‎ 答案：‎ ‎13.(河北省中考模拟试卷)抛物线y=（x+1）2-2的顶点坐标是 ．‎ 答案：(-1,-2)‎ B组 ‎1．（2011年三门峡实验中学3月模拟）抛物线向上平移2个单位，再向右平移1个单位后，得到的抛物线的解析式为____________．‎ 答案：或 ‎ 第2题 ‎2．（2011年三门峡实验中学3月模拟）如图，已知⊙P的半径为2，圆心P在抛物线上运动，当⊙P与轴相切时，圆心P的坐标为 . ‎ 答案：或 ‎3．（ 2011年杭州三月月考）将二次函数的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是 ▲ 。‎ 答案：‎ O x A y H C y=x2‎ ‎4．（2011 天一实验学校 二模）．如图，在第一象限内作射线OC,与x轴的夹角为30o,在射线OC上取一点A，过点A作AH⊥x轴于点H.在抛物线y=x2 (x>0)上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是 _______________ .‎ 源答案：(3，) ,(，) , (2，2) , (，)‎ ‎5．（2011浙江杭州育才初中模拟）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线。如图，点A、B、C、D分别是“蛋圆”与坐标轴的交点，点D的坐标为（0，-3）AB为半圆直径，半圆圆心M（1，0），半径为2，则“蛋圆”的抛物线部分的解析式为__________________。经过点C的“蛋圆”的切线的解析式为__________________。（08年益阳第20题）‎ 答案：y=x2-2x-3, y=-2x-3‎ ‎6．（2011年浙江杭州27模）我们知道，根据二次函数的平移规律，可以由简单的函数通过平移后得到较复杂的函数，事实上，对于其他函数也是如此。如一次函数，反比例函数等。请问可以由通过_________________________平移得到。‎ 答案：向右平移1个单位，再向上平移3个单位 第7题 ‎7. （2011年浙江省杭州市模2） 如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x2（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与△‎ AOH全等，则符合条件的点A的坐标是 .‎ 答案：(，)(，)(3，)(2，2)‎ ‎8.（安徽芜湖2011模拟）如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c>0的解集是 .‎ 答案: x＜-1或x>3 ‎ ‎9.（河南新乡2011模拟）已知抛物线与轴的一个交点为，则代数 式的值为＿＿＿＿＿＿＿．‎ 答案：2009‎ ‎10.（浙江杭州进化2011一模）老师给出一个y关于x的函数，甲、乙、丙、丁四位同学各指出这个函数的一个性质：甲：函数图象不经过第三象限；乙：函数图象经过第一象限；丙：当x<2时，y随x的增大而减小；丁：当x<2时y>0.已知这四位同学叙述都正确。请写出满足上述所有性质的一个函数______________.‎ 第11题图 答案：答案不唯一.例如： ‎ ‎11．（2011北京四中模拟）如图示：己知抛物线，关于轴对称，抛物线，关于轴对称。如果抛物线的解析式是，那么抛物线的解析式是 ‎ ‎12．（江西省九校2010—2011第一次联考）将抛物线向下平移1个单位，得到的抛物线是 ．‎ 答案：y＝2x2-1 ‎ ‎13．（北京四中2011中考模拟12）一个函数具有下列性质：①它的图象不经过第三象限；②图象经过点（－1，1）；③当时函数值随自变量x增大而增大.试写出一个满足上述三条性质的函数的解析式 。‎ 答案：等（写一个即可）‎ ‎14．（北京四中2011中考模拟13）把抛物线向上平移2个单位，那么所得抛物线与x轴的两个交点之间的距离是 .‎ 答案：；‎ ‎15．（北京四中2011中考模拟14）抛物线y=(k+1)x-9开口向下,且经过原点,则k=_____.‎ 答案：-3;‎ 一、 解答题 A组 ‎1、（衢山初中2011年中考一模）如图，在平面直角坐标系中，点A，B，C的坐标分别 为．‎ ‎（1）请在图中画出向下平移3个单位的像；‎ ‎（2）若一个二次函数的图象经过（1）中的三个顶点，‎ 求此二次函数的关系式．‎ x O y A C B 答案：20、（1）‎ x O y A ‎ C B A A A ‎ 　　　　　　　 ‎ ‎（2）由题意得的坐标分别是（0，-1），（3，-1），（2，0）‎ 设过点的二次函数的关系式为，则有 ‎ ‎ 解得 ‎ ‎∴二次函数的关系式为 ‎ ‎2、(中江县2011年初中毕业生诊断考试)‎ ‎ 如图，在平面直角坐标系中，开口向下的抛物线与x轴交于A、B两点，D是抛物线的顶点，O为坐标原点. A、B两点的横坐标分别是方程 的两根，且cos∠DAB＝.‎ ‎（1）求抛物线的函数解析式；‎ ‎（2）作AC⊥AD，AC交抛物线于点C，求点C的坐标及直线AC的函数解析式；‎ ‎（3）在（2）的条件下，在x轴上方的抛物线上是否存在一点P，使△APC的面积最大？如果存在，请求出点P的坐标和△APC的最大面积；如果不存在，请说明理由.‎ 答案：（10分）解：（1）解方程得，.‎ ‎∴A（－2，0），B（6，0）. ‎ 过D作DE⊥x轴于E， ∵D是顶点，‎ ‎∴点E是AB的中点，∴E（2，0）.‎ 在Rt△DAE中，∵cos∠DAB＝，∴∠DAE＝45°，‎ ‎∴AE＝DE＝4，∴D（2，4） ‎ ‎（由A、B、D三点坐标解出二次函数解析式，不论用顶点式、两根式还是一般式均可）‎ ‎∴抛物线的解析式为（或写成）. ‎ ‎（2）∵AC⊥AD，由（1）∠DAE＝45°得：‎ ‎∠BAC＝45°，△ACG是等腰直角三角形. ‎ ‎∴设C（a，b）（显然a＞0，b＜0），‎ 则b＝―a―2，即C（a，―a―2）‎ ‎∵点C在抛物线上，∴―a―2＝―（a―2）2＋4‎ a2―‎8a―20＝0‎ 解之得：a1＝10，a2＝－2（舍去）‎ ‎∴C（10，－12）‎ 设直线AC的方程为，代入A、C的坐标，得 ‎ 解之得：‎ ‎∴直线AC的解析式为y＝―x―2. ‎ ‎（3）存在点P（4，3），使S△APC最大＝54. ‎ ‎ 理由如下：‎ ‎ 作CG⊥x轴于G，PF∥y轴交x轴于Q，交AC于F. 设点P的横坐标是h，‎ ‎ 则G（10，0），P（h，），F（h，－h－2）‎ ‎ ∴PF＝ ‎ ‎ △PCF的高等于QG .‎ ‎ S△APC＝S△APF＋S△PCF ‎ ＝PF·AQ＋PF·QG ‎ ＝PF（AQ＋QG）＝PF·AG ‎ ‎ ＝‎ ‎ ＝‎ ‎ ∴当h＝4时，S△APC最大＝54. 点P的坐标为（4，3）. ‎ ‎3、（2011年北京四中四模）已知二次函数的图象经过点（－1，－5），（0，－4）和（1，1）.求这个二次函数的解析式.‎ 答案：设所求函数的解析式为把（―1，―5），（0，－4），（1，1）分别代入，得 ， 解这个方程组，得所求的函数的解析式为 ‎ ‎4、（2011北京四中模拟7）已知二次函数 ‎，它的图象与x轴只有一个交点，交点为A，与y轴交于点B，且AB=2 . (1)求二次函数解析式； (2)当b<0时，过A的直线y=x＋m与二次函数的图象交于点C，在线段BC上依次取D、E两点，若，试确定ÐDAE的度数，并简述求解过程。‎ 答案 解法一：(1)∵的图象与x轴只有一个交点 ‎ ‎ ∴一元二次方程＝0有两个相等的实数根 ‎ ‎ 由AB=2，得A与B不重合，又a>0 ∴c>0 ∴ac=1 ‎ ‎ ∴二次函数与x轴，y轴交点坐标为 ‎ 在RtDABO中， ‎ 把(1)代入(2)，解得 把 ‎ ‎ 二次函数解析式为 (2)当b<0时，由二次函数的解析式 ‎ 直线与二次函数图象交点C的坐标为 ‎ 过C点作CF︿x轴，垂足为F，可推得 AB=AC，ÐBAC=90°(如图所示) 在CF上截取CM=BD，连结EM、AM，则 可证DABD≌DACM 从而可证DDAE≌DMAE ‎ ‎ ∴∠1=∠2，∠DAE=∠EAM ∴∠DAM=∠BAC=90° ∴∠DAE=45° ‎ ‎5、（2011北京四中模拟8）如图，在直角坐标系xOy中，正方形OABC的边长为‎2cm ‎，点A、C分别在x轴、y轴的正半轴上。抛物线经过点B、C。‎ ‎（1）求抛物线的解析式；‎ ‎（2）点D、E分别是AB、BC上的动点，且点D从点A开始，以‎1cm/s的速度沿AB向点B移动，同时点E从点B开始，以‎1cm/s的速度沿BC向点C移动。运动t 秒（t≤2）后，能否在抛物线上找到一点P，使得四边形BEDP为平行四边形。如果能，请求出t 值和点P的坐标；如果不能，请说明理由。‎ 答案 ‎ ‎;能,,P ‎6、（2011淮北市第二次月考五校联考）已知，二次函数y=x2+bx+c的图象过点A（－1，0）和点B（3，0）两点，且与y轴交于点C，‎ ‎（1）求抛物线的解析式；‎ ‎（2）求△ABC的面积。‎ 答案 解：(1)y＝(x+1)(x-3)=x2-2x-3 ………………2分 ‎ (2)AB=3-(-1)=4 ………………4分 ‎ S△ABC=×4×3=6 ………………8分 ‎7、（2011淮北市第二次月考五校联考）丁丁推铅球的出手高度为‎1.6m，在如图所示的直角坐标系中，铅球运动路线是抛物线y=－0.1（x－k）2+2.5，求铅球的落点与丁丁的距离。‎ 答案 y=0.1 x2+0.2kx-0.1k2+2.5 ………………2分 ‎ -0.1k2+2.5=1.6 k＝±3 k＝3 ………………4分 ‎0.1（x－3）2+2.5=0 x1=－2(舍去) x2=8 ‎ 所以, 铅球的落点与丁丁的距离为‎8cm. ………………8分 ‎8．（淮安市启明外国语学校2010－2011学年度第二学期初三数学期中试卷）如图所示，在平面直角坐标系中，抛物线y=ax2+bx+3（a≠0）经过、两点，抛物线与y轴交点为C，其顶点为D，连接BD，点P是线段BD上一个动点（不与B、D重合），过点P作y轴的垂线，垂足为E，连接BE．‎ ‎（1）求抛物线的解析式，并写出顶点D的坐标；‎ ‎（2）如果P点的坐标为（x，y），△PBE的面积为s，求s与x的函数关系式，写出自变量x的取值范围，并求出s的最大值；‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ D y C B A P ‎2‎ E x O 第8题图 ‎（3）在（2）的条件下，当s取得最大值时，过点P作x的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为P＇，请直接写出P＇点坐标，并判断点P＇是否在该抛物线上．‎ 答案：（1）抛物线解析式为：． 顶点的坐标为． ‎ ‎（2）设直线解析式为：（），把两点坐标代入，‎ 得 解得．∴直线解析式为．‎ ‎，s=PE·OE ∴ ‎ ‎ ．‎ ‎∴当时，取得最大值，最大值为． ‎ ‎(E)‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ D y C B A P ‎2‎ x O F M H ‎（3）当取得最大值，，，∴．‎ ‎∴四边形是矩形．‎ 作点关于直线的对称点，连接．‎ 过作轴于，交轴于点．‎ 设，则．‎ 在中，由勾股定理，‎ ‎．解得．‎ ‎∵，∴．‎ 由，可得，．‎ ‎∴． ∴坐标． 不在抛物线上。‎ ‎9．（2011年浙江省杭州市城南初级中学中考数学模拟试题）已知二次函数的图象Q与x轴有且只有一个交点P，与y轴的交点为B（0，4），且ac＝b， ‎ ‎（1）求这个二次函数的解析式。‎ ‎（2）将一次函数y＝－3x的图象作适当平移，使它经过点P，记所得的图象为L，图象L与Q的另一个交点为C，请在y轴上找一点D，使得△CDP的周长最短。‎ 答案：（1）由B（0，4）得，c=4. ‎ Q与x轴的交点P（，0），‎ 由条件，得，所以=，即P（，0）．‎ 所以解得 所求二次函数的解析式为．‎ ‎（2）设图象L的函数解析式为y=x+b，因图象L过点P（，0），‎ O P B C x y P’‎ D 所以，即平移后所得一次函数的解析式为 y=．‎ 令=，‎ 解得，． ‎ 将它们分别代入y=，‎ 得，． ‎ 所以图象L与Q的另一个交点为C（，9）．‎ ‎∵点P（，0）关于y轴的对称点为点P’（2，0）‎ 则直线CP’的解析式为，且与y轴的交点为 即 ‎ ‎10．（2011年上海市卢湾区初中毕业数学模拟试题）已知：抛物线经过点，，且对称轴与轴交于点.‎ ‎（1）求抛物线的表达式；‎ ‎（2）如图，点、分别是轴、对称轴上的点，且四边形是矩形，点是上一点，将沿着直线翻折，点与线段上的点重合，求点的坐标；‎ ‎（3）在（2）的条件下，点是对称轴上的点，直线交于点，，求点坐标.‎ ‎(第3题图)‎ 答案：（1）由题意得 解，得∴.‎ ‎（2）∵与重合，，∴，，∴，又，‎ ‎∴，∵，∴∽，‎ ‎∴，‎ ‎∵四边形是矩形，∴，，‎ 设，则，∴，‎ ‎∴，解，得，∴，∴.‎ ‎（3）过点作，垂足为点.‎ ‎∵，∴，‎ ‎∵，，∴∥，‎ ‎∴，∴，∴.‎ ‎∴经过点，的直线的表达式为，‎ ‎∴.‎ ‎11．（2010－2011学年度河北省三河市九年级数学第一次教学质量检测试题）如图1，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为 (2,4)；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3.‎ ‎（1）求该抛物线的函数关系式；‎ ‎（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）. ‎ ‎① 当t=时，判断点P是否在直线ME上，并说明理由；‎ ‎② 设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．‎ 图2‎ B C O A D E M y x P N ‎·‎ 图1‎ B C O ‎(A)‎ D E M y x 答案：（1）‎ ‎（2）①点P不在直线ME上 ‎②依题意可知：P（,），N（，）‎ 当0＜t＜3时，以P、N、C、D为顶点的多边形是四边形PNCD，依题意可得：‎ ‎ =+=+=‎ ‎=‎ ‎∵抛物线的开口方向向下，∴当=，且0＜t＝＜3时，=‎ 当时,点P、N都重合，此时以P、N、C、D为顶点的多边形是三角形 依题意可得，==3‎ 综上所述，以P、N、C、D为顶点的多边形面积S存在最大值．‎ ‎12、(2011浙江杭州模拟15)‎ ‎_‎ M ‎_‎ A ‎_‎ B ‎_‎ O ‎_‎ x ‎_‎ y 第1题图 如图，在平面直角坐标系中，抛物线与直线交于点A、B，M是抛物线上一个动点，连接OM。‎ （1） 当M为抛物线的顶点时，求△OMB的面积；‎ （2） 当点M在抛物线上，△OMB的面积为10时，求点M的坐标；‎ （3） 当点M在直线AB的下方且在抛物线对称轴的右侧，M运动到何处时，△OMB的面积最大；‎ 答案：‎ ‎13、（2011年北京四中中考模拟20）‎ ‎(本题14分)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，)，C(0，)，点T在线段OA上(不与线段端点重合)，将纸片折叠，使点A落在射线AB上(记为点A′)，折痕经过点T，折痕TP与射线AB交于点P，设点T的横坐标为t，折叠后纸片重叠部分(图中的阴影部分)的面积为S；‎ ‎(1)求∠OAB的度数，并求当点A′在线段AB上时，S关于t的函数关系式；‎ ‎(2)当纸片重叠部分的图形是四边形时，求t的取值范围；‎ ‎(3)S存在最大值吗？若存在，求出这个最大值，并求此时t的值；若不存在，请说明理由。‎ y x O B C A T y x O B C A T 解：(1) ∵A，B两点的坐标分别是A(10，0)和B(8，)，‎ ‎ ∴，‎ ‎ ∴‎ ‎ 当点A´在线段AB上时，∵，TA=TA´，‎ ‎ ∴△A´TA是等边三角形，且，‎ ‎ ∴，，‎ A A´‎ B P T E C O y x ‎ ∴，‎ ‎ 当A´与B重合时，AT=AB=，‎ ‎ 所以此时。‎ ‎ (2)当点A´在线段AB的延长线，且点P在线段AB(不与B重合)上时，‎ ‎ 纸片重叠部分的图形是四边形(如图(1)，其中E是TA´与CB的交点)，‎ A´‎ A T C O y x P F ‎ 当点P与B重合时，AT=2AB=8，点T的坐标是(2，0)‎ ‎ 又由(1)中求得当A´与B重合时，T的坐标是(6，0)‎ B E ‎ 所以当纸片重叠部分的图形是四边形时，。‎ ‎ (3)S存在最大值 ‎ 当时，，‎ ‎ 在对称轴t=10的左边，S的值随着t的增大而减小，‎ ‎∴当t=6时，S的值最大是。‎ 当时，由图，重叠部分的面积 ‎∵△A´EB的高是，‎ ‎∴‎ ‎ ‎ 当t=2时，S的值最大是；‎ 当，即当点A´和点P都在线段AB的延长线是(如图，其中E是TA´与CB的交点，F是TP与CB的交点)，‎ ‎∵，四边形ETAB是等腰形，∴EF=ET=AB=4，‎ ‎∴‎ 综上所述，S的最大值是，此时t的值是。‎ 图5‎ ‎14、（2011年北京四中中考模拟18） 已知二次函数的图象经过点（2，0）、（－1，6）。 （1）求二次函数的解析式； （2）画出它的图象； （3）写出它的对称轴和顶点坐标。 ‎ 解：（1）依题意，得：，解得：‎ ‎　　所以，二次函数的解析式为：y＝2x2－4x ‎（2）（图略）；（3）对称轴为x＝1，顶点坐标为（1，－2）。‎ ‎15、（2011年北京四中中考模拟19）（本小题满分6分）‎ ‎ 已知抛物线与x轴交于A（－1，0）和B（3，0）两点，且与y轴交于点C（0，3）。‎ ‎（1）求抛物线的解析式；（2）抛物线的对称轴方程和顶点M坐标；（3）求四边形ABMC的面积。‎ 解：（1）y=—x2+2x+3；（2）x=1，M（1，4），（3）9；‎ ‎16、（北京四中模拟）‎ 已知：二次函数的图象与X轴交于A（1，0）、B（5，0），抛物线的顶点为P，且PB=，‎ 求：（1）二次函数的解析式。‎ ‎（2）求出这个二次函数的图象；‎ ‎（3）根据图象回答：当x取什么值时，y的值不小于0。‎ 解（1）由题意，设二次函数的解析式为y=a(x-1)(x-5),即y=ax2-6ax+‎‎5a ‎ 对称轴为x=3，设对称轴与x轴的交点为C(3,0)‎ ‎ ∴OC=3 ∵OB=5 ∴BC=2‎ ‎ ∵P是顶点，BP= ∴PC=4 P（3，-4）‎ ‎ ∴ ∴‎ ‎ ∴二次函数的解析式为 ‎ （2）略 （3）当11‎ ‎∴美丽抛物线的顶点只有B1B2.‎ ‎①若B1为顶点，由B1(1,)，则d=1-=‎ ‎②若B2为顶点，由B2(2,)，则d=1-=‎ 综上所述，d的值为或时，存在美丽抛物线。‎ ‎2. （2011浙江慈吉 模拟）已知如图, 四边形ABCD是平行四边形, A、B均在轴上, 点C的坐标是(6, 3), AD所在的直线的解析式为.‎ ‎ (1)求A、B、D的坐标；‎ ‎(2)以D为顶点的抛物线经过点B, 若将抛物线向上平移()个单位后经过点A, 求原抛物线的解析式及的值.‎ 答案：‎ ‎（1）当时，，得 ‎ 点A的坐标为（） ‎ ‎ 四边形ABCD是平行四边形 ‎ AB∥CD，AB=CD ‎ ‎ ‎ ‎ 得 点D的坐标为（） ‎ ‎ AB=CD=‎ ‎ 点B的坐标是（） ‎ ‎ （2）设原抛物线的解析式为 ‎ 把点B的坐标（）代入得 ‎ ‎ ‎ ‎ 原抛物线的解析式为 ‎ ‎ 设原抛物线向上平移个单位后的解析式为 ‎ 把点A（）代入得 ‎ ‎ ‎ ‎3．（ 2011年杭州三月月考）如图，已知抛物线与轴交于点，，与轴交于点．‎ ‎（1）求抛物线的解析式及其顶点的坐标；‎ ‎（2）设直线交轴于点．在线段的垂直平分线上是否存在点，使得点到直线的距离等于点到原点的距离？如果存在，求出点的坐标；如果不存在，请说明理由；‎ A B C O x y ‎（3）过点作轴的垂线，交直线于点，将抛物线沿其对称轴平移，使抛物线与线段总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？‎ 答案： ‎ ‎（1）设抛物线解析式为，把代入得．‎ ‎，　顶点 ‎ ‎（2）假设满足条件的点存在，依题意设，‎ 由求得直线的解析式为，‎ 它与轴的夹角为，设的中垂线交于，则．‎ 则，点到的距离为．‎ 又． ‎ ‎．‎ 平方并整理得：‎ ‎．‎ 存在满足条件的点，的坐标为． ‎ ‎（3）由上求得．‎ ‎①若抛物线向上平移，可设解析式为．‎ 当时，．‎ 当时，．‎ A B C O x y D F H P E 或．‎ ‎． ‎ ‎②若抛物线向下移，可设解析式为．‎ 由，‎ 有．‎ ‎，．‎ 向上最多可平移72个单位长，向下最多可平移个单位长． ‎ ‎４．（2011年三门峡实验中学3月模拟）如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.‎ ‎（1）求这个二次函数的表达式．‎ ‎（2）连结PO、PC，并把△POC沿CO翻折，得到四边形POＰC， 那么是否存在点P，使四边形POＰC为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．‎ ‎（3）当点P运动到什么位置时，四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.‎ 答案：‎ 解：（1）将B、C两点的坐标代入得 ‎ 解得： ‎ 所以二次函数的表达式为： ． ‎ ‎（2）存在点P，使四边形POPC为菱形．设P点坐标为（x，），‎ PP交CO于E 若四边形POPC是菱形，则有PC＝PO．‎ 连结PP 则PE⊥CO于E，‎ ‎∴OE=EC=‎ ‎∴=．‎ ‎∴= ‎ 解得=，=（不合题意，舍去）‎ ‎∴P点的坐标为（，） ‎ ‎（3）过点P作轴的平行线与BC交于点Q，与OB交于点F，‎ 设P（x，），‎ 易得，直线BC的解析式为 则Q点的坐标为（x，x－3）. ‎ ‎= ‎ 当时，四边形ABPC的面积最大 此时P点的坐标为，四边形ABPC的面积．‎ ‎5.（2011浙江杭州义蓬一模）如图①， 已知抛物线（a≠0）与轴交于点A(1，0)和点B (－3，0)，与y轴交于点C．‎ 图①‎ 图②‎ ‎(1) 求抛物线的解析式；‎ ‎(2) 设抛物线的对称轴与轴交于点N ，问在对称轴上是否存在点P，使△‎ CNP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．‎ ‎(3) 如图②，若点E为第三象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标.‎ 答案：‎ 如图①， 已知抛物线（a≠0）与轴交于点A(1，0)和点B (－3，0)，与y轴交于点C．‎ ‎(1) y=x+2x-3 ‎ ‎(2)P(-1,),P(-1,- ),P(-1,-6),P(-1,-) ‎ ‎(3) S=1/2×3×(-x-2x+3)+ 1/2×3×(-x)‎ S=-3/2(x+3/2)+63/8‎ X=-3/2 , S=63/8 ‎ E(-3/2,-15/4) ‎ ‎6. （2011广东南塘二模）已知抛物线y＝‎ ‎（1）求抛物线与坐标轴的交点坐标；‎ ‎（2）不列表画出大致图象，根据图象求当y＜0时自变量x的取值范围。‎ 答案：（1）(－1，0)、(3，0)、(0，－2)‎ ‎（2）－1＜x＜3‎ ‎7.（浙江杭州金山学校2011模拟）（根据杭州启正中学2010学年第二学期九下期初摸底卷第14题改编）已知关于的函数的图像与坐标轴只有2个交点，求的值.‎ 答案：解：分情况讨论：‎ ‎（ⅰ）时，得. 此时与坐标轴有两个交点，符合题意. ‎ ‎（ⅱ）时，得到一个二次函数.‎ ① 抛物线与x轴只有一个交点， 解得 ‎ ‎ ② 抛物线与x轴有两个交点，其中一个交点是（0,0） ‎ ‎ 把（0,0）带入函数解析式，易得 ‎ y x O A B C ‎8．（2011年海宁市盐官片一模）如图，抛物线经过、两点，与轴交于另一点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）已知点在第一象限的抛物线上，求点关于直线对称的点的坐标；‎ ‎（3）在（2）的条件下，连接，点为抛物线上一点，且，求点的坐标．‎ 答案：解：（1）抛物线经过，两点，‎ ‎ 解得 抛物线的解析式为．‎ y x O A B C D E ‎（2）点在抛物线上，，‎ 即，或．‎ 点在第一象限，点的坐标为．‎ 由（1）知．‎ 设点关于直线的对称点为点．‎ ‎，，且，‎ ‎，‎ y x O A B C D E P F 点在轴上，且．‎ ‎，．‎ 即点关于直线对称的点的坐标为（0，1）．‎ ‎（3）作于，于．‎ 由（1）有：，‎ ‎．‎ ‎，且．‎ ‎，‎ ‎．‎ ‎，，，‎ ‎．‎ 设，则，，‎ ‎．‎ 点在抛物线上，‎ ‎，‎ ‎（舍去）或，．‎ y x O ‎4‎ ‎8‎ ‎－8‎ ‎－4‎ ‎9．（赵州二中九年级七班模拟）已知抛物线y＝(k－1)x2＋2kx＋k－2与x轴有两个不同的交点。‎ ‎(1)求k的取值范围；‎ ‎(2)当k为整数，且关于x的方程3x＝kx－1的解是负数时，求抛物线的解析式；‎ ‎(3)在(2)的条件下，若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形，使得正方形的一边在x轴上，其对边的两个端点在抛物线上，试求出这个最大正方形的边长。‎ 答案：‎ 解：(1)，‎ 依题意，得 ‎ ‎∴的取值范围是且． ① ‎ ‎(2)解方程，得 ‎． ‎ ‎∵方程的解是负数，‎ ‎∴． ∴． ② ‎ 综合①②，及为整数，可得 ．‎ ‎∴抛物线解析式为 ． ‎ ‎(3)如图，设最大正方形ABCD的边长为m，则B、C两点的纵坐标为，‎ 且由对称性可知：B、C两点关于抛物线对称轴对称．‎ ‎∵抛物线的对称轴为：．‎ ‎∴点C的坐标为． ‎ ‎∵C点在抛物线上，‎ ‎∴．‎ 整理，得 ．‎ ‎∴(舍负)‎ ‎∴．‎