海南省中考数学试卷含答案解析

海南省中考数学试卷含答案解析

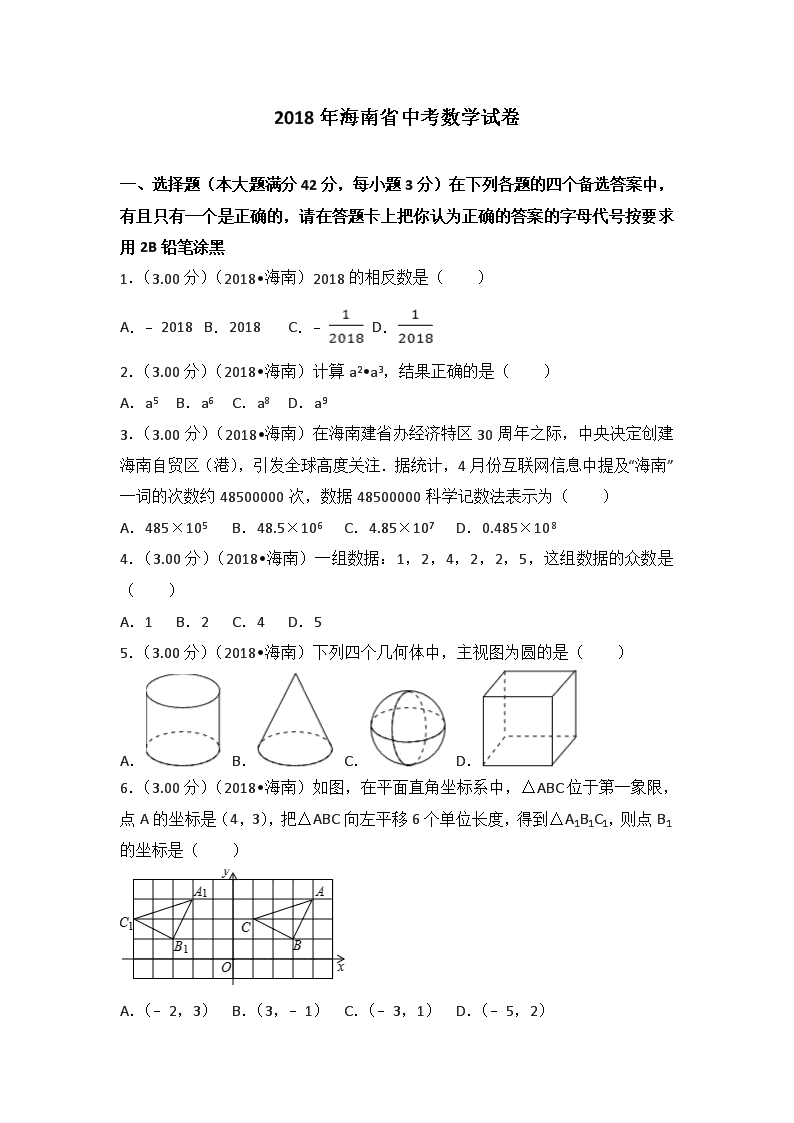
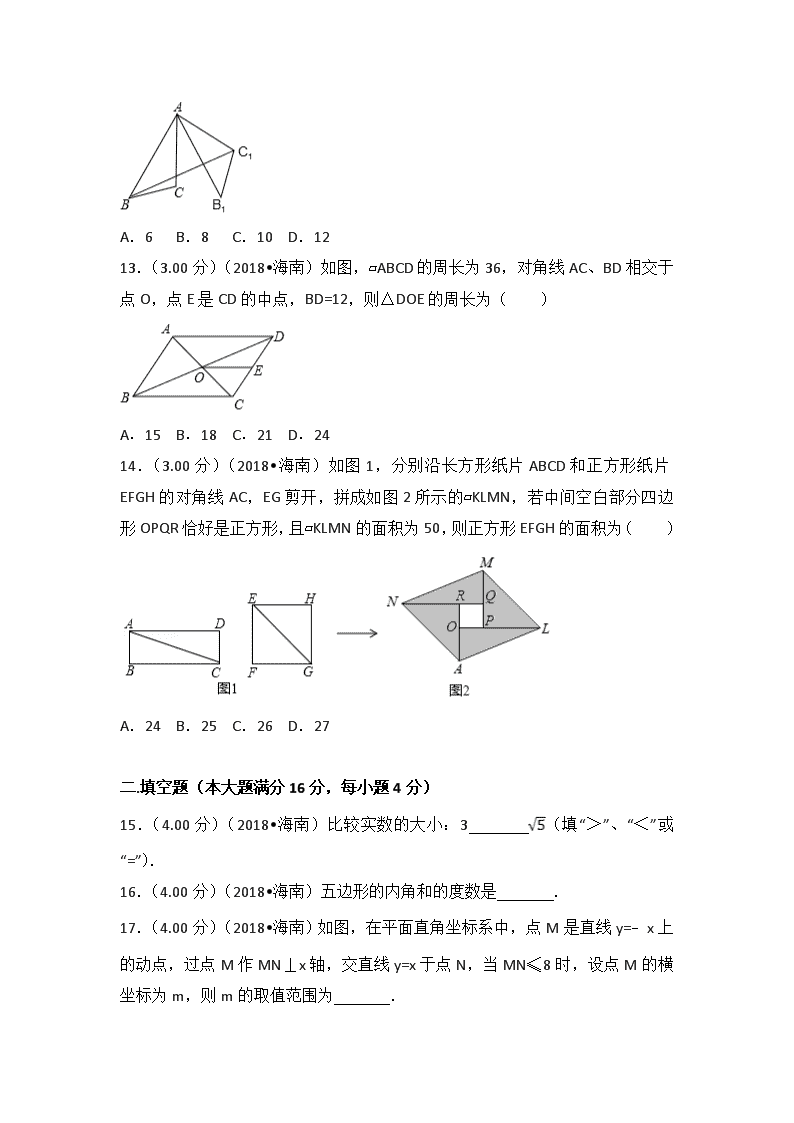
‎2018年海南省中考数学试卷 ‎　‎ 一、选择题（本大题满分42分，每小题3分）在下列各题的四个备选答案中，有且只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑 ‎1．（3.00分）（2018•海南）2018的相反数是（　　）‎ A．﹣2018 B．2018 C．﹣ D． ‎2．（3.00分）（2018•海南）计算a2•a3，结果正确的是（　　）‎ A．a5 B．a6 C．a8 D．a9‎ ‎3．（3.00分）（2018•海南）在海南建省办经济特区30周年之际，中央决定创建海南自贸区（港），引发全球高度关注．据统计，4月份互联网信息中提及“海南”一词的次数约48500000次，数据48500000科学记数法表示为（　　）‎ A．485×105 B．48.5×106 C．4.85×107 D．0.485×108‎ ‎4．（3.00分）（2018•海南）一组数据：1，2，4，2，2，5，这组数据的众数是（　　）‎ A．1 B．2 C．4 D．5‎ ‎5．（3.00分）（2018•海南）下列四个几何体中，主视图为圆的是（　　）‎ A． B． C． D．‎ ‎6．（3.00分）（2018•海南）如图，在平面直角坐标系中，△ABC位于第一象限，点A的坐标是（4，3），把△ABC向左平移6个单位长度，得到△A1B1C1，则点B1的坐标是（　　）‎ A．（﹣2，3） B．（3，﹣1） C．（﹣3，1） D．（﹣5，2）‎ ‎7．（3.00分）（2018•海南）将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE=40°，那么∠BAF的大小为（　　）‎ A．10° B．15° C．20° D．25°‎ ‎8．（3.00分）（2018•海南）下列四个不等式组中，解集在数轴上表示如图所示的是（　　）‎ A． B． C． D． ‎9．（3.00分）（2018•海南）分式方程=0的解是（　　）‎ A．﹣1 B．1 C．±1 D．无解 ‎10．（3.00分）（2018•海南）在一个不透明的袋子中装有n个小球，这些球除颜色外均相同，其中红球有2个，如果从袋子中随机摸出一个球，这个球是红球的概率为，那么n的值是（　　）‎ A．6 B．7 C．8 D．9‎ ‎11．（3.00分）（2018•海南）已知反比例函数y=的图象经过点P（﹣1，2），则这个函数的图象位于（　　）‎ A．二、三象限 B．一、三象限 C．三、四象限 D．二、四象限 ‎12．（3.00分）（2018•海南）如图，在△ABC中，AB=8，AC=6，∠BAC=30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为（　　）‎ A．6 B．8 C．10 D．12‎ ‎13．（3.00分）（2018•海南）如图，▱ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）‎ A．15 B．18 C．21 D．24‎ ‎14．（3.00分）（2018•海南）如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的▱KLMN，若中间空白部分四边形OPQR恰好是正方形，且▱KLMN的面积为50，则正方形EFGH的面积为（　　）‎ A．24 B．25 C．26 D．27‎ ‎　‎ 二.填空题（本大题满分16分，每小题4分）‎ ‎15．（4.00分）（2018•海南）比较实数的大小：3　 　（填“＞”、“＜”或“=”）．‎ ‎16．（4.00分）（2018•海南）五边形的内角和的度数是　 　．‎ ‎17．（4.00分）（2018•海南）如图，在平面直角坐标系中，点M是直线y=﹣x上的动点，过点M作MN⊥x轴，交直线y=x于点N，当MN≤8时，设点M的横坐标为m，则m的取值范围为　 　．‎ ‎18．（4.00分）（2018•海南）如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为　 　．‎ ‎　‎ 三、解答题（本大题满分62分）‎ ‎19．（10.00分）（2018•海南）计算：‎ ‎（1）32﹣﹣|﹣2|×2﹣1‎ ‎（2）（a+1）2+2（1﹣a）‎ ‎20．（8.00分）（2018•海南）“绿水青山就是金山银山”，海南省委省政府高度重视环境生态保护，截至2017年底，全省建立国家级、省级和市县级自然保护区共49个，其中国家级10个，省级比市县级多5个．问省级和市县级自然保护区各多少个？‎ ‎21．（8.00分）（2018•海南）海南建省30年来，各项事业取得令人瞩目的成就，以2016年为例，全省社会固定资产总投资约3730亿元，其中包括中央项目、省属项目、地（市）属项目、县（市）属项目和其他项目．图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图，请完成下列问题：‎ ‎（1）在图1中，先计算地（市）属项目投资额为　 　亿元，然后将条形统计图补充完整；‎ ‎（2）在图2中，县（市）属项目部分所占百分比为m%、对应的圆心角为β，则m=　 　，β=　 　度（m、β均取整数）．‎ ‎22．（8.00分）（2018•海南）如图，某数学兴趣小组为测量一棵古树BH和教学楼CG的高，先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°，此时教学楼顶端G恰好在视线DH上，再向前走7米到达B处，又测得教学楼顶端G的仰角∠GEF为60°，点A、B、C三点在同一水平线上．‎ ‎（1）计算古树BH的高；‎ ‎（2）计算教学楼CG的高．（参考数据：≈14，≈1.7）‎ ‎23．（13.00分）（2018•海南）已知，如图1，在▱ABCD中，点E是AB中点，连接DE并延长，交CB的延长线于点F．‎ ‎（1）求证：△ADE≌△BFE；‎ ‎（2）如图2，点G是边BC上任意一点（点G不与点B、C重合），连接AG交DF于点H，连接HC，过点A作AK∥HC，交DF于点K．‎ ‎①求证：HC=2AK；‎ ‎②当点G是边BC中点时，恰有HD=n•HK（n为正整数），求n的值．‎ ‎24．（15.00分）（2018•海南）如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．‎ ‎（1）求该抛物线所对应的函数解析式；‎ ‎（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．‎ ‎①求四边形ACFD的面积；‎ ‎②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q的坐标．‎ ‎　‎ ‎2018年海南省中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题满分42分，每小题3分）在下列各题的四个备选答案中，有且只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑 ‎1．（3.00分）（2018•海南）2018的相反数是（　　）‎ A．﹣2018 B．2018 C．﹣ D． ‎【考点】14：相反数．‎ ‎【专题】1 ：常规题型．‎ ‎【分析】直接利用相反数的定义分析得出答案．‎ ‎【解答】解：2018的相反数是：﹣2018．‎ 故选：A．‎ ‎【点评】此题主要考查了相反数，正确把握相反数的定义是解题关键．‎ ‎　‎ ‎2．（3.00分）（2018•海南）计算a2•a3，结果正确的是（　　）‎ A．a5 B．a6 C．a8 D．a9‎ ‎【考点】46：同底数幂的乘法．‎ ‎【专题】11 ：计算题．‎ ‎【分析】根据同底数幂的乘法法则解答即可．‎ ‎【解答】解：a2•a3=a5，‎ 故选：A．‎ ‎【点评】此题考查同底数幂的乘法，关键是根据同底数的幂的乘法解答．‎ ‎　‎ ‎3．（3.00分）（2018•海南）在海南建省办经济特区30周年之际，中央决定创建海南自贸区（港），引发全球高度关注．据统计，4月份互联网信息中提及“海南”一词的次数约48500000次，数据48500000科学记数法表示为（　　）‎ A．485×105 B．48.5×106 C．4.85×107 D．0.485×108‎ ‎【考点】1I：科学记数法—表示较大的数．‎ ‎【专题】1 ：常规题型．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：48500000用科学记数法表示为4.85×107，‎ 故选：C．‎ ‎【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎4．（3.00分）（2018•海南）一组数据：1，2，4，2，2，5，这组数据的众数是（　　）‎ A．1 B．2 C．4 D．5‎ ‎【考点】W5：众数．‎ ‎【专题】1 ：常规题型．‎ ‎【分析】根据众数定义可得答案．‎ ‎【解答】解：一组数据：1，2，4，2，2，5，这组数据的众数是2，‎ 故选：B．‎ ‎【点评】此题主要考查了众数，关键是掌握一组数据中出现次数最多的数据叫做众数．‎ ‎　‎ ‎5．（3.00分）（2018•海南）下列四个几何体中，主视图为圆的是（　　）‎ A． B． C． D．‎ ‎【考点】U1：简单几何体的三视图．‎ ‎【分析】先分析出四种几何体的主视图的形状，即可得出主视图为圆的几何体．‎ ‎【解答】解：A、圆柱的主视图是长方形，故A错误；‎ B、圆锥的主视图是三角形，故B错误；‎ C、球的主视图是圆，故C正确；‎ D、正方体的主视图是正方形，故D错误．‎ 故选：C．‎ ‎【点评】本题考查了利用几何体判断三视图，培养了学生的观察能力和对几何体三种视图的空间想象能力．‎ ‎　‎ ‎6．（3.00分）（2018•海南）如图，在平面直角坐标系中，△ABC位于第一象限，点A的坐标是（4，3），把△ABC向左平移6个单位长度，得到△A1B1C1，则点B1的坐标是（　　）‎ A．（﹣2，3） B．（3，﹣1） C．（﹣3，1） D．（﹣5，2）‎ ‎【考点】Q3：坐标与图形变化﹣平移．‎ ‎【专题】1 ：常规题型；558：平移、旋转与对称．‎ ‎【分析】根据点的平移的规律：向左平移a个单位，坐标P（x，y）⇒P（x﹣a，y），据此求解可得．‎ ‎【解答】解：∵点B的坐标为（3，1），‎ ‎∴向左平移6个单位后，点B1的坐标（﹣3，1），‎ 故选：C．‎ ‎【点评】本题主要考查坐标与图形的变化﹣平移，解题的关键是掌握点的坐标的平移规律：横坐标，右移加，左移减；纵坐标，上移加，下移减．‎ ‎　‎ ‎7．（3.00分）（2018•海南）将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE=40°，那么∠BAF的大小为（　　）‎ A．10° B．15° C．20° D．25°‎ ‎【考点】JA：平行线的性质．‎ ‎【专题】1 ：常规题型；551：线段、角、相交线与平行线．‎ ‎【分析】由DE∥AF得∠AFD=∠CDE=40°，再根据三角形的外角性质可得答案．‎ ‎【解答】解：由题意知DE∥AF，‎ ‎∴∠AFD=∠CDE=40°，‎ ‎∵∠B=30°，‎ ‎∴∠BAF=∠AFD﹣∠B=40°﹣30°=10°，‎ 故选：A．‎ ‎【点评】本题主要考查平行线的性质，解题的关键是掌握两直线平行同位角相等与三角形外角的性质．‎ ‎　‎ ‎8．（3.00分）（2018•海南）下列四个不等式组中，解集在数轴上表示如图所示的是（　　）‎ A． B． C． D． ‎【考点】C4：在数轴上表示不等式的解集．‎ ‎【专题】1 ：常规题型；524：一元一次不等式(组)及应用．‎ ‎【分析】根据不等式组的表示方法，可得答案．‎ ‎【解答】解：由解集在数轴上的表示可知，该不等式组为，‎ 故选：D．‎ ‎【点评】‎ 本题考查了在数轴上表示不等式的解集，利用不等式组的解集的表示方法：大小小大中间找是解题关键．‎ ‎　‎ ‎9．（3.00分）（2018•海南）分式方程=0的解是（　　）‎ A．﹣1 B．1 C．±1 D．无解 ‎【考点】B2：分式方程的解．‎ ‎【专题】11 ：计算题；522：分式方程及应用．‎ ‎【分析】根据解分式方程的步骤计算可得．‎ ‎【解答】解：两边都乘以x+1，得：x2﹣1=0，‎ 解得：x=1或x=﹣1，‎ 当x=1时，x+1≠0，是方程的解；‎ 当x=﹣1时，x+1=0，是方程的增根，舍去；‎ 所以原分式方程的解为x=1，‎ 故选：B．‎ ‎【点评】本题主要考查分式方程的解，解题的关键是熟练掌握解分式方程的步骤．‎ ‎　‎ ‎10．（3.00分）（2018•海南）在一个不透明的袋子中装有n个小球，这些球除颜色外均相同，其中红球有2个，如果从袋子中随机摸出一个球，这个球是红球的概率为，那么n的值是（　　）‎ A．6 B．7 C．8 D．9‎ ‎【考点】X4：概率公式．‎ ‎【专题】1 ：常规题型．‎ ‎【分析】根据概率公式得到=，然后利用比例性质求出n即可．‎ ‎【解答】解：根据题意得=，解得n=6，‎ 所以口袋中小球共有6个．‎ 故选：A．‎ ‎【点评】本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．‎ ‎　‎ ‎11．（3.00分）（2018•海南）已知反比例函数y=的图象经过点P（﹣1，2），则这个函数的图象位于（　　）‎ A．二、三象限 B．一、三象限 C．三、四象限 D．二、四象限 ‎【考点】G6：反比例函数图象上点的坐标特征．‎ ‎【分析】先根据点P的坐标求出反比例函数的比例系数k，再由反比例函数的性质即可得出结果．‎ ‎【解答】解：反比例函数y=的图象经过点P（﹣1，2），‎ ‎∴2=．‎ ‎∴k=﹣2＜0；‎ ‎∴函数的图象位于第二、四象限．‎ 故选：D．‎ ‎【点评】本题考查了反比例函数的图象和性质：①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．‎ ‎　‎ ‎12．（3.00分）（2018•海南）如图，在△ABC中，AB=8，AC=6，∠BAC=30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为（　　）‎ A．6 B．8 C．10 D．12‎ ‎【考点】KQ：勾股定理；R2：旋转的性质；T7：解直角三角形．‎ ‎【专题】55：几何图形．‎ ‎【分析】根据旋转的性质得出AC=AC1，∠BAC1=90°，进而利用勾股定理解答即可．‎ ‎【解答】解：∵将△ABC绕点A逆时针旋转60°得到△AB1C1，‎ ‎∴AC=AC1，∠CAC1=90°，‎ ‎∵AB=8，AC=6，∠BAC=30°，‎ ‎∴∠BAC1=90°，AB=8，AC1=6，‎ ‎∴在Rt△BAC1中，BC1的长=，‎ 故选：C．‎ ‎【点评】此题考查旋转的性质，关键是根据旋转的性质得出AC=AC1，∠BAC1=90°．‎ ‎　‎ ‎13．（3.00分）（2018•海南）如图，▱ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）‎ A．15 B．18 C．21 D．24‎ ‎【考点】KX：三角形中位线定理；L5：平行四边形的性质．‎ ‎【专题】555：多边形与平行四边形．‎ ‎【分析】利用平行四边形的性质，三角形中位线定理即可解决问题；‎ ‎【解答】解：∵平行四边形ABCD的周长为36，‎ ‎∴BC+CD=18，‎ ‎∵OD=OB，DE=EC，‎ ‎∴OE+DE=（BC+CD）=9，‎ ‎∵BD=12，‎ ‎∴OD=BD=6，‎ ‎∴△DOE的周长为9+6=15，‎ 故选：A．‎ ‎【点评】本题考查平行四边形的性质、三角形的中位线定理等知识，解题的关键是熟练掌握三角形中位线定理，属于中考常考题型．‎ ‎　‎ ‎14．（3.00分）（2018•海南）如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的▱KLMN，若中间空白部分四边形OPQR恰好是正方形，且▱KLMN的面积为50，则正方形EFGH的面积为（　　）‎ A．24 B．25 C．26 D．27‎ ‎【考点】L7：平行四边形的判定与性质；LB：矩形的性质；LE：正方形的性质；PC：图形的剪拼．‎ ‎【专题】556：矩形 菱形 正方形．‎ ‎【分析】如图，设PM=PL=NR=AR=a，正方形ORQP的边长为b，构建方程即可解决问题；‎ ‎【解答】解：如图，设PM=PL=NR=AR=a，正方形ORQP的边长为b．‎ 由题意：a2+b2+（a+b）（a﹣b）=50，‎ ‎∴a2=25，‎ ‎∴正方形EFGH的面积=a2=25，‎ 故选：B．‎ ‎【点评】本题考查图形的拼剪，矩形的性质，正方形的性质等知识，解题的关键是学会利用参数构建方程解决问题，学会利用数形结合的思想解决问题，属于中考选择题中的压轴题．‎ ‎　‎ 二.填空题（本大题满分16分，每小题4分）‎ ‎15．（4.00分）（2018•海南）比较实数的大小：3　＞　（填“＞”、“＜”或“=”）．‎ ‎【考点】2A：实数大小比较．‎ ‎【专题】11 ：计算题．‎ ‎【分析】根据3=＞计算．‎ ‎【解答】解：∵3=，＞，‎ ‎∴3＞．‎ 故答案是：＞．‎ ‎【点评】本题考查了实数的大小比较的应用，主要考查了学生的比较能力．‎ ‎　‎ ‎16．（4.00分）（2018•海南）五边形的内角和的度数是　540°　．‎ ‎【考点】L3：多边形内角与外角．‎ ‎【分析】根据n边形的内角和公式：180°（n﹣2），将n=5代入即可求得答案．‎ ‎【解答】解：五边形的内角和的度数为：180°×（5﹣2）=180°×3=540°．‎ 故答案为：540°．‎ ‎【点评】此题考查了多边形的内角和公式．此题比较简单，准确记住公式是解此题的关键．‎ ‎　‎ ‎17．（4.00分）（2018•海南）如图，在平面直角坐标系中，点M是直线y=﹣x上的动点，过点M作MN⊥x轴，交直线y=x于点N，当MN≤8时，设点M的横坐标为m，则m的取值范围为　﹣4≤m≤4　．‎ ‎【考点】F8：一次函数图象上点的坐标特征．‎ ‎【专题】11 ：计算题．‎ ‎【分析】先确定出M，N的坐标，进而得出MN=|2m|，即可建立不等式，解不等式即可得出结论．‎ ‎【解答】解：∵点M在直线y=﹣x上，‎ ‎∴M（m，﹣m），‎ ‎∵MN⊥x轴，且点N在直线y=x上，‎ ‎∴N（m，m），‎ ‎∴MN=|﹣m﹣m|=|2m|，‎ ‎∵MN≤8，‎ ‎∴|2m|≤8，‎ ‎∴﹣4≤m≤4，‎ 故答案为：﹣4≤m≤4．‎ ‎【点评】此题主要考查了一次函数图象上点的坐标特征，解不等式，表示出MN是解本题的关键．‎ ‎　‎ ‎18．（4.00分）（2018•海南）如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为　（2，6）　．‎ ‎【考点】KQ：勾股定理；L5：平行四边形的性质；M2：垂径定理．‎ ‎【专题】1 ：常规题型．‎ ‎【分析】过点M作MF⊥CD于点F，则CF=CD=8，过点C作CE⊥OA于点E，由勾股定理可求得MF的长，从而得出OE的长，然后写出点C的坐标．‎ ‎【解答】解：∵四边形OCDB是平行四边形，B（16，0），‎ ‎∴CD∥OA，CD=OB=16，‎ 过点M作MF⊥CD于点F，则CF=CD=8，‎ 过点C作CE⊥OA于点E，‎ ‎∵A（20，0），‎ ‎∴OE=OM﹣ME=OM﹣CF=10﹣8=2．‎ 连接MC，则MC=OA=10，‎ ‎∴在Rt△CMF中，由勾股定理得MF==6‎ ‎∴点C的坐标为（2，6）‎ 故答案为：（2，6）．‎ ‎【点评】本题考查了勾股定理、垂径定理以及平行四边形的性质，正确作出辅助线构造出直角三角形是解题关键．‎ ‎　‎ 三、解答题（本大题满分62分）‎ ‎19．（10.00分）（2018•海南）计算：‎ ‎（1）32﹣﹣|﹣2|×2﹣1‎ ‎（2）（a+1）2+2（1﹣a）‎ ‎【考点】2C：实数的运算；36：去括号与添括号；4C：完全平方公式；6F：负整数指数幂．‎ ‎【专题】1 ：常规题型．‎ ‎【分析】（1）直接利用二次根式性质和负指数幂的性质分别化简得出答案；‎ ‎（2）直接利用完全平方公式去括号进而合并同类项得出答案．‎ ‎【解答】解：（1）原式=9﹣3﹣2× ‎=5；‎ ‎（2）原式=a2+2a+1+2﹣2a ‎=a2+3．‎ ‎【点评】此题主要考查了实数运算，正确化简各数是解题关键．‎ ‎　‎ ‎20．（8.00分）（2018•海南）“绿水青山就是金山银山”，海南省委省政府高度重视环境生态保护，截至2017年底，全省建立国家级、省级和市县级自然保护区共49个，其中国家级10个，省级比市县级多5个．问省级和市县级自然保护区各多少个？‎ ‎【考点】8A：一元一次方程的应用．‎ ‎【专题】34 ：方程思想；521：一次方程（组）及应用．‎ ‎【分析】设市县级自然保护区有x个，则省级自然保护区有（x+5）个，根据国家级、省级和市县级自然保护区共49个，即可得出关于x的一元一次方程，解之即可得出结论．‎ ‎【解答】解：设市县级自然保护区有x个，则省级自然保护区有（x+5）个，‎ 根据题意得：10+x+5+x=49，‎ 解得：x=17，‎ ‎∴x+5=22．‎ 答：省级自然保护区有22个，市县级自然保护区有17个．‎ ‎【点评】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．‎ ‎　‎ ‎21．（8.00分）（2018•海南）海南建省30年来，各项事业取得令人瞩目的成就，以2016年为例，全省社会固定资产总投资约3730亿元，其中包括中央项目、省属项目、地（市）属项目、县（市）属项目和其他项目．图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图，请完成下列问题：‎ ‎（1）在图1中，先计算地（市）属项目投资额为　830　亿元，然后将条形统计图补充完整；‎ ‎（2）在图2中，县（市）属项目部分所占百分比为m%、对应的圆心角为β，则m=　18　，β=　65　度（m、β均取整数）．‎ ‎【考点】VB：扇形统计图；VC：条形统计图．‎ ‎【专题】1 ：常规题型；542：统计的应用．‎ ‎【分析】（1）用全省社会固定资产总投资约3730亿元减去其他项目的投资即可求得地（市）属项目投资额，从而补全图象；‎ ‎（2）用县（市）属项目投资除以总投资求得m的值，再用360度乘以县（市）属项目投资额所占比例可得．‎ ‎【解答】解：（1）地（市）属项目投资额为3730﹣（200+530+670+‎ ‎1500）=830（亿元），‎ 补全图形如下：‎ 故答案为：830；‎ ‎（2）（市）属项目部分所占百分比为m%=×100%≈18%，即m=18，‎ 对应的圆心角为β=360°×≈65°，‎ 故答案为：18、65．‎ ‎【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎　‎ ‎22．（8.00分）（2018•海南）如图，某数学兴趣小组为测量一棵古树BH和教学楼CG的高，先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°，此时教学楼顶端G恰好在视线DH上，再向前走7米到达B处，又测得教学楼顶端G的仰角∠GEF为60°，点A、B、C三点在同一水平线上．‎ ‎（1）计算古树BH的高；‎ ‎（2）计算教学楼CG的高．（参考数据：≈14，≈1.7）‎ ‎【考点】TA：解直角三角形的应用﹣仰角俯角问题．‎ ‎【专题】552：三角形．‎ ‎【分析】（1）利用等腰直角三角形的性质即可解决问题；‎ ‎（2）作HJ⊥CG于G．则△HJG是等腰三角形，四边形BCJH是矩形，设HJ=GJ=BC=x．构建方程即可解决问题；‎ ‎【解答】解：（1）由题意：四边形ABED是矩形，可得DE=AB=7米．‎ 在Rt△DEH中，∵∠EDH=45°，‎ ‎∴HE=DE=7米．‎ ‎（2）作HJ⊥CG于G．则△HJG是等腰三角形，四边形BCJH是矩形，设HJ=GJ=BC=x．‎ 在Rt△BCG中，tan60°=，‎ ‎∴=，‎ ‎∴x=+．‎ ‎∴CG=CF+FG=×1.7+3.5+1.5=11.3米．‎ ‎【点评】‎ 本题考查解直角三角形的应用﹣仰角俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．‎ ‎　‎ ‎23．（13.00分）（2018•海南）已知，如图1，在▱ABCD中，点E是AB中点，连接DE并延长，交CB的延长线于点F．‎ ‎（1）求证：△ADE≌△BFE；‎ ‎（2）如图2，点G是边BC上任意一点（点G不与点B、C重合），连接AG交DF于点H，连接HC，过点A作AK∥HC，交DF于点K．‎ ‎①求证：HC=2AK；‎ ‎②当点G是边BC中点时，恰有HD=n•HK（n为正整数），求n的值．‎ ‎【考点】LO：四边形综合题．‎ ‎【专题】152：几何综合题．‎ ‎【分析】（1）根据平行四边形的性质得到AD∥BC，得到∠ADE=∠BFE，∠A=∠FBE，利用AAS定理证明即可；‎ ‎（2）作BN∥HC交EF于N，根据全等三角形的性质、三角形中位线定理证明；‎ ‎（3）作GM∥DF交HC于M，分别证明△CMG∽△CHF、△AHD∽△GHF、△AHK∽△HGM，根据相似三角形的性质计算即可．‎ ‎【解答】（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，‎ ‎∴∠ADE=∠BFE，∠A=∠FBE，‎ 在△ADE和△BFE中，‎ ，‎ ‎∴△ADE≌△BFE；‎ ‎（2）如图2，作BN∥HC交EF于N，‎ ‎∵△ADE≌△BFE，‎ ‎∴BF=AD=BC，‎ ‎∴BN=HC，‎ 由（1）的方法可知，△AEK≌△BFN，‎ ‎∴AK=BN，‎ ‎∴HC=2AK；‎ ‎（3）如图3，作GM∥DF交HC于M，‎ ‎∵点G是边BC中点，‎ ‎∴CG=CF，‎ ‎∵GM∥DF，‎ ‎∴△CMG∽△CHF，‎ ‎∴==，‎ ‎∵AD∥FC，‎ ‎∴△AHD∽△GHF，‎ ‎∴===，‎ ‎∴=，‎ ‎∵AK∥HC，GM∥DF，‎ ‎∴△AHK∽△HGM，‎ ‎∴==，‎ ‎∴=，即HD=4HK，‎ ‎∴n=4．‎ ‎【点评】本题考查的是平行四边形的性质、全等三角形的判定和性质、相似三角形的判定和性质，掌握它们的判定定理和性质定理是解题的关键．‎ ‎　‎ ‎24．（15.00分）（2018•海南）如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．‎ ‎（1）求该抛物线所对应的函数解析式；‎ ‎（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．‎ ‎①求四边形ACFD的面积；‎ ‎②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q的坐标．‎ ‎【考点】HF：二次函数综合题．‎ ‎【专题】16 ：压轴题；32 ：分类讨论；41 ：待定系数法；523：一元二次方程及应用；537：函数的综合应用；554：等腰三角形与直角三角形．‎ ‎【分析】（1）由A、B两点的坐标，利用待定系数法即可求得抛物线解析式；‎ ‎（2）①连接CD，则可知CD∥x轴，由A、F的坐标可知F、A到CD的距离，利用三角形面积公式可求得△ACD和△FCD的面积，则可求得四边形ACFD的面积；②由题意可知点A处不可能是直角，则有∠ADQ=90°或∠AQD=90°，当∠ADQ=90°时，可先求得直线AD解析式，则可求出直线DQ解析式，联立直线DQ和抛物线解析式则可求得Q点坐标；当∠AQD=90°时，设Q（t，﹣t2+2t+3），设直线AQ的解析式为y=k1x+b1，则可用t表示出k′，设直线DQ解析式为y=k2x+b2，同理可表示出k2，由AQ⊥DQ则可得到关于t的方程，可求得t的值，即可求得Q点坐标．‎ ‎【解答】解：‎ ‎（1）由题意可得，解得，‎ ‎∴抛物线解析式为y=﹣x2+2x+3；‎ ‎（2）①∵y=﹣x2+2x+3=﹣（x﹣1）2+4，‎ ‎∴F（1，4），‎ ‎∵C（0，3），D（2，3），‎ ‎∴CD=2，且CD∥x轴，‎ ‎∵A（﹣1，0），‎ ‎∴S四边形ACFD=S△ACD+S△FCD=×2×3+×2×（4﹣3）=4；‎ ‎②∵点P在线段AB上，‎ ‎∴∠DAQ不可能为直角，‎ ‎∴当△AQD为直角三角形时，有∠ADQ=90°或∠AQD=90°，‎ i．当∠ADQ=90°时，则DQ⊥AD，‎ ‎∵A（﹣1，0），D（2，3），‎ ‎∴直线AD解析式为y=x+1，‎ ‎∴可设直线DQ解析式为y=﹣x+b′，‎ 把D（2，3）代入可求得b′=5，‎ ‎∴直线DQ解析式为y=﹣x+5，‎ 联立直线DQ和抛物线解析式可得，解得或，‎ ‎∴Q（1，4）；‎ ii．当∠AQD=90°时，设Q（t，﹣t2+2t+3），‎ 设直线AQ的解析式为y=k1x+b1，‎ 把A、Q坐标代入可得，解得k1=﹣（t﹣3），‎ 设直线DQ解析式为y=k2x+b2，同理可求得k2=﹣t，‎ ‎∵AQ⊥DQ，‎ ‎∴k1k2=﹣1，即t（t﹣3）=﹣1，解得t=，‎ 当t=时，﹣t2+2t+3=，‎ 当t=时，﹣t2+2t+3=，‎ ‎∴Q点坐标为（，）或（，）；‎ 综上可知Q点坐标为（1，4）或（，）或（，）．‎ ‎【点评】本题为二次函数的综合应用，涉及待定系数法、三角形的面积、二次函数的性质、直角三角形的性质及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）①中注意把四边形转化为两个三角形，在②利用互相垂直直线的性质是解题的关键．本题考查知识点较多，综合性较强，难度适中．‎ ‎　‎