- 2021-05-10 发布 |
- 37.5 KB |
- 4页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题练习7 四边形
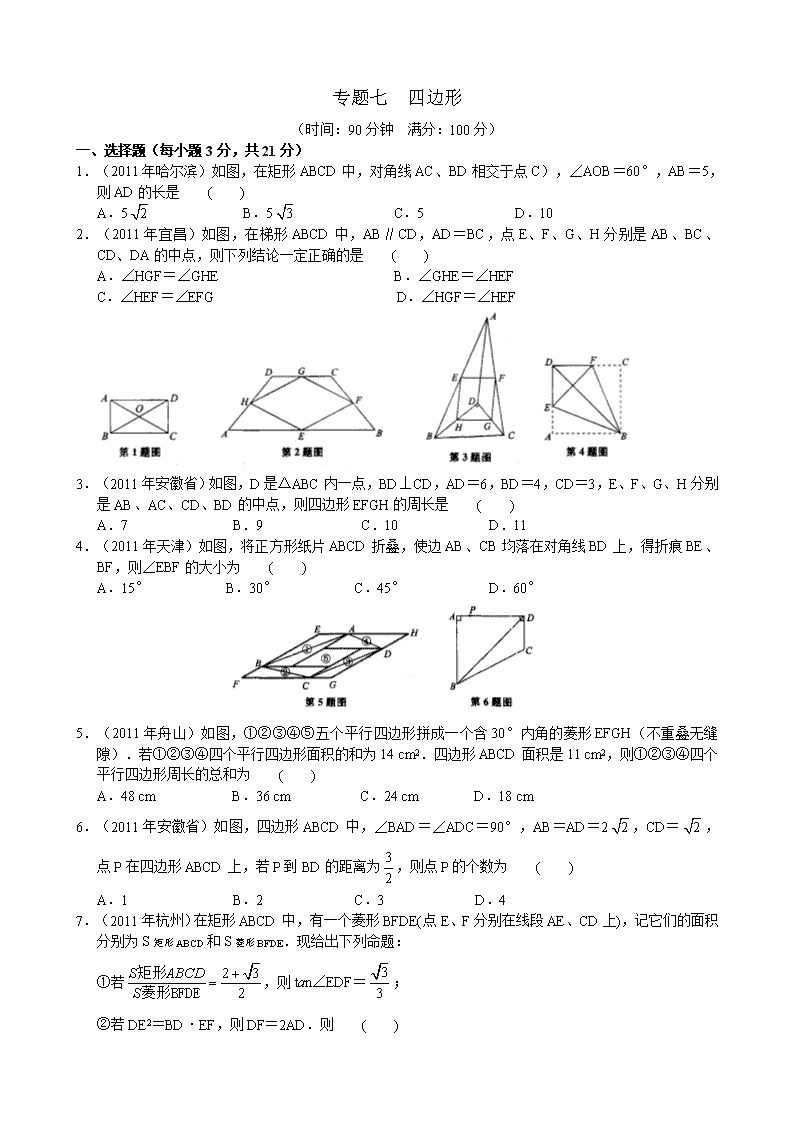
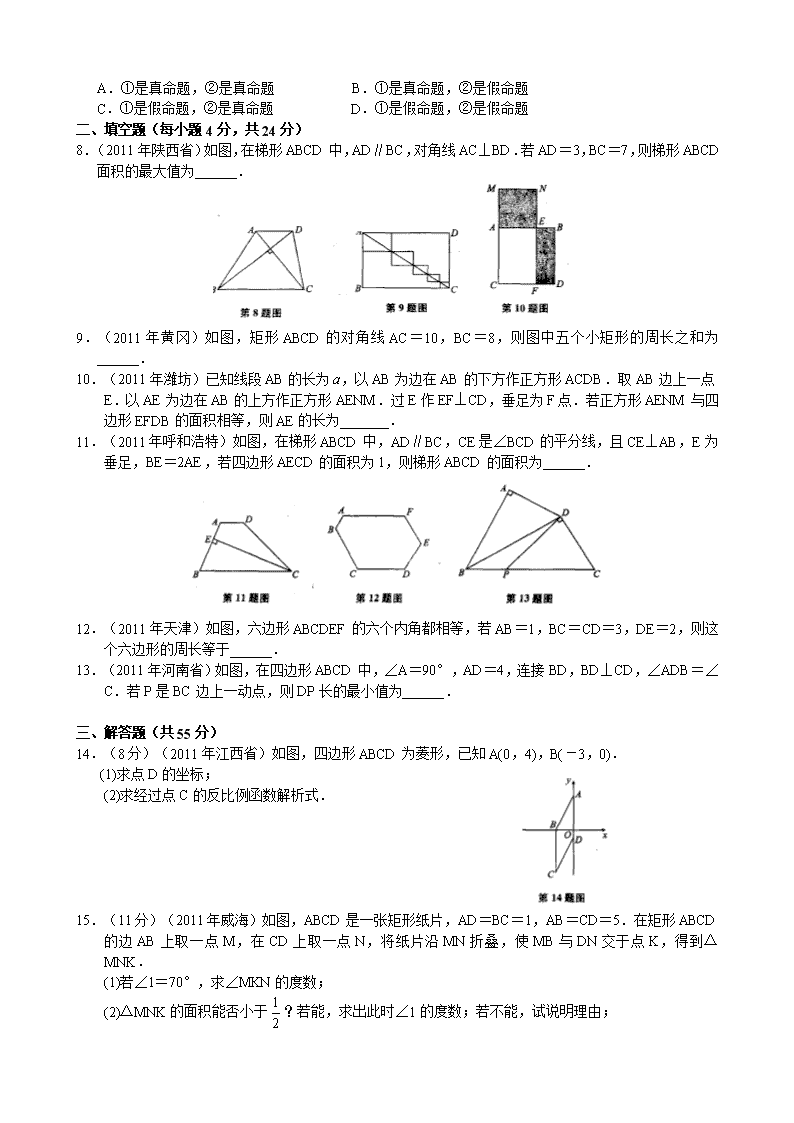
专题七 四边形 (时间:90分钟 满分:100分) 一、选择题(每小题3分,共21分) 1.(2011年哈尔滨)如图,在矩形ABCD中,对角线AC、BD相交于点C),∠AOB=60°,AB=5,则AD的长是 ( ) A.5 B.5 C.5 D.10 2.(2011年宜昌)如图,在梯形ABCD中,AB∥CD,AD=BC,点E、F、G、H分别是AB、BC、CD、DA的中点,则下列结论一定正确的是 ( ) A.∠HGF=∠GHE B.∠GHE=∠HEF C.∠HEF=∠EFG D.∠HGF=∠HEF 3.(2011年安徽省)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 ( ) A.7 B.9 C.10 D.11 4.(2011年天津)如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为 ( ) A.15° B.30° C.45° D.60° 5.(2011年舟山)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14 cm2.四边形ABCD面积是11 cm2,则①②③④四个平行四边形周长的总和为 ( ) A.48 cm B.36 cm C.24 cm D.18 cm 6.(2011年安徽省)如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2,CD=,点P在四边形ABCD上,若P到BD的距离为,则点P的个数为 ( ) A.1 B.2 C.3 D.4 7.(2011年杭州)在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AE、CD上),记它们的面积分别为S矩形ABCD和S菱形BFDE.现给出下列命题: ①若,则tan∠EDF=; ②若DE2=BD·EF,则DF=2AD.则 ( ) A.①是真命题,②是真命题 B.①是真命题,②是假命题 C.①是假命题,②是真命题 D.①是假命题,②是假命题 二、填空题(每小题4分,共24分) 8.(2011年陕西省)如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD.若AD=3,BC=7,则梯形ABCD面积的最大值为______. 9.(2011年黄冈)如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为______. 10.(2011年潍坊)已知线段AB的长为a,以AB为边在AB的下方作正方形ACDB.取AB边上一点E.以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,则AE的长为_______. 11.(2011年呼和浩特)如图,在梯形ABCD中,AD∥BC,CE是∠BCD的平分线,且CE⊥AB,E为垂足,BE=2AE,若四边形AECD的面积为1,则梯形ABCD的面积为______. 12.(2011年天津)如图,六边形ABCDEF的六个内角都相等,若AB=1,BC=CD=3,DE=2,则这个六边形的周长等于______. 13.(2011年河南省)如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为______. 三、解答题(共55分) 14.(8分)(2011年江西省)如图,四边形ABCD为菱形,已知A(0,4),B(-3,0). (1)求点D的坐标; (2)求经过点C的反比例函数解析式. 15.(11分)(2011年威海)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK. (1)若∠1=70°,求∠MKN的度数; (2)△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由; (3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值. 16.(12分)(2011年杭州)在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于O,线段OA、OB的中点分别为点E、F. (1)求证:△FOE≌△DOC; (2)求sin∠OEF的值; (3)若直线EF与线段AD、BC分别相交于点G、H,求的值. 17.(12分)(2011年北京)在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F. (1)在图(1)中证明CE=CF; (2)若∠ABC=90°,G是EF的中点(如图(2)),直接写出∠BDG的度数; (3)若∠ABC=120°,FGQ∥CE,FG=CE,分别连接DB、DG(如图(3)),求∠BDG的度数. 18.(12分)(2011年哈尔滨)如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD为菱形,AB边在x轴上,点D在y轴上,点A的坐标是(-6,0),AB=10. (1)求点C的坐标; (2)连接BD,点P是线段CD上一动点(点P不与C、D两点重合),过点P作PE∥BC交BD于点E,过点B作BQ⊥PE交PE的延长线于点Q.设PC的长为x,PQ的长为y,求y与x之间的函数关系式(直接写出自变量x的取值范围); (3)在(2)的条件下,连接AQ、AE,当x为何值时,S△BQE+S△AQE=S△DEP?并判断此时以点P为圆心,以5为半径的⊙P与直线BC的位置关系,请说明理由. 参考答案 1.B 2.D 3.D 4.C 5.A 6.B 7.A 8. 25 9. 28 10. 11. 12. 15 13.4 14.(1)(0,-1) (2) 15.(1)40° (2)不能 (3)分两种情况:情况一:如图(2),将矩形纸片对折,使点B与点D重合,此时点K也与点D重合. 情况二:如图(3),将矩形纸片沿对角线AC对折,此时折痕即为AC. △MNK面积的最大值为1.3 16.(1)略 (2) (3) 17.(1)略 (2)45° (3)60° 18.(1)(10,8) (2) (3)x=5 ⊙P与直线BC相交查看更多