- 2021-05-10 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题二次函数的图象和性质
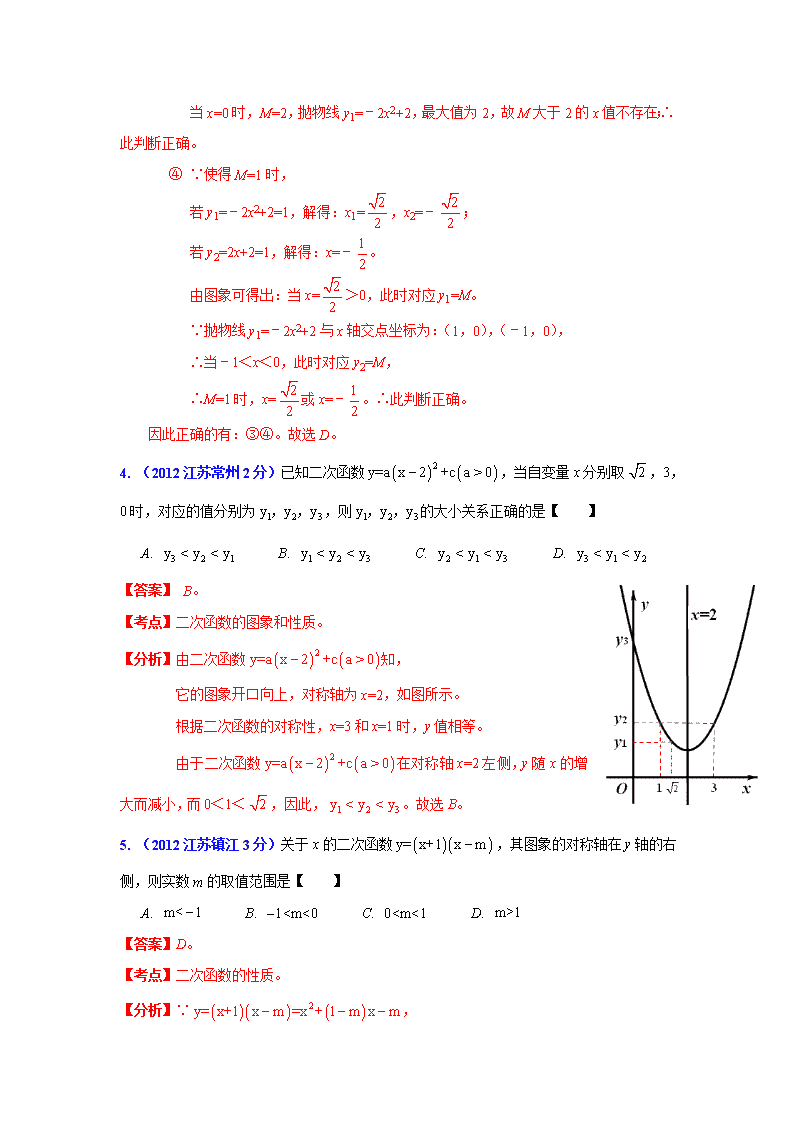
2012年全国中考数学试题分类解析汇编(159套63专题) 专题21:二次函数的图象和性质 一、选择题 1. (2012重庆市4分)已知二次函数的图象如图所示对称轴为。下列结论中,正确的是【 】 A. B. C. D. 【答案】D。 【考点】二次函数图象与系数的关系。 【分析】A、∵二次函数的图象开口向上,∴>0。 ∵二次函数的图象与轴交于负半轴,∴<0。 ∵二次函数的图象对称轴在轴左侧,∴﹣<0。∴>0。∴。故本选项错误。 B、∵二次函数的图象对称轴:,∴,。故本选项错误。 C、从图象可知,当时,。故本选项错误。 D、∵二次函数的图象对称轴为,与轴的一个交点的取值范围为1>1, ∴二次函数的图象与轴的另一个交点的取值范围为2<﹣2。 ∴当时,,即。故本选项正确。 故选D。 2. (2012浙江衢州3分)已知二次函数y=﹣x2﹣7x+,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是【 】 A.y1>y2>y3 B.y1<y2<y3 C.y2>y3>y1 D.y2<y3<y1 【答案】A。 【考点】二次函数图象上点的坐标特征。 【分析】根据x1、x2、x3与对称轴的大小关系,判断y1、y2、y3的大小关系: ∵二次函数,∴此函数的对称轴为:。 ∵<0<x1<x2<x3,三点都在对称轴右侧,a<0, ∴对称轴右侧y随x的增大而减小。∴y1>y2>y3。故选A。 3. (2012浙江义乌3分)如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: ①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小; ③使得M大于2的x值不存在; ④使得M=1的x值是或. 其中正确的是【 】 A.①② B.①④ C.②③ D.③④ 【答案】D。 【考点】二次函数的图象和性质。 【分析】①∵当x>0时,利用函数图象可以得出y2>y1。∴此判断错误。 ②∵抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2, 若y1≠y2,取y1、y2中的较小值记为M。 ∴当x<0时,根据函数图象可以得出x值越大,M值越大。∴此判断错误。 ③∵抛物线y1=﹣2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2), 当x=0时,M=2,抛物线y1=﹣2x2+2,最大值为2,故M大于2的x值不存在;∴此判断正确。 ④ ∵使得M=1时, 若y1=﹣2x2+2=1,解得:x1=,x2=﹣; 若y2=2x+2=1,解得:x=﹣。 由图象可得出:当x=>0,此时对应y1=M。 ∵抛物线y1=﹣2x2+2与x轴交点坐标为:(1,0),(﹣1,0), ∴当﹣1<x<0,此时对应y2=M, ∴M=1时,x=或x=﹣。∴此判断正确。 因此正确的有:③④。故选D。 4. (2012江苏常州2分)已知二次函数,当自变量x分别取,3,0时,对应的值分别为,则的大小关系正确的是【 】 A. B. C. D. 【答案】 B。 【考点】二次函数的图象和性质。 【分析】由二次函数知, 它的图象开口向上,对称轴为x=2,如图所示。 根据二次函数的对称性,x=3和x=1时,y值相等。 由于二次函数在对称轴x=2左侧,y随x的增大而减小,而0<1<,因此,。故选B。 5. (2012江苏镇江3分)关于x的二次函数,其图象的对称轴在y轴的右侧,则实数m的取值范围是【 】 A. B. C. D. 【答案】D。 【考点】二次函数的性质。 【分析】∵, ∴它的对称轴为。 又∵对称轴在y轴的右侧, ∴。故选D。 5. (2012湖北天门、仙桃、潜江、江汉油田3分)已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有【 】 A.3个 B.2个 C.1个 D.0个 【答案】A。 【考点】二次函数图象与系数的关系。 【分析】根据图象可得:a>0,c>0,对称轴:。 ①∵它与x轴的两个交点分别为(﹣1,0),(3,0),∴对称轴是x=1, ∴。∴b+2a=0。故命题①错误。 ②∵a>0,,∴b<0。 又c>0,∴abc<0。故命题②正确。 ③∵b+2a=0,∴a﹣2b+4c=a+2b﹣4b+4c=﹣4b+4c。 ∵a﹣b+c=0,∴4a﹣4b+4c=0。∴﹣4b+4c=﹣4a。 ∵a>0,∴a﹣2b+4c=﹣4b+4c=﹣4a<0。故命题③正确。 ④根据图示知,当x=4时,y>0,∴16a+4b+c>0。 由①知,b=﹣2a,∴8a+c>0。故命题④正确。 ∴正确的命题为:①②③三个。故选A。 6. (2012湖北宜昌3分)已知抛物线y=ax2﹣2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是【 】 A.第四象限 B.第三象限 C.第二象限 D.第一象限 【答案】D。 【考点】抛物线与x轴的交点与对应的一元二次方程的解之间的关系,二次函数的性质。1419956 【分析】∵抛物线y=ax2﹣2x+1与x轴没有交点,∴△=4﹣4a<0,解得:a>1。 ∴抛物线的开口向上。 又∵b=﹣2,∴抛物线的对称轴在y轴的右侧。 ∴抛物线的顶点在第一象限。故选D。 7. (2012湖南郴州3分)抛物线的顶点坐标是【 】 A.(-1,2) B.(-1,-2) C.(1,-2) D.(1,2) 【答案】D。 【考点】二次函数的性质。 【分析】直接利用顶点式的特点可写出顶点坐标: ∵顶点式y=a(x-h)2+k,顶点坐标是(h,k), ∴抛物线的顶点坐标是(1,2)。故选D。 8. (2012湖南衡阳3分)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法: ①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0 其中正确的个数为【 】 A.1 B.2 C.3 D.4 【答案】C。 【考点】二次函数图象与系数的关系。 【分析】由抛物线的开口方向判断a与0的关系,由x=1时的函数值判断a+b+c>0,然后根据对称轴推出2a+b与0的关系,根据图象判断﹣1<x<3时,y的符号: ①∵图象开口向下,∴a<0。说法错误。 ②∵对称轴为x=,∴,即2a+b=0。说法正确。 ③当x=1时,y>0,则a+b+c>0。说法正确。 ④由图可知,当﹣1<x<3时,y>0。说法正确。 ∴说法正确的有3个。故选C。 9. (2012湖南株洲3分)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=﹣1,则该抛物线与x轴的另一交点坐标是【 】 A.(﹣3,0) B.(﹣2,0) C.x=﹣3 D.x=﹣2 【答案】A。 【考点】抛物线与x轴的交点,二次函数的对称性。 【分析】设抛物线与x轴的另一个交点为B(b,0), ∵抛物线与x轴的一个交点A(1,0),对称轴是x=﹣1, ∴=﹣1,解得b=﹣3。∴B(﹣3,0)。故选A。 10. (2012四川乐山3分)二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是【 】 A.0<t<1 B.0<t<2 C.1<t<2 D.﹣1<t<1 【答案】B。 【考点】二次函数图象与系数的关系。 【分析】∵二次函数y=ax2+bx+1的顶点在第一象限,且经过点(﹣1,0), ∴a﹣b+1=0,a<0,b>0, ∵由a=b﹣1<0得b<1,∴0<b<1①, ∵由b=a+1>0得a>﹣1,∴﹣1<a<0②。 ∴由①②得:﹣1<a+b<1。∴0<a+b+1<2,即0<t<2。故选B。 11. (2012四川广元3分) 若二次函数(a,b为常数)的图象如图,则a的值为 【 】 A. 1 B. C. D. -2 【答案】C。 【考点】二次函数图象上点的坐标特征 【分析】由图可知,函数图象开口向下,∴a<0, 又∵函数图象经过坐标原点(0,0),∴a2-2=0,解得a1= (舍去),a2=-。故选C。 12. (2012四川德阳3分)设二次函数,当时,总有,当时,总有, 那么c的取值范围是【 】 A. B. C. D. 【答案】B。 【考点】二次函数的性质。 【分析】∵当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0, ∴当x=1时,y=0,即1+b+c=0①。 ∵当1≤x≤3时,总有y≤0, ∴当x=3时,y=9+3b+c≤0②。 ①②联立解得:c≥3。故选B。 13. (2012四川巴中3分) 对于二次函数,下列说法正确的是【 】 A. 图象的开口向下 B. 当x>1时,y随x的增大而减小 C. 当x<1时,y随x的增大而减小 D. 图象的对称轴是直线x=-1 【答案】C。 【考点】二次函数的性质。 【分析】把二次函数化为顶点式的形式,根据二次函数的性质进行解答: 二次函数, A、∵此二次函数中a=2>0,∴抛物线开口向上,故本选项错误; B、∵由二次函数的解析式可知,此抛物线开口向上,对称轴为x=1,∴当x>1时,y随x的增 大而增大,故本选项错误; C、∵由二次函数的解析式可知,此抛物线开口向上,对称轴为x=1,∴当x<1时,y随x的增 大而减小,故本选项正确; D、由二次函数的解析式可知抛物线对称轴为x=1,故本选项错误。 故选C。 14. (2012辽宁鞍山3分)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是【 】 A.①④ B.①③ C.②④ D.①② 15. (2012山东滨州3分)抛物线 与坐标轴的交点个数是【 】 A.3 B.2 C.1 D.0 【答案】A。 【考点】抛物线与轴的交点,解一元一次、二次方程。 【分析】∵抛物线解析式, 令,解得:,∴抛物线与轴的交点为(0,4), 令,得到, ∴抛物线与轴的交点分别为(,0),(1,0)。 综上,抛物线与坐标轴的交点个数为3。故选A。 16. (2012山东济南3分)如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】 A.y的最大值小于0 B.当x=0时,y的值大于1 C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0 【答案】D。 【考点】二次函数的图象和性质。 【分析】根据图象的对称轴的位置、增减性及开口方向直接作答:由图象知, A、点(1,1)在图象的对称轴的左边,所以y的最大值大于1,不小于0;故本选项错误; B、当x=0时,y的值就是函数图象与y轴的交点,而图象与y轴的交点在(1,1)点的左边, 故y<1,故本选项错误; C、对称轴在(1,1)的右边,在对称轴的左边y随x的增大而增大,∵-1<1,∴x=-1时,y 的值小于x=1时,y的值1,即当x=-1时,y的值小于1;故本选项错误; D、当x=-3时,函数图象上的点在点(-2,-1)的左边,所以y的值小于0;故本选项正确。 故选D。 17. (2012山东日照4分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是【 】 (A) ①② (B) ②③ (C) ③④ (D)①④ 【答案】D。 【考点】二次函数图象与系数的关系,一元二次方程根的判别式,二次函数的性质,。 【分析】根据二次函数图象和性质分别作出判断: ∵二次函数图象与x轴有两个交点,∴对应的一元二次方程ax2+bx+c 有两个不相等的实数根。 ∴b2-4ac>0。选项①正确。 又∵对称轴为直线x=1,即,∴2a+b=0。选项②错误。 ∵由图象知,x=-2对应的函数值为负数,∴当x=-2时,y=4a-2b+c<0。选项 ③错误。 ∵图象知,x=-1对应的函数值为0,∴当x=-1时,y=a+b+c=0。 联立2a+b=0和y=a+b+c=0可得:b=-2a,c=-3a。 ∴a:b:c=a:(-2a):(-3a)=-1:2:3。选项④正确。 综上所述,正确的选项有:①④。故选D。 18. (2012山东泰安3分)二次函数的图象如图,若一元二次方程有实数根,则的最大值为【 】 A. B.3 C. D.9 【答案】B。 【考点】抛物线与轴的交点。 【分析】∵抛物线的开口向上,顶点纵坐标为﹣3, ∴>0,,即。 ∵一元二次方程有实数根, ∴△=,即,即,解得。 ∴的最大值为3。故选B。 19. (2012山东泰安3分)设A,B,C是抛物线上的三点,则,,的大小关系为【 】 A. B. C. D. 【答案】 A。 【考点】二次函数图象上点的坐标特征。 【分析】∵函数的解析式是,如右图, ∴对称轴是。 ∴点A关于对称轴的点A′是。, 那么点A′、B、C都在对称轴的右边,而对称轴右边随的增大而减小, ∴于是。故选A。 20. (2012山东威海3分)已知二次函数的图象如图所示,下列结论错误的是【 】 A.abc>0 B.3a>2b C.m(am+b)≤a-b D.4a-2b+c<0 【答案】D。 【考点】二次函数的图象和性质,不等式的性质。 【分析】∵二次函数的图象的开口向下,对称轴为x=-1,与y轴的交点在x轴上方, ∴a<0,c>0,且,即b=2a<0。 ∴abc>0。结论A正确。 ∵3a-2b=3a-4a=-a>0,∴3a>2b。结论B正确。 ∵., ∴m(am+b)≤a-b。结论C正确。 从图象可知,当x=-2时,y>0,即4a-2b+c>0。结论D错误。 故选D。 21. (2012山东烟台3分)已知二次函数y=2(x﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.则其中说法正确的有【 】 A.1个 B.2个 C.3个 D.4个 【答案】A。 【考点】二次函数的性质。 【分析】结合二次函数解析式,根据函数的性质对各小题分析判断解答即可: ①∵2>0,∴图象的开口向上,故本说法错误; ②图象的对称轴为直线x=3,故本说法错误; ③其图象顶点坐标为(3,1),故本说法错误; ④当x<3时,y随x的增大而减小,故本说法正确。 综上所述,说法正确的有④共1个。故选A。 22. (2012山东枣庄3分)抛物线经过点(2,4),则代数式的值为【 】 A.3 B.9 C. D. 【答案】C。 【考点】曲线上点的坐标与方程的关系,求代数式的值。 【分析】∵抛物线经过点(2,4),∴,即。 ∴。故选C。 23. (2012河北省3分)如图,抛物线y1=a(x+2)2-3与y2=(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是【 】 A.①② B.②③ C.③④ D.①④ 【答案】D。 【考点】二次函数的性质,曲线上点的坐标与方程的关系,解一元二次方程。 【分析】∵(x-3)2≥0,∴y2=(x-3)2+1>0,即无论x取何值,y2的值总是正数。故结论①正确。 ∵ 两抛物线交于点A(1,3),∴3=a(1+2)2-3,解得a=≠1。故结论②错误。 【至此即可判断D正确】 当x=0时,y2-y1=[(0-3)2+1]-[(0+2)2-3]= 。故结论③错误。 解3=(x+2)2-3得x=1或x=-5,∴B(1,-5)。∴AB=6,2AB=12。 解3=(x-3)2+1得x=1或x=5,∴B(1, 5)。∴BC=4,3BC=12。 ∴2AB=3AC。故结论④正确。 因此,正确结论是①④。故选D。 24. (2012甘肃白银3分)二次函数的图象如图所示,则函数值时x的取值范围是【 】 A. B.x>3 C.-1<x<3 D.或x>3 【答案】C。 【考点】二次函数的图象 【分析】根据y<0,则函数图象在x轴的下方,所以找出函数图象在x轴下方的x的取值范围即可: 由图象可知,当-1<x<3时,函数图象在x轴的下方,y<0。故选C。 25. (2012甘肃兰州4分)抛物线y=-2x2+1的对称轴是【 】 A.直线 B.直线 C.y轴 D.直线x=2 【答案】C。 【考点】二次函数的性质。 【分析】已知抛物线解析式为顶点式,可直接写出顶点坐标及对称轴: ∵抛物线y=-2x2+1的顶点坐标为(0,1),∴对称轴是直线x=0(y轴)。故选C。 26. (2012甘肃兰州4分)已知二次函数y=a(x+1)2-b(a≠0)有最小值,则a,b 的大小关系为【 】 A.a>b B.a<b C.a=b D.不能确定 【答案】D。 【考点】二次函数的最值。 【分析】∵二次函数y=a(x+1)2-b(a≠0)有最小值,∴a>0。 ∵无论b为何值,此函数均有最小值,∴a、b的大小无法确定。故选D。 27. (2012青海西宁3分)如图,二次函数y=ax2+bx+c的图象过点(-1,1)、(2,-1).下列关于这个 二次函数的叙述正确的是【 】 A.当x=0时,y的值大于1 B.当x=3时,y的值小于0 C.当x=1时,y的值大于1 D.y的最大值小于0 28. (2012黑龙江黑河、齐齐哈尔、大兴安岭、鸡西3分)已知二次函数y=ax2+bx+c(a≠O)的图象如图所示,现有下列结论:①abc>0 ②b2-4ac<0 ⑤c<4b ④a+b>0,则其中正确结论的个数是【 】 A.1个 B.2个 C.3个 D.4个 【答案】B。 【考点】二次函数图象与系数的关系。 【分析】由抛物线的开口向下,得到a<0, ∵>0,∴b>0。 又∵抛物线与y轴交于正半轴,∴c>0。 ∴abc<0。结论①错误。 又∵抛物线与x轴有2个交点,∴b2-4ac>0。结论②错误。 又∵对称轴为直线x=1,∴,即b=-2a。结论④正确。 ∵当x=-2时,对应的函数值y<0, ∴4a-2b+c<0,即-2b-2b+c<0,即c<<4b。结论③正确。 ∴其中正确的结论有③④。故选B。 29. (2012黑龙江牡丹江3分)抛物线与x轴的交点坐标是(-l,0)和(3,0),则这条抛物线的对称轴是【 】. A.直线x=-1 8.直线x=0 C.直线x=1 D.直线x= 3 【答案】C。 【考点】曲线上点的坐标与方程的关系,二次函数的性质。 【分析】由抛物线与x轴的交点坐标是(-l,0)和(3,0),根据二次函数的性质,得这条抛物线的对称轴是x=。故选C。 二、填空题 1. (2012广东深圳3分)二次函数的最小值是 ▲ . 【答案】5。 【考点】二次函数的性质。 【分析】∵,∴当时,函数有最小值5。 2. (2012江苏苏州3分)已知点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,若 x1>x2>1,则y1 ▲ y2. 【答案】>。 【考点】二次函数图象上点的坐标特征,二次函数的性质。 【分析】由二次函数y=(x-1)2+1知,其对称轴为x=1。 ∵x1>x2>1,∴两点均在对称轴的右侧。 ∵此函数图象开口向上,∴在对称轴的右侧y随x的增大而增大。 ∵x1>x2>1,∴y1>y2。 3. (2012江苏无锡2分)若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为 ▲ . 【答案】y=﹣x2+4x﹣3。 【考点】待定系数法,曲线上点的坐标与方程的关系。 【分析】∵抛物线y=ax2+bx+c的顶点是A(2,1),∴可设抛物线的解析式为y=a(x﹣2)2+1。 又∵抛物线y=a(x﹣2)2+1经过点B(1,0),∴(1,0)满足y=a(x﹣2)2+1。 ∴将点B(1,0)代入y=a(x﹣2)2得,0=a(1﹣2)2即a=﹣1。 ∴抛物线的函数关系式为y=﹣(x﹣2)2+1,即y=﹣x2+4x﹣3。 4. (2012湖北咸宁3分)对于二次函数,有下列说法: ①它的图象与轴有两个公共点; ②如果当≤1时随的增大而减小,则; ③如果将它的图象向左平移3个单位后过原点,则; ④如果当时的函数值与时的函数值相等,则当时的函数值为. 其中正确的说法是 ▲ .(把你认为正确说法的序号都填上) 【答案】①④。 【考点】二次函数的性质,一元二次方程的判别式,平移的性质。 【分析】由得, ∴方程有两不相等的实数根,即二次函数 的图象与轴有两个公共点。故说法①正确。 ∵的对称轴为,而当≤1时随的增大而减小, ∴。故说法②错误。 ∵ , ∴将它的图象向左平移3个单位后得。 ∵经过原点,∴,解得。故说法③错误。 ∵由时的函数值与时的函数值相等,得, 解得, ∴当时的函数值为。故说法④正确。 综上所述,正确的说法是①④。 5. (2012湖北孝感3分)二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如 图所示.下列说法正确的是 ▲ (填正确结论的序号). ①abc<0;②a-b+c<0;③3a+c<0;④当-1<x<3时,y>0. 【答案】①②③。 【考点】二次函数图象与系数的关系。 【分析】由二次函数的图象可得:a>0,b<0,c>0,对称轴x=1,则再结合图象判断正确的选项即可: 由a>0,b<0,c>0得abc<0,故结论①正确。 ∵由二次函数的图象可得x=2.5时,y=0,对称轴x=1,∴x=-0.5时,y=0。 ∴x=-1时,y<0,即a-b+c<0。故结论②正确。 ∵二次函数的图象的对称轴为x=1,即,∴。 代入②a-b+c<0得3a+c<0。故结论③正确。 ∵由二次函数的图象和②可得,当-0.5<x<2.5时,y>0;当x<-0.5或 x>2.5时,y<0。 ∴当-1<x<3时,y>0不正确。故结论④错误。 综上所述,说法正确的是①②③。 6. (2012辽宁营口3分)二次函数的部分图像如图所示,若关于的一元二次方程 的一个解为,则另一个解= ▲ . 【答案】5。 【考点】二次函数的性质,二次函数与轴的交点和对应的一元二次方程的关系。 【分析】∵二次函数的对称轴为 ∴关于的对称点是5。∴的另一个解=5。 7. (2012山东枣庄4分)二次函数的图象如图所示.当y<0时,自变量x的取值范围是 ▲ . 【答案】-1<x<3。 【考点】二次函数与不等式(组) 【分析】根据二次函数的性质得出,y<0,即是图象在x轴下方部分,从而得出x的取值范围: ∵二次函数y=x2-2x-3的图象如图所示, ∴图象与x轴交在(-1,0),(3,0), ∴当y<0时,即图象在x轴下方的部分,此时x的取值范围是:-1<x<3。 8. (2012新疆区5分)当x= ▲ 时,二次函数y=x2+2x﹣2有最小值. 【答案】﹣1。 【考点】二次函数的最值。 【分析】用配方法把函数化为顶点式的形式,再根据其解析式即可求解: ∵二次函数y=x2+2x﹣2可化为y=(x+1)2﹣3, ∴当x=﹣1时,二次函数y=x2+2x﹣2有最小值。(或用公式求解) 9. (2012吉林长春3分)如图,在平面直角坐标系中,点A是抛物线与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为 ▲ . 【答案】18。 【考点】二次函数的性质,等边三角形的性质。 【分析】根据二次函数的性质,抛物线的对称轴为x=3。 ∵A是抛物线与y轴的交点,点B是这条抛物线上的另一 点,且AB∥x轴。 ∴A,B关于x=3对称。∴AB=6。 又∵△ABC是等边三角形,∴以AB为边的等边三角形ABC的周长为6×3=18。 10. (2012黑龙江牡丹江3分)若抛物线经过点(-1,10),则= ▲ . 【答案】10。 【考点】曲线上点的坐标与方程的关系。 【分析】由抛物线经过点(-1,10),根据点在曲线上,点的坐标满足方程的关系,将 (-1,10)代入得,即。 11. (2012黑龙江大庆3分)已知二次函数y=-x-2x+3的图象上有两点A(-7,),B(-8,),则 ▲ .(用>、<、=填空). 【答案】>。 【考点】二次函数的性质和图象上点的坐标特征。119281 【分析】根据已知条件求出二次函数的对称轴和开口方向,再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系: ∵二次函数y=﹣x2﹣2x+3的对称轴是x=﹣1,开口向下, ∴在对称轴的左侧y随x的增大而增大。 ∵点A(﹣7,y1),B(﹣8,y2)是二次函数y=﹣x2﹣2x+3的图象上的两点,且﹣7>﹣8, ∴y1>y2。 三、解答题 1. (2012北京市7分)已知二次函数在和时的函数值相等。 (1) 求二次函数的解析式; (2) 若一次函数的图象与二次函数的图象都经过点A,求m和k的值; (3) 设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间 的部分(含点B和点C)向左平移个单位后得到的图象记为C,同时将(2)中得到的直线向上平移n个单位。请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围。 【答案】解:(1)∵二次函数在和时的函数值相等,∴二次函数图象的对称轴为。 ∴,解得。 ∴二次函数解析式为。 (2)∵二次函数图象经过A点, ∴,A(-3,-6)。 又∵一次函数的图象经过A点, ∴,解得。 (3)由题意可知,二次函数在点B,C间的部分图象的解析式为 ,, 则向左平移后得到的图象C的解析式为,。 此时一次函数的图象平移后的解析式为。 ∵平移后的直线与图象C有公共点,∴两个临界的交点为与。 ∴当时,,即; 当时,,即。 ∴ 【考点】二次函数综合题,二次函数的性质,曲线上点的坐标与方程的关系,平移的性质。 【分析】(1)由二次函数在和时的函数值相等,可知二次函数图象的对称轴为,从而由对称轴公式可求得,从而求得二次函数的解析式。 (2)由二次函数图象经过A点代入可求得,从而由一次函数的图象经过A点,代入可求得。 (3)根据平移的性质,求得平移后的二次函数和一次函数表达式,根据平移后的直线与图象C有公共点,求得公共点的坐标即可。 2. (2012广东佛山8分)(1)任选以下三个条件中的一个,求二次函数y=ax2+bx+c的解析式; ①y随x变化的部分数值规律如下表: x -1 0 1 2 3 y 0 3 4 3 0 ②有序数对(-1,0),(1,4),(3,0)满足y=ax2+bx+c; ③已知函数y=ax2+bx+c的图象的一部分(如图). (2)直接写出二次函数y=ax2+bx+c的三个性质. 3. (2012广东梅州10分)(1)已知一元二次方程x2+px+q=0(p2﹣4q≥0)的两根为x1、x2;求证:x1+x2=﹣p,x1•x2=q. (2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(﹣1,﹣1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值. 【答案】(1)证明:∵a=1,b=p,c=q,p2﹣4q≥0, ∴。 (2)解:把(﹣1,﹣1)代入y=x2+px+q得p﹣q=2,即q=p﹣2。 设抛物线y=x2+px+q与x轴交于A、B的坐标分别为(x1,0)、(x2,0)。 ∵d=|x1﹣x2|, ∴d2=(x1﹣x2)2=(x1+x2)2﹣4 x1•x2=p2﹣4q=p2﹣4p+8=(p﹣2)2+4。 ∴当p=2时,d 2的最小值是4。 【考点】一元二次方程根的判别式和根与系数的关系,抛物线与x轴的交点,曲线上点的坐标与方程的关系,二次函数的最值。 【分析】(1)根据一元二次方程根与系数的关系可直接证得。 【教材中没有元二次方程根与系数的关系可先根据求根公式得出x1、x2的值,再求出两根的和与积即可】 (2)把点(﹣1,﹣1)代入抛物线的解析式,再由d=|x1﹣x2|可得d2关于p的函数关系式,应用二次函数的最值原理即可得出结论。 4. (2012浙江杭州8分)当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值. 【答案】解:∵当开口向下时函数y=(k﹣1)x2﹣4x+5﹣k取最大值 ∴k﹣1<0,解得k<1。 ∴当k=﹣1时函数y=(k﹣1)x2﹣4x+5﹣k有最大值,当k=1,2时函数没有最大值。 ∴当k=﹣1时,函数y=﹣2x2﹣4x+6=﹣2(x+1)2+8。 ∴最大值为8。 【考点】二次函数的最值。 【分析】首先根据函数有最大值得到k的取值范围,然后判断即可。求最大值时将函数解析式化为顶点式或用公式即可。 5. (2012江苏徐州8分)二次函数的图象经过点(4,3),(3,0)。 (1)求b、c的值; (2)求出该二次函数图象的顶点坐标和对称轴; (3)在所给坐标系中画出二次函数的图象。 【答案】解:(1)∵二次函数的图象经过点(4,3),(3,0), ∴,解得。 (2)∵该二次函数为。 ∴该二次函数图象的顶点坐标为(2,-1),对称轴为x=1。 (3)列表如下: x ··· 0 1 2 3 4 ··· y ··· 3 0 1 0 3 ··· 描点作图如下: 【考点】曲线上点的坐标与方程的关系,二次函数的性质,描点作图。 【分析】(1)根据点在曲线上,点的坐标满足方程的关系,将(4,3),(3,0)代入得关于b、c的方程组,解之即得。 (2)求出二次函数的顶点式(或用公式法)即可求得该二次函数图象的顶点坐标和对称轴。 (3)描点作图。 6. (2012湖北荆州12分)已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点. (1)求k的取值范围; (2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2. ①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最大值. 【答案】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点。 当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点, 令y=0得(k﹣1)x2﹣2kx+k+2=0. △=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1。 综上所述,k的取值范围是k≤2。 (2)①∵x1≠x2,由(1)知k<2且k≠1。 由题意得(k﹣1)x12+(k+2)=2kx1(*), 将(*)代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2。 又∵x1+x2=,x1x2=,∴2k•=4•, 解得:k1=﹣1,k2=2(不合题意,舍去)。∴所求k值为﹣1。 ②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+,且﹣1≤x≤1, 由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=。 ∴y的最大值为,最小值为﹣3。 【考点】抛物线与x轴的交点,一次函数的定义,一元二次方程根的判别式和根与系数物关系,二次函数的最值。 【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0。 (2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k的值。②充分利用图象,直接得出y的最大值和最小值。 7. (2012山东淄博8分)已知:抛物线. (1)写出抛物线的对称轴; (2)完成下表; x … −7 −3 1 3 … y … −9 −1 … (3)在下面的坐标系中描点画出抛物线的图象. 【答案】解:(1)抛物线的对称轴为x=-1。 (2)填表如下: x … −7 -5 −3 -1 1 3 5 … y … −9 -4 -1 0 −1 -4 -9 … (3)描点作图如下: 【考点】二次函数的图象和性质。 【分析】(1)直接根据顶点式写出抛物线的对称轴。 (2)根据抛物线的对称填表。 (3)描点作图。 8. (2012黑龙江牡丹江6分)如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题: (1)求抛物线的解析式; (2)若与轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点D,使得△ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由 注:抛物线的对称轴是查看更多