- 2021-05-10 发布 |
- 37.5 KB |
- 45页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学分类汇编考点锐角三角函数和解直角三角形
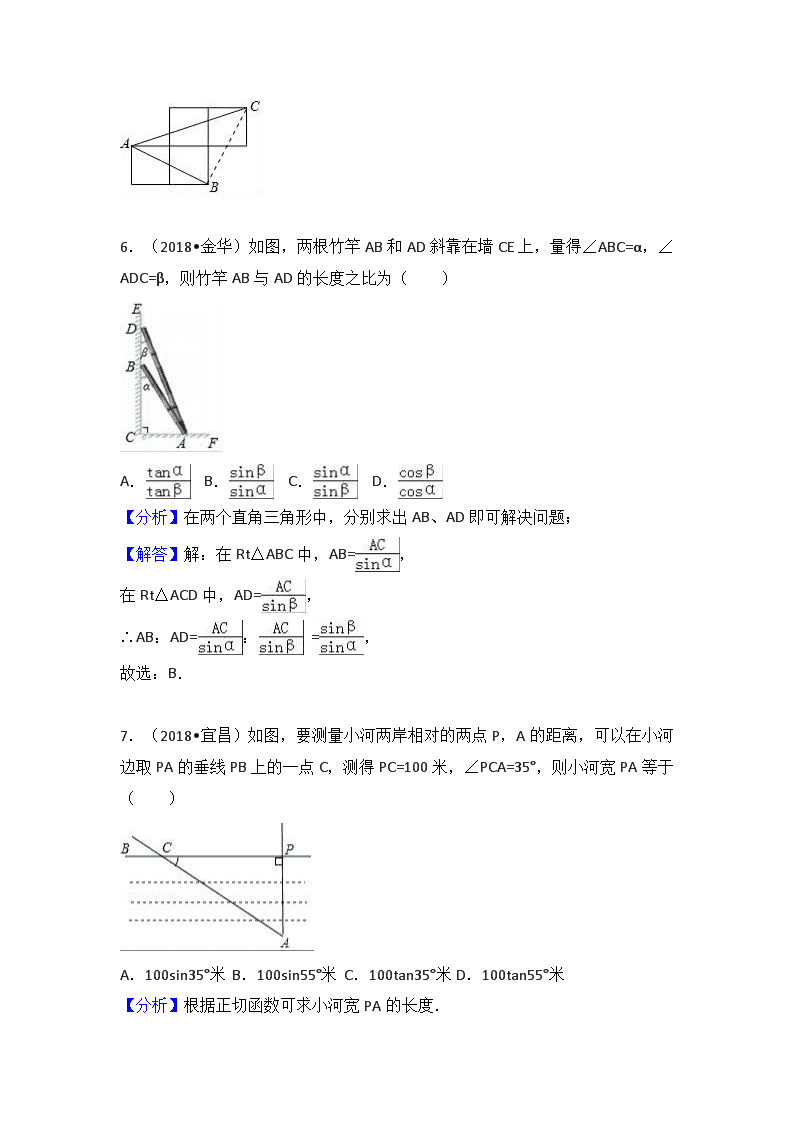
2018中考数学试题分类汇编:考点37锐角三角函数和解直角三角形 一.选择题(共15小题) 1.(2018•柳州)如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB==( ) A. B. C. D. 【分析】首先利用勾股定理计算出AB长,再计算sinB即可. 【解答】解:∵∠C=90°,BC=4,AC=3, ∴AB=5, ∴sinB==, 故选:A. 2.(2018•孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( ) A. B. C. D. 【分析】先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 【解答】解:在Rt△ABC中,∵AB=10、AC=8, ∴BC===6, ∴sinA===, 故选:A. 3.(2018•大庆)2cos60°=( ) A.1 B. C. D. 【分析】直接利用特殊角的三角函数值进而计算得出答案. 【解答】解:2cos60°=2×=1. 故选:A. 4.(2018•天津)cos30°的值等于( ) A. B. C.1 D. 【分析】根据特殊角的三角函数值直接解答即可. 【解答】解:cos30°=. 故选:B. 5.(2018•贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( ) A. B.1 C. D. 【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【解答】解:连接BC, 由网格可得AB=BC=,AC=,即AB2+BC2=AC2, ∴△ABC为等腰直角三角形, ∴∠BAC=45°, 则tan∠BAC=1, 故选:B. 6.(2018•金华)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( ) A. B. C. D. 【分析】在两个直角三角形中,分别求出AB、AD即可解决问题; 【解答】解:在Rt△ABC中,AB=, 在Rt△ACD中,AD=, ∴AB:AD=: =, 故选:B. 7.(2018•宜昌)如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( ) A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米 【分析】根据正切函数可求小河宽PA的长度. 【解答】解:∵PA⊥PB,PC=100米,∠PCA=35°, ∴小河宽PA=PCtan∠PCA=100tan35°米. 故选:C. 8.(2018•威海)如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( ) A.当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m B.小球距O点水平距离超过4米呈下降趋势 C.小球落地点距O点水平距离为7米 D.斜坡的坡度为1:2 【分析】求出当y=7.5时,x的值,判定A;根据二次函数的性质求出对称轴,根据二次函数性质判断B;求出抛物线与直线的交点,判断C,根据直线解析式和坡度的定义判断D. 【解答】解:当y=7.5时,7.5=4x﹣x2, 整理得x2﹣8x+15=0, 解得,x1=3,x2=5, ∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5侧面cm,A错误,符合题意; y=4x﹣x2 =﹣(x﹣4)2+8, 则抛物线的对称轴为x=4, ∴当x>4时,y随x的增大而减小,即小球距O点水平距离超过4米呈下降趋势,B正确,不符合题意; , 解得,,, 则小球落地点距O点水平距离为7米,C正确,不符合题意; ∵斜坡可以用一次函数y=x刻画, ∴斜坡的坡度为1:2,D正确,不符合题意; 故选:A. 9.(2018•淄博)一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α的度数时,具体按键顺序是( ) A. B. C. D. 【分析】先利用正弦的定义得到sinA=0.15,然后利用计算器求锐角α. 【解答】解:sinA===0.15, 所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为 故选:A. 10.(2018•重庆)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为( )(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6) A.12.6米 B.13.1米 C.14.7米 D.16.3米 【分析】如图延长AB交ED的延长线于M,作CJ⊥DM于J.则四边形BMJC是矩形.在Rt△CDJ中求出CJ、DJ,再根据,tan∠AEM=构建方程即可解决问题; 【解答】解:如图延长AB交ED的延长线于M,作CJ⊥DM于J.则四边形BMJC是矩形. 在Rt△CJD中, ==,设CJ=4k,DJ=3k, 则有9k2+16k2=4, ∴k=, ∴BM=CJ=,BC=MJ=1,DJ=,EM=MJ+DJ+DE=, 在Rt△AEM中,tan∠AEM=, ∴1.6=, 解得AB≈13.1(米), 故选:B. 11.(2018•重庆)如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( ) A.21.7米 B.22.4米 C.27.4米 D.28.8米 【分析】作BM⊥ED交ED的延长线于M,CN⊥DM于N.首先解直角三角形Rt△CDN,求出CN,DN,再根据tan24°=,构建方程即可解决问题; 【解答】解:作BM⊥ED交ED的延长线于M,CN⊥DM于N. 在Rt△CDN中,∵==,设CN=4k,DN=3k, ∴CD=10, ∴(3k)2+(4k)2=100, ∴k=2, ∴CN=8,DN=6, ∵四边形BMNC是矩形, ∴BM=CN=8,BC=MN=20,EM=MN+DN+DE=66, 在Rt△AEM中,tan24°=, ∴0.45=, ∴AB=21.7(米), 故选:A. 12.(2018•长春)如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为( ) A.800sinα米 B.800tanα米 C.米 D.米 【分析】在Rt△ABC中,∠CAB=90°,∠B=α,AC=800米,根据tanα=,即可解决问题; 【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米, ∴tanα=, ∴AB==. 故选:D. 13.(2018•香坊区)如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋楼底部C的俯角为60°,热气球A与楼的水平距离为120米,这栋楼的高度BC为( ) A.160米 B.(60+160) C.160米 D.360米 【分析】首先过点A作AD⊥BC于点D,根据题意得∠BAD=30°,∠CAD=60°,AD=120m,然后利用三角函数求解即可求得答案. 【解答】解:过点A作AD⊥BC于点D,则∠BAD=30°,∠CAD=60°,AD=120m, 在Rt△ABD中,BD=AD•tan30°=120×=40(m), 在Rt△ACD中,CD=AD•tan60°=120×=120(m), ∴BC=BD+CD=160(m). 故选:C. 14.(2018•绵阳)一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:≈1.732,≈1.414) A.4.64海里 B.5.49海里 C.6.12海里 D.6.21海里 【分析】根据题意画出图形,结合图形知∠BAC=30°、∠ACB=15°,作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°,设BD=x,则AB=BE=CE=2x、AD=DE=x,据此得出AC=2x+2x ,根据题意列出方程,求解可得. 【解答】解:如图所示, 由题意知,∠BAC=30°、∠ACB=15°, 作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°, 则∠BED=30°,BE=CE, 设BD=x, 则AB=BE=CE=2x,AD=DE=x, ∴AC=AD+DE+CE=2x+2x, ∵AC=30, ∴2x+2x=30, 解得:x=≈5.49, 故选:B. 15.(2018•苏州)如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( ) A.40海里 B.60海里 C.20海里 D.40海里 【分析】首先证明PB=BC,推出∠C=30°,可得PC=2PA,求出PA即可解决问题; 【解答】解:在Rt△PAB中,∵∠APB=30°, ∴PB=2AB, 由题意BC=2AB, ∴PB=BC, ∴∠C=∠CPB, ∵∠ABP=∠C+∠CPB=60°, ∴∠C=30°, ∴PC=2PA, ∵PA=AB•tan60°, ∴PC=2×20×=40(海里), 故选:D. 二.填空题(共17小题) 16.(2018•北京)如图所示的网格是正方形网格,∠BAC > ∠DAE.(填“>”,“=”或“<”) 【分析】作辅助线,构建三角形及高线NP,先利用面积法求高线PN=,再分别求∠BAC、∠DAE的正弦,根据正弦值随着角度的增大而增大,作判断. 【解答】解:连接NH,BC,过N作NP⊥AD于P, S△ANH=2×2﹣﹣×1×1=AH•NP, =PN, PN=, Rt△ANP中,sin∠NAP====0.6, Rt△ABC中,sin∠BAC===>0.6, ∵正弦值随着角度的增大而增大, ∴∠BAC>∠DAE, 故答案为:>. 17.(2018•滨州)在△ABC中,∠C=90°,若tanA=,则sinB= . 【分析】直接根据题意表示出三角形的各边,进而利用锐角三角函数关系得出答案. 【解答】解:如图所示: ∵∠C=90°,tanA=, ∴设BC=x,则AC=2x,故AB=x, 则sinB===. 故答案为:. 18.(2018•泰安)如图,在△ABC中,AC=6,BC=10,tanC=,点D是AC边上的动点(不与点C重合),过D作DE⊥BC,垂足为E,点F是BD的中点,连接EF,设CD=x,△DEF的面积为S,则S与x之间的函数关系式为 S= x2 . 【分析】可在直角三角形CED中,根据DE、CE的长,求出△BED的面积即可解决问题. 【解答】解:(1)在Rt△CDE中,tanC=,CD=x ∴DE=x,CE=x, ∴BE=10﹣x, ∴S△BED=×(10﹣x)•x=﹣x2+3x. ∵DF=BF, ∴S=S△BED=x2, 故答案为S=x2. 19.(2018•无锡)已知△ABC中,AB=10,AC=2,∠B=30°,则△ABC的面积等于 15或10 . 【分析】作AD⊥BC交BC(或BC延长线)于点D,分AB、AC位于AD异侧和同侧两种情况,先在Rt△ABD中求得AD、BD的值,再在Rt△ACD中利用勾股定理求得CD的长,继而就两种情况分别求出BC的长,根据三角形的面积公式求解可得. 【解答】解:作AD⊥BC交BC(或BC延长线)于点D, ①如图1,当AB、AC位于AD异侧时, 在Rt△ABD中,∵∠B=30°,AB=10, ∴AD=ABsinB=5,BD=ABcosB=5, 在Rt△ACD中,∵AC=2, ∴CD===, 则BC=BD+CD=6, ∴S△ABC=•BC•AD=×6×5=15; ②如图2,当AB、AC在AD的同侧时, 由①知,BD=5,CD=, 则BC=BD﹣CD=4, ∴S△ABC=•BC•AD=×4×5=10. 综上,△ABC的面积是15或10, 故答案为15或10. 20.(2018•香坊区)如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为 5 . 【分析】作辅助线,构建全等三角形和高线DH,设CM=a,根据等腰直角三角形的性质和三角函数表示AC和AM的长,根据三角形面积表示DH的长,证明△ADG≌△CDH(AAS),可得DG=DH=MG=,AG=CH=a+,根据AM=AG+MG,列方程可得结论. 【解答】解:过D作DH⊥BC于H,过A作AM⊥BC于M,过D作DG⊥AM于G, 设CM=a, ∵AB=AC, ∴BC=2CM=2a, ∵tan∠ACB=2, ∴=2, ∴AM=2a, 由勾股定理得:AC=a, S△BDC=BC•DH=10, =10, DH=, ∵∠DHM=∠HMG=∠MGD=90°, ∴四边形DHMG为矩形, ∴∠HDG=90°=∠HDC+∠CDG,DG=HM,DH=MG, ∵∠ADC=90°=∠ADG+∠CDG, ∴∠ADG=∠CDH, 在△ADG和△CDH中, ∵, ∴△ADG≌△CDH(AAS), ∴DG=DH=MG=,AG=CH=a+, ∴AM=AG+MG, 即2a=a++, a2=20, 在Rt△ADC中,AD2+CD2=AC2, ∵AD=CD, ∴2AD2=5a2=100, ∴AD=5或﹣5(舍), 故答案为:5.. 21.(2018•眉山)如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD= 2 . 【分析】首先连接BE,由题意易得BF=CF,△ACO∽△BKO,然后由相似三角形的对应边成比例,易得KO:CO=1:3,即可得OF:CF=OF:BF=1:2,在Rt△OBF中,即可求得tan∠BOF的值,继而求得答案. 【解答】解:如图,连接BE, ∵四边形BCEK是正方形, ∴KF=CF=CK,BF=BE,CK=BE,BE⊥CK, ∴BF=CF, 根据题意得:AC∥BK, ∴△ACO∽△BKO, ∴KO:CO=BK:AC=1:3, ∴KO:KF=1:2, ∴KO=OF=CF=BF, 在Rt△PBF中,tan∠BOF==2, ∵∠AOD=∠BOF, ∴tan∠AOD=2. 故答案为:2 22.(2018•德州)如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是 . 【分析】先根据勾股定理的逆定理判断出△ABC的形状,再由锐角三角函数的定义即可得出结论. 【解答】解:∵AB2=32+42=25、AC2=22+42=20、BC2=12+22=5, ∴AC2+BC2=AB2, ∴△ABC为直角三角形,且∠ACB=90°, 则sin∠BAC==, 故答案为:. 23.(2018•齐齐哈尔)四边形ABCD中,BD是对角线,∠ABC=90°,tan∠ABD=,AB=20,BC=10,AD=13,则线段CD= 17 . 【分析】作AH⊥BD于H,CG⊥BD于G,根据正切的定义分别求出AH、BH,根据勾股定理求出HD,得到BD,根据勾股定理计算即可. 【解答】解:作AH⊥BD于H,CG⊥BD于G, ∵tan∠ABD=, ∴=, 设AH=3x,则BH=4x, 由勾股定理得,(3x)2+(4x)2=202, 解得,x=4, 则AH=12,BH=16, 在Rt△AHD中,HD==5, ∴BD=BH+HD=21, ∵∠ABD+∠CBD=90°,∠BCH+∠CBD=90°, ∴∠ABD=∠CBH, ∴=,又BC=10, ∴BG=6,CG=8, ∴DG=BD﹣BG=15, ∴CD==17, 故答案为:17. 24.(2018•广州)如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC= . 【分析】根据直角三角形的性质解答即可. 【解答】解:∵旗杆高AB=8m,旗杆影子长BC=16m, ∴tanC=, 故答案为: 25.(2018•枣庄)如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为 6.2 米.(结果保留两个有效数字)【参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601】 【分析】根据题意和锐角三角函数可以求得BC的长,从而可以解答本题. 【解答】解:在Rt△ABC中, ∵∠ACB=90°, ∴BC=AB•sin∠BAC=12×0.515≈6.2(米), 答:大厅两层之间的距离BC的长约为6.2米. 故答案为:6.2. 26.(2018•广西)如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是 40 m(结果保留根号) 【分析】利用等腰直角三角形的性质得出AB=AD,再利用锐角三角函数关系得出答案. 【解答】解:由题意可得:∠BDA=45°, 则AB=AD=120m, 又∵∠CAD=30°, ∴在Rt△ADC中, tan∠CDA=tan30°==, 解得:CD=40(m), 故答案为:40. 27.(2018•宁波)如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 1200(﹣1) 米(结果保留根号). 【分析】在Rt△ACH和Rt△HCB中,利用锐角三角函数,用CH表示出AH、BH的长,然后计算出AB的长. 【解答】解:由于CD∥HB, ∴∠CAH=∠ACD=45°,∠B=∠BCD=30° 在Rt△ACH中,∵∴∠CAH=45° ∴AH=CH=1200米, 在Rt△HCB,∵tan∠B= ∴HB== ==1200(米). ∴AB=HB﹣HA =1200﹣1200 =1200(﹣1)米 故答案为:1200(﹣1) 28.(2018•黄石)如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为米,点A、D、E在同一水平直线上,则A、B两点间的距离是 100(1+) 米.(结果保留根号) 【分析】如图,利用平行线的性质得∠A=60°,∠B=45°,在Rt△ACD中利用正切定义可计算出AD=100,在Rt△BCD中利用等腰直角三角形的性质得BD=CD=100,然后计算AD+BD即可. 【解答】解:如图, ∵无人机在空中C处测得地面A、B两点的俯角分别为60°、45°, ∴∠A=60°,∠B=45°, 在Rt△ACD中,∵tanA=, ∴AD==100, 在Rt△BCD中,BD=CD=100, ∴AB=AD+BD=100+100=100(1+). 答:A、B两点间的距离为100(1+)米. 故答案为100(1+). 29.(2018•咸宁)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为 300 m(结果保留整数,≈1.73). 【分析】在Rt△ABD中,根据正切函数求得BD=AD•tan∠BAD,在Rt△ACD中,求得CD=AD•tan∠CAD,再根据BC=BD+CD,代入数据计算即可. 【解答】解:如图,∵在Rt△ABD中,AD=90,∠BAD=45°, ∴BD=AD=110(m), ∵在Rt△ACD中,∠CAD=60°, ∴CD=AD•tan60°=110×=190(m), ∴BC=BD+CD=110+190=300(m) 答:该建筑物的高度BC约为300米. 故答案为300. 30.(2018•天门)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)n mile处,则海岛A,C之间的距离为 18 n mile. 【分析】作AD⊥BC于D,根据正弦的定义、正切的定义分别求出BD、CD,根据题意列式计算即可. 【解答】解:作AD⊥BC于D, 设AC=x海里, 在Rt△ACD中,AD=AC×sin∠ACD=x, 则CD=x, 在Rt△ABD中,BD=x, 则x+x=18(1+),解得,x=18, 答:A,C之间的距离为18海里. 故答案为:18 31.(2018•潍坊)如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号) 【分析】如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,通过解直角△AQP、直角△BPQ求得PQ的长度,即MN的长度,然后通过解直角△BMN求得BM的长度,则易得所需时间. 【解答】解:如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N, 在直角△AQP中,∠PAQ=45°,则AQ=PQ=60×1.5+BQ=90+BQ(海里), 所以 BQ=PQ﹣90. 在直角△BPQ中,∠BPQ=30°,则BQ=PQ•tan30°=PQ(海里), 所以 PQ﹣90=PQ, 所以 PQ=45(3+)(海里) 所以 MN=PQ=45(3+)(海里) 在直角△BMN中,∠MBN=30°, 所以 BM=2MN=90(3+)(海里) 所以 =(小时) 故答案是:. 32.(2018•济宁)如图,在一笔直的海岸线l上有相距2km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是 km. 【分析】首先由题意可证得:△ACB是等腰三角形,即可求得BC的长,然后由在Rt△CBD中,CD=BC•sin60°,求得答案. 【解答】解:过点C作CD⊥AB于点D, 根据题意得:∠CAD=90°﹣60°=30°,∠CBD=90°﹣30°=60°, ∴∠ACB=∠CBD﹣∠CAD=30°, ∴∠CAB=∠ACB, ∴BC=AB=2km, 在Rt△CBD中,CD=BC•sin60°=2×=(km). 故答案为:. 三.解答题(共18小题) 33.(2018•贵阳)如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法: ∵sinA=,sinB= ∴c=,c= ∴= 根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程. 【分析】三式相等,理由为:过A作AD⊥BC,BE⊥AC,在直角三角形ABD中,利用锐角三角函数定义表示出AD,在直角三角形ADC中,利用锐角三角函数定义表示出AD,两者相等即可得证. 【解答】解: ==,理由为: 过A作AD⊥BC,BE⊥AC, 在Rt△ABD中,sinB=,即AD=csinB, 在Rt△ADC中,sinC=,即AD=bsinC, ∴csinB=bsinC,即=, 同理可得=, 则==. 34.(2018•上海)如图,已知△ABC中,AB=BC=5,tan∠ABC=. (1)求边AC的长; (2)设边BC的垂直平分线与边AB的交点为D,求的值. 【分析】(1)过A作AE⊥BC,在直角三角形ABE中,利用锐角三角函数定义求出AC的长即可; (2)由DF垂直平分BC,求出BF的长,利用锐角三角函数定义求出DF的长,利用勾股定理求出BD的长,进而求出AD的长,即可求出所求. 【解答】解:(1)作A作AE⊥BC, 在Rt△ABE中,tan∠ABC==,AB=5, ∴AE=3,BE=4, ∴CE=BC﹣BE=5﹣4=1, 在Rt△AEC中,根据勾股定理得:AC==; (2)∵DF垂直平分BC, ∴BD=CD,BF=CF=, ∵tan∠DBF==, ∴DF=, 在Rt△BFD中,根据勾股定理得:BD==, ∴AD=5﹣=, 则=. 35.(2018•自贡)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长. 【分析】如图作CH⊥AB于H.在Rt△求出CH、BH,这种Rt△ACH中求出AH、AC即可解决问题; 【解答】解:如图作CH⊥AB于H. 在Rt△BCH中,∵BC=12,∠B=30°, ∴CH=BC=6,BH==6, 在Rt△ACH中,tanA==, ∴AH=8, ∴AC==10, ∴AB=AH+BH=8+6. 36.(2018•烟台)汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90) 【分析】先求得AC=PCtan∠APC=87、BC=PCtan∠BPC=21,据此得出AB=AC﹣BC=87﹣21=66,从而求得该车通过AB段的车速,比较大小即可得. 【解答】解:在Rt△APC中,AC=PCtan∠APC=30tan71°≈30×2.90=87, 在Rt△BPC中,BC=PCtan∠BPC=30tan35°≈30×0.70=21, 则AB=AC﹣BC=87﹣21=66, ∴该汽车的实际速度为=11m/s, 又∵40km/h≈11.1m/s, ∴该车没有超速. 37.(2018•绍兴)如图1,窗框和窗扇用“滑块铰链”连接,图3是图2中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂DE安装在窗扇上,交点A处装有滑块,滑块可以左右滑动,支点B,C,D始终在一直线上,延长DE交MN于点F.已知AC=DE=20cm,AE=CD=10cm,BD=40cm. (1)窗扇完全打开,张角∠CAB=85°,求此时窗扇与窗框的夹角∠DFB的度数; (2)窗扇部分打开,张角∠CAB=60°,求此时点A,B之间的距离(精确到0.1cm). (参考数据:≈1.732,≈2.449) 【分析】(1)根据平行四边形的判定和性质可以解答本题; (2)根据锐角三角函数和题意可以求得AB的长,从而可以解答本题. 【解答】解:(1)∵AC=DE=20cm,AE=CD=10cm, ∴四边形ACDE是平行四边形, ∴AC∥DE, ∴∠DFB=∠CAB, ∵∠CAB=85°, ∴∠DFB=85°; (2)作CG⊥AB于点G, ∵AC=20,∠CGA=90°,∠CAB=60°, ∴CG=,AG=10, ∵BD=40,CD=10, ∴CB=30, ∴BG==, ∴AB=AG+BG=10+10≈10+10×2.449=34.49≈34.5cm, 即A、B之间的距离为34.5cm. 38.(2018•临沂)如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2(+1)m.请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门? 【分析】过B作BD⊥AC于D,解直角三角形求出AD=xm,CD=BD=xm,得出方程,求出方程的解即可. 【解答】解: 工人师傅搬运此钢架能通过一个直径为2.1m的圆形门, 理由是:过B作BD⊥AC于D, ∵AB>BD,BC>BD,AC>AB, ∴求出DB长和2.1m比较即可, 设BD=xm, ∵∠A=30°,∠C=45°, ∴DC=BD=xm,AD=BD=xm, ∵AC=2(+1)m, ∴x+x=2(+1), ∴x=2, 即BD=2m<2.1m, ∴工人师傅搬运此钢架能通过一个直径为2.1m的圆形门. 39.(2018•长沙)为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山.汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°. (1)开通隧道前,汽车从A地到B地大约要走多少千米? (2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:≈141,≈1.73) 【分析】(1)过点C作AB的垂线CD,垂足为D,在直角△ACD中,解直角三角形求出CD,进而解答即可; (2)在直角△CBD中,解直角三角形求出BD,再求出AD,进而求出汽车从A地到B地比原来少走多少路程. 【解答】解:(1)过点C作AB的垂线CD,垂足为D, ∵AB⊥CD,sin30°=,BC=80千米, ∴CD=BC•sin30°=80×(千米), AC=(千米), AC+BC=80+40≈40×1.41+80=136.4(千米), 答:开通隧道前,汽车从A地到B地大约要走136.4千米; (2)∵cos30°=,BC=80(千米), ∴BD=BC•cos30°=80×(千米), ∵tan45°=,CD=40(千米), ∴AD=(千米), ∴AB=AD+BD=40+40≈40+40×1.73=109.2(千米), ∴汽车从A地到B地比原来少走多少路程为:AC+BC﹣AB=136.4﹣109.2=27.2 (千米). 答:汽车从A地到B地比原来少走的路程为27.2千米. 40.(2018•白银)随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4) 【分析】过点C作CD⊥AB于点D,利用锐角三角函数的定义求出CD及AD的长,进而可得出结论. 【解答】解:过点C作CD⊥AB于点D, 在Rt△ADC和Rt△BCD中, ∵∠CAB=30°,∠CBA=45°,AC=640, ∴CD=320,AD=320, ∴BD=CD=320,BC=320, ∴AC+BC=640+320≈1088, ∴AB=AD+BD=320+320≈864, ∴1088﹣864=224(公里), 答:隧道打通后与打通前相比,从A地到B地的路程将约缩短224公里. 41.(2018•随州)随州市新㵐水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3 日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD. (1)求最短的斜拉索DE的长; (2)求最长的斜拉索AC的长. 【分析】(1)根据等腰直角三角形的性质计算DE的长; (2)作AH⊥BC于H,如图2,由于BD=DE=3,则AB=3BD=15,在Rt△ABH中,根据等腰直角三角形的性质可计算出BH=AH=15,然后在Rt△ACH中利用含30度的直角三角形三边的关系即可得到AC的长. 【解答】解:(1)∵∠ABC=∠DEB=45°, ∴△BDE为等腰直角三角形, ∴DE=BE=×6=3. 答:最短的斜拉索DE的长为3m; (2)作AH⊥BC于H,如图2, ∵BD=DE=3, ∴AB=3BD=5×3=15, 在Rt△ABH中,∵∠B=45°, ∴BH=AH=AB=×15=15, 在Rt△ACH中,∵∠C=30°, ∴AC=2AH=30. 答:最长的斜拉索AC的长为30m. 42.(2018•遵义)如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05) (1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为 11.4 m. (2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计) 【分析】(1)根据直角三角形的性质和三角函数解答即可; (2)过点D作DH⊥地面于H,利用直角三角形的性质和三角函数解答即可. 【解答】解:(1)在Rt△ABC中, ∵∠BAC=64°,AC=5m, ∴AB=(m); 故答案为:11.4; (2)过点D作DH⊥地面于H,交水平线于点E, 在Rt△ADE中, ∵AD=20m,∠DAE=64°,EH=1.5m, ∴DE=sin64°×AD≈20×0.9≈18(m), 即DH=DE+EH=18+1.5=19.5(m), 答:如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是19.5m. 43.(2018•资阳)如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米. (1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度; (2)当她从点A跑动9米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D. 【分析】(1)在Rt△ACD中,由AD=可得答案; (2)设AF=x米,则BF=AB+AF=9+x,在Rt△BEF中求得AD=BE==18+x,由cos∠CAD=可建立关于x的方程,解之求得x的值,即可得出AD的长,继而根据CD=ADsin∠CAD求得CD从而得出答案. 【解答】解:(1)∵在Rt△ACD中,cos∠CAD=,AC=18、∠CAD=30°, ∴AD====12(米), 答:此时风筝线AD的长度为12米; (2)设AF=x米,则BF=AB+AF=9+x(米), 在Rt△BEF中,BE===18+x(米), 由题意知AD=BE=18+x(米), ∵CF=10, ∴AC=AF+CF=10+x, 由cos∠CAD=可得=, 解得:x=3+2, 则AD=18+(3+2)=24+3, ∴CD=ADsin∠CAD=(24+3)×=, 则C1D=CD+C1C=+=, 答:风筝原来的高度C1D为米. 44.(2018•山西)祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表. 项目 内容 课题 测量斜拉索顶端到桥面的距离 测量示意图 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. 测量数据 ∠A的度数 ∠B的度数 AB的长度 38° 28° 234米 … … (1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5) (2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可). 【分析】(1)过点C作CD⊥AB于点D.解直角三角形求出DC即可; (2)还需要补充的项目可为:测量工具,计算过程,人员分工,指导教师,活动感受等 【解答】解:(1)过点C作CD⊥AB于点D. 设CD=x米,在Rt△ADC中,∠ADC=90°,∠A=38°. ∵,∴. 在Rt△BDC中,∠BDC=90°,∠B=28°. ∵,∴. ∵AD+BD=AB=234,∴. 解得x=72. 答:斜拉索顶端点C到AB的距离为72米. (2)还需要补充的项目可为:测量工具,计算过程,人员分工,指导教师,活动感受等.(答案不唯一) 45.(2018•常德)图1是一商场的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转37°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据:sin37°≈0.6,cos37°≈0.8,≈1.4) 【分析】作BE⊥AD于点E,作CF⊥AD于点F,延长FC到点M,使得BE=CM,则EM=BC,在Rt△ABE、Rt△CDF中可求出AE、BE、DF、FC的长度,进而可得出EF的长度,再在Rt△MEF中利用勾股定理即可求出EM的长,此题得解. 【解答】解:作BE⊥AD于点E,作CF⊥AD于点F,延长FC到点M,使得BE=CM,如图所示. ∵AB=CD,AB+CD=AD=2, ∴AB=CD=1. 在Rt△ABE中,AB=1,∠A=37°, ∴BE=AB•sin∠A≈0.6,AE=AB•cos∠A≈0.8. 在Rt△CDF中,CD=1,∠D=45°, ∴CF=CD•sin∠D≈0.7,DF=CD•cos∠D≈0.7. ∵BE⊥AD,CF⊥AD, ∴BE∥CM, 又∵BE=CM, ∴四边形BEMC为平行四边形, ∴BC=EM,CM=BE. 在Rt△MEF中,EF=AD﹣AE﹣DF=0.5,FM=CF+CM=1.3, ∴EM=≈1.4, ∴B与C之间的距离约为1.4米. 46.(2018•台州)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53) 【分析】作CE⊥BD于F,AF⊥CE于F,如图2,易得四边形AHEF为矩形,则EF=AH=3.4m,∠HAF=90°,再计算出∠CAF=28°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF即可. 【解答】解:作CE⊥BD于F,AF⊥CE于F,如图2, 易得四边形AHEF为矩形, ∴EF=AH=3.4m,∠HAF=90°, ∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°, 在Rt△ACF中,∵sin∠CAF=, ∴CF=9sin28°=9×0.47=4.23, ∴CE=CF+EF=4.23+3.4≈7.6(m), 答:操作平台C离地面的高度为7.6m. 47.(2018•岳阳)图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°. (1)求点M到地面的距离; (2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:≈1.73,结果精确到0.01米) 【分析】(1)构建直角△OMN,求ON的长,相加可得BN的长,即点M到地面的距离; (2)左边根据要求留0.65米的安全距离,即取CE=0.65,车宽EH=2.55,计算高GH的长即可,与3.5作比较,可得结论. 【解答】解:(1)如图,过M作MN⊥AB于N,交BA的延长线于N, Rt△OMN中,∠NOM=60°,OM=1.2, ∴∠M=30°, ∴ON=OM=0.6, ∴NB=ON+OB=3.3+0.6=3.9; 即点M到地面的距离是3.9米; (2)取CE=0.65,EH=2.55, ∴HB=3.9﹣2.55﹣0.65=0.7, 过H作GH⊥BC,交OM于G,过O作OP⊥GH于P, ∵∠GOP=30°, ∴tan30°==, ∴GP=OP=≈0.404, ∴GH=3.3+0.404=3.704≈3.70>3.5, ∴货车能安全通过. 48.(2018•徐州)如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)参考数据:≈1.414,≈1.732 【分析】利用锐角三角函数,在Rt△CDE中计算出坝高DE及CE的长,通过矩形ADEF.利用等腰直角三角形的边角关系,求出BF的长,得到坝底的宽. 【解答】解:在Rt△CDE中, ∵sin∠C=,cos∠C= ∴DE=sin30°×DC=×14=7(m), CE=cos30°×DC=×14=7≈12.124≈12.12, ∵四边形AFED是矩形, ∴EF=AD=6m,AF=DE=7m 在Rt△ABF中, ∵∠B=45° ∴DE=AF=7m, ∴BC=BF+EF+EC≈7+6+12.12=25.12≈25.1(m) 答:该坝的坝高和坝底宽分别为7m和25.1m. 49.(2018•河南)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答. 如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850) 【分析】利用锐角三角函数,在Rt△ACE和Rt△DBF中,分别求出AE、BF 的长.计算出EF.通过矩形CEFH得到CH的长. 【解答】解:在Rt△ACE中, ∵tan∠CAE=, ∴AE==≈≈21(cm) 在Rt△DBF中, ∵tan∠DBF=, ∴BF==≈=40(cm) ∵EF=EA+AB+BF≈21+90+40=151(cm) ∵CE⊥EF,CH⊥DF,DF⊥EF ∴四边形CEFH是矩形, ∴CH=EF=151cm 答:高、低杠间的水平距离CH的长为151cm. 50.(2018•嘉兴)如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°,当点P位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳. (1)上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m) (2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41,≈1.73) 【分析】(1)只要证明△CFP1是等腰直角三角形,即可解决问题; (2)解直角三角形求出CP2的长即可解决问题; 【解答】解:(1)如图2中,当P位于初始位置时,CP0=2m, 如图3中,上午10:00时,太阳光线与地面的夹角为65°,上调的距离为P0P1. ∵∠1=90°,∠CAB=90°,∠ABE=65°, ∴∠AP1E=115°, ∴∠CP1E=65°, ∵∠DP1E=20°, ∴∠CP1F=45°, ∵CF=P1F=1m, ∴∠C=∠CP1F=45°, ∴△CP1F是等腰直角三角形, ∴P1C=m, ∴P0P1=CP0﹣P1C=2﹣≈0.6m, 即为使遮阳效果最佳,点P需从P0上调0.6m. (2)如图4中,中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P调到P2处. ∵P2E∥AB, ∴∠CP2E=∠CAB=90°, ∵∠DP2E=20°, ∴∠CP2F=70°,作FG⊥AC于G,则CP2=2CG=1×cos70°≈0.68m, ∴P1P2=CP1﹣CP2=﹣0.68≈0.7m, 即点P在(1)的基础上还需上调0.7m. 查看更多