中考数学常见几何模型简介

中考数学常见几何模型简介

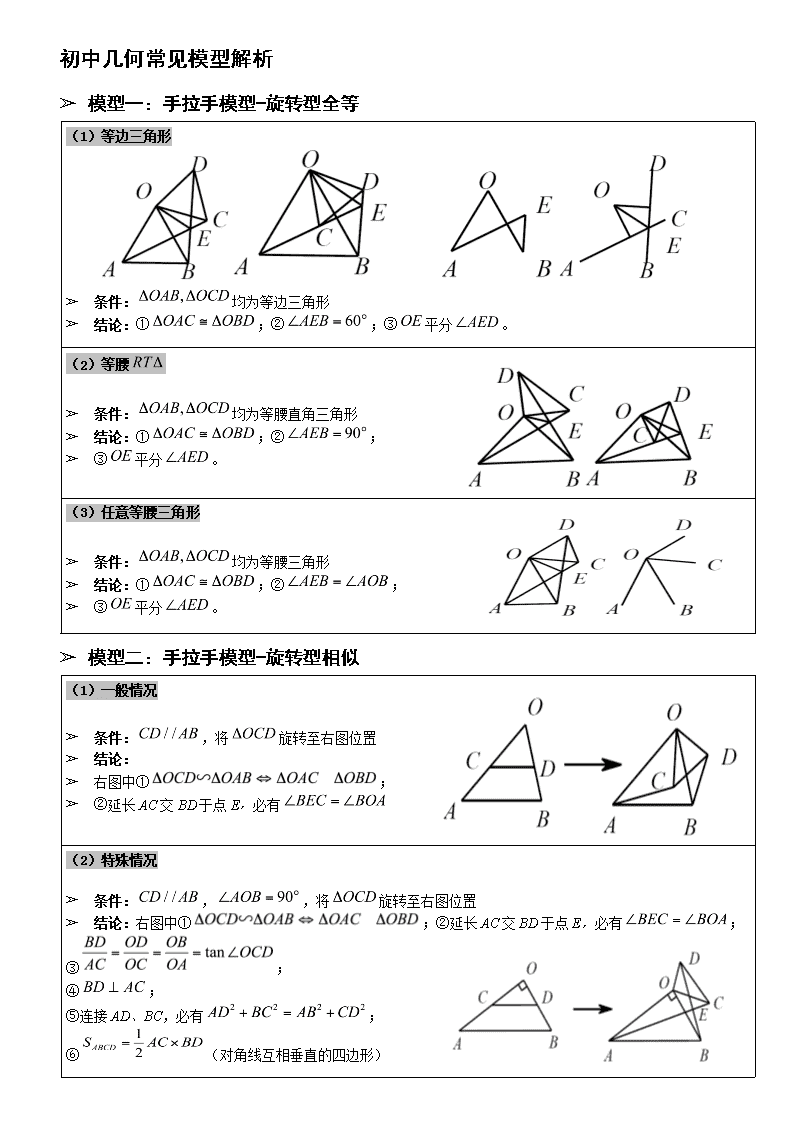
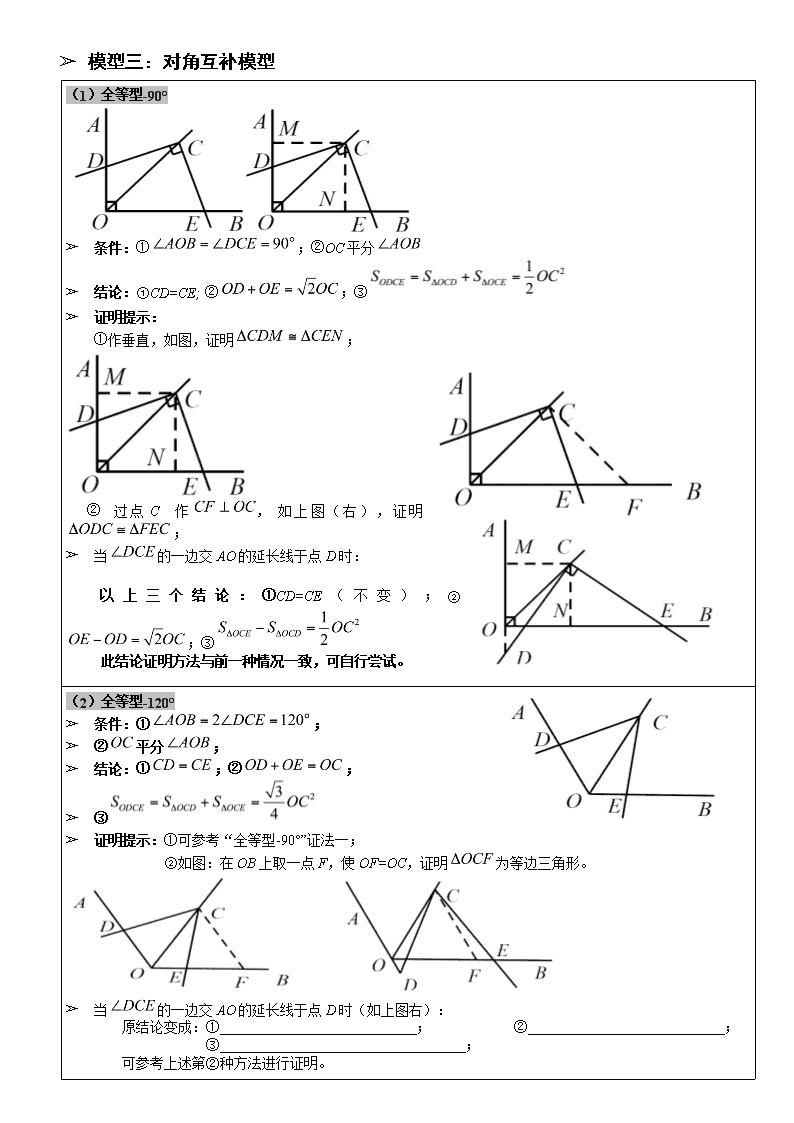
初中几何常见模型解析 ➢ 模型一：手拉手模型-旋转型全等 ‎（1）等边三角形 ‎ ‎ ➢ 条件：均为等边三角形 ➢ 结论：①；②；③平分。‎ ‎（2）等腰 ‎ ‎ ➢ 条件：均为等腰直角三角形 ➢ 结论：①；②；‎ ➢ ‎③平分。‎ ‎（3）任意等腰三角形 ➢ 条件：均为等腰三角形 ➢ 结论：①；②；‎ ➢ ‎③平分。‎ ➢ 模型二：手拉手模型-旋转型相似 ‎（1）一般情况 ➢ 条件：，将旋转至右图位置 ➢ 结论：‎ ➢ 右图中①；‎ ➢ ‎②延长AC交BD于点E，必有 ‎（2）特殊情况 ➢ 条件：，，将旋转至右图位置 ➢ 结论：右图中①；②延长AC交BD于点E，必有；‎ ‎③；‎ ‎④；‎ ‎⑤连接AD、BC，必有；‎ ‎⑥（对角线互相垂直的四边形）‎ ➢ 模型三：对角互补模型 ‎（1）全等型-90°‎ ➢ 条件：①；②OC平分 ➢ 结论：①CD=CE; ②；③‎ ➢ 证明提示：‎ ‎①作垂直，如图，证明；‎ ‎ ‎ ‎②过点C作,如上图（右），证明；‎ ➢ 当的一边交AO的延长线于点D时：‎ 以上三个结论：①CD=CE（不变）；②；③‎ ‎ 此结论证明方法与前一种情况一致，可自行尝试。‎ ‎（2）全等型-120°‎ ➢ 条件：①；‎ ➢ ‎②平分；‎ ➢ 结论：①；②；‎ ➢ ‎③‎ ➢ 证明提示：①可参考“全等型-90°”证法一；‎ ‎②如图：在OB上取一点F，使OF=OC，证明为等边三角形。‎ ‎ ‎ ➢ 当的一边交AO的延长线于点D时（如上图右）：‎ 原结论变成：① ； ② ；‎ ‎ ③ ；‎ 可参考上述第②种方法进行证明。‎ ‎（3）全等型-任意角 ➢ 条件：①；②；‎ ➢ 结论：①平分；②；‎ ➢ ‎③.‎ ➢ 当的一边交AO的延长线于点D时（如右上图）：‎ 原结论变成：① ； ② ；‎ ‎ ③ ；‎ 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。‎ 如图所示，若将条件“平分”去掉，条件①不变，平分，结论变化如下：‎ 结论：①；②；‎ ‎③.‎ ‎ ‎ ➢ 对角互补模型总结：‎ ‎①常见初始条件：四边形对角互补；‎ ‎ 注意两点：四点共圆及直角三角形斜边中线；‎ ‎②初始条件“角平分线”与“两边相等”的区别；‎ ‎③两种常见的辅助线作法；‎ ‎④注意下图中平分时 ‎，相等是如何推导的？‎ ➢ 模型四：角含半角模型90°‎ ‎（1）角含半角模型90°-1‎ ➢ 条件：①正方形；②；‎ ➢ 结论：①；②的周长为正方形周长的一半；‎ 也可以这样：‎ ➢ 条件：①正方形；②‎ ➢ 结论：‎ ‎（2）角含半角模型90°-2‎ ➢ 条件：①正方形；②；‎ ➢ 结论：‎ ➢ 辅助线如下图所示：‎ ‎（3）角含半角模型90°-3‎ ➢ 条件：①；②；‎ ➢ 结论：‎ 若旋转到外部时，结论仍然成立。‎ ‎（4）角含半角模型90°变形 ‎ ‎ ➢ 条件：①正方形；②；‎ ➢ 结论：为等腰直角三角形。‎ ➢ ➢ 模型五：倍长中线类模型 ‎（1）倍长中线类模型-1‎ ➢ 条件：①矩形；②;③；‎ ➢ 结论：‎ 模型提取：①有平行线；②平行线间线段有中点；‎ ‎ 可以构造“8”字全等。‎ ‎（2）倍长中线类模型-2‎ ➢ 条件：①平行四边形；②；③；④.‎ ➢ 结论：‎ ➢ ➢ 模型六：相似三角形360°旋转模型 ‎（1）相似三角形（等腰直角）360°旋转模型-倍长中线法 ‎ ‎ ➢ 条件：①、均为等腰直角三角形；②‎ ➢ 结论：①；②‎ ‎（1）相似三角形（等腰直角）360°旋转模型-补全法 ‎ ‎ ➢ 条件：①、均为等腰直角三角形；②；‎ ➢ 结论：①；②‎ ‎（2）任意相似直角三角形360°旋转模型-补全法 ‎ ‎ ➢ 条件：①；②;③。‎ ➢ 结论：①；②‎ ‎（2）任意相似直角三角形360°旋转模型-倍长法 ➢ 条件：①；②;③。‎ ➢ 结论：①；②‎ ➢ ➢ 模型七：最短路程模型 ‎（1）最短路程模型一（将军饮马类）‎ ‎（2）最短路程模型二（点到直线类1）‎ ‎ ‎ ➢ 条件：①平分；②为上一定点；③为上一动点；④为上一动点；‎ ➢ 求：最小时，的位置？‎ ‎（3）最短路程模型二（点到直线类2）‎ ‎ ‎ ‎（4）最短路程模型二（点到直线类3）‎ ➢ 条件：‎ ➢ 问题：为何值时，最小 ➢ 求解方法：①轴上取，使；②过作，交轴于点，即为所求；‎ ‎ ③，即.‎ ‎（5）最短路程模型三（旋转类最值模型）‎ ‎ ‎ ‎（6）最短路程模型三（动点在圆上）‎ ‎ ‎ ➢ ➢ 模型八：二倍角模型 ➢ 模型九：相似三角形模型 ‎（1）相似三角形模型-基本型 （2）相似三角形模型-斜交型 ‎（3）相似三角形模型-一线三角型 （4）相似三角形模型-圆幂定理型