初中数学突破中考压轴题几何模型之正方形的半角模型

初中数学突破中考压轴题几何模型之正方形的半角模型

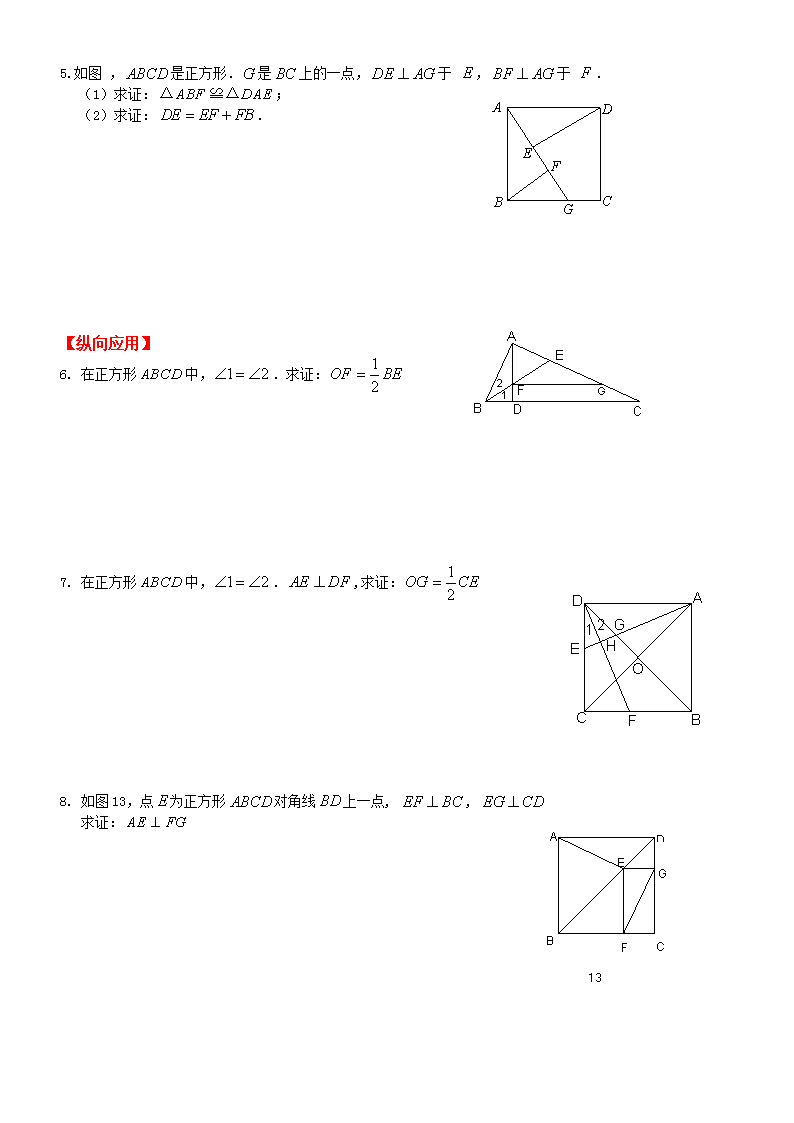
‎ 正方形角含半角模型提升 例1．如图，折叠正方形纸片，先折出折痕，再折叠使边与对角线重合，得折痕，使，求．‎ 例2 ．如图，为正方形内一点，，并且点到边的距离也等于，求正方形的面积？‎ 例3. 如图，、分别为正方形的边、上的一点，，垂足为，，则有，为什么？‎ 例4. 如图，在正方形的、边上取、两点，使，于. 求证： ‎ 例5.(1) 如图1,在正方形中,点,分别在边,上,,交于点,.‎ 求证：.‎ 图2‎ ‎(2) 如图2,在正方形中,点,,,分别在边,,,上,,交于点,,.求的长.‎ ‎【双基训练】‎ ‎1. 如图6，点在线段上，四边形与都是正方形，其边长分别为和，则的面积为________．‎ ‎ ‎ ‎ (6) (7)‎ ‎2．你可以依次剪6张正方形纸片，拼成如图7所示图形．如果你所拼得的图形中正方形①的面积为1，且正方形⑥与正方形③的面积相等，那么正方形⑤的面积为________．‎ ‎3.如图9，已知正方形的面积为35平方厘米，、分别为边、上的点．、相交于，并且的面积为14平方厘米，的面积为5平方厘米，那么四边形的面积是________．‎ ‎4. 如图，、、三点在同一条直线上，。分别以 ‎、为边作正方形和正方形，连接，‎ ‎。‎ ‎ 求证：。‎ ‎5.如图 ，是正方形．是上的一点，于 ，于 ． ‎ ‎（1）求证：； ‎A D E F C G B ‎（2）求证：．‎ ‎【纵向应用】‎ ‎6. 在正方形中，．求证：‎ ‎7. 在正方形中，．,求证： ‎ ‎8. 如图13，点为正方形对角线上一点, , ‎ A D ‎ 求证：‎ B C F ‎ 13‎ E ‎ ‎ G ‎9.已知：点、分别正方形中和的中点，连接和相交于点,‎ 于点.‎ ‎（1）求证： ；‎ ‎（2）如果,求的长；‎ ‎（3）求证： ‎ ‎ ‎ 例1. 已知：如图，是正方形内点，．‎ A P C D B ‎ 求证：是正三角形．‎ P C G F B Q A D E 例2. 如图，分别以的和为一边，在的外侧作正方形和正方形，点是的中点．‎ 求证：点到边的距离等于的一半．‎ 例4. 如图，四边形为正方形，，，与相交于．‎ 求证：．‎ ‎ A F D E C B ‎ 例6. 设是正方形一边上的任一点，，平分．‎ 求证：．‎ D F E P C B A D A C B P D 例7. 已知：是边长为1的正方形内的一点，求的最小值．‎ 例8. 为正方形内的一点，并且，，，求正方形的边长．‎ A C B P D ‎【双基训练】‎ ‎1.如图，四边形是正方形，对角线、相交于，四边形是菱形，若正方形的边长为6，则菱形的面积为________．‎ ‎2.如图，是正方形，为上一点，四边形恰是一个菱形，则=________．‎ ‎【纵向应用】‎ ‎3.如图，四边形是边长为的正方形，点，分别是边，的中点，，且交正方形外角的平分线于点．‎ ‎ （1）证明：；‎ ‎（2）证明：；‎ ‎（3）求的面积．‎ ‎【横向拓展】‎ ‎4.如图，四边形是正方形，是等边三角形，为对角线（不含点）上任意一点，将绕点逆时针旋转得到，连接、、.‎ ‎⑴ 求证：；‎ ‎⑵ ①当点在何处时，的值最小；‎ ‎②当点在何处时，的值最小，并说明理由；‎ ‎⑶ 当的最小值为时，求正方形的边长.‎ E A D B C N M