中考数学复习专题四几何变换压轴题试题含答案

中考数学复习专题四几何变换压轴题试题含答案

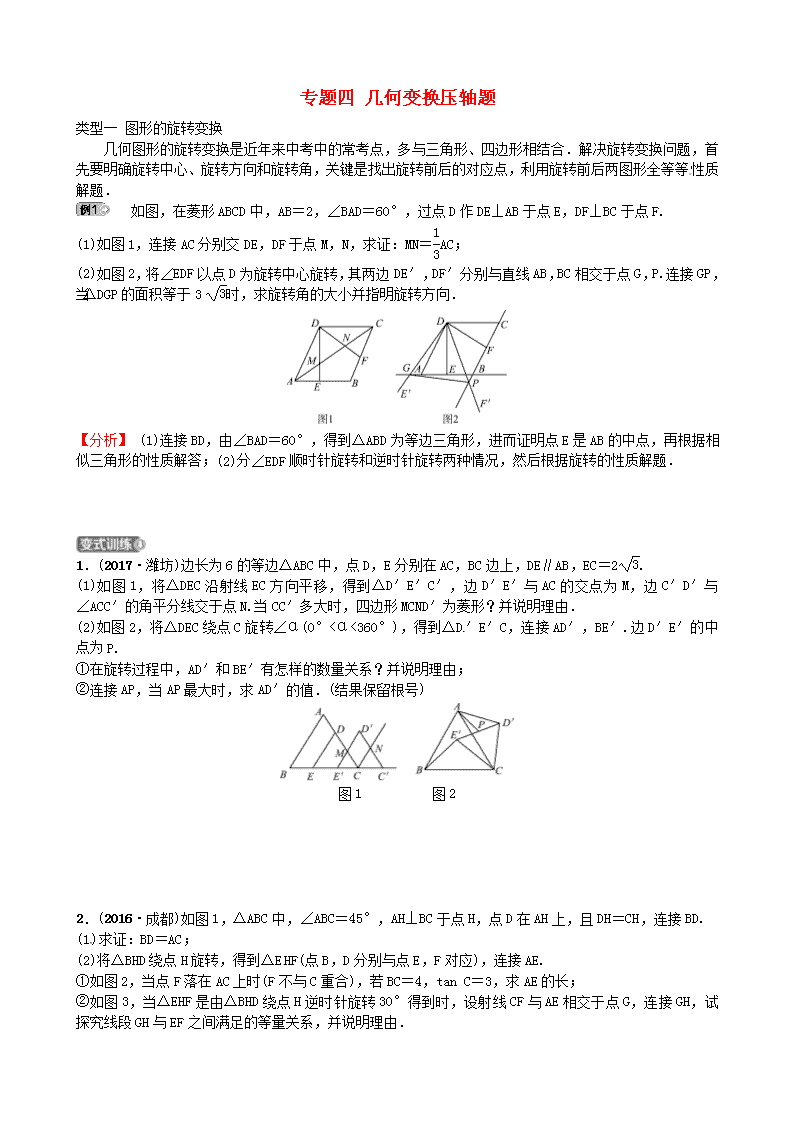
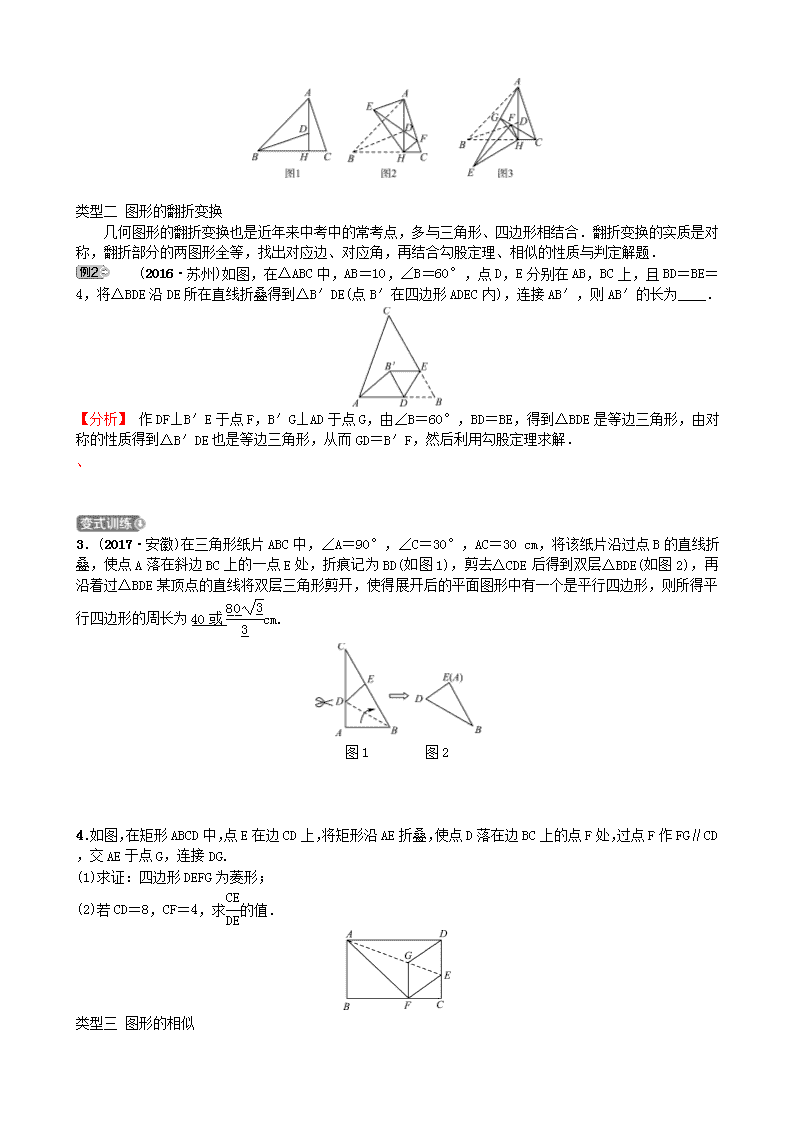
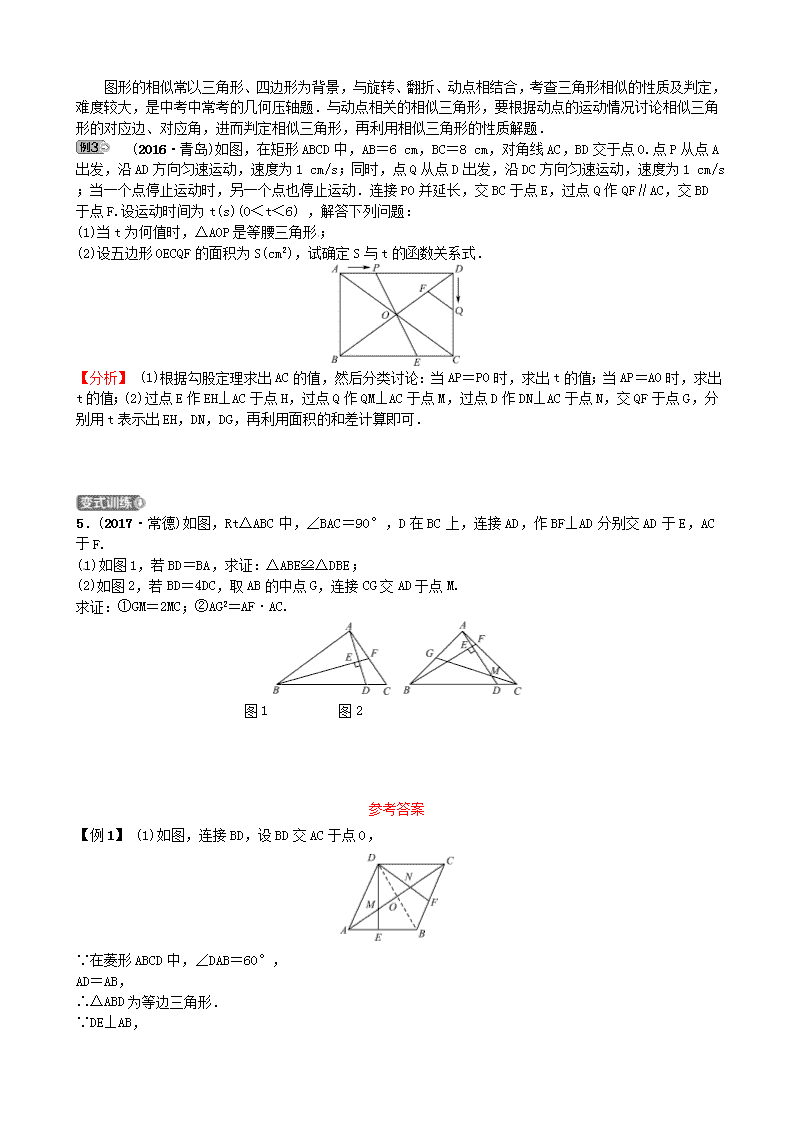
专题四 几何变换压轴题 类型一 图形的旋转变换 ‎ 几何图形的旋转变换是近年来中考中的常考点，多与三角形、四边形相结合．解决旋转变换问题，首先要明确旋转中心、旋转方向和旋转角，关键是找出旋转前后的对应点，利用旋转前后两图形全等等性质解题．‎ ‎ 如图，在菱形ABCD中，AB＝2，∠BAD＝60°，过点D作DE⊥AB于点E，DF⊥BC于点F.‎ ‎(1)如图1，连接AC分别交DE，DF于点M，N，求证：MN＝AC；‎ ‎(2)如图2，将∠EDF以点D为旋转中心旋转，其两边DE′，DF′分别与直线AB，BC相交于点G，P.连接GP，当△DGP的面积等于3时，求旋转角的大小并指明旋转方向．‎ ‎ ‎ ‎【分析】 (1)连接BD，由∠BAD＝60°，得到△ABD为等边三角形，进而证明点E是AB的中点，再根据相似三角形的性质解答；(2)分∠EDF顺时针旋转和逆时针旋转两种情况，然后根据旋转的性质解题．‎ ‎ ‎ ‎1．(2017·潍坊)边长为6的等边△ABC中，点D，E分别在AC，BC边上，DE∥AB，EC＝2.‎ ‎(1)如图1，将△DEC沿射线EC方向平移，得到△D′E′C′，边D′E′与AC的交点为M，边C′D′与∠ACC′的角平分线交于点N.当CC′多大时，四边形MCND′为菱形？并说明理由．‎ ‎(2)如图2，将△DEC绕点C旋转∠α(0°<α<360°)，得到△D′E′C，连接AD′，BE′.边D′E′的中点为P.‎ ‎①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；‎ ‎②连接AP，当AP最大时，求AD′的值．(结果保留根号)‎ ‎ 　　　　‎ 图1　　　　　图2‎ ‎2．(2016·成都)如图1，△ABC中，∠ABC＝45°，AH⊥BC于点H，点D在AH上，且DH＝CH，连接BD.‎ ‎(1)求证：BD＝AC；‎ ‎(2)将△BHD绕点H旋转，得到△EHF(点B，D分别与点E，F对应)，连接AE.‎ ‎①如图2，当点F落在AC上时(F不与C重合)，若BC＝4，tan C＝3，求AE的长；‎ ‎②如图3，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的等量关系，并说明理由．‎ ‎ ‎ 类型二 图形的翻折变换 ‎ 几何图形的翻折变换也是近年来中考中的常考点，多与三角形、四边形相结合．翻折变换的实质是对称，翻折部分的两图形全等，找出对应边、对应角，再结合勾股定理、相似的性质与判定解题．‎ ‎ (2016·苏州)如图，在△ABC中，AB＝10，∠B＝60°，点D，E分别在AB，BC上，且BD＝BE＝4，将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内)，连接AB′，则AB′的长为____．‎ ‎ ‎ ‎【分析】 作DF⊥B′E于点F，B′G⊥AD于点G，由∠B＝60°，BD＝BE，得到△BDE是等边三角形，由对称的性质得到△B′DE也是等边三角形，从而GD＝B′F，然后利用勾股定理求解．‎ ‎、‎ ‎ ‎ ‎3．(2017·安徽)在三角形纸片ABC中，∠A＝90°，∠C＝30°，AC＝‎30 cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD(如图1)，剪去△CDE后得到双层△BDE(如图2)，再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为40或cm.‎ ‎ ‎ 图1　　　　图2‎ ‎4．如图，在矩形ABCD中，点E在边CD上，将矩形沿AE折叠，使点D落在边BC上的点F处，过点F作FG∥CD，交AE于点G，连接DG.‎ ‎(1)求证：四边形DEFG为菱形；‎ ‎(2)若CD＝8，CF＝4，求的值．‎ ‎ ‎ 类型三 图形的相似 ‎ 图形的相似常以三角形、四边形为背景，与旋转、翻折、动点相结合，考查三角形相似的性质及判定，难度较大，是中考中常考的几何压轴题．与动点相关的相似三角形，要根据动点的运动情况讨论相似三角形的对应边、对应角，进而判定相似三角形，再利用相似三角形的性质解题．‎ ‎ (2016·青岛)如图，在矩形ABCD中，AB＝‎6 cm，BC＝‎8 cm，对角线AC，BD交于点O.点P从点A出发，沿AD方向匀速运动，速度为‎1 cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为‎1 cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F.设运动时间为t(s)(0＜t＜6) ，解答下列问题：‎ ‎(1)当t为何值时，△AOP是等腰三角形；‎ ‎(2)设五边形OECQF的面积为S(cm2)，试确定S与t的函数关系式．‎ ‎ ‎ ‎【分析】 (1)根据勾股定理求出AC的值，然后分类讨论：当AP＝PO时，求出t的值；当AP＝AO时，求出t的值；(2)过点E作EH⊥AC于点H，过点Q作QM⊥AC于点M，过点D作DN⊥AC于点N，交QF于点G，分别用t表示出EH，DN，DG，再利用面积的和差计算即可．‎ ‎ ‎ ‎5．(2017·常德)如图，Rt△ABC中，∠BAC＝90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F.‎ ‎(1)如图1，若BD＝BA，求证：△ABE≌△DBE；‎ ‎(2)如图2，若BD＝4DC，取AB的中点G，连接CG交AD于点M.‎ 求证：①GM＝2MC；②AG2＝AF·AC.‎ ‎ 　　　　‎ 图1　　　　　图2‎ 参考答案 ‎【例1】 (1)如图，连接BD，设BD交AC于点O，‎ ‎∵在菱形ABCD中，∠DAB＝60°，‎ AD＝AB，‎ ‎∴△ABD为等边三角形．‎ ‎∵DE⊥AB，‎ ‎∴点E为AB的中点．‎ ‎∵AE∥CD，‎ ‎∴＝＝.‎ 同理＝.‎ ‎∴M，N是线段AC的三等分点，∴MN＝AC.‎ ‎(2)∵AB∥CD，∠BAD＝60°，∴∠ADC＝120°.‎ ‎∵∠ADE＝∠CDF＝30°，∴∠EDF＝60°.‎ 当∠EDF顺时针旋转时，由旋转的性质知，‎ ‎∠EDG＝∠FDP，∠GDP＝∠EDF＝60°.‎ ‎∵DE＝DF＝，∠DEG＝∠DFP＝90°，‎ ‎∴△DEG≌△DFP，‎ ‎∴DG＝DP，∴△DGP是等边三角形．‎ 则S△DGP＝DG2.由DG2＝3，‎ 又∵DG＞0，解得DG＝2.‎ ‎∴cos∠EDG＝＝＝，∴∠EDG＝60°.‎ ‎∴当顺时针旋转60°时，△DGP的面积是3.‎ 同理，当逆时针旋转60°时，△DGP的面积也是3.‎ 综上所述，当∠EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积是3.‎ ‎【变式训练】 ‎ ‎1．解：(1)当CC′＝时，四边形MCND′为菱形．‎ 理由：由平移的性质得CD∥C′D′，DE∥D′E′.‎ ‎∵△ABC为等边三角形，∴∠B＝∠ACB＝60°，‎ ‎∴∠ACC′＝180°－60°＝120°.‎ ‎∵CN是∠ACC′的角平分线，∴∠NCC′＝60°.‎ ‎∵AB∥DE，DE∥D′E′，∴AB∥D′E′，‎ ‎∴∠D′E′C′＝∠B＝60°，‎ ‎∴∠D′E′C′＝∠NCC′，∴D′E′∥CN.‎ ‎∴四边形MCND′为平行四边形．‎ ‎∵∠ME′C′＝∠MCE′＝60°，∠NCC′＝∠NC′C＝60°，‎ ‎∴△MCE′和△NCC′为等边三角形，‎ 故MC＝CE′，NC＝CC′.‎ 又E′C′＝2，CC′＝，∴CE′＝CC′＝，‎ ‎∴MC＝CN，∴四边形MCND′为菱形．‎ ‎(2)①AD′＝BE′.‎ 理由：当α≠180°时，由旋转的性质得∠ACD′＝∠BCE′.‎ 由(1)知AC＝BC，CD′＝CE′，‎ ‎∴△ACD′≌△BCE′，∴AD′＝BE′.‎ 当α＝180°时，AD′＝AC＋CD′，BE′＝BC＋CE′，‎ 即AD′＝BE′.‎ 综上可知，AD′＝BE′.‎ ‎②连接CP，在△ACP中，由三角形三边关系得，AP

查看更多