2013中考数学试题分类汇编平移旋转翻折

2013中考数学试题分类汇编平移旋转翻折

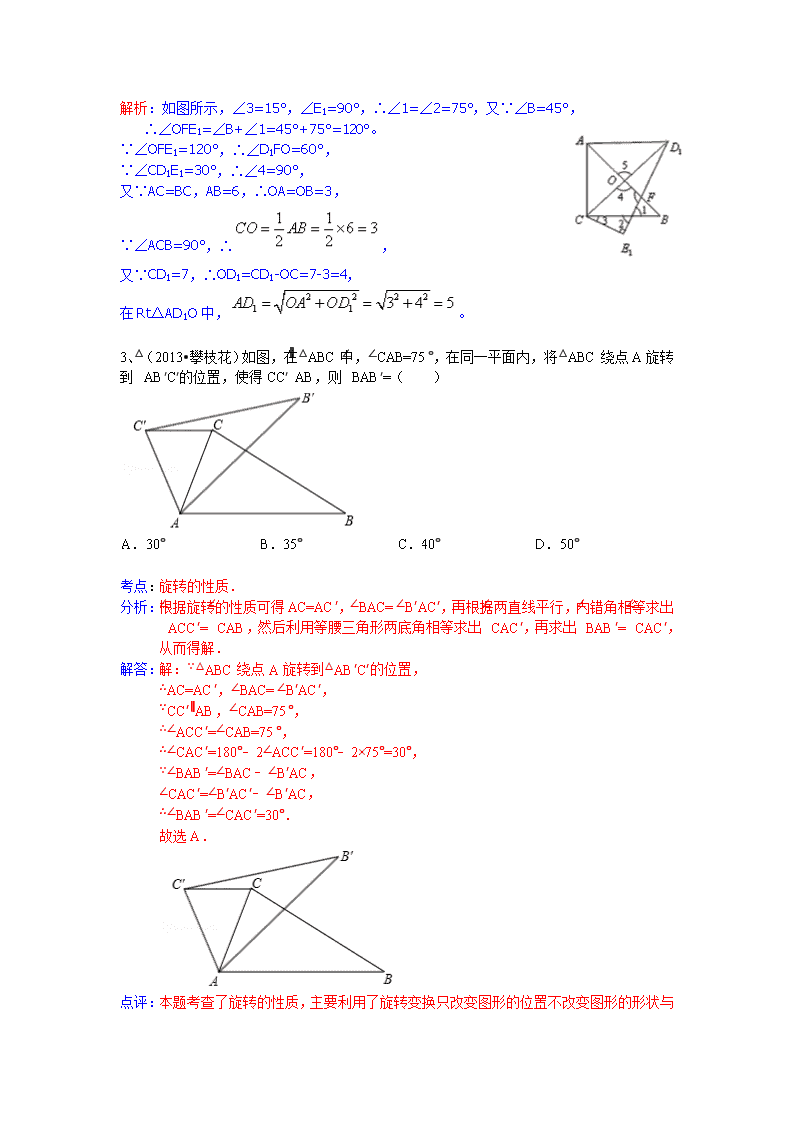
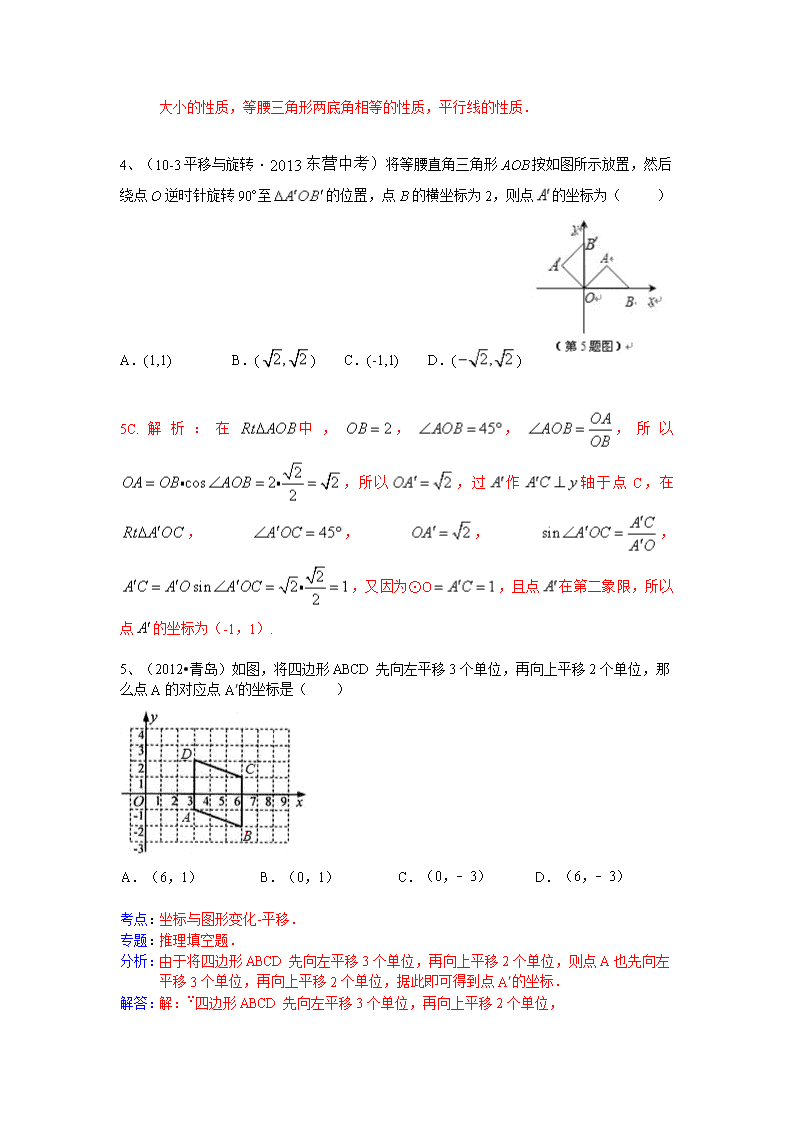
‎2013中考全国100份试卷分类汇编 全等变换（平移、旋转、翻折）‎ ‎1、（2013•天津）如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是（　　）‎ ‎　‎ A．‎ 矩形 B．‎ 菱形 C．‎ 正方形 D．‎ 梯形 考点：‎ 旋转的性质；矩形的判定．3718684‎ 分析：‎ 根据旋转的性质可得AE=CE，DE=EF，再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形，然后利用等腰三角形三线合一的性质求出∠ADC=90°，再利用有一个角是直角的平行四边形是矩形解答．‎ 解答：‎ 解：∵△ADE绕点E旋转180°得△CFE，‎ ‎∴AE=CE，DE=EF，‎ ‎∴四边形ADCF是平行四边形，‎ ‎∵AC=BC，点D是边AB的中点，‎ ‎∴∠ADC=90°，‎ ‎∴四边形ADCF矩形．‎ 故选A．‎ 点评：‎ 本题考查了旋转的性质，矩形的判定，主要利用了对角线互相平分的四边形是平行四边形，有一个角是直角是平行四边形是矩形的判定方法，熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．‎ D C A E B A D1‎ O E1‎ B C 图甲 图乙 ‎2、(2013年黄石)把一副三角板如图甲放置，其中，，，斜边，，把三角板绕着点顺时针旋转得到△（如图乙），此时与交于点，则线段的长度为 A. B. ‎ C. 4 D.‎ 答案：B 解析：如图所示，∠3=15°，∠E1=90°，∴∠1=∠2=75°，又∵∠B=45°， ∴∠OFE1=∠B+∠1=45°+75°=120°。‎ ‎∵∠OFE1=120°，∴∠D1FO=60°， ∵∠CD1E1=30°，∴∠4=90°， 又∵AC=BC，AB=6，∴OA=OB=3， ∵∠ACB=90°，∴， 又∵CD1=7，∴OD1=CD1-OC=7-3=4， 在Rt△AD1O中，。‎ ‎3、（2013•攀枝花）如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（　　）‎ ‎　‎ A．‎ ‎30°‎ B．‎ ‎35°‎ C．‎ ‎40°‎ D．‎ ‎50°‎ 考点：‎ 旋转的性质．‎ 分析：‎ 根据旋转的性质可得AC=AC′，∠BAC=∠B′AC′，再根据两直线平行，内错角相等求出∠ACC′=∠CAB，然后利用等腰三角形两底角相等求出∠CAC′，再求出∠BAB′=∠CAC′，从而得解．‎ 解答：‎ 解：∵△ABC绕点A旋转到△AB′C′的位置，‎ ‎∴AC=AC′，∠BAC=∠B′AC′，‎ ‎∵CC′∥AB，∠CAB=75°，‎ ‎∴∠ACC′=∠CAB=75°，‎ ‎∴∠CAC′=180°﹣2∠ACC′=180°﹣2×75°=30°，‎ ‎∵∠BAB′=∠BAC﹣∠B′AC，‎ ‎∠CAC′=∠B′AC′﹣∠B′AC，‎ ‎∴∠BAB′=∠CAC′=30°．‎ 故选A．‎ 点评：‎ 本题考查了旋转的性质，主要利用了旋转变换只改变图形的位置不改变图形的形状与大小的性质，等腰三角形两底角相等的性质，平行线的性质．‎ ‎4、（10-3平移与旋转·2013东营中考）将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至的位置，点B的横坐标为2，则点的坐标为（ ）‎ A．(1,1) B．() C．(-1,1) D．()‎ ‎5C.解析：在中，，，，所以，所以，过作轴于点C，在，，，，，又因为⊙O，且点在第二象限，所以点的坐标为（-1，1）.‎ ‎5、（2012•青岛）如图，将四边形ABCD先向左平移3个单位，再向上平移2个单位，那么点A的对应点A′的坐标是（　　）‎ ‎　‎ A．‎ ‎（6，1）‎ B．‎ ‎（0，1）‎ C．‎ ‎（0，﹣3）‎ D．‎ ‎（6，﹣3）‎ 考点：‎ 坐标与图形变化-平移．‎ 专题：‎ 推理填空题．‎ 分析：‎ 由于将四边形ABCD先向左平移3个单位，再向上平移2个单位，则点A也先向左平移3个单位，再向上平移2个单位，据此即可得到点A′的坐标．‎ 解答：‎ 解：∵四边形ABCD先向左平移3个单位，再向上平移2个单位，‎ ‎∴点A也先向左平移3个单位，再向上平移2个单位，‎ ‎∴由图可知，A′坐标为（0，1）．‎ 故选B．‎ 点评：‎ 本题考查了坐标与图形的变化﹣﹣平移，本题本题考查了坐标系中点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．‎ ‎6、（2013泰安）在如图所示的单位正方形网格中，△ABC经过平移后得到△A1B‎1C1，已知在AC上一点P（2.4，2）平移后的对应点为P1，点P1绕点O逆时针旋转180°，得到对应点P2，则P2点的坐标为（　　）‎ ‎　 A．（1.4，﹣1） B．（1.5，2） C．（1.6，1） D．（2.4，1）‎ 考点：坐标与图形变化-旋转；坐标与图形变化-平移．‎ 分析：根据平移的性质得出，△ABC的平移方向以及平移距离，即可得出P1坐标，进而利用中心对称图形的性质得出P2点的坐标．‎ 解答：解：∵A点坐标为：（2，4），A1（﹣2，1），‎ ‎∴点P（2.4，2）平移后的对应点P1为：（﹣1.6，﹣1），‎ ‎∵点P1绕点O逆时针旋转180°，得到对应点P2，‎ ‎∴P2点的坐标为：（1.6，1）．‎ 故选：C．‎ 点评：此题主要考查了旋转的性质以及平移的性质，根据已知得出平移距离是解题关键．‎ ‎7、（2013•湖州）如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则的值为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 矩形的性质；翻折变换（折叠问题）．‎ 分析：‎ 根据翻折的性质可得∠BAC=∠EAC，再根据矩形的对边平行可得AB∥CD，根据两直线平行，内错角相等可得∠DAC=∠BAC，从而得到∠EAC=∠DAC，设AE与CD相交于F，根据等角对等边的性质可得AF=CF，再求出DF=EF，从而得到△ACF和△EDF相似，根据相似三角形对应边成比例求出=，设DF=3x，FC=5x，在Rt△ADF中，利用勾股定理列式求出AD，再根据矩形的对边相等求出AB，然后代入进行计算即可得解．‎ 解答：‎ 解：∵矩形沿直线AC折叠，点B落在点E处，‎ ‎∴∠BAC=∠EAC，AE=AB=CD，‎ ‎∵矩形ABCD的对边AB∥CD，‎ ‎∴∠DAC=∠BAC，‎ ‎∴∠EAC=∠DAC，‎ 设AE与CD相交于F，则AF=CF，‎ ‎∴AE﹣AF=CD﹣CF，‎ 即DF=EF，‎ ‎∴=，‎ 又∵∠AFC=∠EFD，‎ ‎∴△ACF∽△EDF，‎ ‎∴==，‎ 设DF=3x，FC=5x，则AF=5x，‎ 在Rt△ADF中，AD===4x，‎ 又∵AB=CD=DF+FC=3x+5x=8x，‎ ‎∴==．‎ 故选A．‎ 点评：‎ 本题考查了矩形的性质，平行线的性质，等角对等边的性质，相似三角形的判定与性质，勾股定理的应用，综合性较强，但难度不大，熟记各性质是解题的关键．‎ ‎8、（2013•湘西州）如图，在平面直角坐标系中，将点A（﹣2，3）向右平移3个单位长度后，那么平移后对应的点A′的坐标是（　　）‎ ‎　‎ A．‎ ‎（﹣2，﹣3）‎ B．‎ ‎（﹣2，6）‎ C．‎ ‎（1，3）‎ D．‎ ‎（﹣2，1）‎ 考点：‎ 坐标与图形变化-平移．‎ 分析：‎ 根据平移时，点的坐标变化规律“左减右加”进行计算即可．‎ 解答：‎ 解：根据题意，从点A平移到点A′，点A′的纵坐标不变，横坐标是﹣2+3=1，‎ 故点A′的坐标是（1，3）．‎ 故选C．‎ 点评：‎ 此题考查了点的坐标变化和平移之间的联系，平移时点的坐标变化规律是“上加下减，左减右加”．‎ ‎9、（2013•郴州）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（　　）‎ ‎　‎ A．‎ ‎25°‎ B．‎ ‎30°‎ C．‎ ‎35°‎ D．‎ ‎40°‎ 考点：‎ 翻折变换（折叠问题）．3718684‎ 分析：‎ 先根据三角形内角和定理求出∠B的度数，再由图形翻折变换的性质得出∠CB′D的度数，再由三角形外角的性质即可得出结论．‎ 解答：‎ 解：∵在Rt△ACB中，∠ACB=90°，∠A=25°，‎ ‎∴∠B=90°﹣25°=65°，‎ ‎∵△CDB′由△CDB反折而成，‎ ‎∴∠CB′D=∠B=65°，‎ ‎∵∠CB′D是△AB′D的外角，‎ ‎∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°．‎ 故选D．‎ 点评：‎ 本题考查的是图形的翻折变换及三角形外角的性质，熟知图形反折不变性的性质是解答此题的关键．‎ ‎10、（2013•常德）如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为（　　）‎ ‎　‎ A．‎ B．‎ ‎3‎ C．‎ ‎1‎ D．‎ 考点：‎ 翻折变换（折叠问题）‎ 分析：‎ 首先利用勾股定理计算出AC的长，再根据折叠可得△DEC≌△D′EC，设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，再根据勾股定理可得方程22+x2=（4﹣x）2，再解方程即可．‎ 解答：‎ 解：∵AB=3，AD=4，‎ ‎∴DC=3，‎ ‎∴AC==5，‎ 根据折叠可得：△DEC≌△D′EC，‎ ‎∴D′C=DC=3，DE=D′E，‎ 设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，‎ 在Rt△AED′中：（AD′）2+（ED′）2=AE2，‎ ‎22+x2=（4﹣x）2，‎ 解得：x=，‎ 故选：A．‎ 点评：‎ 此题主要考查了图形的翻着变换，以及勾股定理的应用，关键是掌握折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．‎ ‎11、（2013•十堰）如图，将△ABC沿直线DE折叠后，使得点B与点A重合．已知AC=5cm，△ADC的周长为17cm，则BC的长为（　　）‎ ‎　‎ A．‎ ‎7cm B．‎ ‎10cm C．‎ ‎12cm D．‎ ‎22cm 考点：‎ 翻折变换（折叠问题）．3718684‎ 分析：‎ 首先根据折叠可得AD=BD，再由△ADC的周长为17cm可以得到AD+DC的长，利用等量代换可得BC的长．‎ 解答：‎ 解：根据折叠可得：AD=BD，‎ ‎∵△ADC的周长为17cm，AC=5cm，‎ ‎∴AD+DC=17﹣5=12（cm），‎ ‎∵AD=BD，‎ ‎∴BD+CD=12cm．‎ 故选：C．‎ 点评：‎ 此题主要考查了翻折变换，关键是掌握折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．‎ ‎12、（2013•荆门）在平面直角坐标系中，线段OP的两个端点坐标分别是O（0，0），P（4，3），将线段OP绕点O逆时针旋转90°到OP′位置，则点P′的坐标为（　　）‎ ‎　‎ A．‎ ‎（3，4）‎ B．‎ ‎（﹣4，3）‎ C．‎ ‎（﹣3，4）‎ D．‎ ‎（4，﹣3）‎ 考点：‎ 坐标与图形变化-旋转．3718684‎ 专题：‎ 数形结合．‎ 分析：‎ 如图，把线段OP绕点O逆时针旋转90°到OP′位置看作是把Rt△OPA绕点O逆时针旋转90°到RtOP′A′，再根据旋转的性质得到OA′、P′A′的长，然后根据第二象限点的坐标特征确定P′点的坐标．‎ 解答：‎ 解：如图，OA=3，PA=4，‎ ‎∵线段OP绕点O逆时针旋转90°到OP′位置，‎ ‎∴OA旋转到x轴负半轴OA′的位置，∠P′A′0=∠PAO=90°，P′A′=PA=4，‎ ‎∴P′点的坐标为（﹣3，4）．‎ 故选C．‎ 点评：‎ 本题考查了坐标与图形变化﹣旋转：在直角坐标系中线段的旋转问题转化为直角三角形的旋转，然后利用旋转的性质求出相应的线段长，再根据点的坐标特征确定点的坐标．‎ ‎13、（2013成都市）如图，将矩形ABCD沿对角线BD折叠，使点C与点C’重合。若AB=2，则的长为（ ）‎ A.1 B‎.2 ‎ C.3 D.4‎ 答案：B 解析：由折叠可知，＝CD＝AB＝2。‎ ‎14、（2013•绥化）如图，在Rt△ABC中，∠C=90°，AC=，BC=1，D在AC上，将△ADB沿直线BD翻折后，点A落在点E处，如果AD⊥ED，那么△ABE的面积是（　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ C．‎ D．‎ 考点：‎ 翻折变换（折叠问题）．‎ 分析：‎ 先根据勾股定理计算出AB=2，根据含30度的直角三角形三边的关系得到∠BAC=30°，在根据折叠的性质得BE=BA=2，∠BED=∠BAD=30°，DA=DE，由于AD⊥ED得BC∥DE，所以∠CBF=∠BED=30°，在Rt△BCF中可计算出CF=，BF=2CF=，则EF=2﹣，在Rt△DEF中计算出FD=1﹣，ED=﹣1，然后利用S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE计算即可．‎ 解答：‎ 解：∵∠C=90°，AC=，BC=1，‎ ‎∴AB==2，‎ ‎∴∠BAC=30°，‎ ‎∵△ADB沿直线BD翻折后，点A落在点E处，‎ ‎∴BE=BA=2，∠BED=∠BAD=30°，DA=DE，‎ ‎∵AD⊥ED，‎ ‎∴BC∥DE，‎ ‎∴∠CBF=∠BED=30°，‎ 在Rt△BCF中，CF==，BF=2CF=，‎ ‎∴EF=2﹣，‎ 在Rt△DEF中，FD=EF=1﹣，ED=FD=﹣1，‎ ‎∴S△ABE=S△ABD+S△BED+S△ADE ‎=2S△ABD+S△ADE ‎=2×BC•AD+AD•ED ‎=2××1×（﹣1）+×（﹣1）（﹣1）‎ ‎=1．‎ 故选A．‎ 点评：‎ 本题考查了折叠问题：折叠前后两图形全等，即对应线段相等；对应角相等．也考查了勾股定理和含30度的直角三角形三边的关系．‎ ‎15、（2013•牡丹江）如图，△ABO中，AB⊥OB，OB=，AB=1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1的坐标为（　　）‎ ‎　‎ A．‎ ‎（﹣1，）‎ B．‎ ‎（﹣1，）或（﹣2，0）‎ C．‎ ‎（，﹣1）或（0，﹣2）‎ D．‎ ‎（，﹣1）‎ 考点：‎ 坐标与图形变化-旋转．3718684‎ 分析：‎ 需要分类讨论：在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标．‎ 解答：‎ 解：∵△ABO中，AB⊥OB，OB=，AB=1，‎ ‎∴tan∠AOB==，‎ ‎∴∠AOB=30°．‎ 如图1，当△ABO绕点O顺时针旋转150°后得到△A1B1O，则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°，‎ 则易求A1（﹣1，﹣）；‎ 如图2，当△ABO绕点O逆时针旋转150°后得到△A1B1O，则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°，‎ 则易求A1（0，﹣2）；‎ 综上所述，点A1的坐标为（，﹣1）或（﹣2，0）；‎ 故选B．‎ 点评：‎ 本题考查了坐标与图形变化﹣﹣旋转．解题时，注意分类讨论，以防错解．‎ ‎16、（2013年广州市）在6×6方格中，将图2—①中的图形N平移后位置如图2—②所示，则图形N的平移方法中，正确的是（ ）‎ ‎ ‎ ‎ A 向下移动1格 B 向上移动1格 C 向上移动2格 D 向下移动2格 分析：根据题意，结合图形，由平移的概念求解 解：观察图形可知：从图1到图2，可以将图形N向下移动2格．故选D．‎ 点评：本题考查平移的基本概念及平移规律，是比较简单的几何图形变换．关键是要观察比较平移前后图形的位置．‎ ‎17、（2013台湾、19）附图（①）为一张三角形ABC纸片，P点在BC上．今将A折至P时，出现折线BD，其中D点在AC上，如图（②）所示．若△ABC的面积为80，△DBC的面积为50，则BP与PC的长度比为何？（　　）‎ ‎　 A．3：2 B．5：3 C．8：5 D．13：8‎ 考点：翻折变换（折叠问题）；三角形的面积．‎ 分析：由题意分别计算出△DBP与△DCP的面积，从而BP：PC=S△DBP：S△DCP，问题可解．‎ 解答：解：由题意可得：S△ABD=S△ABC﹣S△DBC=80﹣50=30．‎ 由折叠性质可知，S△DBP=S△ABD=30，‎ ‎∴S△DCP=S△DBC﹣S△DBP=50﹣30=20．‎ ‎∴BP：PC=S△DBP：S△DCP=30：20=3：2．‎ 故选A．‎ 点评：本题考查了折叠的性质：折叠前后的两个三角形是全等三角形，它们的面积相等．　‎ ‎18、（2013•苏州）如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若=，则=　　用含k的代数式表示）．‎ 考点：‎ 矩形的性质；翻折变换（折叠问题）．‎ 分析：‎ 根据中点定义可得DE=CE，再根据翻折的性质可得DE=EF，AF=AD，∠AFE=∠D=90°，从而得到CE=EF，连接EG，利用“HL”证明Rt△ECG和Rt△EFG全等，根据全等三角形对应边相等可得CG=FG，设CG=a，表示出GB，然后求出BC，再根据矩形的对边相等可得AD=BC，从而求出AF，再求出AG，然后利用勾股定理列式求出AB，再求比值即可．‎ 解答：‎ 解：∵点E是边CD的中点，‎ ‎∴DE=CE，‎ ‎∵将△ADE沿AE折叠后得到△AFE，‎ ‎∴DE=EF，AF=AD，∠AFE=∠D=90°，‎ ‎∴CE=EF，‎ 连接EG，‎ 在Rt△ECG和Rt△EFG中，，‎ ‎∴Rt△ECG≌Rt△EFG（HL），‎ ‎∴CG=FG，‎ 设CG=a，∵=，‎ ‎∴GB=ka，‎ ‎∴BC=CG+BG=a+ka=a（k+1），‎ 在矩形ABCD中，AD=BC=a（k+1），‎ ‎∴AF=a（k+1），‎ AG=AF+FG=a（k+1）+a=a（k+2），‎ 在Rt△ABG中，AB===2a，‎ ‎∴==．‎ 故答案为：．‎ 点评：‎ 本题考查了矩形的性质，全等三角形的判定与性质，勾股定理的应用，以及翻折变换的性质，熟记性质并作辅助线构造出全等三角形是解题的关键．‎ ‎19、（2013•衡阳）如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB=　70　°．‎ 考点：‎ 旋转的性质．‎ 专题：‎ 探究型．‎ 分析：‎ 直接根据图形旋转的性质进行解答即可．‎ 解答：‎ 解：∵将△OAB绕点O逆时针旋转100°得到△OA1B1，∠AOB=30°，‎ ‎∴△OAB≌△OA1B1，‎ ‎∴∠A1OB=∠AOB=30°．‎ ‎∴∠A1OB=∠A1OA﹣∠AOB=70°．‎ 故答案为：70．‎ 点评：‎ 本题考查的是旋转的性质，熟知图形旋转前后对应边、对应角均相等的性质是解答此题的关键．‎ ‎20、（2013•广安）将点A（﹣1，2）沿x轴向右平移3个单位长度，再沿y轴向下平移4个长度单位后得到点A′的坐标为　（2，﹣2）　．‎ 考点：‎ 坐标与图形变化-平移．3718684‎ 分析：‎ 根据点的平移规律，左右移，横坐标减加，纵坐标不变；上下移，纵坐标加减，横坐标不变即可解的答案．‎ 解答：‎ 解：∵点A（﹣1，2）沿x轴向右平移3个单位长度，再沿y轴向下平移4个长度单位后得到点A′，‎ ‎∴A′的坐标是（﹣1+3，2﹣4），‎ 即：（2，﹣2）．‎ 故答案为：（2，﹣2）．‎ 点评：‎ 此题主要考查了点的平移规律，正确掌握规律是解题的关键．‎ ‎21、（2013四川宜宾）如图，将面积为5的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，那么图中的四边形ACED的面积为　15　．‎ 考点：平移的性质．‎ 分析：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．‎ 解答：解：设点A到BC的距离为h，则S△ABC=BC•h=5，‎ ‎∵平移的距离是BC的长的2倍，‎ ‎∴AD=2BC，CE=BC，X Kb1. Co m ‎∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×5=15．‎ 故答案为：15．‎ 点评：本题考查了平移的性质，三角形的面积，主要用了对应点间的距离等于平移的距离的性质．　‎ ‎22、（2013•黄冈）如图，矩形ABCD中，AB=4，BC=3，边CD在直线l上，将矩形ABCD沿直线l作无滑动翻滚，当点A第一次翻滚到点A1位置时，则点A经过的路线长为　6π　．‎ 考点：‎ 弧长的计算；矩形的性质；旋转的性质．3481324‎ 专题：‎ 规律型．‎ 分析：‎ 如图根据旋转的性质知，点A经过的路线长是三段：①以90°为圆心角，AD长为半径的扇形的弧长；②以90°为圆心角，AB长为半径的扇形的弧长；③90°为圆心角，矩形ABCD对角线长为半径的扇形的弧长．‎ 解答：‎ 解：∵四边形ABCD是矩形，AB=4，BC=3，‎ ‎∴BC=AD=3，∠ADC=90°，对角线AC（BD）=5．‎ ‎∵根据旋转的性质知，∠ADA′=90°，AD=A′D=BC=3，‎ ‎∴点A第一次翻滚到点A′位置时，则点A′经过的路线长为：=．‎ 同理，点A′第一次翻滚到点A″位置时，则点A′经过的路线长为：=2π．‎ 点″第一次翻滚到点A1位置时，则点A″经过的路线长为：=．‎ 则当点A第一次翻滚到点A1位置时，则点A经过的路线长为：+2π+=6π．‎ 故答案是：6π．‎ 点评：‎ 本题考查了弧长的计算、矩形的性质以及旋转的性质．根据题意画出点A运动轨迹，是突破解题难点的关键．‎ ‎23、（2013•包头）如图，在三角形纸片ABC中，∠C=90°，AC=6，折叠该纸片，使点C落在AB边上的D点处，折痕BE与AC交于点E，若AD=BD，则折痕BE的长为　4　．‎ 考点：‎ 翻折变换（折叠问题）．3718684‎ 专题：‎ 探究型．‎ 分析：‎ 先根据图形翻折变换的性质得出BC=BD，∠BDE=∠C=90°，再根据AD=BD可知AB=2BC，AE=BE，故∠A=30°，由锐角三角函数的定义可求出BC的长，设BE=x，则CE=6﹣x，在Rt△BCE中根据勾股定理即可得出BE的长．‎ 解答：‎ 解：∵△BDE△BCE反折而成，‎ ‎∴BC=BD，∠BDE=∠C=90°，‎ ‎∵AD=BD，‎ ‎∴AB=2BC，AE=BE，‎ ‎∴∠A=30°，‎ 在Rt△ABC中，‎ ‎∵AC=6，‎ ‎∴BC=AC•tan30°=6×=2，‎ 设BE=x，则CE=6﹣x，‎ 在Rt△BCE中，‎ ‎∵BC=2，BE=x，CE=6﹣x，‎ ‎∴BE2=CE2+BC2，即x2=（6﹣x）2+（2）2，解得x=4．‎ 故答案为：4．‎ 点评：‎ 本题考查的是图形的翻折变换，熟知图形反折不变性的性质是解答此题的关键．‎ ‎24、（2013•烟台）如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为　108　度．‎ 考点：‎ 线段垂直平分线的性质；等腰三角形的性质；翻折变换（折叠问题）．‎ 分析：‎ 连接OB、OC，根据角平分线的定义求出∠BAO，根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB，根据等边对等角可得∠ABO=∠BAO，再求出∠OBC，然后判断出点O是△ABC的外心，根据三角形外心的性质可得OB=OC，再根据等边对等角求出∠OCB=∠OBC，根据翻折的性质可得OE=CE，然后根据等边对等角求出∠COE，再利用三角形的内角和定理列式计算即可得解．‎ 解答：‎ 解：如图，连接OB、OC，‎ ‎∵∠BAC=54°，AO为∠BAC的平分线，‎ ‎∴∠BAO=∠BAC=×54°=27°，‎ 又∵AB=AC，‎ ‎∴∠ABC=（180°﹣∠BAC）=（180°﹣54°）=63°，‎ ‎∵DO是AB的垂直平分线，‎ ‎∴OA=OB，‎ ‎∴∠ABO=∠BAO=27°，‎ ‎∴∠OBC=∠ABC﹣∠ABO=63°﹣27°=36°，‎ ‎∵DO是AB的垂直平分线，AO为∠BAC的平分线，‎ ‎∴点O是△ABC的外心，‎ ‎∴OB=OC，‎ ‎∴∠OCB=∠OBC=36°，‎ ‎∵将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，‎ ‎∴OE=CE，‎ ‎∴∠COE=∠OCB=36°，‎ 在△OCE中，∠OEC=180°﹣∠COE﹣∠OCB=180°﹣36°﹣36°=108°．‎ 故答案为：108．‎ 点评：‎ 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，以及翻折变换的性质，综合性较强，难度较大，作辅助线，构造出等腰三角形是解题的关键．‎ ‎25、（2013•鄂州）如图，△AOB中，∠AOB=90°，AO=3，BO=6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为　　．‎ 考点：‎ 旋转的性质．3718684‎ 分析：‎ 利用勾股定理列式求出AB，根据旋转的性质可得AO=A′O，A′B′=AB，再求出OE，从而得到OE=A′O，过点O作OF⊥A′B′于F，利用三角形的面积求出OF，利用勾股定理列式求出EF，再根据等腰三角形三线合一的性质可得A′E=2EF，然后根据B′E=A′B′﹣A′E代入数据计算即可得解．‎ 解答：‎ 解：∵∠AOB=90°，AO=3，BO=6，‎ ‎∴AB===3，‎ ‎∵△AOB绕顶点O逆时针旋转到△A′OB′处，‎ ‎∴AO=A′O=3，A′B′=AB=3，‎ ‎∵点E为BO的中点，‎ ‎∴OE=BO=×6=3，‎ ‎∴OE=A′O，‎ 过点O作OF⊥A′B′于F，‎ S△A′OB′=×3•OF=×3×6，‎ 解得OF=，‎ 在Rt△EOF中，EF===，‎ ‎∵OE=A′O，OF⊥A′B′，‎ ‎∴A′E=2EF=2×=（等腰三角形三线合一），‎ ‎∴B′E=A′B′﹣A′E=3﹣=．‎ 故答案为：．‎ 点评：‎ 本题考查了旋转的性质，勾股定理的应用，等腰三角形三线合一的性质，以及三角形面积，熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．‎ ‎26、（2013年河北）如图11，四边形ABCD中，点M，N分别在AB，BC上， ‎ ‎ 将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，‎ ‎ 则∠B = °．‎ 答案：95‎ 解析：∠BNF＝∠C＝70°，∠BMF＝∠A＝100°，‎ ‎∠BMF＋∠B＋∠BNF＋∠F＝360°，所以，∠F＝∠B＝95°。‎ ‎27、(2013河南省)如图，矩形中，,点是边上一点，连接，把沿折叠，使点落在点处，当△为直角三角形时，的长为 ‎ ‎【解析】‎ ‎①当时，由题可知：,即：在同一直线上，落在对角线上，此时，设，则，，在中，解得 ‎②当时，即落在上，，此时在中，‎ 斜边大于直角边，因此这种情况不成立。‎ ‎③当时，即落在上，此时四边形是正方形，所以 ‎【答案】‎ ‎28、（2013安顺）如图，在平面直角坐标系中，将线段AB绕点A按逆时针方向旋转90°后，得到线段AB′，则点B′的坐标为 ．‎ 考点：坐标与图形变化-旋转．‎ 分析：画出旋转后的图形位置，根据图形求解．‎ 解答：解：AB旋转后位置如图所示．‎ B′（4，2）．‎ 点评：本题涉及图形旋转，体现了新课标的精神，抓住旋转的三要素：旋转中心A，旋转方向逆时针，旋转角度90°，通过画图得B′坐标．　‎ ‎29、(2013年广东省4分、15)如题15图，将一张直角三角板纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,‎ 则四边形ACE′E的形状是________________.‎ 答案：平行四边形 解析：C平行且等于BE，而BE＝EA，且在同一直线上，所以，C平行且等于AE，故是平行四边形。‎ ‎30、（2013年广州市）如图6，的斜边AB=16, ‎ 绕点O顺时针旋转后得到，则的斜边上的中线的长度为_____________ . ‎ 分析：根据旋转的性质得到A′B′=AB=16，然后根据直角三角形斜边上的中线性质求解即可 解：∵Rt△ABC绕点O顺时针旋转后得到Rt△A′B′C′，‎ ‎∴A′B′=AB=16，‎ ‎∵C′D为Rt△A′B′C′的斜边A′B′上的中线，‎ ‎∴C′D=A′B′=8．‎ 故答案为8．‎ 点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了直角三角形斜边上的中线性质．‎ ‎31、（2013•温州）如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上，按要求画一个三角形，使它的顶点在方格的顶点上．‎ ‎（1）将△ABC平移，使点P落在平移后的三角形内部，在图甲中画出示意图；‎ ‎（2）以点C为旋转中心，将△ABC旋转，使点P落在旋转后的三角形内部，在图乙中画出示意图．‎ 考点：‎ 作图-旋转变换；作图-平移变换．3718684‎ 专题：‎ 图表型．‎ 分析：‎ ‎（1）根据网格结构，把△ABC向右平移后可使点P为三角形的内部的三个格点中的任意一个；‎ ‎（2）把△ABC绕点C顺时针旋转90°即可使点P在三角形内部．‎ 解答：‎ 解：（1）平移后的三角形如图所示；‎ ‎（2）如图所示，旋转后的三角形如图所示．‎ 点评：‎ 本题考查了利用旋转变换作图，利用平移变换作图，熟练掌握网格结构是解题的关键．‎ ‎32、（13年安徽省4分、14）已知矩形纸片ABCD中，AB=1，BC=2，将该纸片叠成一个平面图形，折痕EF不经过A点（E、F是该矩形边界上的点），折叠后点A落在A，处，给出以下判断：‎ ‎（1）当四边形A，CDF为正方形时，EF=‎ ‎（2）当EF=时，四边形A，CDF为正方形 ‎（3）当EF=时，四边形BA，CD为等腰梯形；‎ ‎（4）当四边形BA，CD为等腰梯形时，EF=。‎ ‎ 其中正确的是 （把所有正确结论序号都填在横线上）。‎ ‎33、（2013•巴中）△ABC在平面直角坐标系xOy中的位置如图所示．‎ ‎（1）作△ABC关于点C成中心对称的△A1B‎1C1．‎ ‎（2）将△A1B‎1C1向右平移4个单位，作出平移后的△A2B‎2C2．‎ ‎（3）在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）‎ 考点：‎ 作图-旋转变换；轴对称-最短路线问题；作图-平移变换．‎ 分析：‎ ‎（1）延长AC到A1，使得AC=A‎1C1，延长BC到B1，使得BC=B‎1C1，即可得出图象；‎ ‎（2）根据△A1B‎1C1将各顶点向右平移4个单位，得出△A2B‎2C2；‎ ‎（3）作出A1的对称点A′，连接A′C2，交x轴于点P，再利用相似三角形的性质求出P点坐标即可．‎ 解答：‎ 解；（1）如图所示：‎ ‎（2）如图所示：‎ ‎（3）如图所示：作出A1的对称点A′，连接A′C2，交x轴于点P，‎ 可得P点坐标为：（，0）．‎ 点评：‎ 此题主要考查了图形的平移与旋转和相似三角形的性质等知识，利用轴对称求求最小值问题是考试重点，同学们应重点掌握．‎ ‎34、（2013•张家界）如图，在方格纸上，以格点连线为边的三角形叫做格点三角形，请按要求完成下列操作：先将格点△ABC绕A点逆时针旋转90°得到△A1B‎1C1，再将△A1B‎1C1沿直线B‎1C1作轴反射得到△A2B‎2C2．‎ 考点：‎ 作图-旋转变换；作图-轴对称变换．3718684‎ 分析：‎ ‎△ABC绕A点逆时针旋转90°得到△A1B‎1C1，△A1B‎1C1沿直线B‎1C1作轴反射得出△A2B‎2C2即可．‎ 解答：‎ 解：如图所示：‎ 点评：‎ 此题主要考查了图形的旋转变换以及轴对称图形，根据已知得出对应点位置是解题关键．‎ ‎　‎ ‎35、（2013•淮安）如图，在边长为1个单位长度的小正方形组成的两格中，点A、B、C都是格点．‎ ‎（1）将△ABC向左平移6个单位长度得到得到△A1B1C1；‎ ‎（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．‎ 考点：‎ 作图-旋转变换；作图-平移变换．3718684‎ 分析：‎ ‎（1）将点A、B、C分别向左平移6个单位长度，得出对应点，即可得出△A1B1C1；‎ ‎（2）将点A、B、C分别绕点O按逆时针方向旋转180°，得出对应点，即可得出△A2B2C2．‎ 解答：‎ 解：（1）如图所示：△A1B1C1，即为所求；‎ ‎（2）如图所示：△A2B2C2，即为所求．‎ 点评：‎ 此题主要考查了图形的平移和旋转，根据已知得出对应点坐标是解题关键．‎ ‎36、（2013•眉山）如图，在11×11的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．‎ ‎（1）在图中作出△ABC关于直线l对称的△A1B‎1C1；（要求A与A1，B与B1，C与C1相对应）新 课 标 第 一 网 ‎（2）作出△ABC绕点C顺时针方向旋转90°后得到的△A2B‎2C；‎ ‎（3）在（2）的条件下直接写出点B旋转到B2所经过的路径的长．（结果保留π）‎ 考点：‎ 作图-旋转变换；弧长的计算；作图-轴对称变换．‎ 专题：‎ 作图题．‎ 分析：‎ ‎（1）根据网格结构找出点A、B、C关于直线l的对称点A1、B1、C1的位置，然后顺次连接即可；‎ ‎（2）根据网格结构找出点A、B绕点C顺时针旋转90°后的A2、B2的位置，然后顺次连接即可；‎ ‎（3）利用勾股定理列式求出BC的长，再根据弧长公式列式计算即可得解．‎ 解答：‎ 解：（1）△A1B‎1C1如图所示；‎ ‎（2）△A2B‎2C如图所示；‎ ‎（3）根据勾股定理，BC==，‎ 所以，点B旋转到B2所经过的路径的长==π．‎ 点评：‎ 本题考查了利用轴对称变换作图，利用旋转变换作图，以及弧长的计算，熟练掌握网格结构准确找出对应点的位置是解题的关键．‎ ‎37、（2013•昆明）在平面直角坐标系中，四边形ABCD的位置如图所示，解答下列问题：‎ ‎（1）将四边形ABCD先向左平移4个单位，再向下平移6个单位，得到四边形A1B‎1C1D1，画出平移后的四边形A1B‎1C1D1；新|课 | 标|第 |一| 网 ‎（2）将四边形A1B1C1D1绕点A1逆时针旋转90°，得到四边形A1B2C2D2，画出旋转后的四边形A1B2C2D2，并写出点C2的坐标．‎ 考点：‎ 作图-旋转变换；作图-平移变换．‎ 专题：‎ 作图题．‎ 分析：‎ ‎（1）根据网格结构找出点A、B、C、D平移后的对应点A1、B1、C1、D1的位置，然后顺次连接即可；‎ ‎（2）根据网格结构找出B1、C1、D1绕点A1逆时针旋转90°的对应点B2、C2、D2的位置，然后顺次连接即可，再根据平面直角坐标系写出点C2的坐标．‎ 解答：‎ 解：（1）四边形A1B1C1D1如图所示；‎ ‎（2）四边形A1B2C2D2如图所示，‎ C2（1，﹣2）．‎ 点评：‎ 本题考查了利用旋转变换作图，利用平移变换作图，熟练掌握网格结构，准确找出对应点的位置是解题的关键．‎ ‎38、（13年安徽省8分、17）如图，已知A（—3，—3），B（—2，—1），C（—1，—2）是直角坐标平面上三点。‎ ‎（1）请画出ΔABC关于原点O对称的ΔA1B‎1C1，‎ ‎（2）请写出点B关天y轴对称的点B2的坐标，若将点B2向上平移h个单位，使其落在ΔA1B‎1C1内部，指出h的取值范围。‎ ‎39、（2013•钦州）如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：‎ ‎（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．‎ ‎（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．‎ 考点：‎ 作图-旋转变换；作图-轴对称变换．3718684‎ 分析：‎ ‎（1）分别找出A、B、C三点关于x轴的对称点，再顺次连接，然后根据图形写出A点坐标；‎ ‎（2）将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后，得到相应的对应点A2、B2、C2，连接各对应点即得△A2B2C2．‎ 解答：‎ 解：（1）如图所示：点A1的坐标（2，﹣4）；‎ ‎（2）如图所示，点A2的坐标（﹣2，4）．‎ 点评：‎ 本题考查图形的轴对称变换及旋转变换．解答此类题目的关键是掌握旋转的特点，然后根据题意找到各点的对应点，然后顺次连接即可．‎ ‎40、（2013•郴州）在图示的方格纸中 ‎（1）作出△ABC关于MN对称的图形△A1B1C1；‎ ‎（2）说明△A2B2C2是由△A1B1C1经过怎样的平移得到的？‎ 考点：‎ 作图-轴对称变换；作图-平移变换．3718684‎ 专题：‎ 作图题．‎ 分析：‎ ‎（1）根据网格结构找出点A、B、C关于MN的对称点A1、B1、C1的位置，然后顺次连接即可；‎ ‎（2）根据平移的性质结合图形解答．‎ 解答：‎ 解：（1）△A1B1C1如图所示；‎ ‎（2）向右平移6个单位，再向下平移2个单位（或向下平移2个单位，再向右平移6个单位）．‎ 点评：‎ 本题考查了利用轴对称变换作图，利用平移变换作图，熟练掌握网格结构准确找出对应点的位置以及变化情况是解题的关键．‎ ‎41、（2013•常州）在Rt△ABC中，∠C=90°，AC=1，BC=，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：‎ 以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：‎ ‎∠ABC=　30°　，∠A′BC=　90°　，OA+OB+OC=　　．‎ 考点：‎ 作图-旋转变换．‎ 专题：‎ 作图题．‎ 分析：‎ 解直角三角形求出∠ABC=30°，然后过点B作BC的垂线，在截取A′B=AB，再以点A′为圆心，以AO为半径画弧，以点B为圆心，以BO为半径画弧，两弧相交于点O′，连接A′O′、BO′，即可得到△A′O′B；根据旋转角与∠ABC的度数，相加即可得到∠A′BC；‎ 根据直角三角形30°角所对的直角边等于斜边的一半求出AB=‎2AC，即A′B的长，再根据旋转的性质求出△BOO′是等边三角形，根据等边三角形的三条边都相等可得BO=OO′，等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°，然后求出C、O、A′、O′四点共线，再利用勾股定理列式求出A′C，从而得到OA+OB+OC=A′C．‎ 解答：‎ 解：∵∠C=90°，AC=1，BC=，‎ ‎∴tan∠ABC===，‎ ‎∴∠ABC=30°，‎ ‎∵△AOB绕点B顺时针方向旋转60°，‎ ‎∴△A′O′B如图所示；‎ ‎∠A′BC=∠ABC+60°=30°+60°=90°，‎ ‎∵∠C=90°，AC=1，∠ABC=30°，‎ ‎∴AB=‎2AC=2，‎ ‎∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，‎ ‎∴A′B=AB=2，BO=BO′，A′O′=AO，‎ ‎∴△BOO′是等边三角形，‎ ‎∴BO=OO′，∠BOO′=∠BO′O=60°，‎ ‎∵∠AOC=∠COB=BOA=120°，‎ ‎∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°，‎ ‎∴C、O、A′、O′四点共线，‎ 在Rt△A′BC中，A′C===，‎ ‎∴OA+OB+OC=A′O′+OO′+OC=A′C=．‎ 故答案为：30°；90°；．‎ 点评：‎ 本题考查了利用旋转变换作图，旋转变换的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，勾股定理，等边三角形的判定与性质，综合性较强，最后一问求出C、O、A′、O′四点共线是解题的关键．‎ ‎42、（2013福省福州19）如图，在平面直角坐标系xOy中，点A的坐标为（﹣2，0），等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD．‎ ‎（1）△AOC沿x轴向右平移得到△OBD，则平移的距离是 个单位长度；△AOC与△BOD关于直线对称，则对称轴是 ；△AOC绕原点O顺时针旋转得到△DOB，则旋转角度可以是 度；‎ ‎（2）连结AD，交OC于点E，求∠AEO的度数．‎ 考点：旋转的性质；等边三角形的性质；轴对称的性质；平移的性质．‎ 专题：计算题．‎ 分析：（1）由点A的坐标为（﹣2，0），根据平移的性质得到△AOC沿x轴向右平移2个单位得到△OBD，则△AOC与△BOD关于y轴对称；根据等边三角形的性质得∠AOC=∠BOD=60°，则∠AOD=120°，根据旋转的定义得△AOC绕原点O顺时针旋转120°得到△DOB；‎ ‎（2）根据旋转的性质得到OA=OD，而∠AOC=∠BOD=60°，得到∠DOC=60°，所以OE为等腰△AOD的顶角的平分线，根据等腰三角形的性质得到OE垂直平分AD，则∠AEO=90°．‎ 解答：解：（1）∵点A的坐标为（﹣2，0），‎ ‎∴△AOC沿x轴向右平移2个单位得到△OBD；‎ ‎∴△AOC与△BOD关于y轴对称；‎ ‎∵△AOC为等边三角形，‎ ‎∴∠AOC=∠BOD=60°，‎ ‎∴∠AOD=120°，‎ ‎∴△AOC绕原点O顺时针旋转120°得到△DOB．‎ ‎（2）如图，∵等边△AOC绕原点O顺时针旋转120°得到△DOB，‎ ‎∴OA=OD，‎ ‎∵∠AOC=∠BOD=60°，‎ ‎∴∠DOC=60°，‎ 即OE为等腰△AOD的顶角的平分线，‎ ‎∴OE垂直平分AD，‎ ‎∴∠AEO=90°．‎ 故答案为2；y轴；120．‎ 点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等边三角形的性质、轴对称的性质以及平移的性质．　‎ ‎43、（2013•毕节地区）四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．‎ ‎（1）求证：△ADE≌△ABF；‎ ‎（2）填空：△ABF可以由△ADE绕旋转中心　A　 点，按顺时针方向旋转　90　 度得到；‎ ‎（3）若BC=8，DE=6，求△AEF的面积．‎ 考点：‎ 旋转的性质；全等三角形的判定与性质；正方形的性质．‎ 专题：‎ 证明题．‎ 分析：‎ ‎（1）根据正方形的性质得AD=AB，∠D=∠ABC=90°，然后利用“SAS”易证得△ADE≌△ABF；‎ ‎（2）由于△ADE≌△ABF得∠BAF=∠DAE，则∠BAF+∠EBF=90°，即∠FAE=90°，根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到；‎ ‎（3）先利用勾股定理可计算出AE=10，在根据△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到AE=AF，∠EAF=90°，然后根据直角三角形的面积公式计算即可．‎ 解答：‎ ‎（1）证明：∵四边形ABCD是正方形，‎ ‎∴AD=AB，∠D=∠ABC=90°，‎ 而F是DCB的延长线上的点，‎ ‎∴∠ABF=90°，‎ 在△ADE和△ABF中 ‎，‎ ‎∴△ADE≌△ABF（SAS）；‎ ‎（2）解：∵△ADE≌△ABF，‎ ‎∴∠BAF=∠DAE，‎ 而∠DAE+∠EBF=90°，‎ ‎∴∠BAF+∠EBF=90°，即∠FAE=90°，‎ ‎∴△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到；‎ 故答案为A、90；‎ ‎（3）解：∵BC=8，‎ ‎∴AD=8，‎ 在Rt△ADE中，DE=6，AD=8，‎ ‎∴AE==10，‎ ‎∵△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到，‎ ‎∴AE=AF，∠EAF=90°，‎ ‎∴△AEF的面积=AE2=×100=50（平方单位）．‎ 点评：‎ 本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了全等三角形的判定与性质以及勾股定理．‎ ‎44、（2013•遵义）如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N．‎ ‎（1）求证：CM=CN；‎ ‎（2）若△CMN的面积与△CDN的面积比为3：1，求的值．‎ 考点：‎ 矩形的性质；勾股定理；翻折变换（折叠问题）．3718684‎ 分析：‎ ‎（1）由折叠的性质可得：∠ANM=∠CNM，由四边形ABCD是矩形，可得∠ANM=∠CMN，则可证得∠CMN=∠CNM，继而可得CM=CN；‎ ‎（2）首先过点N作NH⊥BC于点H，由△CMN的面积与△CDN的面积比为3：1，易得MC=3ND=3HC，然后设DN=x，由勾股定理，可求得MN的长，继而求得答案．‎ 解答：‎ ‎（1）证明：由折叠的性质可得：∠ANM=∠CNM，‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD∥BC，‎ ‎∴∠ANM=∠CMN，‎ ‎∴∠CMN=∠CNM，‎ ‎∴CM=CN；‎ ‎（2）解：过点N作NH⊥BC于点H，‎ 则四边形NHCD是矩形，‎ ‎∴HC=DN，NH=DC，‎ ‎∵△CMN的面积与△CDN的面积比为3：1，‎ ‎∴===3，‎ ‎∴MC=3ND=3HC，‎ ‎∴MH=2HC，‎ 设DN=x，则HC=x，MH=2x，‎ ‎∴CM=3x=CN，‎ 在Rt△CDN中，DC==2x，‎ ‎∴HN=2x，‎ 在Rt△MNH中，MN==2x，‎ ‎∴==2．‎ 点评：‎ 此题考查了矩形的性质、折叠的性质、勾股定理以及三角形的面积．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用．‎ ‎45、（2013•徐州）如图，在Rt△ABC中，∠C=90°，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E、F分别在边AC、BC上）‎ ‎（1）若△CEF与△ABC相似．‎ ‎①当AC=BC=2时，AD的长为　　；‎ ‎②当AC=3，BC=4时，AD的长为　1.8或2.5　；‎ ‎（2）当点D是AB的中点时，△CEF与△ABC相似吗？请说明理由．‎ 考点：‎ 相似三角形的判定与性质；翻折变换（折叠问题）．‎ 分析：‎ ‎（1）若△CEF与△ABC相似．‎ ‎①当AC=BC=2时，△ABC为等腰直角三角形；‎ ‎②当AC=3，BC=4时，分两种情况：‎ ‎（I）若CE：CF=3：4，如答图2所示，此时EF∥AB，CD为AB边上的高；‎ ‎（II）若CF：CE=3：4，如答图3所示．由相似三角形角之间的关系，可以推出∠A=∠ECD与∠B=∠FCD，从而得到CD=AD=BD，即D点为AB的中点；‎ ‎（2）当点D是AB的中点时，△CEF与△ABC相似．可以推出∠CFE=∠A，∠C=∠C，从而可以证明两个三角形相似．‎ 解答：‎ 解：（1）若△CEF与△ABC相似．‎ ‎①当AC=BC=2时，△ABC为等腰直角三角形，如答图1所示．‎ 此时D为AB边中点，AD=AC=．‎ ‎②当AC=3，BC=4时，有两种情况：‎ ‎（I）若CE：CF=3：4，如答图2所示．‎ ‎∵CE：CF=AC：BC，∴EF∥BC．‎ 由折叠性质可知，CD⊥EF，∴CD⊥AB，即此时CD为AB边上的高．‎ 在Rt△ABC中，AC=3，BC=4，∴BC=5，∴cosA=．‎ AD=AC•cosA=3×=1.8；‎ ‎（II）若CF：CE=3：4，如答图3所示．‎ ‎∵△CEF∽△CAB，∴∠CEF=∠B．‎ 由折叠性质可知，∠CEF+∠ECD=90°，‎ 又∵∠A+∠B=90°，‎ ‎∴∠A=∠ECD，∴AD=CD．‎ 同理可得：∠B=∠FCD，CD=BD，‎ ‎∴此时AD=AB=×5=2.5．‎ 综上所述，当AC=3，BC=4时，AD的长为1.8或2.5．‎ ‎（2）当点D是AB的中点时，△CEF与△ABC相似．理由如下：‎ 如答图3所示，连接CD，与EF交于点Q．‎ ‎∵CD是Rt△ABC的中线，∴CD=DB=AB，∴∠DCB=∠B．‎ 由折叠性质可知，∠CQF=∠DQF=90°，∴∠DCB+∠CFE=90°，‎ ‎∵∠B+∠A=90°，∴∠CFE=∠A，‎ 又∵∠C=∠C，∴△CEF∽△CBA．‎ 点评：‎ 本题是几何综合题，考查了几何图形折叠问题和相似三角形的判定与性质．第（1）②问需要分两种情况分别计算，此处容易漏解，需要引起注意．‎ ‎46、(2013河南省)如图1，将两个完全相同的三角形纸片和重合放置，其中.‎ ‎（1）操作发现 如图2，固定，使绕点旋转。当点恰好落在边上时，填空：‎ ① 线段与的位置关系是 ；‎ ② 设的面积为，的面积为。则与的数量关系是 。‎ ‎【解析】①由旋转可知：AC=DC，‎ ‎∵，∴‎ ‎∴△ADC是等边三角形，∴,又∵‎ ‎∴∥‎ ‎ ②过D作DN⊥AC交AC于点N，过E作EM⊥AC交AC延长线于M，过C作CF⊥AB交AB于点F。‎ ‎ 由①可知：△ADC是等边三角形,∥，∴DN=CF,DN=EM ‎ ∴CF=EM ‎ ∵，∴,又∵‎ ‎ ∴‎ ‎ ∵ ∴=‎ ‎（2）猜想论证 ‎ 当绕点旋转到图3所示的位置时，小明猜想（1）中与的数量关系仍然成立，并尝试分别作出了和中边上的高，请你证明小明的猜想。‎ ‎【证明】∵‎ ‎ 又∵‎ ‎ 又∵‎ ‎ ∴△ANC≌△DMC ‎ ∴AN=DM ‎ 又∵CE=CB,∴‎ ‎（3）拓展探究 ‎ 已知，点是其角平分线上一点，，交于点（如图4），若在射线上存在点，使,请直接写出相应的的长 ‎【解析】如图所示，作∥交于点,作交于点。‎ 按照（1）（2）求解的方法可以计算出 ‎ ‎ 新课标第一网系列资料 www.xkb1.com ‎