2019中考数学压轴题精选十九

2019中考数学压轴题精选十九

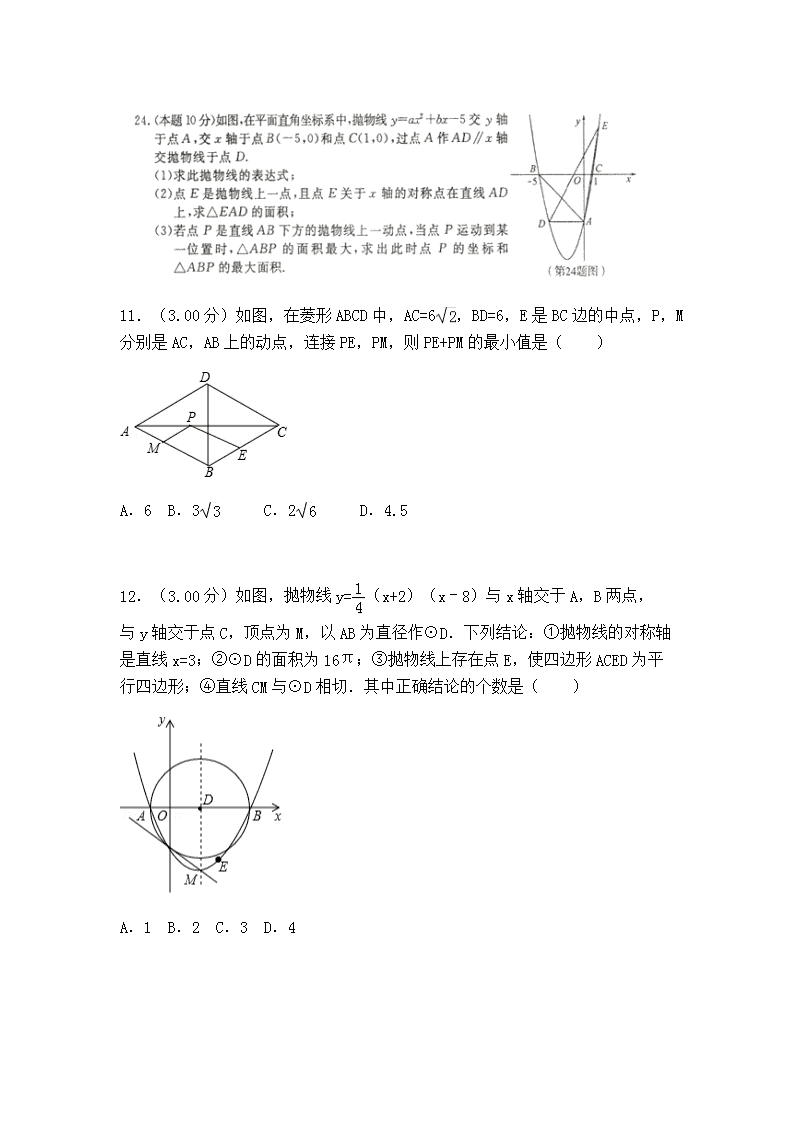
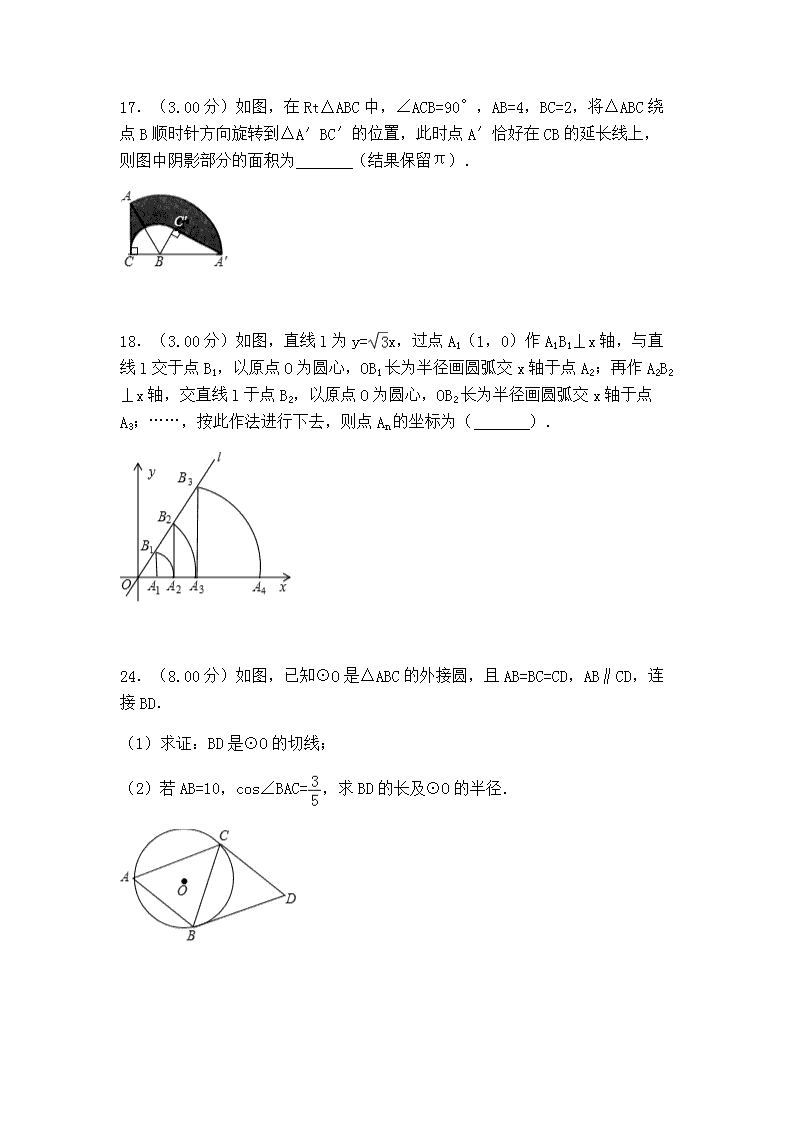
‎11．（3.00分）如图，在菱形ABCD中，AC=6，BD=6，E是BC边的中点，P，M分别是AC，AB上的动点，连接PE，PM，则PE+PM的最小值是（　　）‎ A．6 B．3 C．2 D．4.5‎ ‎12．（3.00分）如图，抛物线y=（x+2）（x﹣8）与x轴交于A，B两点，与y轴交于点C，顶点为M，以AB为直径作⊙D．下列结论：①抛物线的对称轴是直线x=3；②⊙D的面积为16π；③抛物线上存在点E，使四边形ACED为平行四边形；④直线CM与⊙D相切．其中正确结论的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎17．（3.00分）如图，在Rt△ABC中，∠ACB=90°，AB=4，BC=2，将△ABC绕点B顺时针方向旋转到△A′BC′的位置，此时点A′恰好在CB的延长线上，则图中阴影部分的面积为　 　（结果保留π）．‎ ‎18．（3.00分）如图，直线l为y=x，过点A1（1，0）作A1B1⊥x轴，与直线l交于点B1，以原点O为圆心，OB1长为半径画圆弧交x轴于点A2；再作A2B2⊥x轴，交直线l于点B2，以原点O为圆心，OB2长为半径画圆弧交x轴于点A3；……，按此作法进行下去，则点An的坐标为（　 　）．‎ ‎24．（8.00分）如图，已知⊙O是△ABC的外接圆，且AB=BC=CD，AB∥CD，连接BD．‎ ‎（1）求证：BD是⊙O的切线；‎ ‎（2）若AB=10，cos∠BAC=，求BD的长及⊙O的半径．‎ ‎25．（11.00分）如图，已知二次函数y=ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．‎ ‎（1）求这个二次函数的表达式；‎ ‎（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．‎ ‎①求线段PM的最大值；‎ ‎②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．‎ ‎26．（10.00分）已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持∠ABP=90°不变，BP边与直线l相交于点P．‎ ‎（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；‎ ‎（2）请利用如图1所示的情形，求证：=；‎ ‎（3）若AO=2，且当MO=2PO时，请直接写出AB和PB的长．‎ ‎25．（10.00分）如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，过点A作⊙O的切线交BC的延长线于点D．‎ ‎（1）求证：△DAC∽△DBA；‎ ‎（2）过点C作⊙O的切线CE交AD于点E，求证：CE=AD；‎ ‎（3）若点F为直径AB下方半圆的中点，连接CF交AB于点G，且AD=6，AB=3，求CG的长．‎ ‎26．（10.00分）如图，抛物线y=ax2+bx+c与x轴交于A（，0），B两点（点B在点A的左侧），与y轴交于点C，且OB=3OA=OC，∠OAC的平分线AD交y轴于点D，过点A且垂直于AD的直线l交y轴于点E，点P是x轴下方抛物线上的一个动点，过点P作PF⊥x轴，垂足为F，交直线AD于点H．‎ ‎（1）求抛物线的解析式；‎ ‎（2）设点P的横坐标为m，当FH=HP时，求m的值；‎ ‎（3）当直线PF为抛物线的对称轴时，以点H为圆心，HC为半径作⊙H，点Q为⊙H上的一个动点，求AQ+EQ的最小值．‎