- 2021-05-10 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2011中考数学一轮复习几何篇23圆中成比例的线段
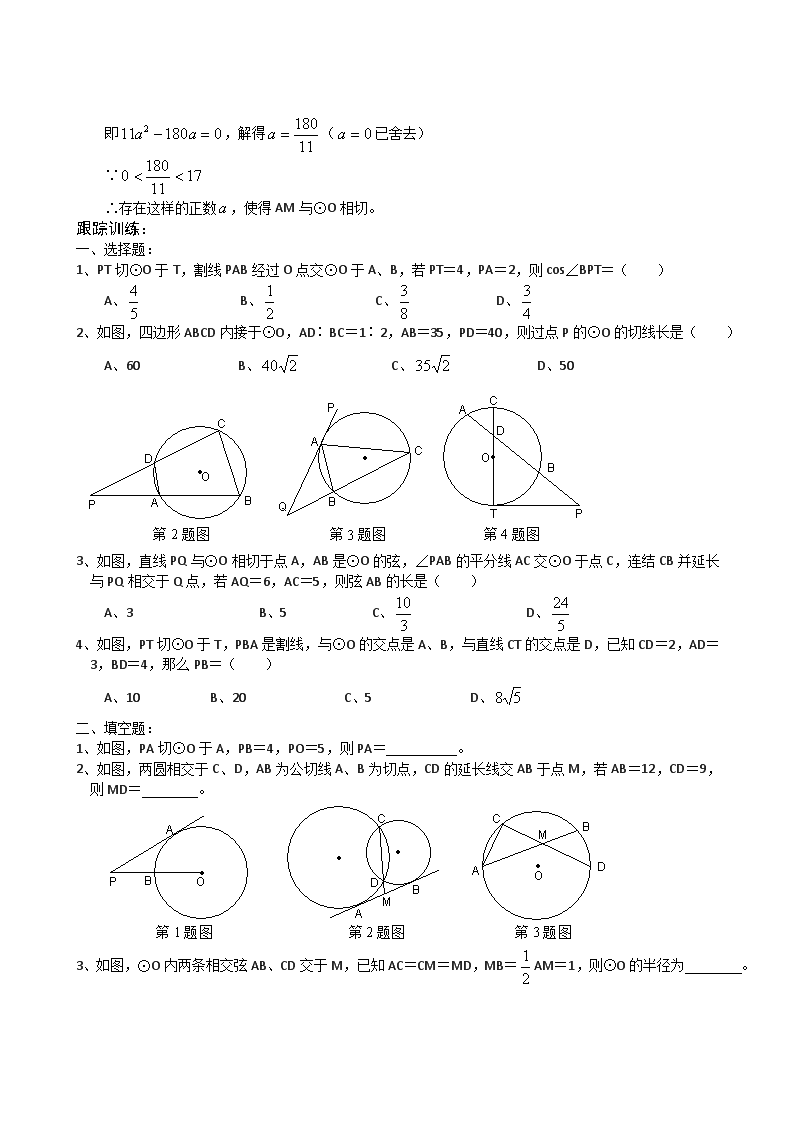
23.圆中成比例的线段 知识考点: 1、相交弦定理、切割线定理、割线定理是圆中成比例线段的重要的结论,是解决有关圆中比例线段问题的有力工具。 2、掌握和圆有关的比例线段的综合运用,主要是用于计算线段的长。 精典例题: 【例1】已知如图,AD为⊙O的直径,AB为⊙O的切线,割线BMN交AD的延长线于C,且BM=MN=NC,若AB=2。求: (1)BC的长; (2)⊙O的半径。 分析:由题设图形不难可以看出在本题中可综合运用勾股定理、切割线定理、割线定理来解题。 解:(1)设BM=MN=NC=,由切割线定理可得: 即解得:,∴BC=; (2)在Rt△ABC中,AC= 由割线定理可得: ∴ ∴ 【例2】如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E,求的值。 分析:由切割线定理有,可得直径BC的长,要求,由△ACE∽△ADB得,也就是求CA、BA的长。 解:连结CE ∵PA是⊙O的切线,PBC是⊙O的割线 ∴ 又PA=10,PB=5,∴PC=20,BC=15 ∵PA切⊙O于A,∴∠PAB=∠ACP 又∠P为公共角,△PAB∽△PCA ∴ ∵BC为⊙O的直径,∴∠CAB=900 ∴ ∴AC=,AB= 又∠ABC=∠E,∠CAE=∠EAB ∴△ACE∽△ADB,∴ ∴ 【例3】如图,AB切⊙O于A,D为⊙O内一点,且OD=2,连结BD交⊙O于C,BC=CD=3,AB=6,求⊙O的半径。 分析:把“图形”补成切割线定理、相交弦定理图形,问题就解决了。 解:延长BD交⊙O于E,两方延长OD交⊙O于F、G,设⊙O的半径为 ∵BA切⊙O于A,∴ ∵AB=6,BC=3,∴BE=12,ED=6 又,FD=-OD,DG=+OD ∴,OD=2 ∴, 探索与创新: 【问题一】如图,已知AB切⊙O于点B,AB的垂直平分线CF交AB于C,交⊙O于D、E,设点M是射线CF上的任一点,CM=,连结AM,若CB=3,DE=8。探索: (1)当M在线段DE(不含端点E)上时,延长AM交⊙O于点N,连结NE,若△ACM∽△NEM,请问:EN与AB的大小关系。 分析:如图1,由△ACM∽△NEM可得∠NEM=900,连结BO并延长交EN于G,可证BO垂直平分EN,即可证明EN=AB,结论就探索出来了。 解:∵AB的垂直平分线CF交AB于C,CB=3 ∴AB=6,∠ACM=900 又∵△ACM∽△NEM,∴∠NEM=900 连结BO并延长交EN于点G ∵CB切⊙O于B,∴∠GBC=900 ∴∠GBC=∠BCE=∠GEC=900 ∴四边BCEG是矩形 ∴∠EGB=900,G为NE的中点 ∴EN=2EG==2CB=6=AB (2)如图,当M在射线EF上时,若为小于17的正数,问是否存在这样的,使得AM与⊙O相切?若存在,求出的值;若不存在,试说明理由。 分析:先满足AM与⊙O相切,求出相应的值,看它是否是小于17的正数即可。 解:当AM与⊙O相切于点P时,有MP=AM-AP=AM-AB=AM-6 ∵MC=,AC=3,∠ACM=900 ∴AM=,又MD=MC-CD= ME=MC-CE=, ∴ 即,解得(已舍去) ∵ ∴存在这样的正数,使得AM与⊙O相切。 跟踪训练: 一、选择题: 1、PT切⊙O于T,割线PAB经过O点交⊙O于A、B,若PT=4,PA=2,则cos∠BPT=( ) A、 B、 C、 D、 2、如图,四边形ABCD内接于⊙O,AD∶BC=1∶2,AB=35,PD=40,则过点P的⊙O的切线长是( ) A、60 B、 C、 D、50 3、如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB并延长与PQ相交于Q点,若AQ=6,AC=5,则弦AB的长是( ) A、3 B、5 C、 D、 4、如图,PT切⊙O于T,PBA是割线,与⊙O的交点是A、B,与直线CT的交点是D,已知CD=2,AD=3,BD=4,那么PB=( ) A、10 B、20 C、5 D、 二、填空题: 1、如图,PA切⊙O于A,PB=4,PO=5,则PA= 。 2、如图,两圆相交于C、D,AB为公切线A、B为切点,CD的延长线交AB于点M,若AB=12,CD=9,则MD= 。 3、如图,⊙O内两条相交弦AB、CD交于M,已知AC=CM=MD,MB=AM=1,则⊙O的半径为 。 4、如图,在△ABC中,AB=AC,∠C=720,⊙O过A、B两点且与BC相切于点B,与AC交于点D,连结BD,若BC=,则AC= 。 5、已知⊙O和⊙O内一点P,过P的直线交⊙O于A、B两点,若,OP=5,则⊙O的半径长为 。 6、如图,在Rt△ABC中,∠C=900,AB=,BC=,AC=,半径为1.2的⊙O与AC、BC相切,且圆心O在斜边AB上,则= 。 三、计算或证明题: 1、如图,已知Rt△ABC是⊙O的内接三角形,∠BAC=900,AH⊥BC,垂足为D,过点B作弦BF交AD于点E,交⊙O于点F,且AE=BE。 (1)求证:; (2)若,AD=6,求BD的长。 2、如图,AB是⊙O的直径,AC切⊙O于A,CB交⊙O于D,DE切⊙O于D,BE⊥DE于E,BD=10,DE、BE是方程的两个根,求AC的长。 3、如图,P是⊙O直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E。 (1)求证:; (2)若DE⊥CF,∠P=150,⊙O的半径为2,求弦CF的长。 4、如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F。 (1)求证:BC是⊙P的切线; (2)若CD=2,CB=,求EF的长; (3)若设=PE∶CE,是否存在实数,使△PBD是等边三角形?若存在,求出的值;若不存在,请说明理由。 跟踪训练参考答案 一、选择题:AACB 二、填空题: 1、;2、3;3、;4、2;5、7;6、8或9 三、计算或证明题: 1、(1)略;(2);(3); 2、略解:由已知可得, 又∵ ∴ 解得:,故BE=8,DE=6 由△ADB∽△DEB可得:AD= 由△ADC∽△BED可得:AC= 3、提示:(1)连结OD,证△PCE∽△POD得;(2)证∠ODE=150得∠HDO=∠EDC=300,∵OD=2,则DH=,DE=,CE=。∴CF=CE+EF= 4、(1)连结PA、PB,证∠PBC=900;(2)EF=;(3)存在,使△PBD为等边三角形。查看更多