中考数学中考试题分类汇编反比例函数

中考数学中考试题分类汇编反比例函数

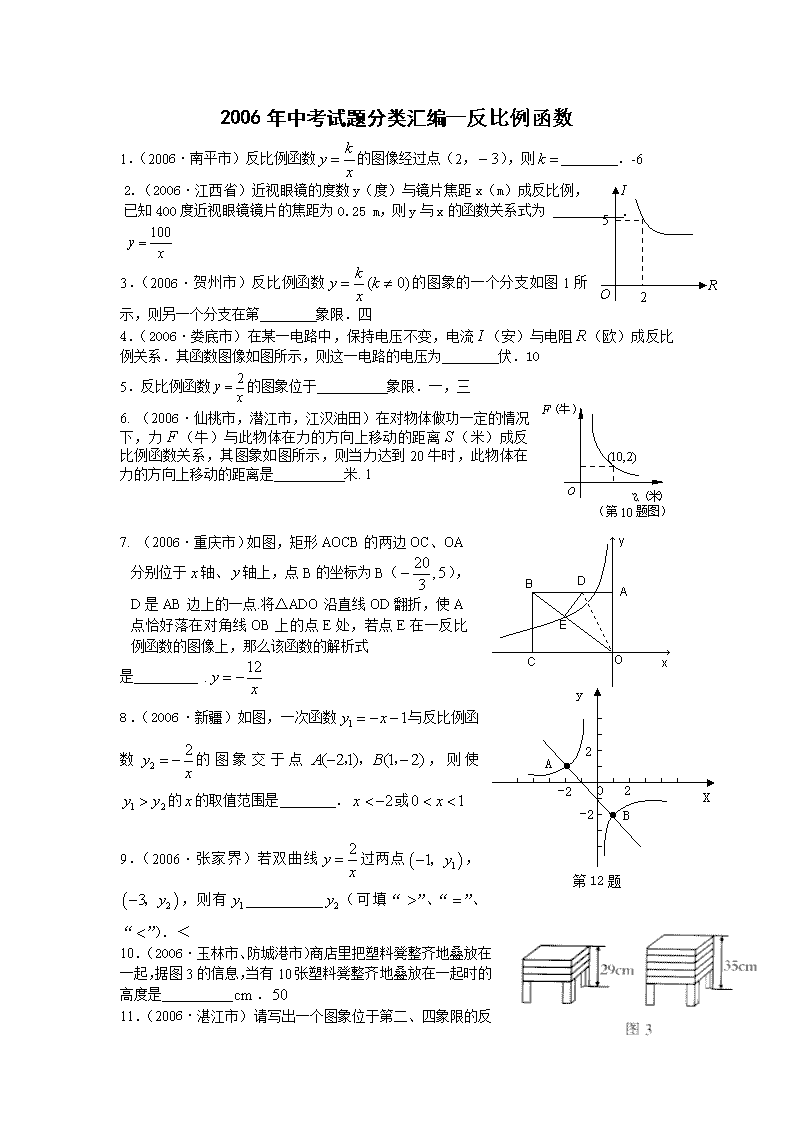
‎2006年中考试题分类汇编--反比例函数 R I O ‎5‎ ‎2‎ ‎1．（2006·南平市）反比例函数的图像经过点（2，），则 ．-6‎ ‎2. （2006·江 西 省）近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为‎0.25 m，则y与x的函数关系式为 . ‎ ‎3．（2006·贺州市）反比例函数的图象的一个分支如图1所示，则另一个分支在第　　　　象限．四 ‎4．（2006·娄底市）在某一电路中，保持电压不变，电流（安）与电阻（欧）成反比例关系．其函数图像如图所示，则这一电路的电压为 伏．10 ‎ ‎（米）‎ ‎（牛）‎ ‎ ‎ ‎（第10题图）‎ ‎5．反比例函数的图象位于　　　　　象限．一，三 ‎6. （2006·仙桃市，潜江市，江汉油田）在对物体做功一定的情况下，力（牛）与此物体在力的方向上移动的距离（米）成反比例函数关系，其图象如图所示，则当力达到20牛时，此物体在力的方向上移动的距离是 米. 1‎ ‎7. 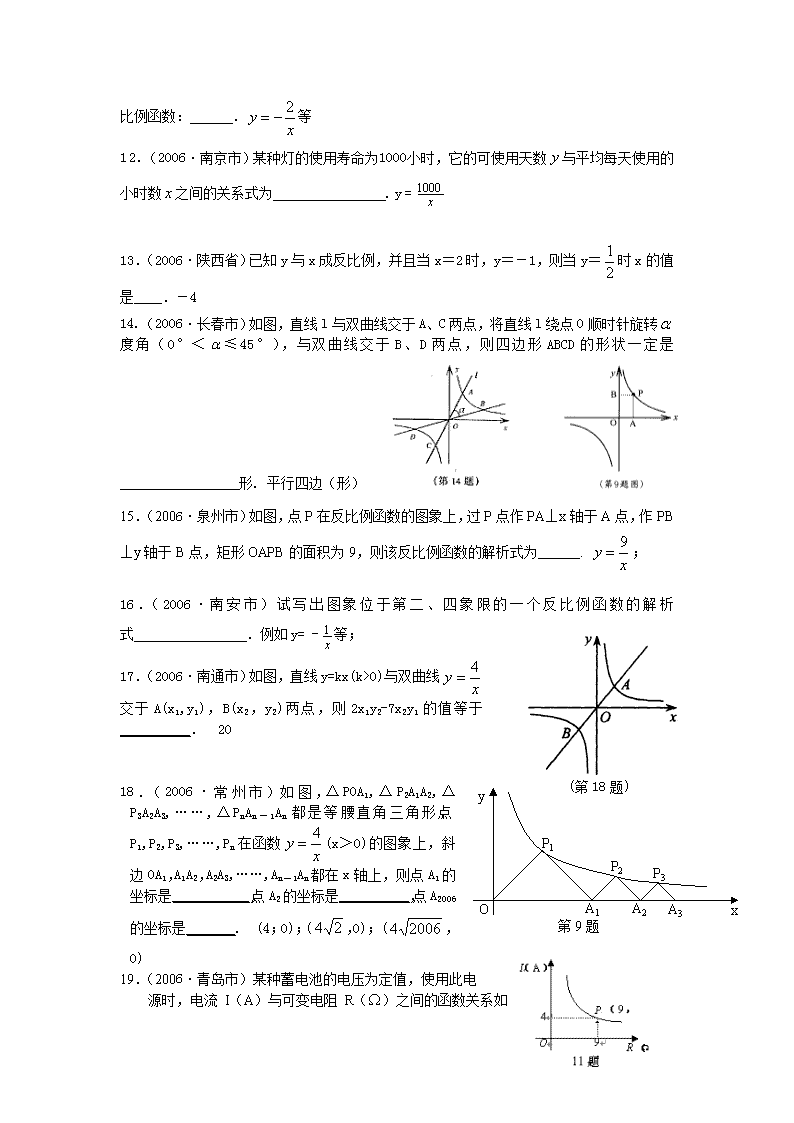（2006·重庆市）如图，矩形AOCB的两边OC、OA分别位于轴、轴上，点B的坐标为B（），D是AB边上的一点.将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图像上，那么该函数的解析式 O B A ‎-2‎ ‎-2‎ ‎2‎ ‎2‎ X y 第12题 是 .‎ ‎8．（2006·新疆）如图，一次函数与反比例函数的图象交于点，则使的的取值范围是　　　　．或 ‎9．（2006·张家界）若双曲线过两点，，则有___________（可填“”、“”、“”）．‎ ‎10．（2006·玉林市、防城港市）商店里把塑料凳整齐地叠放在一起，据图3的信息，当有10张塑料凳整齐地叠放在一起时的高度是 ．‎ ‎11．（2006·湛江市 ‎）请写出一个图象位于第二、四象限的反比例函数： ．等 ‎12. （2006·南京市）某种灯的使用寿命为1000小时，它的可使用天数与平均每天使用的小时数之间的关系式为 .y=‎ ‎13．（2006·陕西省）已知y与x成反比例，并且当x＝2时，y＝－1，则当y＝时x的值是____．－4‎ ‎14.（2006·长春市）如图，直线l与双曲线交于A、C两点，将直线l绕点O顺时针旋转度角（0°＜≤45°），与双曲线交于B、D两点，则四边形ABCD的形状一定是_________________形. 平行四边（形）‎ ‎15．（2006·泉州市）如图，点P在反比例函数的图象上，过P点作PA⊥x轴于A点，作PB⊥y轴于B点，矩形OAPB的面积为9，则该反比例函数的解析式为　　　. ； ‎ ‎(第18题)‎ ‎16．（2006·南安市）试写出图象位于第二、四象限的一个反比例函数的解析式 ．例如y= -等；‎ ‎17．（2006·南通市）如图，直线y=kx(k>0)与双曲线交于A(x1,y1)，B(x2，y2)两点，则2x1y2-7x2y1的值等于__________． 20‎ x O A1‎ A2‎ A3‎ P1‎ P2‎ P3‎ y 第9题 ‎18．（2006·常州市）如图，△POA1,△P‎2A1A2,△P‎3A2A3,……,△PnAn－1An都是等腰直角三角形，点P1,P2,P3,……,Pn在函数(x＞0)的图象上，斜边OA1，A‎1A2，A‎2A3,……,An－1An都在x轴上，则点A1的坐标是___________，点A2的坐标是__________，点A2006的坐标是_______. 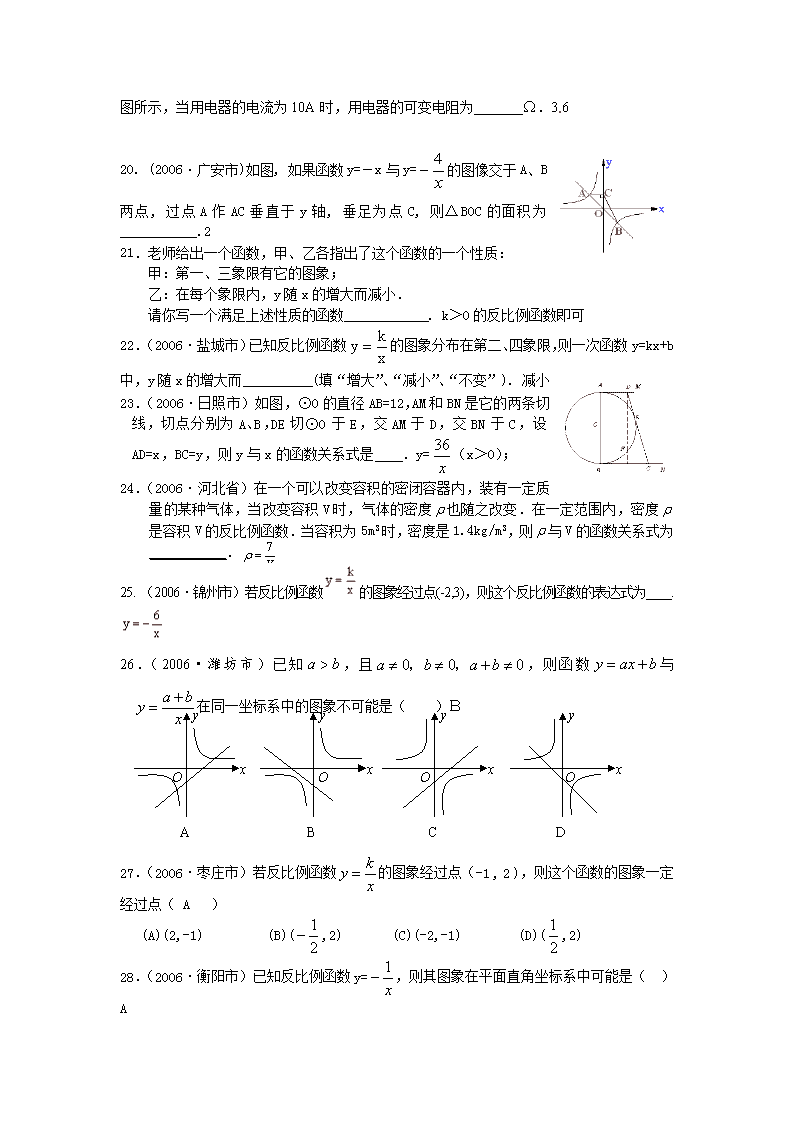(4；0)；(，0)；(，0)‎ ‎19．（2006·青岛市）某种蓄电池的电压为定值，使用此电 源时，电流 I（A）与可变电阻 R（Ω ‎）之间的函数关系如图所示，当用电器的电流为‎10A时，用电器的可变电阻为_______Ω．3.6‎ ‎20. (2006·广安市)如图, 如果函数y=－x与y=的图像交于A、B两点, 过点A作AC垂直于y轴, 垂足为点C, 则△BOC的面积为___________.2‎ ‎21．老师给出一个函数，甲、乙各指出了这个函数的一个性质：‎ ‎ 甲：第一、三象限有它的图象；‎ ‎ 乙：在每个象限内，y随x的增大而减小．‎ 请你写一个满足上述性质的函数____________. k＞0的反比例函数即可 ‎22．（2006·盐城市）已知反比例函数的图象分布在第二、四象限，则一次函数y=kx+b中，y随x的增大而 (填“增大”、“减小”、“不变”). 减小 ‎23．（2006·日照市）如图，⊙O的直径AB=12，AM和BN是它的两条切线，切点分别为A、B，DE切⊙O于E，交AM于D，交BN于C，设AD=x，BC=y，则y与x的函数关系式是 ．y=（x＞0）；‎ ‎24．（2006·河北省）在一个可以改变容积的密闭容器内，装有一定质量的某种气体，当改变容积V时，气体的密度也随之改变．在一定范围内，密度是容积V的反比例函数．当容积为‎5m3‎时，密度是‎1.4kg/m3，则与V的函数关系式为___________． ‎ ‎25. （2006·锦州市）若反比例函数的图象经过点(-2,3)，则这个反比例函数的表达式为____.　 ‎ O x y A．‎ O x y B．‎ O x y C．‎ O x y D．‎ ‎26．（2006·潍坊市）已知，且，则函数与在同一坐标系中的图象不可能是（ ）Ｂ ‎27．（2006·枣庄市）若反比例函数的图象经过点（-1 , 2 )，则这个函数的图象一定经过点（ A ）‎ ‎ (A)(2,-1) (B)(,2) (C)(-2,-1) (D)(,2)‎ ‎28．（2006·衡阳市）已知反比例函数y=，则其图象在平面直角坐标系中可能是（ ）A ‎ ‎29．（2006·绍兴市）如图，正方形OABC，ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数的图象上，则点E的坐标是( ) A A、　 　 B、　　 ‎ C、　　 　 D、 ‎ x O y x O y x O y x O y ‎30. （2006·攀枝花市）正比例函数与反比例函数在同一坐标系中的图象不可能是（　D　　　）‎ ‎ A B C D ‎31．（2006·淮安市）正比例函数与反比例函数图象都经过点(1，4)，在第一象限内正比例函数图象在反比例函数图象上方的自变量x的取值范围是（ A ） ‎ ‎ A．x>1 B．O4 D．00),那么（ ）‎ A、函数图象在一象限内,且y 随x的增大而减小;‎ B、函数图象在一象限内,且y 随x的增大而增大;‎ C、函数图象在二象限内,且y 随x的增大而减小;‎ D、函数图象在二象限内,且y 随x的增大而增大 ‎37．（2006·株洲市）若双曲线过点，则的值是 ．6‎ ‎38．（2006·湖州市）反比例函数的图像经过点（1，－3），则k的值为（ A ）‎ ‎ A、－3 B、‎3 ‎C、 D、－‎ ‎39．（2006·深圳市）函数的图象如图3所示，那么函数的图象大致是（ C ）‎ A B C D ‎ ‎ ‎40．（2006·梅州市）在同一平面直角坐标系中，直线与双曲线的交点个数为（　　）C Ａ．0个 Ｂ．1个 Ｃ．2个 Ｄ．无法确定 x y O A．‎ x y O B．‎ x y O C．‎ x y O D．‎ ‎41．（2006·娄底市）将函数与函数 的大致图象画在同一坐标系中，正确的函数图象是（ ）D ‎42．（2006·南宁市）下列反比例函数图象一定在一、三象限的是（　　）C Ａ． Ｂ． Ｃ． Ｄ．‎ ‎43. （2006·芜湖市）已知反比例函数y=的图象在第二、四象限，则m的取值范围是（ ）D A、m≥5 B、m>‎5 C、m≤5 D、m<5‎ ‎（第19题图）‎ ‎44．（2006·湘西自治州）在闭合电路中，电流，电压，‎ 电阻之间的关系为：．电压（伏特）一定时，电流（安培）关于电阻（欧姆）的函数关系的大致图象是（　　）A Ａ．‎ Ｂ．‎ Ｃ．‎ Ｄ．‎ ‎45．（2006·郴州市）某闭合电路中，电源电压不变，电流与电阻R()成反比例，图4表示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R M(4，2)‎ I(A)‎ R()‎ O 图4‎ 表示电流I的函数解析式为（　　）A Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ ‎46. （2006·邵阳市）函数y=的大致图像是（ ）D ‎ ‎ ‎ ‎47. （2006·浙江省） 如果两点（1，）和（2，）都在反比例函数的图象上，那么（ ）D A．＜＜0 B．＜＜‎0 C．＞＞0 D．＞＞0‎ ‎48. （2006·荆门市）已知函数y=-kx+4与y=的图象有两个不同的交点,且A(-,y1)、B(-1,y2)、C(,y3)在函数y=的图象上,则y1,y2,y3的大小关系是( )A ‎(A)y1＜y2＜y3. (B)y3＜y2＜y1. (C)y3＜y1＜y2. (D)y2＜y3＜y1.‎ ‎49.（2006·梅列区）如图,函数y=kx（x﹥0）与y=的图象交于A、B两点，过A、B点分别作x轴和y轴作垂线垂足为D、E，两线相交于C点。求S△ABC ‎50. （2006·资阳市）已知一次函数y=x+m与反比例函数的图象在第一象限的交点为P(x0，2).‎ ‎(1) 求x0及m的值；‎ ‎(2) 求一次函数的图象与两坐标轴的交点坐标. ‎ 解： (1) ∵ 点P(x0，2)在反比例函数y=的图象上，‎ ‎∴ 2=，解得x0=1. ‎ ‎∴ 点P的坐标为(1，2). ‎ 又∵ 点P在一次函数y=x+m的图象上，‎ ‎∴ 2=1+m，解得m=1. ‎ ‎∴ x0和m的值都为1 . ‎ ‎(无最后一步结论，不扣分)‎ ‎(2) 由(1)知，一次函数的解析式为y=x+1，取y=0，得x= -1；取x=0，得y=1 . ‎ ‎∴ 一次函数的图象与x轴的交点坐标为(-1,0)、与y轴的交点坐标为(0,1). ‎ ‎51．（2006·新疆）请你举出一个生活中能用反比例函数关系描述的实例，写出其函数表达式，并画出函数图象．‎ 举例：‎ ‎ ‎ 函数表达式：‎ 举例：要编织一块面积为‎2米2的矩形地毯，地毯的 长（米）与宽（米）之间的函数关系式为 ‎52．（2006·盐城市） 一司机驾驶汽车从甲地去乙地，以80千米/小时的平均速度用6小时到达目的地.(1)当他按原路匀速返回时，求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式；(2)如果该司机匀速返回时，用了48小时，求返回时的速度. ‎ 求得：s=‎480千米 (1)求得 (2)可求得：速度v=100(千米/小时)，‎ ‎53．（2006·十堰市）某校科技小组进行野外考察，途中遇到一片十几米宽的烂泥湿地．为了安全、迅速通过这片湿地，他们沿着前进路线铺了若干块木块，构筑成一条临时近道．木板对地面的压强是木板面积的反比例函数，其图象如下图所示．‎ ‎0‎ ‎200‎ ‎400‎ ‎600‎ ‎4‎ ‎3‎ ‎2.5‎ ‎2‎ ‎1.5 2‎ ‎1‎ ‎（1）请直接写出这一函数表达式和自变量取值范围；‎ ‎（2）当木板面积为时，压强是多少？‎ ‎（3）如果要求压强不超过，木板的面积至少要多大？‎ 解：（1）（解析式与自变量取值范围各1分）． ‎ ‎（2）当时，． ‎ 即压强是． ‎ ‎（3）由题意知，，．‎ 即木板面积至少要有． ‎ O A B x y ‎54．（2006·烟台市）如图，一次函数的图象与反比例函数图象交于 A（－2，1）、B（1，n）两点。‎ ‎（1）求反比例函数和一次函数的解析式； ‎ ‎（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。 ‎ ‎（1）；y＝－x－1 ‎ ‎ （2）x<-2或0”或“<”）。 <‎ ‎11、（河南省）双曲线y=和一次函数y=ax+b的图象的两交点分别是A（-1，-4），B（2，m），则a+2b=______________。 -2‎ ‎12、（绵阳市）若正比例函数y=mx（m≠0）和反比例函数y=（n≠0）的图象都经过点（2，3），则m=_________，n=_____________。 ，6‎ ‎13、（兰州市）已知函数y= -kx（k≠0）与y=的图象交于A、B两点，过点A作AC垂直于y轴，垂足为点C，则△BOC的面积为_________________。 2‎ ‎7、（长春市）图中正比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆，若点A的坐标为（1，2），则图中两个阴影面积的和是_______________。 π ‎14（徐州市）已知函数y=y1+y2，y1与x成正比例，y2与x成反比例，且当x=1时，y=-1；当x=3时，y=5，求y关于x的函数关系式。‎ 设y1=k1x，y2=，则y=k1x+‎ 由题意得： 解之得 ‎∴所求函数的关系式为y=2x－‎ ‎15、（安徽省）已知函数y1=x－1和y2=‎ ‎（1）在所给的坐标系中画出这两个函数的图象；‎ ‎（2）求这两个函数图象的交点坐标；‎ ‎（3）观察图象，当x在什么范围内时，y1>y2？‎ ‎16、（常德市）已知正比例函数y=kx与反比例函数y=的图象都过A（m，1）点，求此正比例函数解析式及另一个交点的坐标。 y=，（-3，-1）‎ ‎17．（北京市海淀区）已知反比例函数y=的图象经过点（4，），若一次函数y=x+1的图象平移后经过该反比反例函数图象上的点B（2，m），求平移后的一次函数图像与x轴的交点坐标。‎ 由于反比例函数y=的图象过点（4，），所以=，解得k=2，所以反比例函数的解析式为y=，又因为B（2，m）在y=的图象上，所以m==1，所以B（2，1）。设由y=x+1的图象平移后得到的函数解析式为y=x+b，由题意得y=x+b的图象过B（2，1），所以1=2+b，解得b= -1，故平移后的一次函数解析式为y=x－1，令y=0，则0=x－1，解得x=1，所以平移后的一次函数图象与x轴的交点坐标为（1，0）。‎ ‎18．（济南市）你吃过拉面吗？实际上在做接拉面的过程中就渗透数学知识，一定体积的面团做成拉面，面条的总长度y（m）是面条的粗细（横载面积）S（mm2）的反比例函数，其图象如图所示。‎ ‎（1）写出y与s的函数关第式；‎ ‎（2）求当面条粗‎1.6mm2时，面条的总长度是多少米？‎ ‎ ‎ ‎（1）y=；（2）‎‎80m ‎19、（四川省）如图，一次函数y=ax+b的图象与反比例函数y=的图象交于A、B两点，每x轴交于点C，与y轴交于点D，已知OA=，tan∠AOC=，点B的坐标为（，m）‎ ‎（1）求反比例函数和一次函数的解析式；‎ ‎（2）求△AOB的面积；‎