2012年各地中考数学压轴题精选1

2012年各地中考数学压轴题精选1

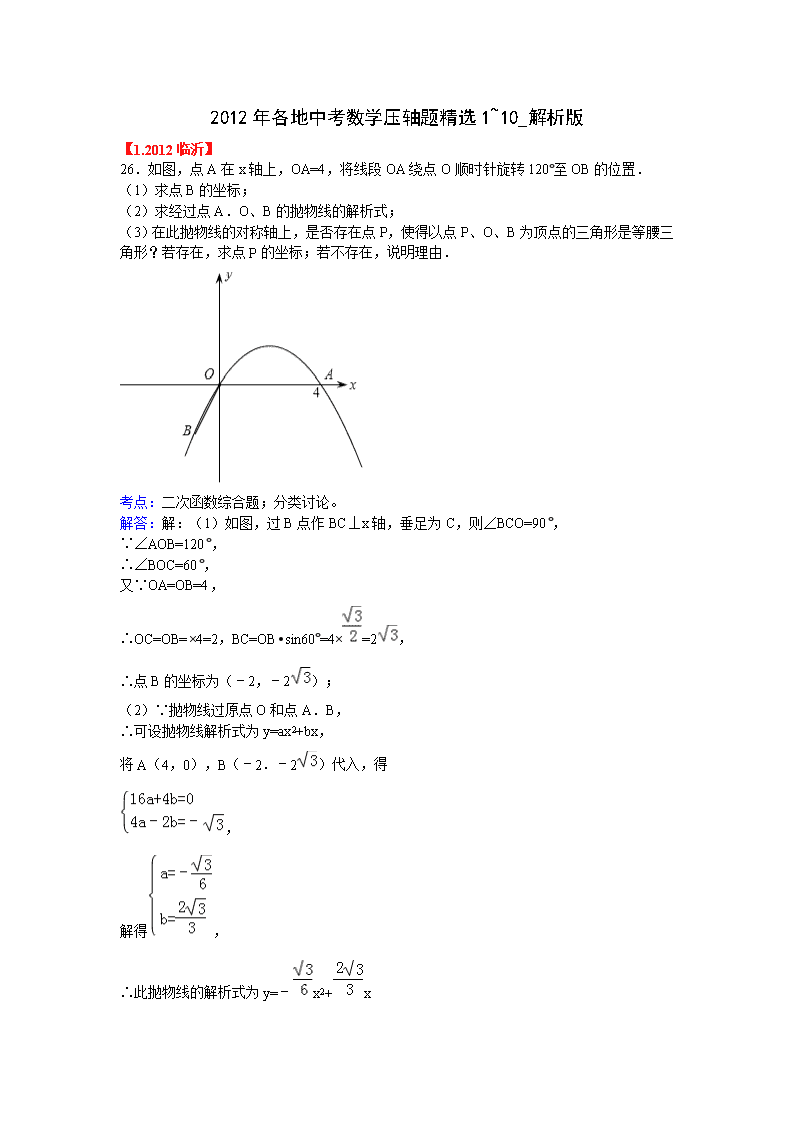
‎2012年各地中考数学压轴题精选1~10_解析版 ‎【1.2012临沂】‎ ‎26．如图，点A在x轴上，OA=4，将线段OA绕点O顺时针旋转120°至OB的位置．‎ ‎（1）求点B的坐标；‎ ‎（2）求经过点A．O、B的抛物线的解析式；‎ ‎（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，说明理由．‎ 考点：二次函数综合题；分类讨论。‎ 解答：解：（1）如图，过B点作BC⊥x轴，垂足为C，则∠BCO=90°，‎ ‎∵∠AOB=120°，‎ ‎∴∠BOC=60°，‎ 又∵OA=OB=4，‎ ‎∴OC=OB=×4=2，BC=OB•sin60°=4×=2，‎ ‎∴点B的坐标为（﹣2，﹣2）；‎ ‎（2）∵抛物线过原点O和点A．B，‎ ‎∴可设抛物线解析式为y=ax2+bx，‎ 将A（4，0），B（﹣2．﹣2）代入，得 ‎，‎ 解得，‎ ‎∴此抛物线的解析式为y=﹣x2+x ‎（3）存在，‎ 如图，抛物线的对称轴是x=2，直线x=2与x轴的交点为D，设点P的坐标为（2，y），‎ ‎①若OB=OP， ‎ 则22+|y|2=42，‎ 解得y=±2，‎ 当y=2时，在Rt△POD中，∠PDO=90°，sin∠POD==，‎ ‎∴∠POD=60°，‎ ‎∴∠POB=∠POD+∠AOB=60°+120°=180°，‎ 即P、O、B三点在同一直线上，‎ ‎∴y=2不符合题意，舍去，‎ ‎∴点P的坐标为（2，﹣2）‎ ‎②若OB=PB，则42+|y+2|2=42，‎ 解得y=﹣2，‎ 故点P的坐标为（2，﹣2），‎ ‎③若OP=BP，则22+|y|2=42+|y+2|2，‎ 解得y=﹣2，‎ 故点P的坐标为（2，﹣2），‎ 综上所述，符合条件的点P只有一个，其坐标为（2，﹣2），‎ ‎【2.2012菏泽】‎ ‎21．如图，在平面直角坐标系中放置一直角三角板，其顶点为A（0，1），B（2，0），O（0，0），将此三角板绕原点O逆时针旋转90°，得到△A′B′O．‎ ‎（1）一抛物线经过点A′、B′、B，求该抛物线的解析式；‎ ‎（2）设点P是在第一象限内抛物线上的一动点，是否存在点P，使四边形PB′A′B的面积是△A′B′O面积4倍？若存在，请求出P的坐标；若不存在，请说明理由．‎ ‎（3）在（2）的条件下，试指出四边形PB′A′B是哪种形状的四边形？并写出四边形PB′A′B的两条性质．‎ 考点：二次函数综合题。‎ 解答：解：（1）△A′B′O是由△ABO绕原点O逆时针旋转90°得到的，‎ 又A（0，1），B（2，0），O（0，0），‎ ‎∴A′（﹣1，0），B′（0，2）．‎ 设抛物线的解析式为：，‎ ‎∵抛物线经过点A′、B′、B，‎ ‎，解之得，‎ 满足条件的抛物线的解析式为.．‎ ‎（2）∵P为第一象限内抛物线上的一动点，‎ 设P（x，y），则x＞0，y＞0，P点坐标满足．‎ 连接PB，PO，PB′，‎ ‎. ‎ 假设四边形的面积是面积的倍，则 ‎，‎ 即，解之得，此时，即.‎ ‎∴存在点P（1，2），使四边形PB′A′B的面积是△A′B′O面积的4倍．‎ ‎（3）四边形PB′A′B为等腰梯形，答案不唯一，下面性质中的任意2个均可．‎ ‎①等腰梯形同一底上的两个内角相等；②等腰梯形对角线相等；‎ ‎③等腰梯形上底与下底平行；④等腰梯形两腰相等．‎ 或用符号表示：‎ ‎①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′；②PA′=B′B；③B′P∥A′B；④B′A′=PB．‎ ‎【3. 2012义乌市】‎ ‎24．如图1，已知直线y=kx与抛物线y=交于点A（3，6）．‎ ‎（1）求直线y=kx的解析式和线段OA的长度；‎ ‎（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；‎ ‎（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？‎ 考点：二次函数综合题。‎ 解答：解：（1）把点A（3，6）代入y=kx 得；‎ ‎∵6=3k，‎ ‎∴k=2，‎ ‎∴y=2x．（2012义乌市）‎ OA=．…（3分）‎ ‎（2）是一个定值，理由如下：‎ 如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H．‎ ‎①当QH与QM重合时，显然QG与QN重合，‎ 此时；‎ ‎②当QH与QM不重合时，‎ ‎∵QN⊥QM，QG⊥QH 不妨设点H，G分别在x、y轴的正半轴上，‎ ‎∴∠MQH=∠GQN，‎ 又∵∠QHM=∠QGN=90°‎ ‎∴△QHM∽△QGN…（5分），‎ ‎∴，‎ 当点P、Q在抛物线和直线上不同位置时，同理可得． …（7分）①①‎ ‎（3）如答图2，延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R ‎∵∠AOD=∠BAE，‎ ‎∴AF=OF，‎ ‎∴OC=AC=OA=‎ ‎∵∠ARO=∠FCO=90°，∠AOR=∠FOC，‎ ‎∴△AOR∽△FOC，‎ ‎∴，‎ ‎∴OF=，‎ ‎∴点F（，0），‎ 设点B（x，），‎ 过点B作BK⊥AR于点K，则△AKB∽△ARF，‎ ‎∴，‎ 即，‎ 解得x1=6，x2=3（舍去），‎ ‎∴点B（6，2），‎ ‎∴BK=6﹣3=3，AK=6﹣2=4，‎ ‎∴AB=5 …（8分）；‎ ‎（求AB也可采用下面的方法）‎ 设直线AF为y=kx+b（k≠0）把点A（3，6），点F（，0）代入得 k=，b=10，‎ ‎∴，‎ ‎∴，‎ ‎∴（舍去），，‎ ‎∴B（6，2），‎ ‎∴AB=5…（8分）‎ ‎（其它方法求出AB的长酌情给分）‎ 在△ABE与△OED中 ‎∵∠BAE=∠BED，‎ ‎∴∠ABE+∠AEB=∠DEO+∠AEB，‎ ‎∴∠ABE=∠DEO，‎ ‎∵∠BAE=∠EOD，‎ ‎∴△ABE∽△OED．…（9分）‎ 设OE=x，则AE=﹣x （），‎ 由△ABE∽△OED得，‎ ‎∴‎ ‎∴（）…（10分）‎ ‎∴顶点为（，）‎ 如答图3，当时，OE=x=，此时E点有1个；‎ 当时，任取一个m的值都对应着两个x值，此时E点有2个．‎ ‎∴当时，E点只有1个…（11分）‎ 当时，E点有2个…（12分）．‎ ‎【4.2012•杭州】‎ ‎22．在平面直角坐标系内，反比例函数和二次函数y=k（x2+x﹣1）的图象交于点A（1，k）和点B（﹣1，﹣k）．‎ ‎（1）当k=﹣2时，求反比例函数的解析式；‎ ‎（2）要使反比例函数和二次函数都是y随着x的增大而增大，求k应满足的条件以及x的取值范围；‎ ‎（3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．‎ 考点： 二次函数综合题。‎ 分析： （1）当k=﹣2时，即可求得点A的坐标，然后设反比例函数的解析式为：y=，利用待定系数法即可求得答案；‎ ‎（2）由反比例函数和二次函数都是y随着x的增大而增大，可得k＜0，又由二次函数y=k（x2+x﹣1）的对称轴为x=﹣，可得x＜﹣时，才能使得y随着x的增大而增大；‎ ‎（3）由△ABQ是以AB为斜边的直角三角形，A点与B点关于原点对称，利用直角三角形斜边上的中线等于斜边的一半，即可得OQ=OA=OB，又由Q（﹣， k），A（1，k），即可得=，继而求得答案．‎ 解答： 解：（1）当k=﹣2时，A（1，﹣2），‎ ‎∵A在反比例函数图象上，‎ ‎∴设反比例函数的解析式为：y=，‎ 代入A（1，﹣2）得：﹣2=，‎ 解得：m=﹣2，‎ ‎∴反比例函数的解析式为：y=﹣；‎ ‎（2）∵要使反比例函数和二次函数都是y随着x的增大而增大，‎ ‎∴k＜0，‎ ‎∵二次函数y=k（x2+x﹣1）=k（x+）2﹣k，的对称轴为：直线x=﹣，‎ 要使二次函数y=k（x2+x﹣1）满足上述条件，在k＜0的情况下，x必须在对称轴的左边，‎ 即x＜﹣时，才能使得y随着x的增大而增大，‎ ‎∴综上所述，k＜0且x＜﹣；‎ ‎（3）由（2）可得：Q（﹣， k），‎ ‎∵△ABQ是以AB为斜边的直角三角形，A点与B点关于原点对称，（如图是其中的一种情况）‎ ‎∴原点O平分AB，‎ ‎∴OQ=OA=OB，‎ 作AD⊥OC，QC⊥OC，‎ ‎∴OQ==，‎ ‎∵OA==，‎ ‎∴=，‎ 解得：k=±．‎ 点评： 此题考查了二次函数的性质、反比例函数的性质以及直角三角形的性质等知识．此题综合性较强，难度较大，注意掌握待定系数法求函数解析式，注意数形结合思想的应用．‎ ‎【5.2012•烟台】‎ ‎26．如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．‎ ‎（1）直接写出点A的坐标，并求出抛物线的解析式；‎ ‎（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？‎ ‎（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．‎ 考点： 二次函数综合题。‎ 分析： （1）根据矩形的性质可以写出点A得到坐标；由顶点A的坐标可设该抛物线的顶点式方程为y=a（x﹣1）2+4，然后将点C的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）；‎ ‎（2）利用待定系数法求得直线AC的方程y=﹣2x+6；由图形与坐标变换可以求得点P的坐标（1，4﹣t），据此可以求得点E的纵坐标，将其代入直线AC方程可以求得点E或点G的横坐标；然后结合抛物线方程、图形与坐标变换可以求得GE=4﹣、点A到GE的距离为，C到GE的距离为2﹣；最后根据三角形的面积公式可以求得 S△ACG=S△AEG+S△CEG=﹣（t﹣2）2+1，由二次函数的最值可以解得t=2时，S△ACG的最大值为1；‎ ‎（3）因为菱形是邻边相等的平行四边形，所以点H在直线EF上．‎ 解答： 解：（1）A（1，4）．…（1分）‎ 由题意知，可设抛物线解析式为y=a（x﹣1）2+4‎ ‎∵抛物线过点C（3，0），‎ ‎∴0=a（3﹣1）2+4，‎ 解得，a=﹣1，‎ ‎∴抛物线的解析式为y=﹣（x﹣1）2+4，即y=﹣x2+2x+3．…（2分）‎ ‎（2）∵A（1，4），C（3，0），‎ ‎∴可求直线AC的解析式为y=﹣2x+6．‎ ‎∵点P（1，4﹣t）．…（3分） ‎∴将y=4﹣t代入y=﹣2x+6中，解得点E的横坐标为x=1+．…（4分）‎ ‎∴点G的横坐标为1+，代入抛物线的解析式中，可求点G的纵坐标为4﹣．‎ ‎∴GE=（4﹣）﹣（4﹣t）=t﹣．…（5分）‎ 又点A到GE的距离为，C到GE的距离为2﹣，‎ 即S△ACG=S△AEG+S△CEG=•EG•+•EG（2﹣）‎ ‎=•2（t﹣）=﹣（t﹣2）2+1．…（7分）‎ 当t=2时，S△ACG的最大值为1．…（8分）‎ ‎（3）t=或t=20﹣8．…（12分）‎ ‎（说明：每值各占（2分），多出的值未舍去，每个扣1分）‎ 点评： 本题考查了二次函数的综合题．其中涉及到的知识点有待定系数法求二次函数的解析式，待定系数法求一次函数的解析式以及三角形面积的求法．‎ ‎【6.2012•益阳】‎ ‎20．已知：如图，抛物线y=a（x﹣1）2+c与x轴交于点A（，0）和点B，将抛物线沿x轴向上翻折，顶点P落在点P'（1，3）处．‎ ‎（1）求原抛物线的解析式；‎ ‎（2）学校举行班徽设计比赛，九年级5班的小明在解答此题时顿生灵感：过点P'作x轴的平行线交抛物线于C、D两点，将翻折后得到的新图象在直线CD以上的部分去掉，设计成一个“W”型的班徽，“5”的拼音开头字母为W，“W”图案似大鹏展翅，寓意深远；而且小明通过计算惊奇的发现这个“W”图案的高与宽（CD）的比非常接近黄金分割比（约等于0.618）．请你计算这个“W”图案的高与宽的比到底是多少？（参考数据：，，结果可保留根号）‎ 考点： 二次函数的应用。‎ 分析： （1）利用P与P′（1，3）关于x轴对称，得出P点坐标，利用待定系数法求出二次函数的解析式即可；‎ ‎（2）根据已知得出C，D两点坐标，进而得出“W”图案的高与宽（CD）的比．‎ 解答： 解：（1）∵P与P′（1，3）关于x轴对称，‎ ‎∴P点坐标为（1，﹣3）； …（2分）‎ ‎∵抛物线y=a（x﹣1）2+c过点A（，0），顶点是P（1，﹣3），‎ ‎∴；…（3分）‎ 解得；…（4分）‎ 则抛物线的解析式为y=（x﹣1）2﹣3，…（5分）‎ 即y=x2﹣2x﹣2．‎ ‎（2）∵CD平行x轴，P′（1，3）在CD上，‎ ‎∴C、D两点纵坐标为3； …（6分）‎ 由（x﹣1）2﹣3=3，‎ 解得：，，…（7分）‎ ‎∴C、D两点的坐标分别为（，3），（，3）‎ ‎∴CD=…（8分）‎ ‎∴“W”图案的高与宽（CD）的比=（或约等于0.6124）…（10分）．‎ 点评： 此题主要考查了待定系数法求二次函数的解析式以及二次函数的应用，根据已知得出C，D两点坐标是解题关键．‎ ‎【7.2012•广州】‎ ‎24．如图，抛物线y=与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．‎ ‎（1）求点A、B的坐标；‎ ‎（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；‎ ‎（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．‎ 考点： 二次函数综合题。‎ 分析： （1）A、B点为抛物线与x轴交点，令y=0，解一元二次方程即可求解．‎ ‎（2）根据题意求出△ACD中AC边上的高，设为h．在坐标平面内，作AC的平行线，平行线之间的距离等于h．根据等底等高面积相等的原理，则平行线与坐标轴的交点即为所求的D点．‎ 从一次函数的观点来看，这样的平行线可以看做是直线AC向上或向下平移而形成．因此先求出直线AC的解析式，再求出平移距离，即可求得所作平行线的解析式，从而求得D点坐标．‎ 注意：这样的平行线有两条，如答图1所示．‎ ‎（3）本问关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义．‎ 因为过A、B点作x轴的垂线，其与直线l的两个交点均可以与A、B点构成直角三角形，这样已经有符合题意的两个直角三角形；第三个直角三角形从直线与圆的位置关系方面考虑，以AB为直径作圆，当直线与圆相切时，根据圆周角定理，切点与A、B点构成直角三角形．从而问题得解．‎ 注意：这样的切线有两条，如答图2所示．‎ 解答： 解：（1）令y=0，即=0，‎ 解得x1=﹣4，x2=2，‎ ‎∴A、B点的坐标为A（﹣4，0）、B（2，0）．‎ ‎（2）S△ACB=AB•OC=9，‎ 在Rt△AOC中，AC===5，‎ 设△ACD中AC边上的高为h，则有AC•h=9，解得h=．‎ 如答图1，在坐标平面内作直线平行于AC，且到AC的距离=h=，这样的直线有2条，分别是l1和l2，则直线与对称轴x=﹣1的两个交点即为所求的点D．‎ 设l1交y轴于E，过C作CF⊥l1于F，则CF=h=，‎ ‎∴CE==．‎ 设直线AC的解析式为y=kx+b，将A（﹣4，0），B（0，3）坐标代入，‎ 得到，解得，∴直线AC解析式为y=x+3．‎ 直线l1可以看做直线AC向下平移CE长度单位（个长度单位）而形成的，‎ ‎∴直线l1的解析式为y=x+3﹣=x﹣．‎ 则D1的纵坐标为×（﹣1）﹣=，∴D1（﹣4，）．‎ 同理，直线AC向上平移个长度单位得到l2，可求得D2（﹣1，）‎ 综上所述，D点坐标为：D1（﹣4，），D2（﹣1，）．‎ ‎（3）如答图2，以AB为直径作⊙F，圆心为F．过E点作⊙F的切线，这样的切线有2条．‎ 连接FM，过M作MN⊥x轴于点N．‎ ‎∵A（﹣4，0），B（2，0），∴F（﹣1，0），⊙F半径FM=FB=3．‎ 又FE=5，则在Rt△MEF中，‎ ME==4，sin∠MFE=，cos∠MFE=．‎ 在Rt△FMN中，MN=MN•sin∠MFE=3×=，‎ FN=MN•cos∠MFE=3×=，则ON=，‎ ‎∴M点坐标为（，）‎ 直线l过M（，），E（4，0），‎ 设直线l的解析式为y=kx+b，则有 ‎，解得，‎ 所以直线l的解析式为y=x+3．‎ 同理，可以求得另一条切线的解析式为y=x﹣3．‎ 综上所述，直线l的解析式为y=x+3或y=x﹣3．‎ 点评： 本题解题关键是二次函数、一次函数以及圆等知识的综合运用．难点在于第（3）问中对于“以A、B、M为顶点所作的直角三角形有且只有三个”条件的理解，这可以从直线与圆的位置关系方面入手解决．本题难度较大，需要同学们对所学知识融会贯通、灵活运用．‎ ‎【8.2012•丽水】‎ ‎24．在△ABC中，∠ABC＝45°，tan∠ACB＝．如图，把△ABC的一边BC放置在x轴上，有OB＝14，OC＝，AC与y轴交于点E． ‎ ‎(1)求AC所在直线的函数解析式；‎ ‎(2)过点O作OG⊥AC，垂足为G，求△OEG的面积；‎ ‎(3)已知点F(10，0)，在△ABC的边上取两点P，Q，是否存在以O，P，Q为顶点的三角形与△OFP全等，且这两个三角形在OP的异侧？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．‎ 考点： 一次函数综合题。‎ 分析： (1)根据三角函数求E点坐标，运用待定系数法求解；‎ ‎(2)在Rt△OGE中，运用三角函数和勾股定理求EG，OG的长度，再计算面积；‎ ‎(3)分两种情况讨论求解：①点Q在AC上；②点Q在AB上．求直线OP与直线AC的交点坐标即可．‎ 解答： 解：(1)在Rt△OCE中，OE＝OCtan∠OCE＝＝，∴点E(0，2)．‎ 设直线AC的函数解析式为y＝kx＋，有，解得：k＝．‎ ‎∴直线AC的函数解析式为y＝．‎ ‎(2)在Rt△OGE中，tan∠EOG＝tan∠OCE＝＝，‎ 设EG＝3t，OG＝5t，OE＝＝t，∴，得t＝2，‎ 故EG＝6，OG＝10，‎ ‎∴S△OEG＝．‎ ‎(3)存在．‎ ‎①当点Q在AC上时，点Q即为点G，‎ 如图1，作∠FOQ的角平分线交CE于点P1，‎ 由△OP1F≌△OP1Q，则有P1F⊥x轴，由于点P1在直线AC上，当x＝10时，‎ y＝－＝，‎ ‎∴点P1(10，)．‎ ‎②当点Q在AB上时，‎ 如图2，有OQ＝OF，作∠FOQ的角平分线交CE于点P2，‎ 过点Q作QH⊥OB于点H，设OH＝a，‎ 则BH＝QH＝14－a，‎ 在Rt△OQH中，a2＋(14－a)2＝100，‎ 解得：a1＝6，a2＝8，‎ ‎∴Q(－6，8)或Q(－8，6)．‎ 连接QF交OP2于点M．‎ 当Q(－6，8)时，则点M(2，4)．‎ 当Q(－8，6)时，则点M(1，3)．‎ 设直线OP2的解析式为y＝kx，则 ‎2k＝4，k＝2．‎ ‎∴y＝2x．‎ 解方程组，得．‎ ‎∴P2()；‎ 当Q(－8，6)时，则点M(1，3)．‎ 同理可求P2′()．‎ 综上所述，满足条件的P点坐标为(10，)或()或()．‎ 点评： 此题考查一次函数的综合应用，运用了分类讨论的数学思想方法，综合性强，难度大．‎ ‎【9. 2012铜仁】‎ ‎25．如图，已知：直线交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c经过A、B、C（1，0）三点.‎ ‎（1）求抛物线的解析式;‎ ‎（2）若点D的坐标为（-1，0），在直线上有一点P,使ΔABO与ΔADP相似，求出点P的坐标；‎ ‎（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使ΔADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．‎ 考点：二次函数综合题。‎ 解答：解：（1）：由题意得，A（3，0），B（0，3）‎ ‎∵抛物线经过A、B、C三点，∴把A（3，0），B（0，3），C（1，0）三点分别代入得方程组 ‎ ‎ 解得：‎ ‎∴抛物线的解析式为 ‎ ‎（2）由题意可得：△ABO为等腰三角形,如图所示，‎ 若△ABO∽△AP1D，则 ‎∴DP1=AD=4 ,‎ ‎∴P1‎ 若△ABO∽△ADP2 ，过点P2作P2 M⊥x轴于M，AD=4, ‎ ‎∵△ABO为等腰三角形, ∴△ADP2是等腰三角形,由三线合一可得：DM=AM=2= P2M，即点M与点C重合∴P2（1，2）‎ ‎（3）如图设点E ，则 ‎ ‎①当P1(-1,4)时，‎ S四边形AP1CE=S三角形ACP1+S三角形ACE ‎ = ‎ ‎ ∴ ∴‎ ‎∵点E在x轴下方 ∴‎ 代入得： ,即 ‎ ‎∵△=(-4)2-4×7=-12<0‎ ‎∴此方程无解 ‎②当P2（1，2）时，S四边形AP2CE=S三角形ACP2+S三角形ACE = ‎ ‎ ∴ ∴‎ ‎∵点E在x轴下方 ∴ 代入得：‎ 即 ，∵△=(-4)2-4×5=-4<0‎ ‎∴此方程无解 综上所述，在x轴下方的抛物线上不存在这样的点E。‎ ‎【10. 2012泰安】‎ ‎29．如图，半径为2的⊙C与x轴的正半轴交于点A，与y轴的正半轴交于点B，点C的坐标为（1，0）．若抛物线过A、B两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上是否存在点P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；‎ ‎（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值．‎ 考点：二次函数综合题。‎ 解答：解：（1）如答图1，连接OB．‎ ‎∵BC=2，OC=1‎ ‎∴OB=‎ ‎∴B（0，）‎ 将A（3，0），B（0，）代入二次函数的表达式 得 ，解得： ，‎ ‎∴．初中数学黄金资源网 ‎（2）存在．‎ 如答图2，作线段OB的垂直平分线l，与抛物线的交点即为点P．‎ ‎∵B（0，），O（0，0），‎ ‎∴直线l的表达式为．代入抛物线的表达式，‎ 得；‎ 解得，‎ ‎∴P（）．‎ ‎（3）如答图3，作MH⊥x轴于点H．‎ 设M（ ），‎ 则S△MAB=S梯形MBOH+S△MHA﹣S△OAB=（MH+OB）•OH+HA•MH﹣OA•OB ‎=‎ ‎= ‎ ‎∵，‎ ‎∴ ‎ ‎= ‎ ‎∴当时，取得最大值，最大值为．初中数学黄金资源网