中考数学猜想规律与探索押轴题专练

中考数学猜想规律与探索押轴题专练

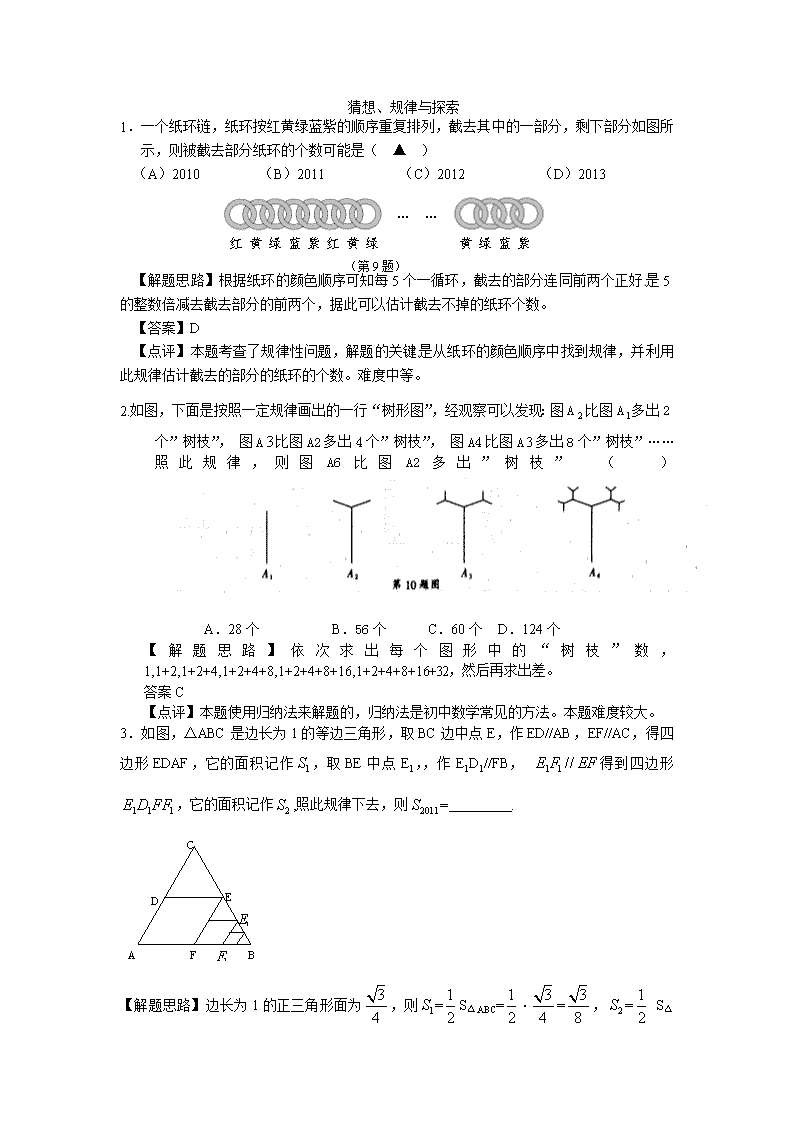
猜想、规律与探索 1．一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所 示，则被截去部分纸环的个数可能是（　▲　） （A）2010 （B）2011 （C）2012 （D）2013 【解题思路】根据纸环的颜色顺序可知每 5 个一循环，截去的部分连同前两个正好 是 5 的整数倍减去截去部分的前两个，据此可以估计截去不掉的纸环个数。 【答案】D 【点评】本题考查了规律性问题，解题的关键 是从纸环的颜色顺序中找到规律，并利用 此规律估计截去的部分的纸环的个数。难度中等。 2.如图，下面是按照一定规律画出的一行“树形图”，经观察可以发现：图 A 比图 A 多出 2 个”树枝”， 图 A 比图 A2 多出 4 个”树枝”， 图 A4 比图 A 多出 8 个”树枝”…… 照 此 规 律 ， 则 图 A6 比 图 A2 多 出 ” 树 枝 ” （ ） A．28 个 B．56 个 C．60 个 D．124 个 【 解 题 思 路 】 依 次 求 出 每 个 图 形 中 的 “ 树 枝 ” 数 ， 1,1+2,1+2+4,1+2+4+8,1+2+4+8+16,1+2+4+8+16+32，然后再求出差。 答案 C 【点评】本题使用归纳法来解题的，归纳法是初中数学常见的方法。本题难度较大。 3．如图，△ABC 是边长为 1 的等边三角形，取 BC 边中点 E，作 ED//AB，EF//AC，得四 边形 EDAF，它的面积记作 ，取 BE 中点 E1，，作 E1D1//FB， 得到四边形 ，它的面积记作 ,照此规律下去，则 = . 【解题思路】边长为 1 的正三角形面为 ，则 = S△ABC= · = ， = S△ 2 1 3 3 1S 1 1 //E F EF 1 1 1E D FF 2S 2011S A B D C E F 1F 1E 3 4 1S 1 2 1 2 3 4 3 8 2S 1 2 （第 9 题） … … 红 黄 绿 蓝 紫 红 黄 绿 黄 绿 蓝 紫 EFB= · S△ABC= · ，…， = · . 【答案】 · 或 · 【点评】本题为规律探索题，主要考查观察、类比、归纳的能力。解题思路：从特殊情形入 手——探索发现规律——猜想结论——验证.难度较大. 4、如图是用相同长度的小棒摆成的一组有规律的图案，图案（1）需要 4 根小棒，图案（2） 需要 10 根小棒……，按此规律摆下去，第 n 个图案需要小棒 根（用含有 n 的代数式表示）。 【解 题思路】由图形可知每个后面的图形都比前一个图形多 6 各小棒，图案（1）有 4 个， 图案（2）有 4+6，图案（3）有 4+6×2……，图案（3）有 4+6（n﹣1）=6n﹣2 【答案】6n﹣2 【点评】本题主要考察观察图形探索规律，此题的关键在于认真观察图形从中寻找规律，然 后用代数式表示出来。难度较小。 5．如图 9，给正五边形的顶点依次编号为 1，2，3，4，5.若从某一顶点开始，沿正 五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一 次“移位”. 如：小宇在编号为 3 的顶点时，那么他应走 3 个边长，即从 3→4→5→1 为第一次 “移位”，这时他到达编号为 1 的顶点；然后从 1→2 为第二次“移位”. 若小宇从编号为 2 的顶点开始，第 10 次“移位”后，则他所处顶点的编号是 ____________. 【分析与解】根据示例，从 2 开始移位，不难发现 4 次移位之后，又回到出发点，即 确定第 10 次移位后的位置即确定第二次移位后的位置即可，第一次移位到达 4，第二次移 位到达 3，故 10 次“移位”后，则他所处顶点的编号是 3． 【点评】本题属于中等题，为循环规律题，弄清题意，确定几次循环即可解题. 6．）若 ， ， ，… ；则 的值为 ．（用含 的代数式表示） 【 解 题 思 路 】 把 化 简 后 可 得 规 律 【答案】 【点评】本题考查分式的化简计算及规律的寻找，难度中等． 7．如图，用围棋子按下面的规律摆图形，则摆第 n 个图形需要围棋子的枚数为（ ）． 1 2 1 4 3 8 1 4 2011S 3 8 20101( )4 3 8 20101( )4 40231( )2 3 1 11a m = − 2 1 11a a = − 3 2 11a a = − 2011a m 2 3 4 5a a a a、 、 、 1 2 3 4 5 6 1 1 1 11 11 1a a a m a a a mm m m m = − = − = = − = − =− − 、 、 、 、 、 11 m − 1 2 34 5 图 9 A． B． C． D． 【解题思路】由图形可知，第一个用围棋子的枚数为 ；第二个用围棋子的枚数为 ；第三个用围棋子的枚数为 ，所以根据规律，可知第 n 个图形 需要围棋子的枚数为 。 【答案】C 【点评】本题属于规律探索题，解决的关键是根据图形变化的痕迹找到规律，从而用含有 的代数式表示出来。 8 如图，观察每一个图中黑色正六边形的排列规律，则第 10 个图中黑色正六边形有 个。 【解题思路】数一下每个图的黑色正六边形的个数：第一个图 1 个；第二个图 4 个；第三 个图 9 个，1=12、4=22、9=32 猜想：第 10 个图中黑色正六边形有 102=100 个 【答案】100 【点评】此题属于探索规律型题目，解题关键是 抓住图形序数与黑色正六边形的个数之间的规 律，如此题的是序数的平方。难度中等。 9．观察上面的图形，它们是按一定规律排列的，依照此规律，第_____个图形共有 120 个 ★． 【解题思路】第 1 个图形有 1 个★，第 2 个图形有 3 个★，且 3＝1+2＝ ，第 3 个 图 形 有 6 个 ★ ， 且 6 ＝ 1+2+3= ， 第 4 个 图 形 有 10 个 ★ ， 且 10 ＝ 1+2+3+4= ．则第 n 个图形有 120 个★，则第 n 个图形中★的个数是 1+2+3+…+n＝ ，即 ＝120，整理，得 n2+n－240＝0．解方程，得 n1＝15，n2＝－16(不合 舍去)．所以，第 15 个图形有 120 个★． 【答案】15 【点评】根据简单图形★的个数，找出图形★的个数与图形序号之间的关系，然后用代 n5 15 −n 16 −n 12 2 +n 5 16511 ×+= 26517 ×+= 16165 −=−+ nn ）（ n 2(2+1) 2 3(3+1) 2 4(4+1) 2 ( +1) 2 n n ( +1) 2 n n 数式表示． 10．如图 4 所示，直线 OP 经过点 P(4, )，过 x 轴上的点 l、3、5、7、9、11……分别 作 x 轴的垂线，与直线 OP 相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为 S1、S2、S3……Sn 则 Sn 关于 n 的函数关系式是____ 【解题思路】先求出直线 op 解析式为：y= 经观察可知每个小梯形的高一定为 2， 面积为 Sn 的梯形上底所在直线为 x=4n-3，上底长为 ，下底所在直线为 x=4n-1，上底长为 ，故梯形的面积 Sn= (8n－4) 【答案】 (8n－4) 【点评】本题为探究规律试题，具有一定的难度。 11、如图（9），已知∠AOB= ，在射线 OA、OB 上分别取点 OA =OB ，连结 A B ， 在 B A 、B B 上分别取点 A 、B ，使 B B = B A ，连结 A B …按此规律上 去，记∠A B B = ，∠ ，…，∠ 则（1） = ； = 。 【解题思路】：根据题意：OA1=OB1，△A1OB1，△A2B1B2，△A3B2B3……是等腰三角形， 已知∠AOB= ，∴ =1800- = ;以此类推可得：=1800-（900- ）…… = 4 3 0 1 3 5 7 9 11 S1 S2 S3 图 4 x y p 3x 3(4n 3)− 3(4n 1)− 3 3 α 1 1 1 1 1 1 1 2 2 1 2 1 2 2 2 2 1 2 1 θ 3 2 3 2A B B θ= n+1 1A n n nB B θ+ = 1 θ n θ α 1 θ 2 1800 ∂− 2 1800 ∂+ 4 1800 ∂− n θ 。 【答案】 ； 。 【点评】本题是规律探究性问题，是中考的热点问题之一，在已知等腰三角形的顶角的情况 下，通过计算三角形的外角来探索规律。本题难度中等。 12． 在直角坐标中，正方形 A1B1C1O1、A2B2C2C1、A3B3C3C2、、、、、、AnBnCnCn-1 按如图所 示的方式放置，其中点 A1、A2、A3、、、、、An 均在一次函数 y=kx+b 上，点 C 1、C2、C 3、、、、、 Cn 均在 x 轴上.若点,B 1 的坐标为（1,1），点 B 2 的坐标为（3,2），则点 An 的坐标 为　　　　　　. 【思路分析】解：由 B1 的坐标为（1,1），点 B2 的坐标为（3,2），知 A1（0,1）， A2 （1,2），设直线解析式 y=kx+b,把 A1（0,1）， A2（1,2）代入上式得， ，∴ k=1,b=2,∴y＝x＋1． ∵点 B2 的坐标为（3,2），∴C2 的坐标为（3,0），把 x=3 代入 y＝x＋1 得 y=4,∴A3 的 坐标为（3,4），同理得 A4 的坐标为（7,8），A5 的坐标为（15,16）………An 的坐标为(2n－1 －1, 2n－1) ． n n 2 180)12( 0 ∂+×− 2 1800 ∂+ n n 2 180)12( 0 ∂+×− y=kx+b O A1 A2 A3 B3 B2 B1 C1 C2 C3 x y    += = bk b 2 1 【答案】(2n－1－1, 2n－1) ． 【点评】解答这类问题首先根据点在图像上求出前几个点的坐标，然后根据所出现的 规律找到相应的公式，然后对公式进行验证． 13．如图(1)，将一个正六边形各边延长，构成一个正六角星形 AFBDCE，它的面积为 1；取 △ABC 和△DEF 各边中点，连接成正六角星形 A1F1B1D1C1E1，如图(2)中阴影部分；取△A1B1C1 和△D1E1F1 各边中点，连接成正六角星形 A2F2B2D2C2E2，如图(3)中阴影部分；如此下去…， 则正六角星形 A4F4B4D4C4E4 的面积为_________________． 【解题思路】由三角形中位线性质得：A1B1：AB= 1：2，即 A1B1= AB，同理可得 A2B2= A1B1= AB；A3B3= A2B2= AB；A4B4= A3B3= AB，即第四个正六角星形与第一个正六 角星形的边长之比为 1：16，根据“相似多边形面积比等于相似比的平方”知它们的面积比 为 1：256 ，所以正六角星形 A4F4B4D4C4E4 的面积= ×正六角星形 AFBDCE 的面积= . 【答案】 【点评】本题考查从图形中探索数的规律问题.只要想到从相似多边形性质去考虑，问题将 容易得解. 难度中等 14．一个平面封闭图形内（含边界）任意两点距离的最大值称为该图形的“直径”，封闭图 形的周长与直径之比称为图形的“周率”，下面四个平面图形（依次为正三角形、正方形、 正六边形、圆）的周率从左到右依次记为 ， ， ， ，则下列关系中正确的是 （A） > > （B） > > （C） > > （D） > > 【解题思路】根据新规定，设第一个图形的边长为 1，其周长为 3，直径为 1，所以 =3， 1 2 1 2 21( )2 1 2 31( )2 1 2 41( )2 1 256 1 256 1 256 1a 2a 3a 4a 4a 2a 1a 4a 3a 2a 1a 2a 3a 2a 3a 4a 1a 题 10 图（1） A1 B C D A F E B C D A F E B C D A F E B1 C1 F1 D1 E1 A1 B1 C1 F1 D1 E1A2 B2 C2 F2 D2 E2 题 10 图（2） 题 10 图（3） 设第二个图形的边长为 1，其周长为 4，直径为 ，所以 =2 ， 设第三个图形的边长为 1，其周长为 6，直径为 2，所以 =3，第三个图形的周长与直径之 比为 ，所以 > > ，故选 B． 【答案】B 【点评】本题是图形的规律探究题，实质就是图形边长的规律探究．本题可先计算，再比较 大小，本题还带有自主学习的成分，培养学生的自主学习能力应成为今后教学的重点，属于 中档题． 15． 观察图中正方形四个顶点所标的数字规律，可知数 2011 应标在 （A）第 502 个正方形的左下角　　　（B）第 502 个正方形的右下角 （C）第 503 个正方形的左上角　　　（D）第 503 个正方形的右下角 【解题思路】有图形可以确定数字每四个一个循环，所以 2011÷4=502……3，所以第 503 个的左上角，答案选 C 【答案】C 【点评】规律性探究问题通常指根据给出的材料，观察其中的规律，再运用这种规律解决问 题的一类题型. 观察的三种主要途径：（1）、式与数的特征观察；（2）、图形的结构观察； （3）、通过对简单、特殊 情况的观察，再推广到一般情况。规律探究的基本原则：（1）、 遵循类推原则，项找项的规律，和找和的规律，差找差的规律，积找积的规律。（2）、遵循 有序原则，从特殊开始，从简单开始，先找 3 个，发现规律，再验证运用规律. 16．图 1 是一个边长为 1 的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长 的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图 2），依此规律 继续拼下去（如图 3），……，则第 n 个图形的周长是 （A） （B） （C） （D） 【解题思路】先由已知条件分别算出图形 1 的周长为 4=21+1，图形,2 的周长为 8=22+1，以此 类推，图形 n 的周长为 2n+1，故选 C． 2 2a 2 3a π 4a 3a 2a 2n 4n 12n+ 22n+ 16 图 1 图 2 图 3 …… 【答案】C 【点评】本题属于找规律的问题，属于中等题目，在解答本题时，需要先进行归纳推理，由 特殊到一般的推理，然后得出一般性的结论即可． 17.（山东临沂 第 19 题3 分）如图，上面各图都是用全等三角形拼成的一组图形，则在第 10 个这样的图形中，共有 个等腰梯形。 …… (1) (2) (3) 解题思路：第（1）个图形由三个全等三角形组成，有 1=12 个等腰梯形；第（2）个图形由 五个全等三角形组成，有 4=22 个等腰梯形；第（3）个图形由七个全等三角形组成，有 9=32 个等腰梯形；……，第 10 个这样的图形中，共有 102=100 个等腰梯形. 解答：填 100. 点评：这是一道规律性探索题，解答本题的关键是找到第 n 个图形中，等腰梯形的个数与 n 之间的平方关系，这也是本题的难点所在.本题难度较大. 18.填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m 的值是 . 【解题思路】由规律可知，最后一个图形左下那个数为 12，右上那个数为 14；另外一个规 律是这两个数的乘积正好等于 10 与 m 的和。 【答案】158 【点评】规律探求型问题一直中考中的热门试题，在处理此类问题时，关键要找出问题中所 蕴含的规律，然后加以运用。难度较大。 20 如下数表是由从 1 开始的连续自然数 组成，观察规律并完成各题的解答． 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 ………………………… （1）表中第 8 行的最后一个数是______________，它是自然数_____________的平方，第 8 行共有____________个数； （2）用含 n 的代数式表示：第 n 行的第一个数是___________________，最后一个数是 （第 14 题图） ________________，第 n 行共有_______________个数； （3）求第 n 行各数之和． 【解题思路】认真阅读，发现上述规律，每行的最后的一个数式行数的平方，便可解答了。 【答案】(1)64，8，15； （2）n2-2n+2，n2，(2n-1); （3）第 n 行各数之和： 【点评】规律探究题是近几年中考的热点，本题还带有自主学习的成分，培养学生的自主学 习能力应成为今后教学的重点，属于中档题． 21． (本题满分 10 分) （2011 山东德州，22，10 分）●观察计算 当 ， 时， 与 的大小关系是_________________． 当 ， 时， 与 的大小关系是_________________． ●探究证明 如 图 所 示 ， 为 圆 O 的 内 接 三 角 形 ， 为 直 径 ， 过 C 作 于 D ， 设 ，BD=b． （1）分别用 表示线段 OC，CD； （2）探求 OC 与 CD 表达式之间存在的关系 （用含 a，b 的式子表示）． ●归纳结论 根 据 上 面 的 观 察 计 算 、 探 究 证 明 ， 你 能 得 出 与 的 大 小 关 系 是 ： _________________________． ●实践应用 要制作面积为 1 平方米的长方形镜框，直接利用探究得出的结论，求出镜框周长的最小 值． 【解题思路】题属于推理应用题，要把握住最基本问题的思路，由此为切入点，结合图形性 质找到问题的突破口． 【答案】（1） ，∴ ， AB 为⊙O 直径, ∴ . ， ， ∴∠A=∠BCD.∴△ ∽△ . ∴ .即 ,∴ . （2）当 时, , = ； 时, , > ． )12)(1()12(2 22 2 22 −+−=−×++− nnnnnnn 5a = 3b = 2 a b+ ab 4a = 4b = 2 a b+ ab ABC∆ AB CD AB⊥ AD a= ,a b 2 a b+ ab 2AB AD BD OC= + = 2 a bOC +=  90ACB∠ = ° 90A ACD∠ + ∠ = ° 90ACD BCD∠ + ∠ = ° ACD CBD AD CD CD BD = 2CD AD BD ab= ⋅ = CD ab= a b= OC CD= 2 a b+ ab a b≠ OC CD> 2 a b+ ab A B C O D ●结论归纳: ． ●实践应用：设长方形一边长为 米,则另一边长为 米,设镜框周长为 l 米，则 ≥ ． 当 ,即 （米）时,镜框周长最小．此时四边形为 正方形时,周长最小为 4 米. 【点评】此类探究题是中考中的热门考点，综合性很强，考察同学们自主探究和应用创新的 能力，本题设计数学实践活动情景，问题由特殊到一般，在考查基础知识综合应用的同时， 兼顾考查学生知识转化能力，作图能力以及实践操作能力，符合新课改精神，是一道不可多 得的好题． 22．（2011 四川乐山，25，12 分）如图（14.1）,在直角△ABC 中, ∠ACB=90 ,CD⊥AB,垂 足为 D,点 E 在 AC 上,BE 交 CD 于点 G,EF⊥BE 交 AB 于点 F,若 AC=mBC,CE=nEA(m,n 为 实数). 试探究线段 EF 与 EG 的数量关系. (1) 如图(14.2),当 m=1,n=1 时,EF 与 EG 的数量关系是 证明: (2) 如图(14.3),当 m=1,n 为任意实数时,EF 与 EG 的数量关系是 证明 (3) 如图(14.1),当 m,n 均为任意实数时,EF 与 EG 的数量关系是 (写出关系式,不必证明) 【解题思路】：添加辅助线，构建新的直角三角形，推理证明三角形相似，利用相似关系， 列比例式推出 EF 与 EG 的数量关系。 【答案】(1)相等。如,14.2，当 m=1,n=1 时,△ACB 是等腰直角三角形，E 为 AC 中点，作 EM ⊥AB,EN⊥CD,垂足分别为 M、N，EM、EN 为中位线，∴△EFM≌△ENG,∴EF=EG. （2）EF:EG=1：n。作 EM⊥AB,EN⊥CD,垂足分别为 M、N，m=1, △ACB 是等腰直角 三角形，△EFM∽△ENG,∴EF:EG=EM:EN=AE:EC,∴EF:EG=AE:nAE=1:n. 【点评】本题是属于图形演变、规律探索性题目，找准基础图形，作出辅助线，确定三角形 全等或相似关系，列出关系式，是解题的关键。本题难度较大。 2 a b+ ≥ ab x 1 x 12( )l x x = + 14 4x x ⋅ = 1x x = 1x =  23．（本小题满分 10 分） 如图 14-①至图 14④中，两平行线 AB、CD 音的距离均为 6，点 M 为 AB 上一定点. 思考： 如图 14-①中，圆心为 O 的半圆形纸片在 AB、CD 之间（包括 AB、CD）， 其直径 MN 在 AB 上，MN＝8，点 P 为半圆上一点，设∠MOP＝α，当 α＝ ________度时，点 P 到 CD 的距离最小，最小值为________ ____. 探究一 在图 14-①的基础上，以点 M 为旋转中心，在 AB、CD 之间顺时针旋转该 半圆形纸片，直到不能再转动为止.如图 14-②，得到最大旋转角∠BMO＝ _______度，此时点 N 到 CD 的距离是______________. 探究二 将图 14-①中的扇形纸片 NOP 按下面对 α 的要求剪掉，使扇形纸片 MOP 绕 点 M 在 AB、CD 之间顺时针旋转. （1）如图 14-③，当 α＝60°时，求在旋转过程中，点 P 到 CD 的最小距离， 并请指出旋转角∠BMO 的最大值； （2）如图 14-④，在扇形纸片 MOP 旋转过程中，要保证点 P 能落在直线 CD 上，请确定 α 的取值范围. （参考数据：sin49°＝ 3 4，cos41°＝ 3 4，tan37°＝ 3 4） 【分析与解】思考：点 P 的位置越低，P 点到直线 CD 的距离越短，故当 α＝90°时，点 P 到 CD 的距离最小；探究一：当半圆形纸片不能再转动时， 半圆形纸片与 CD 相切，过切点，连半径后易得∠BMO＝30°；探究二： （1）须画出 α＝60°时的图形，利用圆、三角函数等相关知识可轻松解 题；（2）是本题的难点，须画出点 P 能落在直线 CD 上时的临界图形即 可确定 α 的取值范围. 解：思考 90，2. 探究一 30，2. 探究二 （1）由已知得 M 与 P 的距离为 4，∴当 MP⊥AB 时，点 P 到 AB 的最大距离是 4，从而点 P 到 CD 的最小距离为 6－4＝2. 当扇形 MOP 在 AB，CD 之间旋转到不能再转时，M P⌒ 与 AB 相切，此时旋转角最大，∠BMO 的最大值为 90°. （2）如图 4，由探究一可知，点 P 是M P⌒ 与 CD 的切点时，α 达到最大，即 OP⊥CD.此时， 延长 PO 交 AB 于点 H，α 最大值为∠OMH＋∠OHM＝30°＋90°＝120°. 如图 5，当点 P 在 CD 上且与 AB 距离最小时，MP⊥CD，α 达到最小，连接 MP，作 OH⊥MP 于点 H，由垂径定理，得 MH＝3，在 Rt△MOH 中，MO＝4， ∴sin∠MOH＝ M H OM ＝ 3 4，∴∠MOH＝49°，∵α＝2∠MOH，∴α 最小为 98°. ∴α 的取值范围是 98°≤α≤120°. BA DC 6 图 14-① α P OM N BA DC 6 图 14-② O P M N BA DC 6 图 14-③ O P M α BA DC 6 图 14-④ O P M α BA DC 6O P M αH BA DC 6O P M α H 【点评】本题属于较难题，为圆的探究题，以生活中的扇面为背景，通过扇面的展开与旋转 让同学们探究其中蕴含的数学知识，层层深入，环环相扣，最后一问最难，理解题意确定临 界位置是解题的关键，值得注意的是河北省今年将其放入倒数第二个压轴题目，可见圆在河 北省中考中的位置越来越重要. 24．(本小题满分 12 分) 如图 15，在平面直角坐标系中，点 P 从原点 O 出发，沿 x 轴向右以每秒 1 个单位长的速度 运动 t（t＞0）秒，抛物线 y＝x 2＋bx＋c 经过点 O 和点 P.已知矩形 ABCD 的三个顶点为 A （1，0）、B（1，－5）、D（4，0）. （1）求 c、b（用含 t 的代数式表示）； （2）当 4＜t＜5 时，设抛物线分别与线段 AB、CD 交于点 M、N. ①在点 P 的运动过程中，你认为∠AMP 的大小是否会变化？若变化， 说明理由；若不变，求出∠AMP 的值； ②求△MPN 的面积 S 与 t 的函数关系式，并求 t 为何值时，S＝21 8 ； （3）在矩形 ABCD 的内部（不含边界），把横、纵坐标都是整数的点称 为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接 写出 t 的取值范围. 【分析与解】（1）观察图像，可发现抛物线 y＝x2＋bx＋c 经过点 O 和点 P.故分别将 O 和点 P 代入解析式可用用含 t 的代数式表示 c、b；（2）△ AMP 为 Rt△，若∠AMP 不变，说明AP AM的值不变，故可求其比值即可确 定∠AMP 的值；（3）为数形结合，合理推理，借助网格直观性及抛物线的对称性可定 t 的取 值范围. 解：（1）把 x＝0，y＝0 代入 y＝x2＋bx＋c，得 c＝0. 再把 x＝t，y＝0 代入 y＝x2＋bx，得 t2＋bt＝0，∵t＞0，∴b＝－t. （2）①不变. 如图，当 x＝1 时，y＝1－t，故 M(1,1－t). ∵tan∠AMP＝1.∴∠AMP＝45°. ②S＝S 四边形 AMNP－S△PAM ＝S△DPN ＋S 梯形 NDAM－S△PAM ＝ 1 2(t－4)(4t－16)＋ 1 2[(4t－16)＋(t－1)]×3－ 1 2(t－1)(t－1) ＝ 3 2t2－ 15 2 t＋6 令 S＝ 21 8 ，得 3 2t2－ 15 2 t＋6＝ 21 8 ，得 t1＝ 1 2，t2＝ 9 2. ∵4＜t＜5，∴t1＝ 1 2舍去，∴t＝ 9 2. （3）7 2＜t＜11 3 理由：当 y＝x2－tx，经过点（2，－3）时，“好点” （2，－2）和（2，－ 1）在抛物线上方，此时－3＝22－2t，∴t＝7 2，当 x＝3 时，y＝－3 2，在－1 和－2 之间，说明“好点”（3，－1）也在抛物线上方.因此抛物线要将这些 “好点”分成数量相等的两部分时，必须 t＞7 2，如图，当 y＝x2－tx，经过 点（3，－2）时，“好点”（3，－1）在抛物线上方，此时－2＝32－3t，t＝ A D P O －1 M N CB x y 1 图 15 A D P O －1 M N CB x y 1 A D O －1 B x y C 11 3 ，当 x＝2 时，y＝－10 3 ，在－3 和－4 之间，说明“好点”（2，－3），（2，－2）（2，－1）也在 抛物线上方.因此抛物线要将这些“好点”分成数量相等的两部分时，必须 t＜11 3 . 【点评】河北省的压轴题目多年一直为几何动态综合题，今年突破为二次 函数与几何图形 动态综合题，是本卷的亮点所在，值得关注.问题设置由浅入深，上手容易，深入难，由其 是最后一问题更是新颖别致、独具匠心. 25、如图（1），RT△ABC 中，∠ABC=90°，CD⊥AB，垂足为 D，AF 平分∠CAB，交 CD 于点 E，交 CB 于点 F。 （1）求证：CE=CF （2）将图（2）中的△ADE 沿 AB 向右平移到△A`D`E`的位置，使点 E`落在 BC 边上，其 他条件不变，如图（2）所示请猜想：BE`与 CF 有怎样的数量 关系？请证明你的结论。 【解题思路】（1）要证 CE=CF 只需∠CFA=∠CEF 即可，由题 意可知∠CAF+∠CFA=90°，∠EAD+∠AED=90°，∠AED=∠ CEF 故可得∠CFA=∠CEF。（2）通过观察我们可知 BE`= CF，由（1）可知 CE=CF，要证 BE`= CF 只需 CE=BE`即可，过点 E 作 EG⊥AC 于 G，易证 RT△CEG≌RT△B E` D`，所以 CE=BE`。 【答案】（1）证明：∵AF 平分∠CAB，∴∠CAF=∠EAD ∵∠ABC=90°，∴∠CAF+∠CFA=90° 又∵CD⊥AB 于 D，∠EAD+∠AED=90°所以∠CFA=∠AED。 又∵∠AED=∠CEF，∴∠CFA=∠CEF ∴CE=CF。 （2）解：BE`= CF，证明如下 证明：如图过点 E 作 EG⊥AC 于 G， 又∵AF 平分∠CAB，ED⊥AB 所以 ED=EG 由平移性质可知：D`E`=DE，∴D`E`= EG 又∵∠ABC=90°，∴∠ACD+∠DCB=90° ∵CD⊥AB 于 D，∠B+∠DCB=90° ∴∠ACD=∠B 在 RT△CEG 和 RT△B E` D`中 ∴RT△CEG≌RT△B E` D` ∴CE=BE` 由（1）可知 CE=CF，∴BE`= CF 【点评】本题主要考察几何证明，涉及到直角三角形的性质、角平分线的定义、等角的余角 相等、三角形全等、等腰三角形的判定等内容。做此题的关键在于对图形的认真分析，可能    = ∠=∠ ∠=∠ D`E`GE BD`E`CGE BGCE 会出现不知如何作辅助线导致做题失败。难度中等。 26. △ABC 是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2， （1）要在这个正方形纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图 1）,比 较甲、乙两种剪法，哪种剪法所得的正方形面积更大？请说明理由. （2）图 1 中甲中剪称为第 1 次剪取，记所得正方形面积为 S1；按照甲种剪法，在余下的△ ADE 和△BDF 中，分别剪取正方形，得到两个相同的正方形，称为第 2 次剪取，并记这两 个正方形面积和为 S2（如图 2）,则 S2=______；再在余下的四个三角形中，用同样的方法分 别剪取正方形，得到四个相同的正方形，称为第 3 次剪取，并记这四个正方形的面积和为 S3 （如图 3）;继续操作下去…，则第 10 次剪取时，S10=___________. 【解题思路】（1）要想比较两个正方形的面积大小，可以通过等腰直角三角形的性质，计算 两个正方形的边长，因为正方形的面积等于边长的平方，所以只需要比较边长的即可.（2） 可以发现第二次剪取后所剩余的面积等于 ，第三次减取后所剩余的面积为 ，依 次发现规律即可. 【答案】(1)解法 1.如图甲，由题意，得 AE=DE=EC，即 EC=1，S 正方形 CFDE=12=1. 如图乙，设 MN=x,则由题意得 AM=MQ=PN=NB=MN=x ∴3x= ,解得，x= ,∴S 正方形 PNMQ= ， 又∵1> ∴甲种剪法所得的正方形的面积更大. 说明：图甲可另解为：由题意得点 D、E、F 分别为 AB、AC、BC 的中点，∴S 正方形 CFDE= S△ABC=1. 解法 2. 如图甲，由题意得，AE=DE=EC，即 EC=1 如图乙，设 MN=x,则由题意得 AM=MQ=PN=NB=MN=x 2 1 4 1 2 1 13 =− 22 3 22 9 8)3 22( 2 = 9 8 2 1 ∴3x= ,解得，x= 又∵1> ,即 EC>MN 所以甲种剪法所得的正方形面积更大. （1） S2= S10= (3)解法 1：探索规律可知：Sn= ， 剩余三角形的面积为： 2-（S1+S2+……S10）= = 解法 2：由题意可知： 第一次剪取后剩余三角形面积和为 2-S1=S1 第二次剪取后剩余三角形面积和为 S1-S2=1- = =S2 第三次剪取后剩余三角形的面积和为 S2-S3= - = =S3 …… 第十次剪取后剩余三角形的面积和为 S9-S10=S10= 【点评】本题考查了正方形的面积计算，以及等腰直角三角形的性质，在探索规律的时候应 该多列几个式子，从一般的推导中慢慢发现规律所在.难度中等. 22 3 22 3 22 2 1 n2 1 12 1 −n )2 1........4 1 2 11(2 9 ++++− 92 1 2 1 2 1 2 1 4 1 4 1 92 1