中考数学二模试卷1含解析

中考数学二模试卷1含解析

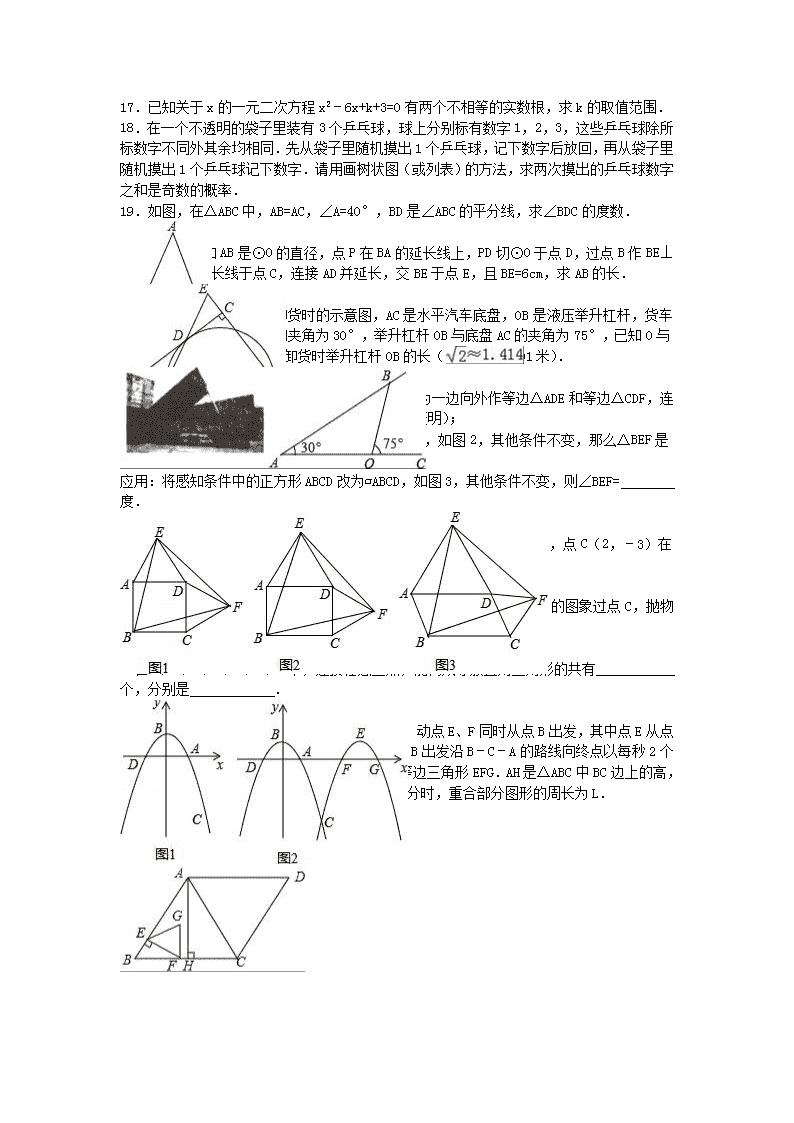
‎2016年吉林省长春市名校调研中考数学二模试卷 一、选择题：每小题3分，共24分．‎ ‎1．在实数﹣2，0，2，3中，最小的实数是（　　）‎ A．﹣2 B．0 C．2 D．3‎ ‎2．下列图形既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎3．如图，a∥b，将三角尺的直角顶点放在直线a上，若∠1=50°，则∠2的度数为（　　）‎ A．30° B．40° C．50° D．60°‎ ‎4．若一个正n边形的每个内角为156°，则这个正n边形的边数是（　　）‎ A．13 B．14 C．15 D．16‎ ‎5．已知关于x的方程2x+a﹣9=0的解是x=2，则a的值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎6．不等式组的解在数轴上表示为（　　）‎ A． B． C． D．‎ ‎7．如图，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为（　　）‎ A．40° B．45° C．50° D．55°‎ ‎8．如图，抛物线y=x2﹣2x﹣3与x轴交于点A、D，与y轴交于点C，四边形ABCD是平行四边形，则点B的坐标是（　　）‎ A．（﹣4，﹣3） B．（﹣3，﹣3） C．（﹣3，﹣4） D．（﹣4，﹣4）‎ ‎　‎ 二、填空题：每小题3分，共18分．‎ ‎9．﹣5的相反数是　　　　　　．‎ ‎10．我市2015年参加2016届中考的考生人数约为43400人，将43400用科学记数法表示为　　　　　　．‎ ‎11．如图，在△ABC中，已知DE∥BC，，则△ADE与△ABC的面积比为　　　　　　．‎ ‎12．如图，AD是△ABC的中线，G是AD上的一点，且AG=2GD，连接BG，若S△ABC=6，则图中阴影部分面积是　　　　　　．‎ ‎13．如果将抛物线y=x2+2x﹣1沿y轴向上平移，使它经过点A（1，5），那么所得新抛物线的解析式是　　　　　　．‎ ‎14．如图，△ABC是等边三角形，AC=9，以点A为圆心，AB长为半径画，若∠1=∠2，则的长为　　　　　　（结果保留π）．‎ ‎　‎ 三、解答题：本大题共10小题，共78分．‎ ‎15．计算：．‎ ‎16．电子商务的快速发展逐步改变了人们的生活方式，网购已悄然进入千家万户．李阿姨在淘宝网上花220元买了1个茶壶和10个茶杯，已知茶壶的单价比茶杯的单价的4倍还多10元．请问茶壶和茶杯的单价分别是多少元？‎ ‎17．已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根，求k的取值范围．‎ ‎18．在一个不透明的袋子里装有3个乒乓球，球上分别标有数字1，2，3，这些乒乓球除所标数字不同外其余均相同．先从袋子里随机摸出1个乒乓球，记下数字后放回，再从袋子里随机摸出1个乒乓球记下数字．请用画树状图（或列表）的方法，求两次摸出的乒乓球数字之和是奇数的概率．‎ ‎19．如图，在△ABC中，AB=AC，∠A=40°，BD是∠ABC的平分线，求∠BDC的度数．‎ ‎20．如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE⊥PD，交PD的延长线于点C，连接AD并延长，交BE于点E，且BE=6cm，求AB的长．‎ ‎21．如图是某种货车自动卸货时的示意图，AC是水平汽车底盘，OB是液压举升杠杆，货车卸货时车厢AB与底盘AC的夹角为30°，举升杠杆OB与底盘AC的夹角为75°，已知O与A的距离为4米，试求货车卸货时举升杠杆OB的长（，精确到0.01米）．‎ ‎22．感知：如图1，已知正方形ABCD，以AD、CD为一边向外作等边△ADE和等边△CDF，连接BE、EF、FB，易证△BEF是等边三角形（不用证明）；‎ 探究：将感知条件中的正方形ABCD改为矩形ABCD，如图2，其他条件不变，那么△BEF是等边三角形吗？说明理由；‎ 应用：将感知条件中的正方形ABCD改为▱ABCD，如图3，其他条件不变，则∠BEF=　　　　　　度．‎ ‎23．如图1，抛物线y1=﹣x2+a与x轴交于A、D两点，与y轴交于点B，点C（2，﹣3）在抛物线y2的图象上．‎ ‎（1）求抛物线y1的函数表达式及点B的坐标；‎ ‎（2）如图2，将抛物线y1沿x轴向右平移后得抛物线y2，且抛物线y2的图象过点C，抛物线y2与x轴交于F、G两点，顶点为E．‎ ‎①请直接写出抛物线y2的函数表达式及点E的坐标；‎ ‎②在A、B、C、D、E、F、G中，连接任意三点，能构成等腰直角三角形的共有　　　　　　个，分别是　　　　　　．‎ ‎24．如图，在菱形ABCD中，AB=6，∠ABC=60°，动点E、F同时从点B出发，其中点E从点B向点A以每秒1个单位的速度运动，点F从点B出发沿B﹣C﹣A的路线向终点以每秒2个单位的速度运动，以EF为边向上（或向右）作等边三角形EFG．AH是△ABC中BC边上的高，两点运动时间为t秒，△EFG和△AHC有重合部分时，重合部分图形的周长为L．‎ ‎（1）用含t的代数式表示线段CF的长；‎ ‎（2）求点G落在AC上时t的值；‎ ‎（3）求L关于t的函数关系式．‎ ‎　‎ ‎2016年吉林省长春市名校调研中考数学二模试卷 参考答案与试题解析 ‎　‎ 一、选择题：每小题3分，共24分．‎ ‎1．在实数﹣2，0，2，3中，最小的实数是（　　）‎ A．﹣2 B．0 C．2 D．3‎ ‎【考点】实数大小比较．‎ ‎【分析】根据正数大于0，0大于负数，可得答案．‎ ‎【解答】解：﹣2＜0＜2＜3，最小的实数是﹣2，‎ 故选：A．‎ ‎　‎ ‎2．下列图形既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎【考点】中心对称图形；轴对称图形．‎ ‎【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．‎ ‎【解答】解：A、不是轴对称图形，是中心对称图形，故本选项错误；‎ B、不是轴对称图形，是中心对称图形，故本选项错误；‎ C、不是轴对称图形，是中心对称图形，故本选项错误；‎ D、既是轴对称图形又是中心对称图形，故本选项正确．‎ 故选D．‎ ‎　‎ ‎3．如图，a∥b，将三角尺的直角顶点放在直线a上，若∠1=50°，则∠2的度数为（　　）‎ A．30° B．40° C．50° D．60°‎ ‎【考点】平行线的性质．‎ ‎【分析】先求出∠3的度数，根据平行线的性质得出∠2=∠3，代入求出即可．‎ ‎【解答】解：‎ ‎∵∠1=50°，‎ ‎∴∠3=90°﹣50≤=40°，‎ ‎∵直线a∥直线b，‎ ‎∴∠2=∠3=40°，‎ 故选B．‎ ‎　‎ ‎4．若一个正n边形的每个内角为156°，则这个正n边形的边数是（　　）‎ A．13 B．14 C．15 D．16‎ ‎【考点】多边形内角与外角．‎ ‎【分析】由一个正多边形的每个内角都为156°，可求得其外角的度数，继而可求得此多边形的边数，则可求得答案．‎ ‎【解答】解：∵一个正多边形的每个内角都为156°，‎ ‎∴这个正多边形的每个外角都为：180°﹣156°=24°，‎ ‎∴这个多边形的边数为：360°÷24°=15，‎ 故选：C．‎ ‎　‎ ‎5．已知关于x的方程2x+a﹣9=0的解是x=2，则a的值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【考点】一元一次方程的解．‎ ‎【分析】根据方程的解的定义，把x=2代入方程，解关于a的一元一次方程即可．‎ ‎【解答】解；∵方程2x+a﹣9=0的解是x=2，‎ ‎∴2×2+a﹣9=0，‎ 解得a=5．‎ 故选：D．‎ ‎　‎ ‎6．不等式组的解在数轴上表示为（　　）‎ A． B． C． D．‎ ‎【考点】在数轴上表示不等式的解集；解一元一次不等式组．‎ ‎【分析】先解每一个不等式，再根据结果判断数轴表示的正确方法．‎ ‎【解答】解：由不等式①，得3x＞5﹣2，解得x＞1，‎ 由不等式②，得﹣2x≥1﹣5，解得x≤2，‎ ‎∴数轴表示的正确方法为C．‎ 故选：C．‎ ‎　‎ ‎7．如图，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为（　　）‎ A．40° B．45° C．50° D．55°‎ ‎【考点】圆周角定理；平行线的性质．‎ ‎【分析】连接OC，由AO∥DC，得出∠ODC=∠AOD=70°，再由OD=OC，得出∠ODC=∠OCD=70°，求得∠COD=40°，进一步得出∠AOC，进一步利用圆周角定理得出∠B的度数即可．‎ ‎【解答】解：如图，‎ 连接OC，‎ ‎∵AO∥DC，‎ ‎∴∠ODC=∠AOD=70°，‎ ‎∵OD=OC，‎ ‎∴∠ODC=∠OCD=70°，‎ ‎∴∠COD=40°，‎ ‎∴∠AOC=110°，‎ ‎∴∠B=∠AOC=55°．‎ 故选：D．‎ ‎　‎ ‎8．如图，抛物线y=x2﹣2x﹣3与x轴交于点A、D，与y轴交于点C，四边形ABCD是平行四边形，则点B的坐标是（　　）‎ A．（﹣4，﹣3） B．（﹣3，﹣3） C．（﹣3，﹣4） D．（﹣4，﹣4）‎ ‎【考点】抛物线与x轴的交点；平行四边形的性质．‎ ‎【分析】首先利用抛物线与坐标轴的交点坐标求出A、D、C的坐标，再利用平行四边形的性质得出B点坐标．‎ ‎【解答】解：令y=0，可得x=3或x=﹣1，‎ ‎∴A点坐标为（﹣1，0）；D点坐标为（3，0）；‎ 令x=0，则y=﹣3，‎ ‎∴C点坐标为（0，﹣3），‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD=BC，AD∥BC，‎ ‎∵AD=BC=4，‎ ‎∴B点的坐标为（﹣4，﹣3），‎ 故选A．‎ ‎　‎ 二、填空题：每小题3分，共18分．‎ ‎9．﹣5的相反数是　5　．‎ ‎【考点】相反数．‎ ‎【分析】根据相反数的定义直接求得结果．‎ ‎【解答】解：﹣5的相反数是5．‎ 故答案为：5．‎ ‎　‎ ‎10．我市2015年参加2016届中考的考生人数约为43400人，将43400用科学记数法表示为　4.34×104　．‎ ‎【考点】科学记数法—表示较大的数．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于5100000有7位，所以可以确定n=7﹣1=6．‎ ‎【解答】解：43400=4.34×104．‎ 故答案为4.34×104．‎ ‎　‎ ‎11．如图，在△ABC中，已知DE∥BC，，则△ADE与△ABC的面积比为　4：25　．‎ ‎【考点】相似三角形的判定与性质．‎ ‎【分析】根据题意可得△ADE∽△ABC，然后根据面积比为相似比的平方求解．‎ ‎【解答】解：在△ABC中，‎ ‎∵DE∥BC，‎ ‎∴△ADE∽△ABC，‎ ‎∵，‎ ‎∴S△ADE：S△ABC=4：25．‎ 故答案为：4：25．‎ ‎　‎ ‎12．如图，AD是△ABC的中线，G是AD上的一点，且AG=2GD，连接BG，若S△ABC=6，则图中阴影部分面积是　2　．‎ ‎【考点】三角形的面积．‎ ‎【分析】根据三角形的中线的性质进行解答即可．‎ ‎【解答】解：∵S△ABC=6，‎ ‎∴S△ABD=3，‎ ‎∵AG=2GD，‎ ‎∴S△ABG=2，‎ 故答案为：2‎ ‎　‎ ‎13．如果将抛物线y=x2+2x﹣1沿y轴向上平移，使它经过点A（1，5），那么所得新抛物线的解析式是　y=x2+2x+2　．‎ ‎【考点】二次函数图象与几何变换．‎ ‎【分析】先把解析式配成顶点式得到抛物线的顶点坐标为（﹣1，﹣2），再利用点平移的坐标规律，把点（﹣1，﹣2）向上平移m个单位所得对应点的坐标为（﹣1，﹣2+m），则根据顶点式写出平移的抛物线解析式为y=（x+1）2﹣2+m，然后把A点坐标代入求出m的值即可得到平移后得到的抛物线的解析式．‎ ‎【解答】解：因为y=y=x2+2x﹣1=（x+1）2﹣2，所以抛物线的顶点坐标为（﹣1，﹣2），点（﹣1，﹣2）向上平移m个单位所得对应点的坐标为（﹣1，﹣2+m），所以平移的抛物线解析式为y=（x+1）2﹣2+m，把A（1，5）代入得 ‎4﹣2+m=5，解得m=3，所以平移后的抛物线解析式为y=（x+1）2+1，即y=x2+2x+2．‎ 故答案为y=x2+2x+2．‎ ‎　‎ ‎14．如图，△ABC是等边三角形，AC=9，以点A为圆心，AB长为半径画，若∠1=∠2，则的长为　3π　（结果保留π）．‎ ‎【考点】弧长的计算．‎ ‎【分析】先由等边三角形的性质得出AB=AC=9，∠CAB=60°．再由∠1=∠2得到∠CAB=∠DAE=60°，然后根据弧长公式解答即可．‎ ‎【解答】解：∵△ABC是等边三角形，AC=9，‎ ‎∴AB=AC=9，∠CAB=60°．‎ ‎∵∠1=∠2，‎ ‎∴∠1+∠BAD=∠2+∠BAD，‎ ‎∴∠CAB=∠DAE=60°，‎ ‎∴弧DE的长为=3π，‎ 故答案为：3π．‎ ‎　‎ 三、解答题：本大题共10小题，共78分．‎ ‎15．计算：．‎ ‎【考点】二次根式的混合运算．‎ ‎【分析】先进行乘法运算，然后把化简后合并即可．‎ ‎【解答】解：原式=2+2+5‎ ‎=4+5．‎ ‎　‎ ‎16．电子商务的快速发展逐步改变了人们的生活方式，网购已悄然进入千家万户．李阿姨在淘宝网上花220元买了1个茶壶和10个茶杯，已知茶壶的单价比茶杯的单价的4倍还多10元．请问茶壶和茶杯的单价分别是多少元？‎ ‎【考点】二元一次方程组的应用．‎ ‎【分析】设茶壶的单价为x元，茶杯的单价为y元，根据题意可得，1个茶壶和10个茶杯共花去220元，茶壶的单价比茶杯的单价的4倍还多10元，据此列方程组求解．‎ ‎【解答】解：设茶壶的单价为x元，茶杯的单价为y元，‎ 由题意得，，‎ 解得：．‎ 答：茶壶的单价为70元，茶杯的单价为15元．‎ ‎　‎ ‎17．已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根，求k的取值范围．‎ ‎【考点】根的判别式；解一元一次不等式．‎ ‎【分析】由方程有两个不相等的实数根即可得出△＞0，代入数据即可得出关于k的一元一次不等式，解不等式即可得出结论．‎ ‎【解答】解：∵关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根，‎ ‎∴△=（﹣6）2﹣4（k+3）=24﹣4k＞0，‎ 解得：k＜6．‎ ‎　‎ ‎18．在一个不透明的袋子里装有3个乒乓球，球上分别标有数字1，2，3，这些乒乓球除所标数字不同外其余均相同．先从袋子里随机摸出1个乒乓球，记下数字后放回，再从袋子里随机摸出1个乒乓球记下数字．请用画树状图（或列表）的方法，求两次摸出的乒乓球数字之和是奇数的概率．‎ ‎【考点】列表法与树状图法．‎ ‎【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的乒乓球标号数字之和是奇数的情况，再利用概率公式即可求得答案即可．‎ ‎【解答】解：画树状图得：‎ ‎∵共有9种等可能的结果，两次摸出的乒乓球标号数字之和是奇数有4种情况，‎ ‎∴两次摸出的乒乓球标号数字之和是奇数概率=．‎ ‎　‎ ‎19．如图，在△ABC中，AB=AC，∠A=40°，BD是∠ABC的平分线，求∠BDC的度数．‎ ‎【考点】等腰三角形的性质；三角形内角和定理．‎ ‎【分析】首先由AB=AC，利用等边对等角和∠A的度数求出∠ABC和∠C的度数，然后由BD是∠ABC的平分线，利用角平分线的定义求出∠DBC的度数，再根据三角形的内角和定理即可求出∠BDC的度数．‎ ‎【解答】解：∵AB=AC，∠A=40°，‎ ‎∴∠ABC=∠C==70°，‎ ‎∵BD是∠ABC的平分线，‎ ‎∴∠DBC=∠ABC=35°，‎ ‎∴∠BDC=180°﹣∠DBC﹣∠C=75°．‎ ‎　‎ ‎20．如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE⊥PD，交PD的延长线于点C，连接AD并延长，交BE于点E，且BE=6cm，求AB的长．‎ ‎【考点】切线的性质．‎ ‎【分析】连接OD，利用切线的性质解答即可．‎ ‎【解答】解：连接OD，‎ ‎∵PD切⊙O于点D，‎ ‎∴OD⊥PD，‎ ‎∵BE⊥PC，‎ ‎∴OD∥BE，‎ ‎∴∠ADO=∠E，‎ ‎∵OA=OD，‎ ‎∴∠OAD=∠ADO，‎ ‎∴∠OAD=∠E，‎ ‎∴AB=BE=6（cm）．‎ ‎　‎ ‎21．如图是某种货车自动卸货时的示意图，AC是水平汽车底盘，OB是液压举升杠杆，货车卸货时车厢AB与底盘AC的夹角为30°，举升杠杆OB与底盘AC的夹角为75°，已知O与A的距离为4米，试求货车卸货时举升杠杆OB的长（，精确到0.01米）．‎ ‎【考点】解直角三角形的应用．‎ ‎【分析】过点O作OE⊥AB于E，先在Rt△AEO中求出EO，再在Rt△EBO中求出OB即可解决问题．‎ ‎【解答】解：过点O作OE⊥AB于E，‎ ‎∵∠BOC=75°，∠A=30°，‎ ‎∴∠ABO=45°，‎ 在Rt△AEO中，OE=OA=2，‎ 在Rt△BEO中，∠ABO=∠BOE，‎ ‎∴BE=EO，‎ ‎∴OB=OE，‎ ‎∴OB=2×≈2.83（米），‎ 答：货车卸货时举升杠杆OB的长约为2.83米．‎ ‎　‎ ‎22．感知：如图1，已知正方形ABCD，以AD、CD为一边向外作等边△ADE和等边△CDF，连接BE、EF、FB，易证△BEF是等边三角形（不用证明）；‎ 探究：将感知条件中的正方形ABCD改为矩形ABCD，如图2，其他条件不变，那么△BEF是等边三角形吗？说明理由；‎ 应用：将感知条件中的正方形ABCD改为▱ABCD，如图3，其他条件不变，则∠BEF=　60　度．‎ ‎【考点】四边形综合题．‎ ‎【分析】感知：利用SAS即可证明两三角形的全等，再证明△ABE≌△DFE，可得△BEF是等边三角形；‎ 探究：求出∠BAE，∠EDF，∠FCB的度数，继而证明△ABE≌△CFB≌△DFE，即可得出结论；‎ 应用：证明方法与探究完全相同，证出结论即可．‎ ‎【解答】解：感知：证明：∠BAE=90°+60°=150°，∠FCB=90°+60°=150°，‎ 在△ABE和△CFB中，‎ ‎，‎ ‎∴△ABE≌△CFB（SAS）．‎ ‎∠FDE=360°﹣60°﹣60°﹣90°=150°，‎ 在△ABE和△DFE中，‎ ‎，‎ ‎∴△ABE≌△DFE（SAS），‎ ‎∴BE=FE，‎ 又∵△ABE≌△CFB，‎ ‎∴BE=FB=FE，‎ ‎∴△BFE是等边三角形；‎ 探究：△BEF是等边三角形，理由如下：‎ ‎∠BAE=90°+60°=150°，∠FCB=90°+60°=150°，∠FDE=360°﹣60°﹣60°﹣90°=150°，‎ 在△ABE和△CFB中，‎ ‎，‎ ‎∴△ABE≌△CFB（SAS），‎ 在△ABE和△DFE中，‎ ‎，‎ ‎∴△ABE≌△DFE（SAS），‎ ‎∴△ABE≌△CFB≌△DFE，‎ ‎∴BE=EF=FB，‎ ‎∴△BEF是等边三角形；‎ 应用：∵四边形ABCD是平行四边形，‎ ‎∴AB=CD，AD=BC，∠BAD=∠BCD，‎ ‎∵△ADE和△CDF是等边三角形，‎ ‎∴AE=AD=BC，AB=DC=CF，‎ 在△ABE与△FCB中，，‎ ‎∴△ABE≌△FCB，‎ ‎∴BE=BF，‎ ‎∵∠BAE=∠BAD+∠EAD=∠BAD+60°，‎ ‎∠EDF=360°﹣∠ADC﹣∠ADE﹣∠CDF=∠BAD+60°，‎ ‎∴∠EDF=∠BAE，‎ 在△ABE与△EDF中，，‎ ‎∴△ABE≌△EDF，‎ ‎∴BE=EF，∠AEB=∠DEF，‎ ‎∴∠BEF=60．‎ 故答案为：60°．‎ ‎　‎ ‎23．如图1，抛物线y1=﹣x2+a与x轴交于A、D两点，与y轴交于点B，点C（2，﹣3）在抛物线y2的图象上．‎ ‎（1）求抛物线y1的函数表达式及点B的坐标；‎ ‎（2）如图2，将抛物线y1沿x轴向右平移后得抛物线y2，且抛物线y2的图象过点C，抛物线y2与x轴交于F、G两点，顶点为E．‎ ‎①请直接写出抛物线y2的函数表达式及点E的坐标；‎ ‎②在A、B、C、D、E、F、G中，连接任意三点，能构成等腰直角三角形的共有　5　个，分别是　△ABD、△EFG、△ACE、△BCF、△DCG　．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）根据抛物线y1=﹣x2+a与x轴交于A、D两点，与y轴交于点B，点C（2，﹣3）在抛物线y1的图象上，可以求得抛物线y1的函数表达式及点B的坐标；‎ ‎（2）①根据抛物线y1沿x轴向右平移后得抛物线y2，且抛物线y2的图象过点C，顶点为E，可以得到抛物线y2的函数表达式及点E的坐标；‎ ‎②先求出点A、B、C、D、E、F、G各点的坐标，然后即可得到能够成等腰直角三角形的个数，通过计算可以说明哪几个三角形是等腰直角三角形．‎ ‎【解答】解：（1）把点C（2，﹣3）代入y1=﹣x2+a，得 ‎﹣3=﹣22+a，‎ 解得，a=1，‎ 即y1=﹣x2+1，‎ 当x=0时，y1=1，‎ 即点B的坐标为（0，1）；‎ ‎（2）①抛物线y2的函数表达式为：，点E的坐标为（4，1）；‎ 理由：设，‎ ‎∵点C（2，﹣3）在抛物线y2的图象上，‎ ‎∴﹣3=﹣（2+b）2+1，‎ 解得，b=﹣4，‎ 即，‎ ‎∴点E的坐标为（4，1）；‎ ‎（3）当y1=0代入y1=﹣x2+1，得x=﹣1或x=1，将x=0代入y1=﹣x2+1，得y1=1，‎ ‎∴点D为（﹣1，0），点A为（1，0），点B为（0，1），‎ 将y2=0代入，得x=3或x=5，将x=4代入，得y2=1，‎ ‎∴点F（3，0），G为（5，0），E为（4，1），‎ ‎∴BD=，AB=，AD=2，‎ ‎∵，‎ ‎∴△ABD是等腰直角三角形；‎ ‎∴EF=，EG=，FG=2，‎ ‎，∵，‎ ‎∴△EFG是等腰直角三角形；‎ ‎∵A为（1，0），C为（2，﹣3），E为（4，1），‎ ‎∴AC=，AE=，CE=，‎ ‎∵，‎ ‎∴△ACE是等腰直角三角形；‎ ‎∵点B为（0，1），C为（2，﹣3），点F（3，0），‎ ‎∴BC=，BF=，CF=，‎ ‎∵，‎ ‎∴△BCF是等腰直角三角形；‎ ‎∵点D为（﹣1，0），C为（2，﹣3），G为（5，0），‎ ‎∴DC=，DG=，CG=，‎ ‎∵，‎ ‎∴△CDG是等腰直角三角形；‎ 故答案为：5，△ABD、△EFG、△BFC、△ACE、△CDG．‎ ‎　‎ ‎24．如图，在菱形ABCD中，AB=6，∠ABC=60°，动点E、F同时从点B出发，其中点E从点B向点A以每秒1个单位的速度运动，点F从点B出发沿B﹣C﹣A的路线向终点以每秒2个单位的速度运动，以EF为边向上（或向右）作等边三角形EFG．AH是△ABC中BC边上的高，两点运动时间为t秒，△EFG和△AHC有重合部分时，重合部分图形的周长为L．‎ ‎（1）用含t的代数式表示线段CF的长；‎ ‎（2）求点G落在AC上时t的值；‎ ‎（3）求L关于t的函数关系式．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）由菱形的性质得出BC=AB=6得出CF=BC﹣BF=6﹣2t即可；‎ ‎（2）由菱形的性质和已知条件得出△ABC是等边三角形，得出∠ACB=60°，由等边三角形的性质和三角函数得出∠GEF=60°，GF=EF=BF•sin60°=t，证出∠GFC=90°，由三角函数求出CF==t，由BF+CF=BC得出方程，解方程即可；‎ ‎（3）分三种情况：①当＜t≤2时，根据梯形的周长公式即可得出结果；②当2＜t≤3时，由①的结果容易得出结论；③当3＜t＜6时，由①的结果容易得出结论．‎ ‎【解答】‎ 解：（1）根据题意得：BF=2t，‎ ‎∵四边形ABCD是菱形，‎ ‎∴BC=AB=6，‎ ‎∴CF=BC﹣BF=6﹣2t；‎ 故答案为：6﹣2t；‎ ‎（2）点G落在线段AC上时，如图1所示：‎ ‎∵四边形ABCD是菱形，‎ ‎∴AB=BC，‎ ‎∵∠ABC=60°，‎ ‎∴△ABC是等边三角形，‎ ‎∴∠ACB=60°，‎ ‎∵△EFG是等边三角形，‎ ‎∴∠GFE=60°，GF=EF=BF•sin60°=t，‎ ‎∵EF⊥AB，‎ ‎∴∠BFE=90°﹣60°=30°，‎ ‎∴∠GFB=90°，‎ ‎∴∠GFC=90°，‎ ‎∴CF===t，‎ ‎∵BF+CF=BC，‎ ‎∴2t+t=6，‎ 解得：t=2；‎ ‎（3）当＜t≤2时，如图2，L=2t+（2t﹣3）=﹣2，‎ 当2＜t≤3时，如图3所示：L=t+（6﹣t）×+[6﹣（6﹣t）﹣2（6﹣2t）]+（6﹣2t）=+7﹣9，‎ 当3＜t＜6时，如图4，L=（6﹣t）+×（6﹣t）+（6﹣t）×=﹣+7+9．‎