2019届中考数学一轮复习 第20课时 中心对称图形导学案（无答案）

2019届中考数学一轮复习 第20课时 中心对称图形导学案（无答案）

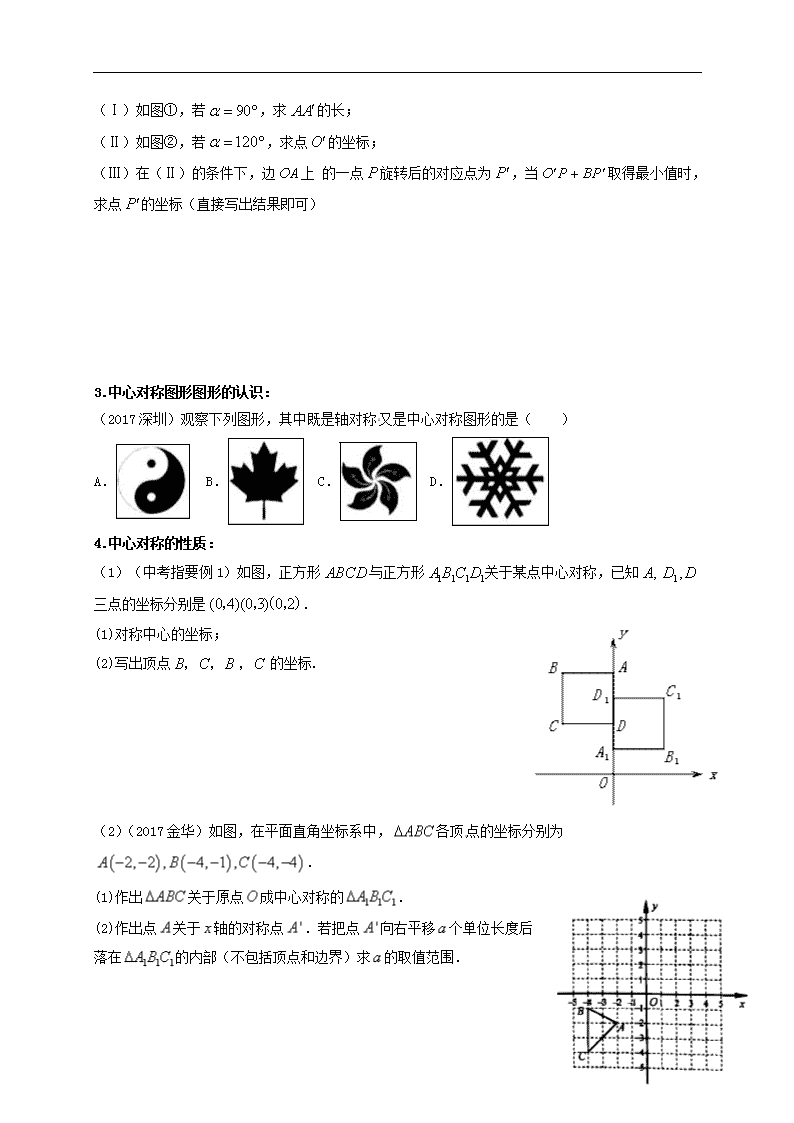
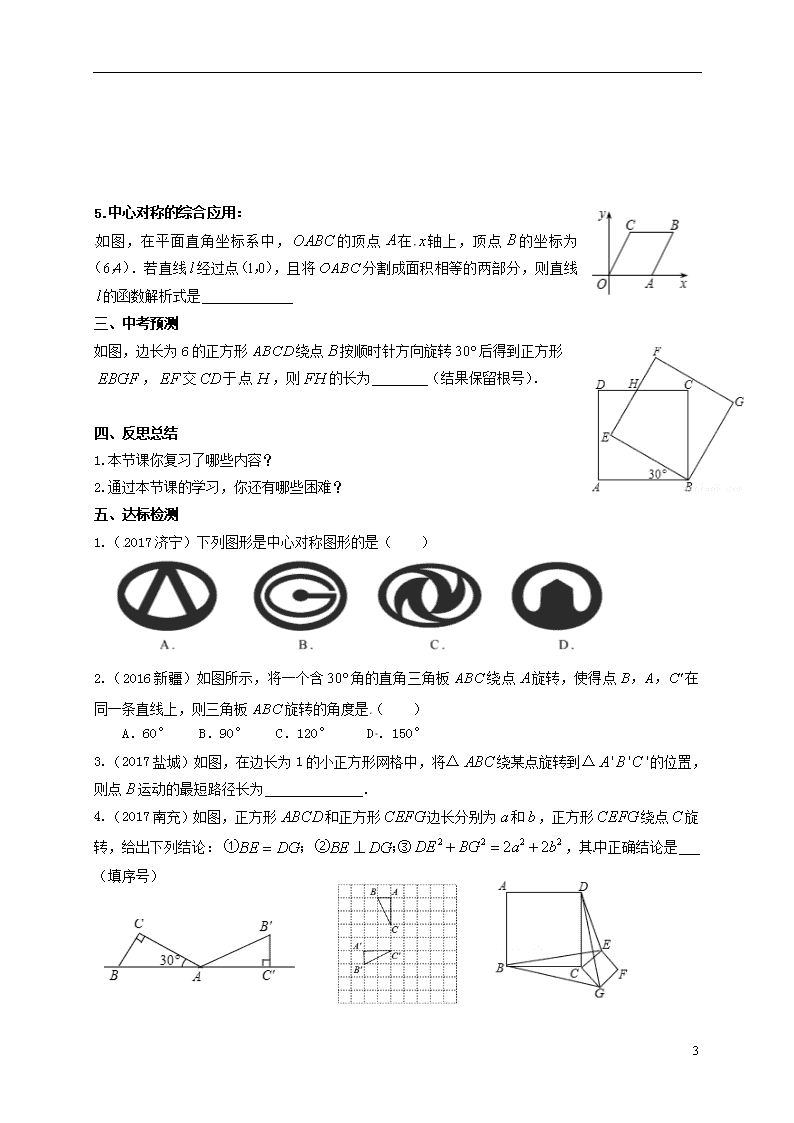
第20课时 中心对称图形 班级： 姓名： ‎ 学习目标：1.掌握图形的旋转、中心对称与中心对称图形的性质；‎ ‎2.利用旋转、中心对称的知识解决相关问题 重难点：2.利用旋转、中心对称的知识解决相关问题 ‎ 学习过程 一．知识梳理 ‎1.旋转的特征 ‎（1）经过旋转，图形中每一个点都绕着旋转中心旋转了相同的 。‎ ‎（2）对应线段、对应角都 ，对应点到旋转中心的距离 。‎ ‎2.中心对称与中心对称图形 ‎（1）一个图形绕着某点旋转 °后与自身重合，这种图形叫做 。‎ ‎（2）一个图形绕着某点旋转 °后另一个图形重合，这两个图形成 。‎ ‎（3）在成中心对称的两个图形中，连接对应点的线段都经过 ，并且被它 。‎ 二、典型例题 ‎1.旋转的性质：‎ ‎（1）（2017宜宾）如图，将△绕点按逆时针方向旋转后得到△，若，则的度数是　 　．‎ ‎（2）（2017泰安）如图，在正方形网格中，线段是线段绕某点逆时针旋转角得到的，点与对应，则角的大小为（　　）‎ ‎ A．30° B．60° C．90° D．120°‎ ‎2.旋转的综合应用：‎ ‎（中考指要例2）（2016天津）在平面直角坐标系中，为原点，点，点，把△绕点逆时针旋转，得△，点旋转后的对应点为，记旋转角为．‎ 4‎ ‎（Ⅰ）如图①，若，求的长；‎ ‎（Ⅱ）如图②，若，求点的坐标；‎ ‎（Ⅲ）在（Ⅱ）的条件下，边上 的一点旋转后的对应点为，当取得最小值时，求点的坐标（直接写出结果即可）‎ ‎3.中心对称图形图形的认识：‎ ‎（2017深圳）观察下列图形，其中既是轴对称又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎4.中心对称的性质：‎ ‎（1）（中考指要例1）如图，正方形与正方形关于某点中心对称，已知三点的坐标分别是.‎ ‎(1)对称中心的坐标；‎ ‎(2)写出顶点的坐标.‎ ‎ ‎ ‎（2）（2017金华）如图，在平面直角坐标系中，各顶点的坐标分别为．‎ ‎(1)作出关于原点成中心对称的．‎ ‎(2)作出点关于轴的对称点．若把点向右平移个单位长度后落在的内部（不包括顶点和边界）求的取值范围．‎ 4‎ ‎5.中心对称的综合应用：‎ 如图，在平面直角坐标系中，的顶点在轴上，顶点的坐标为．若直线经过点，且将分割成面积相等的两部分，则直线的函数解析式是 ‎ 三、中考预测 如图，边长为6的正方形绕点按顺时针方向旋转后得到正方形，交于点，则的长为    （结果保留根号）． ‎ 四、反思总结 ‎1.本节课你复习了哪些内容？‎ ‎2.通过本节课的学习，你还有哪些困难？‎ 五、达标检测 ‎1.（2017济宁）下列图形是中心对称图形的是（　　）‎ ‎ ‎ ‎2.（2016新疆）如图所示，将一个含角的直角三角板绕点旋转，使得点在同一条直线上，则三角板旋转的角度是（　　）‎ A．60° B．90° C．120° D．150°‎ ‎3.（2017盐城）如图，在边长为1的小正方形网格中，将△绕某点旋转到△的位置，则点运动的最短路径长为 ．‎ ‎4.（2017南充）如图，正方形和正方形边长分别为和，正方形绕点旋转，给出下列结论：③，其中正确结论是 （填序号）‎ 4‎ ‎5.（中考指要例3）（2015潍坊）如图1，点是正方形两对角线的交点，分别延长到点，到点，使，然后以为邻边作正方形，连接．‎ ‎（1）求证：；‎ ‎（2）正方形固定，将正方形绕点逆时针旋转角（）得到正方形，如图2．‎ ‎①在旋转过程中，当是直角时，求的度数；‎ ‎②若正方形的边长为1，在旋转过程中，求长的最大值和此时的度数，直接写出结果不必说明理由．（可在下页书写）‎ ‎6.（中考指要第8题）（2013潍坊）如图1所示，将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起，构成一个大的长方形.现将小长方形绕点顺时针旋转至,旋转角为.‎ ‎（1）当点恰好落在边上时，求旋转角的值；‎ ‎（2）如图2，为的中点，且0°＜＜90°，求证：；‎ ‎（3）小长方形绕点顺时针旋转一周的过程中，与能否全等？若能，直接写出旋转角的值；若不能，说明理由.‎ 4‎