广州各区数学中考一模压轴题汇总无答案
一、 选择填空
(一)从化区
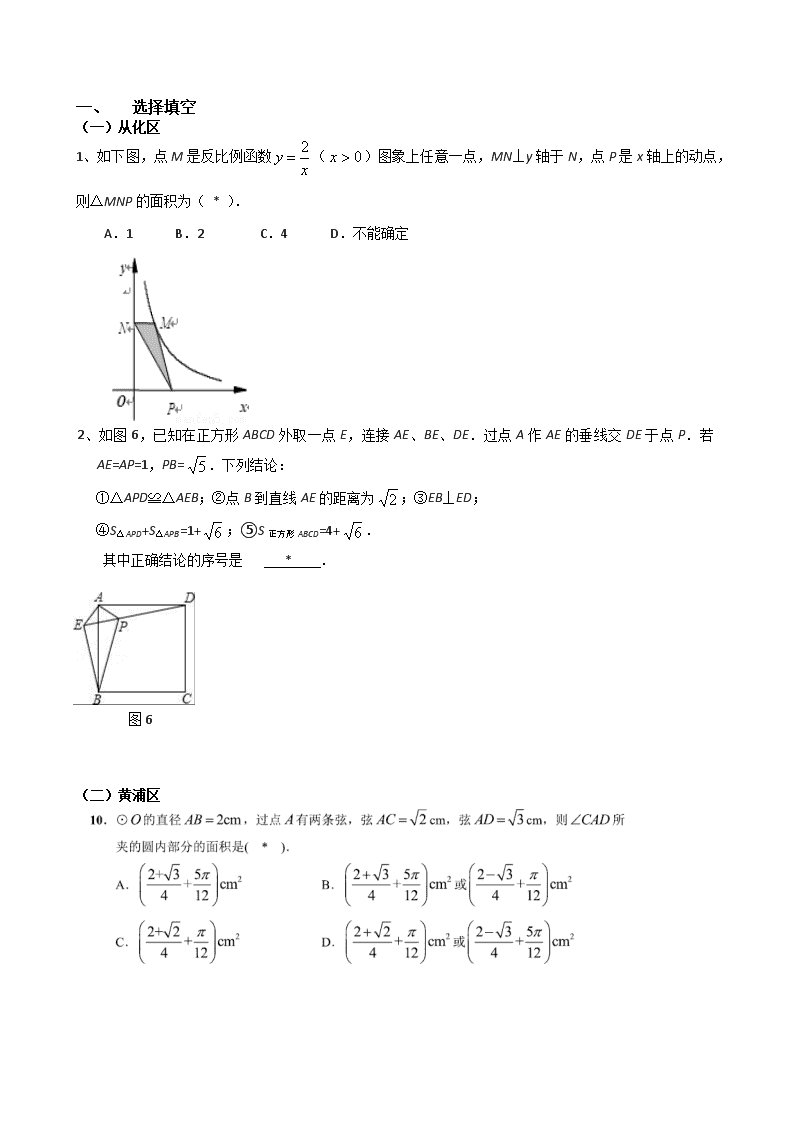
1、如下图,点M是反比例函数()图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( * ).
A.1 B.2 C.4 D.不能确定
2、如图6,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:
①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;
④S△APD+S△APB=1+;⑤S正方形ABCD=4+.
其中正确结论的序号是 * .
图6
(二)黄浦区
(三)铁一中学
1、定义为函数的特征函数,下面给出特征数为的函数的一些结论:①当时,函数图像的顶点坐标是;②当时,函数图像截轴所得的线段长度大于;③当时,函数在时,随的增大而减小;④不论取任何值,函数图像经过两个定点。其中正确的结论有( )
A.个
B.个
C.个
D. 个
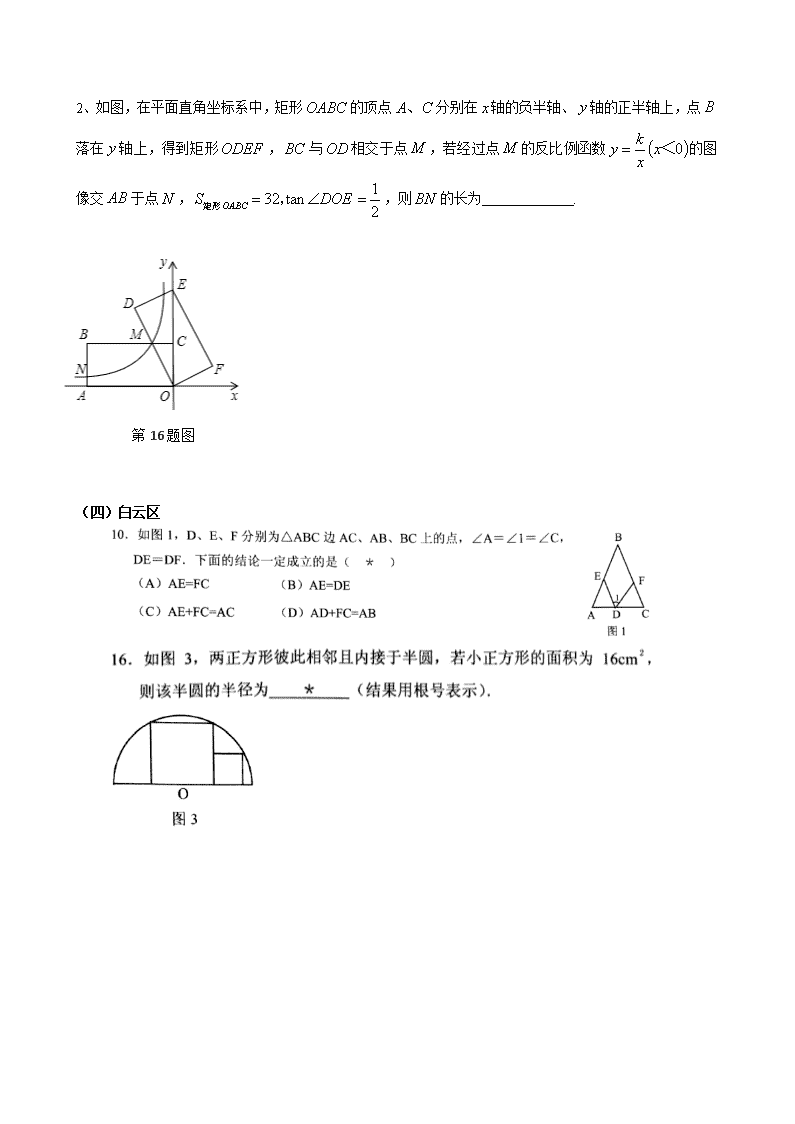
2、如图,在平面直角坐标系中,矩形的顶点分别在轴的负半轴、轴的正半轴上,点落在轴上,得到矩形,与相交于点,若经过点的反比例函数的图像交于点,,则的长为 .
第16题图
(四)白云区
(五) 八一中学
1、如图为某几何体的三视图,这个几何体的名称为 ,如果一只蚂蚁要从这个几何体中的点出发,沿表面爬到的中点,请求出这个路线的最短路程为 厘米。
第16题图
(六) 番禺区
1、抛物线与x轴交于A、B两点,点P在函数的图像上,若△PAB为直角三角形,则满足条件的点P的个数为( )
【A】2个;
【B】3个;
【C】4个;
【D】6个.
2、直线y=x-2与x轴、y轴分别交于点B、C,与反比例函数(k>0)的图象在第一象限交于点A,连接OA,若S△AOB:S△BOC=1:2,则k的值为( )
(七)海珠区
10、正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE’。点F是DE的中点,连接AF、BF、E’F’。若AE=.下列结论:①AD垂直平分EE’;②tan∠ADE=;③;④。其中结论正确的是( )
16、设关于x的方程有两个不相等的实数根,且,那么k的取值范围是
(八)花都区
10. 如图,在矩形中,点在上,点在上,把这个矩形沿折叠后,使点恰好落在边上的点处,若矩形面积为且,,则折痕的长为( D )
A. B. C. D.
16.如图,,点在边上,,过点作交于点,以为边在外侧作等边三角形,再过点作,分别交,于点、,再以为边在的外侧作等边三角形……按此规律进行下去,则第个等边三角形的周长为 ,第个等边三角形的周长为 .(用含的代数式表示)
(九)华工附中
10.已知二次函数的图象如图所示,并且关于的一元二次方程有两个不相等的实数根,下列结论:
①;②;③;④.
其中,正确的个数有( ).
A. B. C. D.
16.已知二次函数,当时,的值随值的增大而增大,则实数的取值范围是__________.
(十)广雅
10.如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至的位置,此时点的横坐标为3,则点的坐标为( )
A.(4,) B.(3,) C.(4,) D.(3,)
16.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF.分析下列四个结
论:①△AEP∽△CAB;②CF=2AF;③DF=DC;④.其中正确的结论是_____.
(十一)四中
10.如图,PA、PB切○O于A、B两点,CD切○O于点E交PA,PB于C,D. 若○O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A. 125 B.51213
C. 3513 D. 2313
16.如图,已知:点A是双曲线y=2x在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限,随着点A的运动,点C得位置也不断变化,但点C始终在双曲线y=kx(k>0)上运动,则k的值是 。
(十二)西关外国语
10.如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0∘<θ<90∘),PM、PN分别交AB、BC于E. F两点,连接EF交OB于点G,则下列结论中正确的是( ).
(1)EF=OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=;(5)OG⋅BD=AE 2+CF 2.
A、(1)(2)(3)(5) B.(1)(3)(4)(5)
C.(2)(3)(4)(5) D.(1)(2)(3)(4)
15.边长为1的正方形OA1B1C1的顶点A1在X轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为___.
16、 已知m,n是关于x的方程(k+1)x2−x+1=0的两个实数根,且满足k+1=(m+1)(n+1),则实数k的值是___.
(十三)南沙区
10、如图,□ABCD 的对角线 AC 与 BD 相交于点 O , OE ^ BC ,垂足为 E ,
AB =, AC = 4 , BD = 6 ,则 OE 的长为 ( ※ )
A. B. C. D.
16.如下图,已知等边 ΔABC 的边长为 6,在 AC , BC 边上各取一点 E , F ,使
AE = CF ,连接 AF 、 BE 相交于点 P ,当点 E 从点 A 运动到点 C 时,点 P 经过 点的路径长为 ※ 。
(十四)十六中
10、中,,点在上,且,点是的中点,过点分别作于点,于点,则等于( )
A.
B.
C.
D.
16已知点与点是一平行四边形的四个顶点,则长的最小值为 。
(十五)天河区
10、 如图,菱形中,,点分别为边上的点,且,连接交于点,则下列结论正确的个数是( )
①;②;③;④;
A.个
B.个
C.个
D.个
第10题
16、如图,已知正方形边长为,点在边上,且,点分别是边的动点(均不予顶点重合),当四边形的周长取最小值时,四边形的面积是 。
第16题
(十六)二中
(十七)知用中学
9.如图2,△ABC是等边三角形,D是BC边上一点,将△ABD绕点A逆时针旋转60°得到△ACE,连接DE,则下列说法不一定正确的是( * ).
图2
A.△ADE是等边三角形 B.AB∥CE
C.∠BAD=∠DEC D.AC=CD+CE
10.已知二次函数的图象如图3所示,则反比例函数与一次函数的图象可能是( * ).
图3
A. B. C. D.
16. 如图6,E、F分别是正方形ABCD的边AD、CD上的点,且AE=DF,AF、BE相交于点P,设AB=,AE=,则下列结论:①△ABE≌△DAF;②AF⊥BE;
③;④若,连接BF,则tan∠EBF=.其中正确的结论
是 * .(填写所有正确结论的序号)
(十八)增城
10.如图 5,直线 y = x + 4 与 x 轴、 y 轴分别交于点 A 和点 B ,点 C 、 D 分别为线段 AB 、OB 的
中点,点 P 为 OA 上一动点,当 PC + PD 最小时,点 P 的坐标为( ※ )
A. (-3,0) B. (-6,0) C.(-,0) D.(-,0)
16.如图 7,在正方形 ABCD 中,边长为 2 的等边 DAEF 顶点 E 、F 分别在 BC 和CD 上,下列结论:
① CE = CF ; ② ÐAEB = 75° ; ③ BE + DF = EF ; ④ S正方形ABCD = 2 +
其中正确的序号是 ※ (把你认为正确的都填上).
`
(十九)育才中学
10.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A B C D
16.以点O为圆心,以1为半径的圆上有一动点B,点A是圆O外一点,AO=2,△ABC是以线段AB为边所作的等边三角形,连接OC,当点B在圆O上运动时,则OC的最大值为________
(二十)省实天河
9、
10、
16、
一、 压轴题
(一)从化
24.(本小题满分14分)
如图11,在平面直角坐标系中,二次函数的图象与轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,求使△QBC为直角三角形的点Q的坐标.
图11
25.(本小题满分14分)
如图12,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.
(1)若m=2时,求∠BCD、∠ACD的度数各是多少?
图12
(2)当时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由;
(3)在(1)的条件下,且,求弦CD的长.
(二)黄浦区
(三)铁一中学
1、我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形,若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1) “等边三角形”“内似线”的条数为 ;
(2) 如图,中,,点在上,且,求证:是的“内似线”;
(3) 在中,,,点分别在边上,且是的“内似线”,求的长。
2、已知抛物线经过三点,其对称轴交轴于点,一次函数的图像过点,与抛物线交于另一点(点在点的左边),与抛物线的对称轴交于点.
(1) 求该抛物线的解析式;
(2) 如图,当时,求一次函数的解析式;
(3) 如图,设,当时,求出的取值范围。
(四)白云区
(五)八一中学
1、如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值,如果是,请求出此定值,如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.
2如图,是的直径,,点为线段上一点(不与重合),作,交于点,垂足为点,作直径,过点的切线交的延长线于点,于点,连接。
(1) 求证:是的平分线;
(2) 求证:;
(3) 当时,求劣弧的长度。
(六)番禺区
1、如图本题图①,在等腰Rt△OAB中,OA=OB=3,OA⊥OB,P为线段AO上一点,以OP为半径作圆O交OB于点Q,连接BP、PQ,线段BP、AB、PQ的中点为D、M、N。
(1) 试探究△DMN是什么特殊三角形?说明理由。
(2) 将△OPQ绕点O逆时针方向旋转到图②的位置,其结论是否仍然成立?并给予证明
(3) 设OP=x(0
0),当时,函数有最大值5.
(1) 求此二次函数图象与坐标轴的交点。
(2) 将此图象x轴下方的部分沿x轴向上翻折,所得到的图象与直线y=n恒有四个交点,从左到右四个交点依次记为A、B、C、D,当以BC为直径的圆与x轴相切时,求n的值。
(3) 若点P(x0,y0)是(2)中翻折所得的抛物线弧上的一点,当关于m的一元二次方程恒有实数根时,求实数k的最大值。
(七)海珠区
24、(14分)如图,在菱形OABC中,已知点B(8,4)C(5,0)。点D为OB、AC交点,点P从原点出发向x轴正方向运动。
(1)在点P运动过程中,若∠OBP=90°,求点P的坐标
(2)在点P运动过程中,若∠PDC+∠BCP=90°,求点P的坐标
(3)点P在(2)位置时停止运动,点M从点P出发沿x轴正方向运动,连结BM。若点P关于BM的对称点P’到AB所在直线的距离为2,求此时点M的坐标。
25、 如图,在平面直角坐标系中,已知二次函数的图像经过A(-1,0),B(3,0),C(6,4)三点
(1) 求二次函数解析式和顶点D的坐标;
(2) ①E为抛物线对称轴上一点,过点E作FG//x轴,分别交抛物线于F、G两点,若,求点E的坐标;
②若抛物线对称轴上点H到直线BC的距离等于点H到x轴的距离,则求出点H的坐标;
(3) 在(2)条件下,以点I(1,)为圆心,IH的长为半径作⊙I,J为⊙I上的动点,求是否存在一个定值λ,使得的最小值是,若存在,请求出λ的值;若不存在,请说明理由。
(八)花都
24. (本小题满分14分)
已知二次函数的图象经过,,与x轴交于点.
(1) 求这个二次函数的解析式;
(2) 点直线下方抛物线上的一动点,求面积的最大值;
(3)在抛物线对称轴上是否存在点,使是直角三角形?若存在,直接写出点的坐标,若不存在,请说明理由.
25. (本小题满分14分)
已知,如图1,正方形的边长为,点、分别在边、的延长线上,且,连接.
(1)证明:;
(2)将绕点顺时针方向旋转,当旋转角满足时,设与射线交于点G,与AC交于点H,如图所示,试判断线段,,的数量关系,并说明理由.
A
B
E
C
D
F
图1
(3)若将绕点旋转一周,连接、,并延长交直线于点,连接,试说明点的运动路径并求线段的取值范围.
A
B
E
C
D
F
图2
H
A
B
C
D
E
F
图3
G
第25题图
(九)华工附中
24.如图,在平面直角坐标系中,抛物线经过点、,与轴交于点,直线交轴交于点,交抛物线于、两点,点为线段上一个动点(与、不重合),轴与抛物线交于点.
()求抛物线的解析式.
()当在什么位置时,四边形为平行四边形?求出此时点的坐标.
()是否存在点使为等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
25.问题背景
甲、乙、丙三名同学探索课本上一道题:如图,是边长为的正方形中边上任意一点,以点为中心,把顺时针旋转,画出旋转后的图形.
任务要求:
()请你在图中画出旋转后的图形
甲、乙、丙三名同学又继续探索:
在正方形中,,点为上一点,点为上一点,的两边、分别与直线交于点、.连接.
甲发现:线段,,之间存在着关系式.
乙发现:的周长是一个恒定不变的值.
丙发现:线段,,之间存在着关系式.
()现请你参与三位同学的研究工作中来,你认为三名同学中哪个的发现是正确的,并说明你的理由.
(十)广雅
24.如图,已知点A(-3,0),二次函数的对称轴为线x=-1,其图象过点A与x
轴交于另一点B,与y轴交于点C.
(1)求二次函数的解析式,写出顶点坐标;
(2)动点M、N同时从B点出发,均以每秒2个单位长度的速度分别沿△ABC的BA、BC边上运动,设其运动的时间为t秒,当其中一个点到达终点时,另一个点也随之停止运动。连结MN,将△BMN沿MN翻折,若点B恰好落在抛物线弧上的B′处,试求t的值及点B′的坐标;
(3)在(2)的条件下,Q为BN的中,,试探究坐标轴上是否存在点P,使得以B、Q、P为顶点的三角形与△ABC相似?如果存在,请求出点P的坐标;如果不存在,试说明理由。
25.如图,在△ABC中,AB=AC=5,,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,连接CE,设BD=x,CE=y.
(1)当⊙P与AB相切时,求⊙P的半径;
(2)当点D在BA的延长线上时,求y关于x的函数解析式,并写出x的取值范围;
(3)在CE的垂直平分线上存在一点O,使得OB=OC,连接OP,当时,求AD的长。
(十一)四中
24.如图1所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=-x²+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-12时,y取最大值254.
(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1:3,求点P的坐标;
(3)直线y=12x+a与(1)中所求的抛物线交于点M、N,两点,问:
①是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.
②猜想当∠MON>90°时,a的取值范围.(不写过程,直接写结论)
25.如图①,已知:在矩形ABCD的边AD上有一点O,OA =3,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.
(1)求证:四边形ABHP是菱形;
(2)问△EFG的直角顶点G能落在⊙O上吗?若能,求出此时x的值;若不能,请说明理由;
(3)求S与x之间的函数关系式,并直接写出FG与⊙O相切时,S的值.
(十二)西关外国语
24、问题探究:在边长为4的正方形ABCD中,对角线AC、BD交于点O.
探究1:如图1,若点P是对角线BD上任意一点,则线段AP的长的取值范围是___;
探究2:如图2,若点P是△ABC内任意一点,点M、N分别是AB边和对角线AC上的两个动点,则当AP的值在探究1中的取值范围内变化时,△PMN的周长是否存在最小值?如果存在,请求出△PMN周长的最小值,若不存在,请说明理由;
问题解决:如图3,在边长为4的正方形ABCD中,点P是△ABC内任意一点,且AP=4,点M、N分别是AB边和对角线AC上的两个动点,则当△PMN的周长取到最小值时,求四边形AMPN面积的最大值。
25、如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到C2,C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
(1)求抛物线C1的解析式及顶点坐标.
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式.
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值.
(十三)南沙区
24.(本小题满分 14 分)如图,已知 AB 为⊙ O 的直径, C 、 D 为⊙ O 上的两点,且
BC = CD = 2,延长 AB 与直线交于点 P ,且 BP = AB ,过点 A 作AF ^ CD ,垂足为 F 。
(1)求证: AD 平分 ÐCAF ;
(2)求 AB 的长度;
(3)求 DF 的长度。
25. (本小题满分 14 分)在平面直角坐标系中,抛物线 y = x 2 + x + 2 与 x 轴交
于 A 、 B 两点( A 在 B 左侧),与 y 轴交于点 C,点 D 的坐标为(2,0),连接 AC 、
CB 、 CD 。
(1)求 DABC的面积;
(2)求证: ÐACO = ÐBCD;
(3) P 是第一象限内抛物线上的一个动点,连接 DP 交 BC 于点 E .
①连接 CP ,当 DCDP的面积最大时,求点 E 的坐标;
②当 DBDE 是等腰三角形时,直接写出点 E 的坐标。
(十四)十六中
24、(14分)已知抛物线交轴于点,交轴于点(点在点的右侧),过点作垂直于直线下方的抛物线上任取一个点,过点作直线平行于轴交直线于点,连接。
(1) 写出三点的坐标;
(2) 若点位于抛物线的对称轴的右侧:
①如果以三点构成的三角形与相似,求出点的坐标;
②若将沿对折,点的对应点为点,是否存在点,使得点落在轴上?若存在,求出点
的坐标;若不存在,请说明理由;
③设的中点是点,其坐标是,请直接写出和的关系式,并写出的取值范围。
19、 (14分)已知菱形的边长为,,等边两边分别交边于点。
(1) 特殊发现:如图,若点分别是边的中点,求证:菱形对角线交点即为等边的外心;
(2) 若点始终分别在边上移动,记等边的外心为点.
①猜想验证:如图,猜想的外心落在哪一直线上,并加以证明;
②拓展运用:如图,当面积最小时,过点任作一直线分别交边于点,交边的延长线于
点,试判断是否为定值,若是,请求出该定值;若不是,请说明理由。
(十五)天河区
24(12分)如图,在中,,以为直径的分别与交于点,过点作的切线,交于点.
(1) 求证:;
(2) 若的半径为,,求阴影部分的面积。
25如图,在平面直角坐标系中,二次函数的图像与轴交于两点,与轴交于点,其对称轴与轴交于点.
(1) 求二次函数的解析式;
(2) 如图1,连接,在线段上是否存在点,使得为等腰三角形?若存在,求出所以符合条件的点的坐标;若不存在,请说明理由;
(3) 如图2,若点是该二次函数图像上的一个动点(其中),连接,求面积的最大值及此时点的坐标。
(十五)天河中学
23.如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点P作BE//AD,交⊙O于点
E,连接ED.
(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且,求△ABC的面积。
24.已知关于的一元二次方程,其中为常数。
(1)求证:无论为何值,方程总有两个不相等实数根;
(2)已知函数的图象不经过第三象限,求的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求的最大整数值。
25.我们把两条中线互相垂真的三角形称为“中垂三角形”。例如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”。设BC=a,
AC=b, AB=c.
(1)特例探索
如图1,当∠ABE=45°,c=时,a=_____,b=________;
如图2,当∠ABE=30°,c=4时,a=_______,b=________;
(2)归纳证明
请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
(3)如图4,在平行四边形ABCD中,点E、F、G分别是AD、BC、CD的中点,BE⊥EG,AD=,AB=3.求AF的长。
26.如图,在平面直角坐标系中,直线与轴交于点A,与轴交于点C,抛物线经过A、C两点,与轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点,
①连BC、CD,设直线线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的橫坐标;若不存在,请说明理由。
(十六)二中
(十七)知用中学
24.(本小题满分14分)
如图11,⊙O是△ABC的内切圆.
(1)若∠A=60°,连接BO、CO并延长,分别交AC、AB于点D、E,
① 求∠BOC的度数;
② 试探究BE、CD、BC之间的等量关系,并证明你的结论;
(2)若AB=AC=10,sin∠ABC=,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.
图11
25.(本小题满分14分)
已知抛物线.
(1)求证:抛物线与轴必定有公共点;
(2)若P(,y1),Q(-2,y2)是抛物线上的两点,且y1y2,求的取值范围;
(3)设抛物线与x轴交于点、,点A在点B的左侧,与y轴负半轴交于点C,且,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,
记△ACE的面积为S1,△DCE的面积为S2,求是否有最值?若有,求出该最值;若没有,请说明理由.
(十八)增城
AC
25.(本题满分 14 分)如图 14,在边长为 2 的正方形 ABCD 中,以点 D 为圆心、 DC 为半径作 ⌒ ,
点 E 在 AB 上,且与 A 、B 两点均不重合,点 M 在 AD 上,且 ME = MD ,过点 E 作 EF ^ ME ,交 BC
于点 F ,连接 DE 、 MF .
(1)求证: EF 是弧AC所在⊙ D 的切线;
(2)当 MA = 时,求 MF 的长;
(3)试判断: DMFE 能否构成等腰直角三角形?
若能,请求出 MF 的长度;若不能,请说明理由.
(十九)育才中学
23(本题满分12分)已知∠ABC及角内一点P
(1)求作:用尺规作图,作∠ABC的平分线BK(保留作图痕迹,不写作法);
(2)请你在∠ABC的平分线BK上找到点M,使点M到∠ABC的两边的距离等于MP,并说明理由。
24.(本题满分14分)
如图,在四边形ABCD中,CB∥AD,∠BCD=90°,CD=4,点E是CD上一点,
(1)已知∠BEA=90°,
①求证:△ADE∽△ECB
②若BE=CD-BC,求△ADE的周长;
(2)已知AB=CD+BC,∠CAD=∠EAC=45°,求△ABE的面积。
25. (本题满分14分)
已知抛物线与x轴交于点A,B(A在B的右侧),与y轴交于点C,∠BAC的平分线AD交y轴与点D,过点D的直线与射线AC,AB分别交于点M,N。
(1)求抛物线的对称轴。
(2)当实数a>-2时,求二次函数在-2<x≤a时的最大值(可用含a的代数式表示)。
(3)当直线绕点D旋转时,试证明为定值,并求出该定值。
(二十)天河省实
24、
25、