中考数学试题压轴题汇编
2010年中考数学试题压轴题汇编(一)
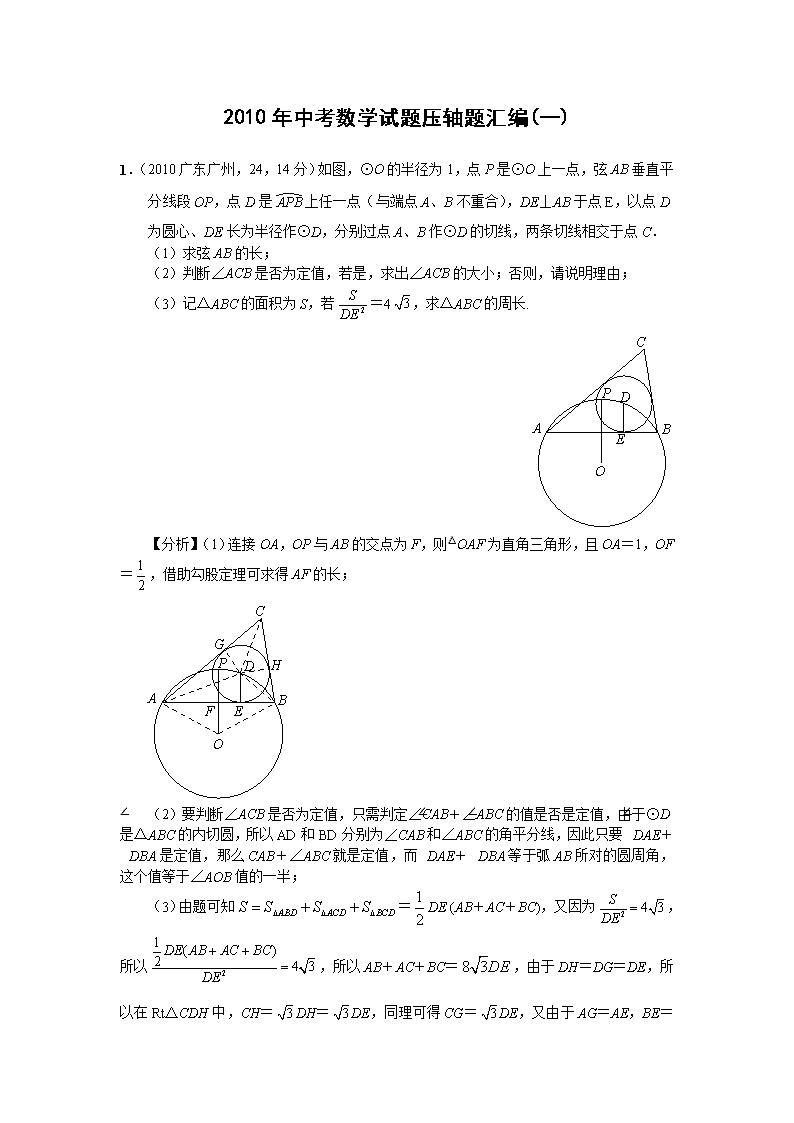
1.(2010广东广州,24,14分)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,若=4,求△ABC的周长.
C
P
D
O
B
A
E
【分析】(1)连接OA,OP与AB的交点为F,则△OAF为直角三角形,且OA=1,OF=,借助勾股定理可求得AF的长;
F
C
P
D
O
B
A
E
H
G
(2)要判断∠ACB是否为定值,只需判定∠CAB+∠ABC的值是否是定值,由于⊙D是△ABC的内切圆,所以AD和BD分别为∠CAB和∠ABC的角平分线,因此只要∠DAE+∠DBA是定值,那么CAB+∠ABC就是定值,而∠DAE+∠DBA等于弧AB所对的圆周角,这个值等于∠AOB值的一半;
(3)由题可知=DE (AB+AC+BC),又因为,所以,所以AB+AC+BC=,由于DH=DG=DE,所以在Rt△CDH中,CH=DH=DE,同理可得CG=DE,又由于AG=AE,BE=
BH,所以AB+AC+BC=CG+CH+AG+AB+BH=DE+,可得=DE+,解得:DE=,代入AB+AC+BC=,即可求得周长为.
【答案】解:(1)连接OA,取OP与AB的交点为F,则有OA=1.
F
C
P
D
O
B
A
E
H
G
∵弦AB垂直平分线段OP,∴OF=OP=,AF=BF.
在Rt△OAF中,∵AF===,∴AB=2AF=.
(2)∠ACB是定值.
理由:由(1)易知,∠AOB=120°,
因为点D为△ABC的内心,所以,连结AD、BD,则∠CAB=2∠DAE,∠CBA=2∠DBA,
因为∠DAE+∠DBA=∠AOB=60°,所以∠CAB+∠CBA=120°,所以∠ACB=60°;
(3)记△ABC的周长为l,取AC,BC与⊙D的切点分别为G,H,连接DG,DC,DH,则有DG=DH=DE,DG⊥AC,DH⊥BC.
∴
=AB•DE+BC•DH+AC•DG=(AB+BC+AC) •DE=l•DE.
∵=4,∴=4,∴l=8DE.
∵CG,CH是⊙D的切线,∴∠GCD=∠ACB=30°,
∴在Rt△CGD中,CG===DE,∴CH=CG=DE.
又由切线长定理可知AG=AE,BH=BE,
∴l=AB+BC+AC=2+2DE=8DE,解得DE=,
∴△ABC的周长为.
【涉及知识点】垂径定理 勾股定理 内切圆 切线长定理 三角形面积
【点评】本题巧妙将垂径定理、勾股定理、内切圆、切线长定理、三角形面积等知识综合在一起,需要考生从前往后按顺序解题,前面问题为后面问题的解决提供思路,是一道难度较大的综合题
2.(2010广东广州,25,14分)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线=-+交折线OAB于点E.
(1)记△ODE的面积为S,求S与的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
C
D
B
A
E
O
【分析】(1)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;②如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积;
(2)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化.
【答案】(1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=
若直线经过点B(3,1)时,则b=
若直线经过点C(0,1)时,则b=1
①若直线与折线OAB的交点在OA上时,即1<b≤,如图25-a,
图1
此时E(2b,0)
∴S=OE·CO=×2b×1=b
②若直线与折线OAB的交点在BA上时,即<b<,如图2
图2
此时E(3,),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[(2b-1)×1+×(5-2b)·()+×3()]=
∴
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
本题答案由无锡市天一实验学校金杨建老师草制!
图3
由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=,DH=1,∴HE=2,
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知:,∴
∴S四边形DNEM=NE·DH=
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为.
【涉及知识点】轴对称 四边形 勾股定理
【点评】本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.
3、(宁波市)如图1、在平面直角坐标系中,O是坐标原点,□ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,),点B在轴的正半轴上,点E为线段AD的中点,过点E的直线与轴交于点F,与射线DC交于点G。
(1)求的度数;
(2)连结OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△,记直线与射线DC的交点为H。
①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;
y
x
C
D
A
O
B
E
G
F
(图1)
x
C
D
A
O
B
E
G
H
F
y
(图2)
x
C
D
A
O
B
E
y
(图3)
②若△EHG的面积为,请直接写出点F的坐标。
解:(1)
(2)(2,)
(3)①略
②过点E作EM⊥直线CD于点M
∵CD∥AB
x
C
D
A
O
B
E
y
(图3)
M
∴
∴
∵
∴
∵△DHE∽△DEG
∴即
当点H在点G的右侧时,设,
∴
解:
∴点F的坐标为(,0)
当点H在点G的左侧时,设,
∴
解:,(舍)
∵△DEG≌△AEF
∴
∵
∴点F的坐标为(,0)
综上可知,点F的坐标有两个,分别是(,0),(,0)
4.(重庆市)已知:如图(1),在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
(1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
(2)在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
(3)如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
解:(1)过点作于点.(如图①)
∵,,
∴.
∵,, ∴.
在Rt中,. (1分)
(ⅰ)当时,,,;
过点作于点.(如图①)
在Rt中,∵,∴,
∴.
即 . (3分)
26题答图②
(ⅱ)当时,(如图②)
,.
∵,,∴.
∴.
即.
故当时,,当时,. (5分)
(2)或或或. (9分)
(3)的周长不发生变化.
26题答图③
延长至点,使,连结.(如图③)
∵,
∴≌.
∴,.…(10分)
∴.
∴.
又∵.
∴≌.∴. (11分)
∴.
∴的周长不变,其周长为4. (12分)
5.(义乌市卷)如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B
(6,3).
(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;
(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示-,并求出当S=36时点A1的坐标;
图2
O1
A1
O
y
x
B1
C1
D
M
C
B
A
O
y
x
图1
D
M
(3)在图1中,设点D坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
解:(1)对称轴:直线…………………………………………………….. 1分
解析式:或…………………………2分
顶点坐标:M(1,)……….……………………………………3分
(2)由题意得
3……………………………….1分
得:①…………….………………….2分
得: ②….………………………………………..……3分
把②代入①并整理得:(S>0) (事实上,更确切为S>6)4分
当时, 解得:(注:S>0或S>6不写不扣 分)
把代入抛物线解析式得 ∴点A1(6,3)………5分
(3)存在………………………………………………………………….….…1分
解法一:易知直线AB的解析式为,可得直线AB与对称轴的
C
B
A
O
y
x
图1-1
D
M
E
P
Q
F
G
交点E的坐标为
∴BD=5,DE=,DP=5-t,DQ= t
当∥时,
得 ………2分
下面分两种情况讨论: 设直线PQ与直线AB、x轴的交点分别为点F、G
①当时,如图1-1 ∵△FQE∽△FAG ∴∠FGA=∠FEQ
∴∠DPQ=∠DEB 易得△DPQ∽△DEB ∴
∴ 得 ∴(舍去)…………………………3分
C
B
A
O
y
x
图1-2
D
M
E
F
P
Q
G
② 当时,如图1-2
∵△FQE∽△FAG ∴∠FAG=∠FQE
∵∠DQP=∠FQE ∠FAG=∠EBD
∴∠DQP=∠DBE 易得△DPQ∽△DEB
∴
∴, ∴
∴当秒时,使直线、直线、轴围成的三角形与直线、直线、抛物线的对称轴围成的三角形相似………………………………4分
解法二:可将向左平移一个单位得到,再用解法一类似的方法可求得
, ,
∴
6.(湖州卷)(本小题12分)如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连结EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
第24题
B
C
A
x
y
F
O
D
E
解:(1)由题意可得A(0,2), B(2,2), C(3,0),
设所求抛物线的解析式为,
则 解得 . ………………..3分
∴ 抛物线的解析式为 . ….……………………..1分
(2)设抛物线的顶点为G,则.过点G作GH⊥AB,垂足为H,
则AH=BH=1,GH=.
∵ EA⊥AB, GH⊥AB, ∴ EA∥GH ,
∴ GH是△EBA的中位线,
∴ . ………………2分
过点B作BM⊥OC,垂足为M,则BM=OA=AB.
∵ ∠EBF=∠ABM=90 º, ∴ ∠EBA=∠FBM=90 º-∠ABF,
∴ Rt△EBA≌Rt△FBM ,∴ .
∵ CM=OC-OM=3-2=1,∴ CF=FM+CM=. …………….2分
(3)设CF=a,则FM=a-1或1- a,
∴BF2= FM2+BM2=(a-1)2+22=a2-2a+5 .
∵△EBA≌△FBM,∴BE=BF.
则, ….1分
又∵, ……….1分
∴,即, ….1分
∴当a=2(在0
PQ时,则点P在线段OC上,
∵ CM∥PQ,CM = 2PQ ,
∴点M纵坐标为点Q纵坐标的2倍,即2 = 2(+1),解得x = 0 ,
∴t = –+ 0 –2 = –2 . --- 2分
2)当CM < PQ时,则点P在OC的延长线上,
∵CM∥PQ,CM = PQ,
∴点Q纵坐标为点M纵坐标的2倍,即+1=2´2,
解得: x = ±. ---2分
当x = –时,得t = –––2 = –8 –,
当x =时, 得t =–8. ---2分
14.(兰州市 本题满分11分)如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线经过坐标原点O和x轴上另一点E(4,0)
(1)当x取何值时,该抛物线的最大值是多少?
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
① 当时,判断点P是否在直线ME上,并说明理由;
② 以P、N、C、D为顶点的多边形面积是否可能为5,若有可能,求出此时N点的坐标;若无可能,请说明理由.
图1 第28题图 图2
解:(1)因抛物线经过坐标原点O(0,0)和点E(4,0)
故可得c=0,b=4
所以抛物线的解析式为…………………………………………1分
由
得当x=2时,该抛物线的最大值是4. …………………………………………2分
(2)① 点P不在直线ME上.
已知M点的坐标为(2,4),E点的坐标为(4,0),
设直线ME的关系式为y=kx+b.
于是得 ,解得
所以直线ME的关系式为y=-2x+8. …………………………………………3分
由已知条件易得,当时,OA=AP=,…………………4分
∵ P点的坐标不满足直线ME的关系式y=-2x+8. [来源:Zxxk.Com]
∴ 当时,点P不在直线ME上. ……………………………………5分
②以P、N、C、D为顶点的多边形面积可能为5
∵ 点A在x轴的非负半轴上,且N在抛物线上,
∴ OA=AP=t.
∴ 点P,N的坐标分别为(t,t)、(t,-t 2+4t) ………………………6分
∴ AN=-t 2+4t (0≤t≤3) ,
∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t
………………………………………………………………………7分
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴ S=DC·AD=×3×2=3.
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=(CD+PN)·AD=[3+(-t 2+3 t)]×2=-t 2+3 t+3……………8分
当-t 2+3 t+3=5时,解得t=1、2………………………………………9分
而1、2都在0≤t≤3范围内,故以P、N、C、D为顶点的多边形面积为5
综上所述,当t=1、2时,以点P,N,C,D为顶点的多边形面积为5,
当t=1时,此时N点的坐标(1,3)………………………………………10分
当t=2时,此时N点的坐标(2,4)………………………………………11分
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.(故在阅卷时没有(ⅰ),只有(ⅱ)也可以,不扣分)
15.(盐城市本题满分12分)已知:函数y=ax2+x+1的图象与x轴只有一个公共点.
(1)求这个函数关系式;
(2)如图所示,设二次函数y=ax2+x+1图象的顶点为B,与y轴的交点为A,P为图象上的一点,若以线段PB为直径的圆与直线AB相切于点B,求P点的坐标;
(3)在(2)中,若圆与x轴另一交点关于直线PB的对称点为M,试探索点M是否在抛物线y=ax2+x+1上,若在抛物线上,求出M点的坐标;若不在,请说明理由.
A
x
y
O
B
1
-2
1
A
x
y
O
B
P
M
C
Q
E
D
解:(1)当a = 0时,y = x+1,图象与x轴只有一个公共点………(1分)
当a≠0时,△=1- 4a=0,a = ,此时,图象与x轴只有一个公共点.
∴函数的解析式为:y=x+1 或`y=x2+x+1……(3分)
(2)设P为二次函数图象上的一点,过点P作PC⊥x
轴于点C.
∵是二次函数,由(1)知该函数关系式为:
y=x2+x+1,则顶点为B(-2,0),图象与y轴的交点
坐标为A(0,1)………(4分)
∵以PB为直径的圆与直线AB相切于点B ∴PB⊥AB 则∠PBC=∠BAO
∴Rt△PCB∽Rt△BOA
∴,故PC=2BC,……………………………………………………(5分)
设P点的坐标为(x,y),∵∠ABO是锐角,∠PBA是直角,∴∠PBO是钝角,∴x<-2
∴BC=-2-x,PC=-4-2x,即y=-4-2x, P点的坐标为(x,-4-2x)
∵点P在二次函数y=x2+x+1的图象上,∴-4-2x=x2+x+1…………………(6分)
解之得:x1=-2,x2=-10
∵x<-2 ∴x=-10,∴P点的坐标为:(-10,16)…………………………………(7分)
(3)点M不在抛物线上……………………………………………
(8分)
由(2)知:C为圆与x 轴的另一交点,连接CM,CM与直线PB的交点为Q,过点M作x轴的垂线,垂足为D,取CD的中点E,连接QE,则CM⊥PB,且CQ=MQ
∴QE∥MD,QE=MD,QE⊥CE
∵CM⊥PB,QE⊥CE PC⊥x 轴 ∴∠QCE=∠EQB=∠CPB
∴tan∠QCE= tan∠EQB= tan∠CPB =
CE=2QE=2×2BE=4BE,又CB=8,故BE=,QE=
∴Q点的坐标为(-,)
可求得M点的坐标为(,)…………………………………………………(11分)
∵=≠
∴C点关于直线PB的对称点M不在抛物线上……………………(12分)
(其它解法,仿此得分)
B
F
A
P
E
O
x
y
(第24题图)
16. (金华卷)如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
(1)过A,B两点的直线解析式是 ▲ ;
(2)当t﹦4时,点P的坐标为 ▲ ;当t ﹦ ▲ ,点P与点E重合;
(3)① 作点P关于直线EF的对称点P′.
在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;若不存在,请说明理由.
解:(1);………4分 (2)(0,),;……4分(各2分)B
F
A
P
E
O
x
y
G
P′
P′
(图1)
(3)①当点在线段上时,过作⊥轴,为垂足(如图1)
∵,,∠∠90°
∴△≌△,∴﹒
又∵,∠60°,∴
B
F
A
P
E
O
x
y
M
P′
H
(图2)
而,∴,
由得 ;…………………1分
当点P在线段上时,形成的是三角形,不存在菱形;
当点P在线段上时,
过P作⊥,⊥,、分别为垂足(如图2)
∵,∴,∴
∴, 又∵
在Rt△中,
即,解得.…………………………………………………1分
B
F
A
P
E
O
x
Q′
B′
Q
C
C1
D1
(图3)
y
②存在﹒理由如下:
∵,∴,,
将△绕点顺时针方向旋转90°,得到
△(如图3)
∵⊥,∴点在直线上,
C点坐标为(,-1)
过作∥,交于点Q,
则△∽△
由,可得Q的坐标为(-,)………………………1
分
根据对称性可得,Q关于直线EF的对称点(-,)也符合条件.……1分
17.( 绍兴市)如图,设抛物线C1:, C2:,C1与C2的交点为A, B,点A的坐标是,点B的横坐标是-2.
第24题图
(1)求的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,
在DH的右侧作正三角形DHG. 记过C2顶点M的
直线为,且与x轴交于点N.
① 若过△DHG的顶点G,点D的坐标为
(1, 2),求点N的横坐标;
② 若与△DHG的边DG相交,求点N的横
坐标的取值范围.
解:(1)∵ 点A在抛物线C1上,∴ 把点A坐标代入得 =1.
∴ 抛物线C1的解析式为,
设B(-2,b), ∴ b=-4, ∴ B(-2,-4) .
(2)①如图1,
∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴ 点M在DH上,MH=5.
过点G作GE⊥DH,垂足为E,
由△DHG是正三角形,可得EG=, EH=1,
第24题图1
∴ ME=4.
设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得 ,
∴ , ∴ ,
∴ 点N的横坐标为.
第24题图2
② 当点D移到与点A重合时,如图2,
直线与DG交于点G,此时点N的横坐标最大.
过点G,M作x轴的垂线,垂足分别为点Q,F,
设N(x,0),
∵ A (2, 4), ∴ G (, 2),
∴ NQ=,NF =, GQ=2, MF =5.
∵ △NGQ∽△NMF,
∴ ,
第24题图3
图4
∴ ,
∴ .
当点D移到与点B重合时,如图3,
直线与DG交于点D,即点B,
此时点N的横坐标最小.
∵ B(-2, -4), ∴ H(-2, 0), D(-2, -4),
设N(x,0),
∵ △BHN∽△MFN, ∴ ,
∴ , ∴ .
∴ 点N横坐标的范围为 ≤x≤.
18. (丽水市卷)△ABC中,∠A=∠B=30°,AB=.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
O
y
x
C
B
A
(第24题)
1
1
-1
-1
(1) 当点B在第一象限,纵坐标是时,求点B的横坐标;
(2) 如果抛物线(a≠0)的对称轴经过点C,请你探究:
① 当,,时,A,B两点是否都
在这条抛物线上?并说明理由;
② 设b=-2am,是否存在这样的m的值,使A,B两点不
可能同时在这条抛物线上?若存在,直接写出m的值;
若不存在,请说明理由.
解:
O
y
x
C
B
A
(甲)
1
1
-1
-1
. ……1分
由此,可求得点C的坐标为(,), ……1分
点A的坐标为(,),
∵ A,B两点关于原点对称,
O
y
x
C
B
A
(乙)
1
1
-1
-1
∴ 点B的坐标为(,).
将点A的横坐标代入(*)式右边,计算得,即等于点A的纵坐标;
将点B的横坐标代入(*)式右边,计算得,即等于点B的纵坐标.
∴ 在这种情况下,A,B两点都在抛物线上. ……2分
情况2:设点C在第四象限(如图乙),则点C的坐标为(,-),
点A的坐标为(,),点B的坐标为(,).
经计算,A,B两点都不在这条抛物线上. ……1分
(情况2另解:经判断,如果A,B两点都在这条抛物线上,那么抛物线将开口向下,而已知的抛物线开口向上.所以A,B两点不可能都在这条抛物线上)
② 存在.m的值是1或-1. ……2分
(,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
19.(益阳市)如图9,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(-2,0),B(6,0),C(0,3).
(1)求经过A、B、C三点的抛物线的解析式;
(2)过C点作CD平行于轴交抛物线于点D,写出D点的坐标,并求AD、BC的交点E的坐标;
(3)若抛物线的顶点为P,连结PC、PD,判断四边形CEDP的形状,并说明理由.
解:⑴ 由于抛物线经过点,可设抛物线的解析式为
,则,
解得
∴抛物线的解析式为 ……………………………4分
⑵ 的坐标为 ……………………………5分
直线的解析式为
直线的解析式为
由
求得交点的坐标为 ……………………………8分
⑶ 连结交于,的坐标为
又∵,
∴,且
∴四边形是菱形 ……………………………12分
20.(丹东市)如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A, 点N的对应点为B, 点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
解:(1) 利用中心对称性质,画出梯形OABC. 1分
∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0) 3分
(写错一个点的坐标扣1分)
O
M
N
H
A
C
E
F
D
B
↑
→
-8
(-6,-4)
x
y
(2)设过A,B,C三点的抛物线关系式为,
∵抛物线过点A(0,4),
∴.则抛物线关系式为. 4分
将B(6,4), C(8,0)两点坐标代入关系式,得
5分
解得 6分
所求抛物线关系式为:. 7分
(3)∵OA=4,OC=8,∴AF=4-m,OE=8-m. 8分
∴
OA(AB+OC)AF·AGOE·OFCE·OA
( 0<<4) 10分
∵. ∴当时,S的取最小值.
又∵0<m<4,∴不存在m值,使S的取得最小值. 12分
(4)当时,GB=GF,当时,BE=BG. 14分
21.(威海市12分)
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.
A
B
D
C
M
N
图 ①
求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
C
图 ②
A
B
D
M
F
E
G
(2)结论应用:
如图③,抛物线的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚
A
图 ③
C
D
B
O
x
y
解:﹙1﹚①证明:分别过点M,N作 ME⊥AB,NF⊥AB,垂足分别为点E,F.
A
B
D
C
M
N
图 ①
E
F
∵ AD∥BC,AD=BC,
∴ 四边形ABCD为平行四边形.
∴ AB∥CD.
∴ ME= NF.
∵S△ABM=,S△ABN=,
∴ S△ABM= S△ABN. ……………………………………………………………………1分
②相等.理由如下:分别过点D,E作DH⊥AB,EK⊥AB,垂足分别为H,K.
H
C
图 ②
A
B
D
M
F
E
G
K
则∠DHA=∠EKB=90°.
∵ AD∥BE,
∴ ∠DAH=∠EBK.
∵ AD=BE,
∴ △DAH≌△EBK.
∴ DH=EK. ……………………………2分
∵ CD∥AB∥EF,
∴S△ABM=,S△ABG=,
∴ S△ABM= S△ABG. …………………………………………………………………3分
﹙2﹚答:存在. …………………………………………………………………………4分
解:因为抛物线的顶点坐标是C(1,4),所以,可设抛物线的表达式为.
又因为抛物线经过点A(3,0),将其坐标代入上式,得,解得.
∴ 该抛物线的表达式为,即. ………………………5分
∴ D点坐标为(0,3).
设直线AD的表达式为,代入点A的坐标,得,解得.
∴ 直线AD的表达式为.
过C点作CG⊥x轴,垂足为G,交AD于点H.则H点的纵坐标为.
∴ CH=CG-HG=4-2=2. …………………………………………………………6分
设点E的横坐标为m,则点E的纵坐标为.
过E点作EF⊥x轴,垂足为F,交AD于点P,则点P的纵坐标为,EF∥CG.
A
图 ③-1
C
D
B
O
x
y
H P
G
F
P
E
由﹙1﹚可知:若EP=CH,则△ADE与△ADC的面积相等.
①若E点在直线AD的上方﹙如图③-1﹚,
则PF=,EF=.
∴ EP=EF-PF==.
∴ .
解得,. ……………………………7分
当时,PF=3-2=1,EF=1+2=3.
∴ E点坐标为(2,3).
同理 当m=1时,E点坐标为(1,4),与C点重合. ………………………………8分
②若E点在直线AD的下方﹙如图③-2,③-3﹚,
则. ……………………………………………9分
∴.解得,. ………………………………10分
当时,E点的纵坐标为;
当时,E点的纵坐标为.
∴ 在抛物线上存在除点C以外的点E,使得△ADE与△ACD的面积相等,E点的坐标为E1(2,3);;. ………………12分
﹙其他解法可酌情处理﹚
A
图③-3
C
D
B
O
x
y
H P
G
F
P
E
A
图③-2
C
D
B
O
x
y
H P
G
F
P
E
22.( 湖北省恩施自治州 12分) 如图11,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POPC, 那么是否存在点P,使四边形POPC为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
图11
解:(1)将B、C两点的坐标代入得 ……………………2分
解得:
所以二次函数的表达式为: ……………………………3分
(2)存在点P,使四边形POPC为菱形.设P点坐标为(x,),
PP交CO于E
若四边形POPC是菱形,则有PC=PO.
连结PP 则PE⊥CO于E,
∴OE=EC=
∴=.…………………6分
∴=
解得=,=(不合题意,舍去)
∴P点的坐标为(,)…………………………8分
(3)过点P作轴的平行线与BC交于点Q,与OB交于点F,设P(x,),
易得,直线BC的解析式为
则Q点的坐标为(x,x-3).
= ……………10分
当时,四边形ABPC的面积最大
此时P点的坐标为,四边形ABPC的
面积. ………………12分
23.(河南省11分)在平面直角坐标系中,已知抛物线经过A,B,C
三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
24.(贵州省遵义市14分)如图,已知抛物线的顶点坐
(27题图)
标为Q,且与轴交于点C,与轴交于A、B两
点(点A在点B的右侧),点P是该抛物线上一动点,从点C
沿抛物线向点A运动(点P与A不重合),过点P作PD∥轴,
交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在问题(2)的结论下,若点E在轴上,点F在抛物线上,
问是否存在以A、P、E、F为顶点的平行四边形?若存在,
求点F的坐标;若不存在,请说明理由.
解:(1)(3分)
∵抛物线的顶点为Q(2,-1)
∴设
将C(0,3)代入上式,得
∴, 即
(2)(7分)分两种情况:
①(3分)当点P1为直角顶点时,点P1与点B重合(如图)
令=0, 得
解之得,
∵点A在点B的右边, ∴B(1,0), A(3,0)
∴P1(1,0)
②(4分)解:当点A为△APD2的直角顶点是(如图)
∵OA=OC, ∠AOC=, ∴∠OAD2=
当∠D2AP2=时, ∠OAP2=, ∴AO平分∠D2AP2
又∵P2D2∥轴, ∴P2D2⊥AO, ∴P2、D2关于轴对称.
设直线AC的函数关系式为
将A(3,0), C(0,3)代入上式得
, ∴
∴
∵D2在上, P2在上,
∴设D2(,), P2(,)
∴()+()=0
, ∴, (舍)
∴当=2时,
==-1
∴P2的坐标为P2(2,-1)(即为抛物线顶点)
∴P点坐标为P1(1,0), P2(2,-1)
(3)(4分)解: 由题(2)知,当点P的坐标为P1(1,0)时,不能构成平行四边形
当点P的坐标为P2(2,-1)(即顶点Q)时,
平移直线AP(如图)交轴于点E,交抛物线于点F.
当AP=FE时,四边形PAFE是平行四边形
∵P(2,-1), ∴可令F(,1)
∴
解之得: ,
∴F点有两点,即F1(,1), F2(,1)
25.(龙岩市14分)如图①,将直角边长为的等腰直角三角形ABC绕其直角顶点C顺时针旋转α角(0°<α<90°),得△A1B1C,A1C交AB于点D,A1B1分别交于BC、AB于点E、F,连接AB1.
(1)求证:△ADC∽△A1DF;
(2)若α=30°,求∠AB1A1的度数;
(3)如图②,当α=45°时,将△A1B1C沿C→A方向平移得△A2B2C2,A2C2交AB于点G,B2C2交BC于点H,设CC2=x(0<x<),△ABC与△A2B2C2的重叠部分面积为S,试求S与x的函数关系式.
图① 图② 备用图
(第25题图)
解:
(1)证明:如图①,根据旋转变换的性质易知
∠CAD=∠FA1D 1分
∵ ∠1=∠2 2分
∴ △ADC∽△A1DF 4分
(2)解:
图①
(法一) ∵ CA=CA1=CB=CB1=
∵ 点A、A1、B、B1均在以C为圆心 半径为的圆上, 2分
∴ ∠AB1A1= 4分
(法二) 如图①,
∵ AC=B1C
∴ ∠4=∠3 1分
∵ ,∠A1CB1=90°
∴ ∠ACB1=120° 2分
∴ ∠4==30° 3分
∴ ∠AB1A1=∠CB1A1∠4=45°30°=15° 4分
(法三)如图①,
∵ AC=B1C
∴ ∠4=∠3 1分
∵ ∠CAB=∠CB1A1
∴ ∠CAB∠3=∠CB1A1∠4
即 ∠B1AB=∠AB1A1 2分
∵ ∠5=∠B1AB+∠AB1A1
∴ ∠5=2∠AB1A1 3分
∵ △ADC∽△A1DF
∴ ∠5=
∴ ∠AB1A1= 4分
(3)解:△A1B1C在平移的过程中,易证得△AC2G、△HB2E、△A2FG、△C2HC、
△FBE均是等腰直角三角形,四边形AC2B2F是平行四边形 1分
∵ AB==2
∴ 当α=45°时,CE=CD=AB=1
情形①:当0<x<1时(如图②所示),
△A2B2C2与△ABC的重叠部分为五边形C2HEFG 2分
(法一) S五边形C2HEFG=S平行四边形AC2B2FSRt△AC2GSRt△HB2E
∵ C2C=x
∴ CH=x,AC2=,B2E=HE=
∴ AG=C2G=AC2=
∴ S平行四边形AC2B2F=AC2·CE=()·1=
图②
SRt△AC2G=·AG2=
SRt△HB2E=·B2E2= 3分
∴ S五边形C2HEFG=
= 4分
(法二) S五边形C2HEFG= SRt△A2B2C2SRt△A2FGSRt△HB2E
∵ C2C=x
∴ AC2=,B2E=
∴ C2G=AC2=
A2G=A2C2C2G =
∴ SRt△A2B2C2=A2==1
SRt△A2FG=A2G2=
SRt△HB2E =B2E2= 3分
∴ S五边形C2HEFG=
= 4分
(法三) S五边形C2HEFG= SRt△ABCSRt△AC2GSRt△C2HCSRt△FBE
∵ C2C=x
∴ AC2=,CH=,BE=
∴ AG=C2G=AC2=
∴ SRt△ABC=A==1
SRt△ AC2G =AG2=
SRt△C2HC =C2C2=
SRt△FBE =BE2= 3分
∴ S五边形C2HEFG=
= 4分
情形②:当1≤x<时(如图③所示),
△A2B2C2与△ABC的重叠部分为直角梯形C2B2FG 5分
(法一) S直角梯形C2B2FG
=S平行四边形C2B2FASRt△AC2G
=AC2·CEAG2
=
= 6分
(法二) S直角梯形C2B2FG
= SRt△A2B2C2SRt△A2FG
图③
=
= 6分
26. (湖南省郴州市)如图(1),抛物线与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线与抛物线交于点B、C.
(1)求点A的坐标;
(2)当b=0时(如图(2)),与的面积大小关系如何?当时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
第26题
图(1)
图(2)
解:
(1)将x=0,代入抛物线解析式,得点A的坐标为(0,-4)………..2分
(2)当b=0时,直线为,由解得,
所以B、C的坐标分别为(-2,-2),(2,2)
,
所以(利用同底等高说明面积相等亦可) ……..4分
当时,仍有成立. 理由如下
由,解得,
所以B、C的坐标分别为(-,-+b),(,+b),
作轴,轴,垂足分别为F、G,则,
而和是同底的两个三角形,
所以. …………………..6分
(3)存在这样的b.
因为
所以
所以,即E为BC的中点
所以当OE=CE时,为直角三角形 …………………..8分
因为
所以 ,而
所以,解得,
所以当b=4或-2时,ΔOBC为直角三角形. ………………….10分
27. (湖南省怀化市本题满分10分)
图9是二次函数的图象,其顶点坐标为M(1,-4).
(1)求出图象与轴的交点A,B的坐标;
图9
(2)在二次函数的图象上是否存在点P,
使,若存在,求出P点的
坐标;若不存在,请说明理由;
(3)将二次函数的图象在轴下方的部分
沿轴翻折,图象的其余部分保持不变,
得到一个新的图象,请你结合这个
新的图象回答:当直线与此
图象有两个公共点时,的取值范围.
解:(1) 因为M(1,-4) 是二次函数的顶点坐标,
所以 ………………………………………2分
令解之得.
∴A,B两点的坐标分别为A(-1,0),B(3,0)………………………………4分
(2) 在二次函数的图象上存在点P,使…………………………5分
设则,又,
∴
图1
∵二次函数的最小值为-4,∴.
当时,.
故P点坐标为(-2,5)或(4,5)……………7分
(3)如图1,当直线经过A点时,可得……………8分
当直线经过B点时,可得…………9分
由图可知符合题意的的取值范围为……10分
28.(湖南省株洲市本题满分10分)在平面直角坐标系中,抛物线过原点O,且与轴交于另一点,其顶点为.孔明同学用一把宽为带刻度的矩形直尺对抛物线进行如下测量:
① 量得;
② 把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图1),测得抛物线与直尺右边的交点的刻度读数为.
请完成下列问题:
(1)写出抛物线的对称轴;
(2)求抛物线的解析式;
(3)将图中的直尺(足够长)沿水平方向向右平移到点的右边(如图2),直尺的两边交轴于点、,交抛物线于点、.求证:.
图1
图2
·
B
解:(1) ……… 2分
(2)设抛物线的解析式为:,当时,,即;当时,,即,依题意得:,解得:.
∴抛物线的解析式为:. ……… 6分
(3)方法一:过点作,垂足为,设, ,得: ①
②
又,得,分别代入①、②得:,
∴
得:
又
∴ ………10分
方法二:过点作,垂足为,设,则,得:
∵
∴ ………10分
2010年中考数学试题压轴题汇编(二)
29.(荆门市本题满分12分)已知:如图一次函数y=x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=x2+bx+c的图象与一次函数y=x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
第24题图
解:(1)将B(0,1),D(1,0)的坐标代入y=x2+bx+c得
得解析式y=x2-x+1……………………………………………………3分
(2)设C(x0,y0),则有
解得∴C(4,3).……………………………………………6分
由图可知:S=S△ACE-S△ABD.又由对称轴为x=可知E(2,0).
∴S=AE·y0-AD×OB=×4×3-×3×1=…………………………………8分
第24题图
当P为直角顶点时,如图:过C作CF⊥x轴于F.
∵Rt△BOP∽Rt△PFC,∴.即.
整理得a2-4a+3=0.解得a=1或a=3
∴所求的点P的坐标为(1,0)或(3,0)
综上所述:满足条件的点P共有二个………………………………………………………12分
(3)设符合条件的点P存在,令P(a,0):
30.(济宁市10分)
如图,在平面直角坐标系中,顶点为(,)的抛物线交轴于点,交轴于,两点(点在点的左侧). 已知点坐标为(,).
(1)求此抛物线的解析式;
(2)过点作线段的垂线交抛物线于点, 如果以点为圆心的圆与直线相切,请判断抛物线的对称轴与⊙有怎样的位置关系,并给出证明;
(第23题)
(3)已知点是抛物线上的一个动点,且位于,两点之间,问:当点运动到什么位置时,的面积最大?并求出此时点的坐标和的最大面积.
解:(1)设抛物线为.
∵抛物线经过点(0,3),∴.∴.
∴抛物线为. ……………………………3分
(2) 答:与⊙相交. …………………………………………………………………4分
证明:当时,,.
∴为(2,0),为(6,0).∴.
设⊙与相切于点,连接,则.
∵,∴.
又∵,∴.∴∽.
∴.∴.∴.…………………………6分
∵抛物线的对称轴为,∴点到的距离为2.
∴抛物线的对称轴与⊙相交. ……………………………………………7分
(第23题)
(3) 解:如图,过点作平行于轴的直线交于点.
可求出的解析式为.…………………………………………8分
设点的坐标为(,),则点的坐标为(,).
∴.
∵,
∴当时,的面积最大为.
此时,点的坐标为(3,). …………………………………………10分
31.(中山市)如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PWQ.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时,△PWQ为直角三角形?当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值.
第22题图(2)
A
B
C
D
F
第22题图(1)
A
B
M
C
F
D
N
W
P
Q
M
N
W
P
Q
32.(青岛市本小题满分12分)已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =
8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
A
D
B
C
F
(
E
)
图(1)
A
D
B
C
F
E
图(2)
P
Q
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
A
B
C
图(3)
解:(1)∵点A在线段PQ的垂直平分线上,
∴AP = AQ.
∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°,
∴∠EQC = 45°.
图(2)
Q
A
D
B
C
F
E
P
M
∴∠DEF =∠EQC.
∴CE = CQ.
由题意知:CE = t,BP =2 t,
∴CQ = t.
∴AQ = 8-t.
在Rt△ABC中,由勾股定理得:AB = 10 cm .
则AP = 10-2 t.
∴10-2 t = 8-t.
解得:t = 2.
答:当t = 2 s时,点A在线段PQ的垂直平分线上. 4分
(2)过P作,交BE于M,
∴.
在Rt△ABC和Rt△BPM中,,
∴ . ∴PM = .
∵BC = 6 cm,CE = t, ∴ BE = 6-t.
∴y = S△ABC-S△BPE =-= -
= = .
∵,∴抛物线开口向上.
∴当t = 3时,y最小=.
答:当t = 3s时,四边形APEC的面积最小,最小面积为cm2. 8分
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作,交AC于N,
C
E
A
D
B
F
图(3)
P
Q
N
∴.
∵,∴△PAN ∽△BAC.
∴.
∴.
∴,.
∵NQ = AQ-AN,
∴NQ = 8-t-() = .
∵∠ACB = 90°,B、C(E)、F在同一条直线上,
∴∠QCF = 90°,∠QCF = ∠PNQ.
∵∠FQC = ∠PQN,
∴△QCF∽△QNP .
∴ . ∴ .
∵ ∴
解得:t = 1.
答:当t = 1s,点P、Q、F三点在同一条直线上. 12分
33、(南充市)已知抛物线上有不同的两点E和F.
(1)求抛物线的解析式.
(2)如图,抛物线与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)当m,n为何值时,∠PMQ的边过点F.
B
A
M
C
D
O
P
Q
x
y
解:(1)抛物线的对称轴为. ……..(1分)
∵ 抛物线上不同两个点E和F的纵坐标相同,
∴ 点E和点F关于抛物线对称轴对称,则 ,且k≠-2.
∴ 抛物线的解析式为. ……..(2分)
(2)抛物线与x轴的交点为A(4,0),与y轴的交点为B(0,4),
∴ AB=,AM=BM=. ……..(3分)
在∠PMQ绕点M在AB同侧旋转过程中,∠MBC=∠DAM=∠PMQ=45°,
在△BCM中,∠BMC+∠BCM+∠MBC=180°,即∠BMC+∠BCM=135°,
在直线AB上,∠BMC+∠PMQ+∠AMD=180°,即∠BMC+∠AMD=135°.
∴ ∠BCM=∠AMD.
故 △BCM∽△AMD. ……..(4分)
∴ ,即 ,.
故n和m之间的函数关系式为(m>0). ……..(5分)
(3)∵ F在上,
∴ ,
化简得,,∴ k1=1,k2=3.
即F1(-2,0)或F2(-4,-8). ……..(6分)
①MF过M(2,2)和F1(-2,0),设MF为,
则 解得, ∴ 直线MF的解析式为.
直线MF与x轴交点为(-2,0),与y轴交点为(0,1).
若MP过点F(-2,0),则n=4-1=3,m=;
若MQ过点F(-2,0),则m=4-(-2)=6,n=. ……..(7分)
②MF过M(2,2)和F1(-4,-8),设MF为,
则 解得, ∴ 直线MF的解析式为.
直线MF与x轴交点为(,0),与y轴交点为(0,).
若MP过点F(-4,-8),则n=4-()=,m=;
若MQ过点F(-4,-8),则m=4-=,n=. ……..(8分)
故当 或时,∠PMQ的边过点F.
34. ((衢州卷)本题12分)
O
y
x
C
B
A
1
1
-1
-1
△ABC中,∠A=∠B=30°,AB=.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
(1) 当点B在第一象限,纵坐标是时,求点B的横坐标;
(2) 如果抛物线(a≠0)的对称轴经过点C,请你探究:
① 当,,时,A,B两点是否都在这条抛物线上?并说明理由;
② 设b=-2am,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
O
y
x
C
B
A
(甲)
1
1
-1
-1
. ……1分
由此,可求得点C的坐标为(,), ……1分
点A的坐标为(,),
∵ A,B两点关于原点对称,
O
y
x
C
B
A
(乙)
1
1
-1
-1
∴ 点B的坐标为(,).
将点A的横坐标代入(*)式右边,计算得,即等于点A的纵坐标;
将点B的横坐标代入(*)式右边,计算得,即等于点B的纵坐标.
∴ 在这种情况下,A,B两点都在抛物线上. ……2分
情况2:设点C在第四象限(如图乙),则点C的坐标为(,-),
解:(1) ∵ 点O是AB的中点, ∴ . ……1分
设点B的横坐标是x(x>0),则, ……1分
解得 ,(舍去).
∴ 点B的横坐标是. ……2分
(2) ① 当,,时,得 ……(*)
. ……1分
以下分两种情况讨论.
情况1:设点C在第一象限(如图甲),则点C的横坐标为,
点A的坐标为(,),点B的坐标为(,).
经计算,A,B两点都不在这条抛物线上. ……1分
(情况2另解:经判断,如果A,B两点都在这条抛物线上,那么抛物线将开口向下,而已知的抛物线开口向上.所以A,B两点不可能都在这条抛物线上)
② 存在.m的值是1或-1. ……2分
(,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
35.(莱芜市本题满分12分)
如图,在平面直角坐标系中,已知抛物线交轴于两点,交轴于点.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线交于点D,作⊙D与x轴相切,⊙D交轴于点E、F两点,求劣弧EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
(第24题图)
x
y
O
A
C
B
D
E
F
解:(1)∵抛物线经过点,,.
∴, 解得.
∴抛物线的解析式为:. …………………………3分
(2)易知抛物线的对称轴是.把x=4代入y=2x得y=8,∴点D的坐标为(4,8).
∵⊙D与x轴相切,∴⊙D的半径为8. …………………………4分
连结DE、DF,作DM⊥y轴,垂足为点M.
在Rt△MFD中,FD=8,MD=4.∴cos∠MDF=.
∴∠MDF=60°,∴∠EDF=120°. …………………………6分
∴劣弧EF的长为:
. …………………………7分
(3)设直线AC的解析式为y=kx+b. ∵直线AC经过点.
∴,解得.∴直线AC的解析式为:. ………8分
设点,PG交直线AC于N,
则点N坐标为.∵.
x
y
O
A
C
B
D
E
F
P
G
N
M
∴①若PN︰GN=1︰2,则PG︰GN=3︰2,PG=GN.
即=.
解得:m1=-3, m2=2(舍去).
当m=-3时,=.
∴此时点P的坐标为. …………………………10分
②若PN︰GN=2︰1,则PG︰GN=3︰1, PG=3GN.
即=.
解得:,(舍去).当时,=.
∴此时点P的坐标为.
综上所述,当点P坐标为或时,△PGA的面积被直线AC分成1︰2两部分. …………………12分
36. (舟山卷 本题12分)△ABC中,∠A=∠B=30°,AB=.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
(1) 当点B在第一象限,纵坐标是时,求点B的横坐标;
(2) 如果抛物线(a≠0)的对称轴经过点C,请你探究:
① 当,,时,A,B两点是否都在这条抛物线上?并说明理由;
② 设b=-2am,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
O
y
x
C
B
A
(第24题)
1
1
-1
-1
解:(1) ∵ 点O是AB的中点, ∴ . ……1分
设点B的横坐标是x(x>0),则, ……1分
解得 ,(舍去).
∴ 点B的横坐标是. ……2分
(2) ① 当,,时,得 ……(*)
. ……1分
以下分两种情况讨论.
情况1:设点C在第一象限(如图甲),则点C的横坐标为,
O
y
x
C
B
A
(甲)
1
1
-1
-1
. ……1分
由此,可求得点C的坐标为(,), ……1分
点A的坐标为(,),
∵ A,B两点关于原点对称,
O
y
x
C
B
A
(乙)
1
1
-1
-1
∴ 点B的坐标为(,).
将点A的横坐标代入(*)式右边,计算得,即等于点A的纵坐标;
将点B的横坐标代入(*)式右边,计算得,即等于点B的纵坐标.
∴ 在这种情况下,A,B两点都在抛物线上. ……2分
情况2:设点C在第四象限(如图乙),则点C的坐标为(,-),
点A的坐标为(,),点B的坐标为(,).
经计算,A,B两点都不在这条抛物线上. ……1分
(情况2另解:经判断,如果A,B两点都在这条抛物线上,那么抛物线将开口向下,而已知的抛物线开口向上.所以A,B两点不可能都在这条抛物线上)
② 存在.m的值是1或-1. ……2分
(,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
37.(2010.十堰)(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
解:(1)分两种情况讨论:
①当m=0 时,方程为x-2=0,∴x=2 方程有实数根
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,∴方程恒有实数根
综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根.
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标.
则有x1+x2=,x1·x2=
由| x1-x2|====,
由| x1-x2|=2得=2,∴=2或=-2
∴m=1或m=
∴所求抛物线的解析式为:y1=x2-2x或y2=x2+2x-
即y1= x(x-2)或y2=(x-2)(x-4)其图象如右图所示.
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围.
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
同理,可得△=9-4(8+3b)=0,得b=-.
观察函数图象可知当b<-或b>-时,直线y=x+b与(2)中的图象只有两个交点.
由
当y1=y2时,有x=2或x=1
当x=1时,y=-1
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上所述可知:当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点.
38.(河北省本小题满分12分)
某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.
若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y =x+150,
成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润 = 销售额-成本-广告费).
若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为
常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费).
(1)当x = 1000时,y = 元/件,w内 = 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
参考公式:抛物线的顶点坐标是.
解:(1)140 57500;
(2)w内 = x(y -20)- 62500 = x2+130 x,
w外 = x2+(150)x.
(3)当x = = 6500时,w内最大;分
由题意得 ,
解得a1 = 30,a2 = 270(不合题意,舍去).所以 a = 30.
(4)当x = 5000时,w内 = 337500, w外 =.
若w内 < w外,则a<32.5;
若w内 = w外,则a = 32.5;
若w内 > w外,则a>32.5.
所以,当10≤ a <32.5时,选择在国外销售;
当a = 32.5时,在国外和国内销售都一样;
当32.5< a ≤40时,选择在国内销售.
39. (德州市本题满分11分)
已知二次函数的图象经过点A(3,0),B(2,-3),C(0,-3).
(1)求此函数的解析式及图象的对称轴;
(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动,点Q从O点出发以相同的速度沿线段OA向A点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.
①当t为何值时,四边形ABPQ为等腰梯形;
x
y
O
A
B
C
P
Q
D
E
G
M
N
F
x
y
O
A
B
C
P
Q
M
N
第23题图
②设PQ与对称轴的交点为M,过M点作x轴的平行线交AB于点N,设四边形ANPQ的面积为S,求面积S关于时间t的函数解析式,并指出t的取值范围;当t为何值时,S有最大值或最小值.
解:(1)∵二次函数的图象经过点C(0,-3),
∴c =-3.
将点A(3,0),B(2,-3)代入得
解得:a=1,b=-2.
∴.-------------------2分
配方得:,所以对称轴为x=1.-------------------3分
(2) 由题意可知:BP= OQ=0.1t.
∵点B,点C的纵坐标相等,
∴BC∥OA.
过点B,点P作BD⊥OA,PE⊥OA,垂足分别为D,E.
要使四边形ABPQ为等腰梯形,只需PQ=AB.
即QE=AD=1.
又QE=OE-OQ=(2-0.1t)-0.1t=2-0.2t,
∴2-0.2t=1.
解得t=5.
即t=5秒时,四边形ABPQ为等腰梯形.-------------------6分
②设对称轴与BC,x轴的交点分别为F,G.
∵对称轴x=1是线段BC的垂直平分线,
∴BF=CF=OG=1.
又∵BP=OQ,
∴PF=QG.
又∵∠PMF=∠QMG,
∴△MFP≌△MGQ.
∴MF=MG.
∴点M为FG的中点 -------------------8分
∴S=,
=.
由=.
.
∴S=.-------------------10分
又BC=2,OA=3,
∴点P运动到点C时停止运动,需要20秒.
∴04.8,x<12,所以.
因此△ABC与正方形DEFG重叠部分的面积为
(0< x≤4.8)
……………………8分
当≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04
当时,因为,所以当时,
△ABC与正方形DEFG重叠部分的面积的最大值为.
因为24>23.04,
所以△ABC与正方形DEFG重叠部分的面积的最大值为24. …10分
C
E
D
G
A
x
y
O
B
F
48.(绵阳市)如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
解:(1)由题意,得 解得,b =-1.
所以抛物线的解析式为,顶点D的坐标为(-1,).
(2)设抛物线的对称轴与x轴交于点M.因为EF垂直平分BC,即C关于直线EG的对称点为B,连结BD交于EF于一点,则这一点为所求点H,使DH + CH最小,即最小为
DH + CH = DH + HB = BD =. 而 .
∴ △CDH的周长最小值为CD + DR + CH =.
设直线BD的解析式为y = k1x + b,则 解得 ,b1 = 3.
所以直线BD的解析式为y =x + 3.
由于BC = 2,CE = BC∕2 =,Rt△CEG∽△COB,
得 CE : CO = CG : CB,所以 CG = 2.5,GO = 1.5.G(0,1.5).
同理可求得直线EF的解析式为y =x +.
联立直线BD与EF的方程,解得使△CDH的周长最小的点H(,).
(3)设K(t,),xF<t<xE.过K作x轴的垂线交EF于N.
则 KN = yK-yN =-(t +)=.
所以 S△EFK = S△KFN + S△KNE =KN(t + 3)+KN(1-t)= 2KN = -t2-3t + 5 =-(t +)2 +.
即当t =-时,△EFK的面积最大,最大面积为,此时K(-,).
49.(钦州市本题满分10分)
如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为 ▲ ;用含t的式子表示点P的坐标为 ▲ ;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
(备用图)
解:(1)(6,4);().(其中写对B点得1分) 3分
(2)∵S△OMP =×OM×, 4分
∴S =×(6 -t)×=+2t.
=(0 < t <6). 6分
∴当时,S有最大值. 7分
(3)存在.
由(2)得:当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),
则直线ON的函数关系式为:.
(备用图)
R2
T1
T2
R1
D2
D1
设点T的坐标为(0,b),则直线MT的函数关系式为:,
解方程组得
∴直线ON与MT的交点R的坐标为.
∵S△OCN =×4×3=6,∴S△ORT = S△OCN =2. 8分
① 当点T在点O、C之间时,分割出的三角形是△OR1T1,如图,作R1D1⊥y轴,D1为垂足,则S△OR1T1=••••RD1•OT =••b=2.
∴, b =.
∴b1 =,b2 =(不合题意,舍去)
此时点T1的坐标为(0,). 9分
② 当点T在OC的延长线上时,分割出的三角形是△R2NE,如图,设MT交CN于点E,由①得点E的横坐标为,作R2D2⊥CN交CN于点D2,则
S△R2NE=•EN•R2D2 =••=2.
∴,b=.
∴b1=,b2=(不合题意,舍去).
∴此时点T2的坐标为(0,).
综上所述,在y轴上存在点T1(0,),T2(0,)符合条件.…10分
50.( 福建省南平市14分)如图1,已知点B(1,3)、C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD.
(1)填空:A点坐标为(____,____),D点坐标为(____,____);
(2)若抛物线y= x2+bx+c经过C、D两点,求抛物线的解析式;
(3)将(2)中的抛物线沿y轴向上平移,设平移后所得抛物线与y轴交点为E,点M是平移后的抛物线与直线AB的公共点,在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.
(提示:抛物线y=ax2+bx+c(a≠0)的对称轴是x=-,顶点坐标是(-,)
O
y
x
A
D
B
C
图1
O
y
x
A
B
C
备用图
·
解:(1) A(-2,0) ,D(-2,3)
(2)∵抛物线y= x2+bx+c 经过C(1,0), D(-2,3)
代入,解得:b=- ,c=
∴ 所求抛物线解析式为:y= x2 - x+
(3) 答:存在
解法一: 设抛物线向上平移H个单位能使EM∥x轴,
则平移后的解析式为:y= x2 - x++h =(x -1)² + h
此时抛物线与y轴交点E(0,+h)
当点M在直线y=x+2上,且满足直线EM∥x轴时
则点M的坐标为()
又 ∵M在平移后的抛物线上,则有
+h=(h--1)²+h
解得: h= 或 h=
(і)当 h= 时,点E(0,2),点M的坐标为(0,2)此时,点E,M重合,不合题意舍去。
(ii)当 h=时,E(0,4)点M的坐标为(2,4)符合题意
综合(i)(ii)可知,抛物线向上平移个单位能使EM∥x轴。
解法二:∵当点M在抛物线对称轴的左侧或在抛物线的顶点时,仅当M,E重合时,它们的纵坐标相等。
∴EM不会与x轴平行
当点M在抛物线的右侧时,设抛物线向上平移H个单位能使EM∥x轴
则平移后的抛物线的解析式为∵y=x²++h =(x - 1)² + h
∴ 抛物线与Y轴交点E(0,+h)
∵抛物线的对称轴为:x=1
根据抛物线的对称性,可知点M的坐标为(2,+h)时,直线EM∥x轴
将(2,+h)代入y=x+2得,+h=2+2 解得:h=
∴ 抛物线向上平移个单位能使EM∥x轴
51. (河池市 本小题满分12分)
如图11,在直角梯形中,∥,,点为坐标原点,点在轴的正半轴上,对角线,相交于点,,.
(1)线段的长为 ,点的坐标为 ;
M
C
B
O
A
图11
(2)求△的面积;
(3)求过,,三点的抛物线的解析式;
(4)若点在(3)的抛物线的对称轴上,点为该
抛物线上的点,且以,,,四点为顶点的四边形
为平行四边形,求点的坐标.
M
C
B
O
A
D
解:(1)4 ;. …………………(2分)
(2)在直角梯形OABC中,OA=AB=4,
∵ ∥ ∴ △OAM∽△BCM ………(3分)
又 ∵ OA=2BC
∴ AM=2CM ,CM=AC ………………(4分)
所以 ………(5分)
(注:另有其它解法同样可得结果,正确得本小题满分.)
(3)设抛物线的解析式为
由抛物线的图象经过点,,.所以
……………………………(6分)
解这个方程组,得,, ………………(7分)
所以抛物线的解析式为 ………………(8分)
(4)∵ 抛物线的对称轴是CD,
① 当点E在轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合,点F的坐标即为点; …(9分)
② 当点E在轴的下方,点F在对称轴的右侧,存在平行四边形,
∥,且,此时点F的横坐标为6,将代入,可得.所以. ………………………………………(11分)
同理,点F在对称轴的左侧,存在平行四边形,∥,且,此时点F的横坐标为,将代入,可得.所以.(12分)
综上所述,点F的坐标为,. ………(12分)
52.(安徽省)如图,已知,相似比为k(k>1),且的三边长分别为a、b、c(a>b>c),的三边长分别为、、.
(1)若c=a1,求证:a=kc;
[证]
(2)若c=a1,试给出符合条件的一对,使得a、b、c和、、都是正整数,并加以说明;
[解]
(3)若b=a1,c=b1,是否存在使得k=2?请说明理由.
[解]
第23题图
解:(1)证:,且相似比为
又 (3分)
(2)解:取 (8分)
此时且 (10分)
注:本题也是开放型的,只要给出的和符合要求就相应赋分.
(3)解:不存在这样的和.理由如下:
若则
又,
(12分)
,而
故不存在这样的和,使得 (14分)
注:本题不要求学生严格按反证法的证明格式推理,只要能说明在题设要求下的情况不可能即可.
53.(芜湖市 本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
解:
(2)设矩形沿直线向右下方翻折后,、的对应点为.
,
.
.
[此时需说明]. 6分
设二次函数解析式为:
抛物线经过、、.
得到解得
. 9分
(3)能,可以在直线上找到点,连接.
由于、在一条直线上,故的和最小,
由于为定长,所以满足周长最小. 10分
设直线的解析式为:
. 12分
. 14分
[注:对于以上各大题的不同解法,解答正确可参照评分!]
54.( 重庆市綦江县) 已知:抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.
(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐标;若不存在请说明理由.
解:方法一:∵抛物线过C(0,-6)
∴c=-6, 即y=ax2+bx-6
由 解得:a= ,b=-
∴该抛物线的解析式为y=x2-x-6 -----------------3分
方法二:∵A、B关于x=2对称
∴A(-8,0) 设y=a(x+8)(x-12)
C在抛物线上 ∴-6=a×8×(-12) 即a=
∴该抛物线的解析式为:y=x2-x-6 --------3分
(2)存在,设直线CD垂直平分PQ,
在Rt△AOC中,AC==10=AD
∴点D在对称轴上,连结DQ 显然∠PDC=∠QDC,-----------4分
由已知∠PDC=∠ACD
∴∠QDC=∠ACD ∴DQ∥AC -----------------------------5分
DB=AB-AD=20-10=10
∴DQ为△ABC的中位线 ∴DQ=AC=5 -----------------6分
AP=AD-PD=AD-DQ=10-5=5
∴t=5÷1=5(秒)
∴存在t=5(秒)时,线段PQ被直线CD垂直平分-----------7分
在Rt△BOC中, BC==6 ∴CQ=3
∴点Q的运动速度为每秒单位长度.------------------8分
(3)存在 过点Q作QH⊥x轴于H,则QH=3,PH=9
在Rt△PQH中,PQ==3 --------------------9分
①当MP=MQ,即M为顶点,
设直线CD的直线方程为:y=kx+b(k≠0),则:
解得:
∴y=3x-6
当x=1时,y=-3 ∴M1(1, -3) ------------------------10分
②当PQ为等腰△MPQ的腰时,且P为顶点.
设直线x=1上存在点M(1,y) ,由勾股定理得:
42+y2=90 即y=±
∴M2(1,) M3(1,-) -----------------------11分
③当PQ为等腰△MPQ的腰时,且Q为顶点.
过点Q作QE⊥y轴于E,交直线x=1于F,则F(1, -3)
设直线x=1存在点M(1,y), 由勾股定理得:
(y+3)2+52=90 即y=-3±
∴M4(1, -3+) M5((1, -3-) --------------------12分
综上所述:存在这样的五点:
M1(1, -3), M2(1,), M3(1,-), M4(1, -3+),
M5((1, -3-).
55.(山东省滨州市 本题满分l0分)
如图,四边形ABCD是菱形,点D的坐标是(0,),以点C为顶点的抛物线恰好经过轴上A、B两点.
(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位?
解:①由抛物线的对称性可知AM=BM
在Rt△AOD和Rt△BMC中,
∵OD=MC,AD=BC,
∴△AOD≌△BMC.
∴OA=MB=MA.………………………………………l分
设菱形的边长为2m,
在Rt△AOD中,
解得m=1. http://www.czsx.com.cn
∴DC=2,OA=1,OB=3.
∴A、B、C三点的坐标分别为(1,0)、(3,0)、(2,)………………… 4分
②设抛物线的解析式为y=(—2)2+
代入A点坐标可得=—
抛物线的解析式为y=—(—2)2+……………………………………7分
③设抛物线的解析式为y=—(一2)2+k
代入D(0,)可得k=5
所以平移后的抛物线的解析式为y=—(一2)2+5…………………………9分
平移了5一=4个单位.…………………………………………………l0分
56.(山东省烟台市 本题满分14分)
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.
解:(1)把A(1,0),B(0,-3)代入y=x2+bx-3a中,得
1+b-3a=0
-3a=-3
a=1
解得
b=2
∴抛物线的解析式为
y=x2+2x-3………………………………………4分
(2)令y=0,得x2+2x-3=0,
解得x1=-3,x2=1
∴点C(-3,0)……………………………………………………5分∵B(0,-3)
∴△BOC为等腰直角三角形.
∴∠CBO=45°……………………………………………………6分过点P作PD⊥y轴,垂足为D,
∵PB⊥BC,∴∠PBD=45°∴PD=BD……………………………8分
所以可设点P(x,-3+x)
则有-3+x=x2+2x-3,∴x=-1,所以P点坐标为(-1,-4)………………………10分
(3)由(2)知,BC⊥BP
当BP为直角梯形一底时,由图象可知点Q不可能在抛物线上.
若BC为直角梯形一底,BP为直角梯形腰时,
∵B(0,-3),C(-3,0),
∴直线BC的解析式为y=-x-3…………………………11分
∵直线PQ∥BC,且P(-1,-4),
∴直线PQ的解析式为y=-(x+1)-3-1
即y=-x-5…………………………………………………12分
y=-x-5
联立方程组得
y=x2+2x-3
解得x1=-1,x2=-2…………………………………………………………………………13分
∴x=-2,y=-3,即点Q(-2,-3)
∴符合条件的点Q的坐标为(-2,-3)………………………………………………14分
57.(四川省成都市)在平面直角坐标系中,抛物线与轴交于两点(点在点的左侧),与轴交于点,点的坐标为,若将经过两点的直线沿轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线.
(1)求直线及抛物线的函数表达式;
(2)如果P是线段上一点,设、的面积分别为、,且,求点P的坐标;
(3)设的半径为l,圆心在抛物线上运动,则在运动过程中是否存在与坐标轴相切的情况?若存在,求出圆心的坐标;若不存在,请说明理由.并探究:若设⊙Q的半径为,圆心在抛物线上运动,则当取何值时,⊙Q与两坐轴同时相切?
解:(1)∵沿轴向下平移3个单位后恰好经过原点,
∴,。
将 代入,得。解得。
∴直线AC的函数表达式为。
∵抛物线的对称轴是直线
∴解得
∴抛物线的函数表达式为。
(2)如图,过点B作BD⊥AC于点D。
∵,
∴
∴。
过点P作PE⊥x轴于点E,
∵PE∥CO,∴△APE∽△ACO,
∴,
∴
∴,解得
∴点P的坐标为
(3)(Ⅰ)假设⊙Q在运动过程中,存在与坐标轴相切的情况。
设点Q的坐标为。
① 当⊙Q与y轴相切时,有,即。
当时,得,∴
当时,得,∴
① 当⊙Q与x轴相切时,有,即
当时,得,即,解得,∴
当时,得,即,解得,∴,。
综上所述,存在符合条件的⊙Q,其圆心Q的坐标分别为,,,,。
(Ⅱ)设点Q的坐标为。
当⊙Q与两坐标轴同时相切时,有。
由,得,即,
∵△=
∴此方程无解。
由,得,即,
解得
∴当⊙Q的半径时,⊙Q与两坐标轴同时相切。
58.(四川省泸州市本题满分l2分)
已二次函数及一次函数.
(l)求该二次函数图象的顶点坐标以及它与轴的交点坐标;
(2)将该二次函数图象在轴下方的部分沿轴翻折到轴上方,图象的其余部分不变,得到一个新图象,请你在图10中画出这个新图象,并求出新图象与直线有三个不同公共点时的值:
(3)当时,函数的图象与轴有两个不同公共点,求的取值范围.
解:(1)二次函数图象的顶点坐标为,与轴的交点坐标为
(2)①当直线位于时,此时过点,
∴,即。
②当直线位于时,此时与函数的图象有一个公共点。
∴方程有一根,
∴,即
当时,满足,
由①②知,或。
(3)∵
∵当时,函数的图象与x轴有两个不同交点,
∴应同时满足下列三方面的条件:
①方程的判别式△=,
②抛物线的对称轴满足,
③当时,函数值,当时,函数值
即,解得。
∴当时,函数图象()的图象与轴有两个不同公共点.
59.( 珠海市)如图,平面直角坐标系中有一矩形ABCD(O为原点),点A、C分别在x轴、y轴上,且C点坐标为(0,6);将BCD沿BD折叠(D点在OC边上),使C点落在OA边的E点上,并将BAE沿BE折叠,恰好使点A落在BD的点F上.
(1)直接写出∠ABE、∠CBD的度数,并求折痕BD所在直线的函数解析式;
(2)过F点作FG⊥x轴,垂足为G,FG的中点为H,若抛物线经过B、H、D三点,求抛物线的函数解析式;
(3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PMMN成立的x的取值范围。
解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(,6) D(0,2)
设BD所在直线的函数解析式是y=kx+b
∴
所以BD所在直线的函数解析式是
(2)∵EF=EA=ABtan30°= ∠FEG=180°-∠FEB-∠AEB=60°
又∵FG⊥OA
∴FG=EFsin60°=3 GE=EFcos60°= OG=OA-AE-GE=
又H为FG中点
∴H(,) …………4分
∵B(,6) 、 D(0,2)、 H(,)在抛物线图象上
∴
∴抛物线的解析式是
(2)∵MP=
MN=6-
H=MP-MN=
由得
该函数简图如图所示:
当00,即HP>MN
60.(山西省)在直角梯形OABC中,CB∥OA,∠COA=90º,CB=3,OA=6,BA=3.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N
.使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
A
B
D
E
(第26题 图1)
F
C
O
M
N
x
y
解:(1)作轴于点则四边形为矩形,
∴ (1分)
∴
在中,
(2分)
∴点的坐标为 (3分)
(2)作轴于点则
∴ (4分)
∴
又∵
∴∴
∴
∴点的坐标为 (5分)
又∵点的坐标为
设直线的解析式为
则解得
∴直线的解析式为 (7分)
(3)答:存在 (8分)
①如图1,当时,四边形为菱形.
作轴于点,则轴,
∴
∴
又∵当时,解得
∴点的坐标为∴
在中,
∴
∴
∴点的坐标为
∴点的坐标为 (10分)
②如图2,当时,四边形为菱形.延长交轴于点则轴.
∵点在直线上,
∴设点坐标为
在中,
∴
解得(舍去),
∴点的坐标为
∴点的坐标为 (12分)
③如图3,当时,四边形为菱形.连接交于点则与互相垂直平分,
∴
∴
∴∴
∴点的坐标为 (14分)
综上所述,轴上方的点有三个,分别为
(其它解法可参照给分).
61.(湖北省襄樊市 本小题满分12分)
如图7,四边形是平行四边形,抛物线过三点,与轴交于另一点.一动点以每秒1个单位长度的速度从点出发沿向点运动,运动到点停止,同时一动点从点出发,以每秒3个单位长度的速度沿向点运动,与点同时停止.
(1)求抛物线的解析式;
(2)若抛物线的对称轴与交于点,与轴交于点,当点运动时间为何值时,四边形是等腰梯形?
图7
(3)当为何值时,以为顶点的三角形与以点为顶点的三角形相似?
解:(1)四边形是平行四边形,
1分
抛物线过点, 2分
由题意,有解得 3分
所求抛物线的解析式为 4分
(2)将抛物线的解析式配方,得
抛物线的对称轴为 5分
欲使四边形为等腰梯形,则有
7分
(3)欲使以点为顶点的三角形与以点为顶点的三角形相似,
有或
即或
①若在轴的同侧.当时,=, 8分
当时,即
解得 9分
②若在轴的异侧.当时,, 10分
当时,,即.解得
.故舍去. 11分
当或或或秒时,以为顶点的三角形与以点
为顶点的三角形相似. 12分