中考数学提高训练（2）

中考数学提高训练（2）

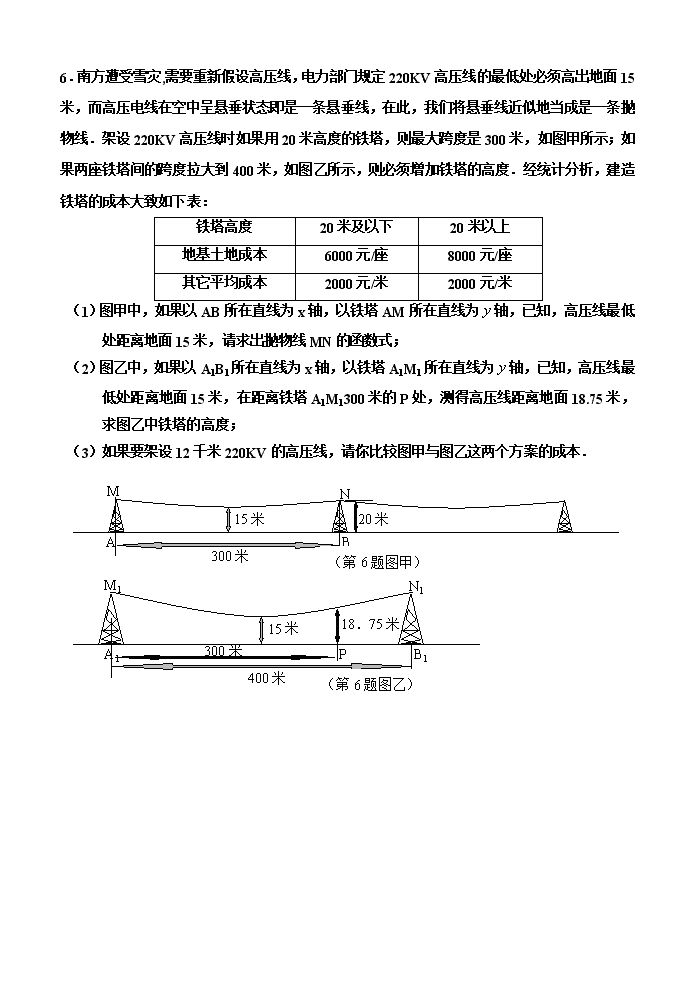
姓名： 第 天中考数学提高训练 实际用时：‎ ‎1．已知：关于x的二次方程的一个根为x=1，且有，求的值。‎ ‎2．用尺规三等分任意角是数学中的一大难题，但我们可以用“折纸法”把一个直角三等分。如图所示，具体做法：‎ ‎（1）将一矩形纸片ABCD对折，EF为折痕；‎ A B C D E G O F ‎（2）继续沿过点C的直线CO对折，使点B落在EF上得到点G，则CO、CG就把∠BCD三等分了。请你写出它的推理过程。‎ ‎3．用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转。当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，通过观察或测量你能找出与BE的长度相等的线段吗？并请说明理由。‎ A B C D E F ‎4．已知二次函数的图象G和x轴有且只有一个交点A，与y轴的交点为 B（0，4），且．‎ ‎⑴求该二次函数的解析表达式；‎ ‎⑵将一次函数y=x的图象作适当平移，使它经过点A，记所得的图象为L，图象L与G的另一个交点为C，求△ABC的面积．‎ ‎5．如图， 四边形OABC为直角梯形，A（4，0），B（3，4），C（0，4）． 点从出发以每秒2个单位长度的速度向运动；点从同时出发，以每秒1个单位长度的速度向运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点作垂直轴于点，连结AC交NP于Q，连结MQ． ‎ ‎（1）点 （填M或N）能到达终点；‎ ‎（2）求△AQM的面积S与运动时间t的函数关系式，并写出自变量t的取值范围，当t为何值时，S的值最大；‎ ‎（3）是否存在点M，使得△AQM为直角三角形？若存在，求出点M的坐标，若不存在，说明理由．‎ ‎6．南方遭受雪灾,需要重新假设高压线，电力部门规定220KV高压线的最低处必须高出地面15米，而高压电线在空中呈悬垂状态即是一条悬垂线，在此，我们将悬垂线近似地当成是一条抛物线．架设220KV高压线时如果用20米高度的铁塔，则最大跨度是300米，如图甲所示；如果两座铁塔间的跨度拉大到400米，如图乙所示，则必须增加铁塔的高度．经统计分析，建造铁塔的成本大致如下表：‎ 铁塔高度 ‎20米及以下 ‎20米以上 地基土地成本 ‎6000元/座 ‎8000元/座 其它平均成本 ‎2000元/米 ‎2000元/米 ‎（1）图甲中，如果以AB所在直线为x轴，以铁塔AM所在直线为轴，已知，高压线最低处距离地面15米，请求出抛物线MN的函数式；‎ ‎（2）图乙中，如果以A1B1所在直线为x轴，以铁塔A1M1所在直线为轴，已知，高压线最低处距离地面15米，在距离铁塔A1M1300米的P处，测得高压线距离地面18.75米，求图乙中铁塔的高度；‎ ‎（3）如果要架设12千米220KV的高压线，请你比较图甲与图乙这两个方案的成本．‎ M1‎ ‎15米 ‎400米 A1‎ B1‎ N1‎ N ‎300米 ‎15米 M A B ‎300米 ‎18．75米 P ‎20米 ‎（第6题图甲）‎ ‎（第23题图甲）‎ ‎（第6题图乙）‎ ‎7．为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若三角板与圆相切且测得PA=‎5cm，求铁环的半径.‎ ‎ B ‎·ｏ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　‎ ‎8．如图，矩形A’BC’O’是矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕B点逆时针旋转得到的．O’点在x轴的正半轴上，B点的坐标为(1，3)．‎ ‎(1)如果二次函数y＝ax2＋bx＋c(a≠0)的图象经过O、O’两点且图象顶点M的纵坐标为—1．求这个二次函数的解析式；‎ ‎(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点P，使得ΔPOM为直角三角形?若存在，请求出P点的坐标和ΔPOM的面积；若不存在，请说明理由；‎ ‎(3)求边C’O’所在直线的解析式．‎ ‎2．在Rt△GFC中FC=BC=GC∴∠FGC=30°‎ ‎∵EF∥DＣ∴∠FGC=∠GCD=30°‎ 又∵折叠∴∠OCB=∠OCG=30°‎ ‎∴CO、CG就把∠BCD三等分了。‎ ‎4.（1）由B（0，4）得，c=4．G与x轴的交点A（，0），由条件，得，所以=，即A（，0）．所以解得所求二次函数的解析式为．‎ A B D C O x y ‎（2）设图象L的函数解析式为y=x+b，因图象L过点A（，0），‎ 所以，即平移后所得一次函数的解析式为 y=． ‎ 令=，‎ 解得，．‎ 将它们分别代入y=，‎ 得，．‎ 所以图象L与G的另一个交点为C（，9）．‎ 如图，过C作CD⊥x轴于D，则 S△ABC=S梯形BCDO-S△ACD -S△ABO ‎==15．‎ ‎5. 解：（1）点 M （2）经过t秒时，， ‎ 则，∵==‎ ‎∴ ∴ ‎ ‎∴‎ ‎ ∴ ∵∴当时，S的值最大． （3）存在． 设经过t秒时，NB=t，OM=2t 则，‎ ‎∴== ‎ ‎①若，则是等腰Rt△底边上的高 ‎∴是底边的中线 ∴‎ ‎∴ ∴ ∴点的坐标为（1，0） ‎ ‎②若，此时与重合 ∴‎ ‎∴ ∴ ∴点的坐标为（2，0）‎ ‎8．‎