中考数学模拟试题及答案

中考数学模拟试题及答案

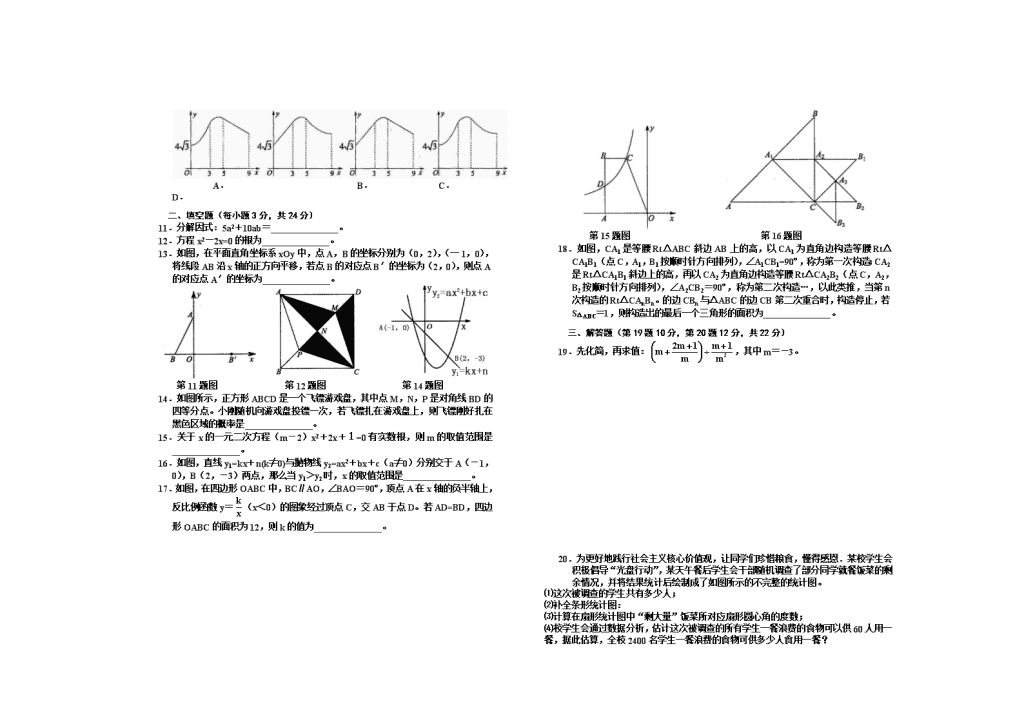
‎2018 年 初 中 升 学 模 拟 考 试（一）‎ 九 年 数 学 试 卷 题 号 一 二 三 四 五 六 七 八 总 分 得 分 ‎（考试时间：120分钟；试卷满分：150分）‎ 温馨提示：请考生把所有的答案都写在答题卡上，写在试卷上不给分，答题要求见答题卡。‎ 一、选择题（每小题3分，共30分）‎ ‎1．－的倒数是 （ ）‎ A．2 B． C．－ D．－2‎ ‎2．科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构，使用此技术测定细菌蛋白结构的分辨率达到0.22纳米，也就是0.000 000 000 22米，将0.000 000 000 22用科学记数法表示为 （ ）‎ A．0.22×l0-9 B．2.2×l0-10 C．22×l0-11 D．0.22×l0-8‎ ‎3．如图是某几何体的三视图，该几何体是 （ ）‎ ‎ A．正方体 B．三棱锥 C．圆柱 D．圆锥 ‎ ‎ ‎ 第3题图 笫4题图 ‎4．如图是根据某地某段时间的每天最低温度绘成的折线图，那么这段时间最低温度的中位数，众数分别是 （ ）‎ ‎ A．4℃，4℃ B．4℃，5℃ C．4.5℃，5℃ D．4.5C，4℃‎ ‎5．不等式组的解集在数轴上可表示为 （ ）‎ ‎6．下列计算，正确的是 （ ）‎ ‎ A．2a2＋a＝3a2 B．2a－1＝(a≠0) C．(－a2)3÷a4＝－a D．2a2·3a3＝6a5‎ ‎7．已知四边形ABCD是平行四边形，下列结论中不正确的是 （ ）‎ ‎ A．当AB＝BC时，它是菱形 B．当AC⊥BD时，它是菱形 ‎ C．当∠ABC＝90º时，它是矩形 D．当AC＝BD时，它是正方形 ‎8．小张承包了一片荒山，他想把这片荒山改造成一个苹果园，现在有一种苹果树苗，它的成活率如下表所示：‎ 移植棵数(n)‎ 成活数(m)‎ 成活率(m/n)‎ 移植棵数(n)‎ 成活数(m)‎ 成活率(m/n)‎ ‎50‎ ‎47‎ ‎0.940‎ ‎1500‎ ‎1335‎ ‎0.890‎ ‎270‎ ‎235‎ ‎0.870‎ ‎3500‎ ‎3203‎ ‎0.915‎ ‎400‎ ‎369‎ ‎0.923‎ ‎7000‎ ‎6335‎ ‎0.905‎ ‎750‎ ‎662‎ ‎0.883‎ ‎14000‎ ‎12628‎ ‎0.902‎ 下面有四个推断：‎ ‎ ①随着移植棵数的增加，树苗成活的频率总在0.900附近摆动，显示出一定的稳定性，可以估计树苗成活的概率是0.900;‎ ‎ ②当移植的棵数是1500时，表格记录成活数是1335，所以这种树苗成活的概率是0.890；‎ ‎ ③若小张移植10000棵这种树苗，则可能成活9000棵；‎ ‎ ④若小张移植20000棵这种树苗，则一定成活18000棵．其中合理的是 （ ）‎ ‎ A．①③ B．①④ C．②③ D．②④‎ ‎9．如图，将矩形ABCD沿着直线BD折叠，使点C落在C′处，P为对角线BD上一点（不与点B，D重合），PM⊥BC′于点M，PN⊥AD于点N。若BD=10，BC=8，则PM+PN的值为 （ ）‎ ‎ A．8 B．6 C．5 D．4.8‎ ‎ ‎ ‎ 第7题图 第8题图 ‎10．如图，在平面直角坐标系中，矩形OABC的顶点A（6，0），C（0，2），过y轴上的点D（0，3），作射线DM与x轴平行，点P，Q分别是射线DM和x轴正半轴上的动点，满足∠PQO＝60º。设点P的横坐标为x（0≤x≤9），△OPQ与矩形OABC的重叠部分的面积为y，则能大致反映y与x函数关系的图象是 （ ）‎ ‎ ‎ ‎ A． B． C． D．‎ 二、填空题（每小题3分，共24分）‎ ‎11．分解因式：5a2＋10ab＝_______________。‎ ‎12．方程x2—2x=0的根为_______________。‎ ‎13．如图，在平面直角坐标系xOy中，点A，B的坐标分别为（0，2），（一1，0），将线段AB沿x轴的正方向平移，若点B的对应点B′的坐标为（2，0），则点A的对应点A′的坐标为_______________。‎ ‎ ‎ 第11题图 第12题图 第14题图 ‎14．如图所示，正方形ABCD是一个飞镖游戏盘，其中点M，N，P是对角线BD的四等分点。小刚随机向游戏盘投镖一次，若飞镖扎在游戏盘上，则飞镖刚好扎在黑色区域的概率是_______________。‎ ‎15．关于x的一元二次方程（m－2）x2＋2x＋１=0有实数根，则m的取值范围是_______________。‎ ‎16．如图，直线y1=kx＋n(k≠0)与抛物线y2=ax2＋bx＋c（a≠0）分别交于A（－1，0），B（2，－3）两点，那么当y1＞y2时，x的取值范围是_______________。‎ ‎17．如图，在四边形OABC中，BC∥AO，∠BAO＝90º，顶点A在x轴的负半轴上，反比例函数y＝（x＜0）的图象经过顶点C，交AB于点D。若AD=BD，四边形OABC的面积为12，则k的值为_______________。‎ ‎ ‎ 第15题图 第16题图 ‎18．如图，CA1是等腰Rt△ABC斜边AB上的高，以CA1为直角边构造等腰Rt△CA1B1（点C，A1，B1按顺时针方向排列），∠A1CB1=90º，称为第一次构造；CA2是Rt△CA1B1斜边上的高，再以CA2为直角边构造等腰Rt△CA2B2（点C，A2，B2按顺时针方向排列），∠A2CB2＝90º，称为第二次构造…，以此类推，当第n次构造的Rt△CAnBn。的边CBn与△ABC的边CB第二次重合时，构造停止，若S△ABC＝1，则构造出的最后一个三角形的面积为_______________。‎ 三、解答题（第19题10分，第20题12分，共22分）‎ ‎19．先化简，再求值：，其中m＝－3。‎ ‎20．为更好地践行社会主义核心价值观，让同学们珍惜粮食，懂得感恩．某校学生会积极倡导“光盘行动”，某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图。‎ ‎⑴这次被调查的学生共有多少人；‎ ‎⑵补全条形统计图：‎ ‎⑶计算在扇形统计图中“剩大量”饭菜所对应扇形圆心角的度数；‎ ‎⑷校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供60人用一餐，据此估算，全校2400名学生一餐浪费的食物可供多少人食用一餐？‎ 四、解答题（每小题12分，共24分）‎ ‎21．如图所示是两张形状、大小相同但是画面不同的图片，把两张图片从中间剪断，再把四张形状相同的小图片（标注a，b，c，d）混合在一起，从四张图片中随机摸取一张，接着再随机摸取一张，则这两张小图片恰好合成一张完整图片的概率是多少？‎ ‎ ‎ ‎ ‎ ‎ a b c d ‎22．如图，港口A在观测站O的正西方向，OA=4km，某船从港口A出发，沿北偏西15º方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏西60º的方向，则该船航行的距离（即AB的长）为多少？（结果保留根号）‎ 五、解答题（12分）‎ ‎23．如图，在△ABC中，∠BAC=90º，点D是△ABC外接⊙O上的点，且＝，连接BD交AC于点E，延长CA到点F，使AF＝AE，连接BF。‎ ‎⑴判断BF与⊙O的位置关系，并说明理由；‎ ‎⑵若EF=12，sin∠C，求DE的长。‎ 六、解答题（12分）‎ ‎24．已知A，B两地有相同数量的某种农产品要出售，A地每吨农产品的售价比B地的少100元，某公司分别用30000元和34000元将这两地的农产品全部购进。‎ ‎⑴求该公司购进农产品的总吨数；‎ ‎⑵该公司打算将购进的这批农产品出售，通过市场调查获悉，当时该农产品的价格为每吨1200元，但随着市场需求的变化，这种农产品的价格每周会上涨200元/吨。公司决定将这批农产品储藏一段时间后再出售，如果这批农产品在储藏过程中，每周会损耗2吨，同时每周还需支付各种费用l600元，那么公司将这批农产品储藏多少周后再出售能获得最大利润？最大利润是多少？‎ ‎（销售利润=销售额－成本－支出费用）‎ 七、解答题（12分）‎ ‎25．已知，在△ABC中，以△ABC的两边BC，AC为斜边向外侧作Rt△BCD和Rt△ACE，使∠CAE=∠CBD，取△ABC边AB的中点M，连接ME，MD。‎ 特例感知：‎ ‎⑴如图1，若AC=BC，∠ACB=60º，∠CAE=∠CBD=45º，取AC，BC的中点F，G，连接MF，MG，EF，DG，则ME与MD的数量关系为_______________，∠EMD＝_______________º；‎ ‎⑵如图2，若∠ACB=90º，∠CAE=∠CBD＝60º，取AC，BC的中点F，G，连接MF，MG，EF，DG，请猜想ME与MD的数量关系以及∠EMD的度数，并给出证明：‎ 类比探究：‎ ‎⑶如图3，当△ABC是任意三角形，∠CAE=∠CBD=α时，连接DE，请猜想△DEM的形状以及∠EMD与α的数量关系，并说明理由。‎ 八、解答题（14分）‎ ‎26．如图，抛物线y=a（x2－7mx＋6m2）（a，m是不为0的常数）与x轴交于A，B两点，与y轴交点C，抛物线过点D（7，3），且对称轴为直线x＝。‎ ‎⑴求抛物线的表达式；‎ ‎⑵点E是对称轴x＝上的动点，连接ED，EB，BD，求△BED周长的最小值；‎ ‎⑶若点P在抛物线上，点Q在x轴上（不与点D重合），当△COB∽△CQP时，求点P，Q的坐标；‎ ‎⑷在⑶的条件下，连接AP，以点A为中心将线段AP旋转，使点P与x轴上的点P′重合，点M是y轴上一点，当直线AM恰好平分∠PAP′时，请直接写出点M的坐标。‎ C九年数学（J营）答案 ‎1．D 2．B 3．D 4．C 5．A 6．D 7．D 8．A 9．B 10．C ‎11．5a(a+2b) 12． 13．（3，） 14． ‎ ‎15．m≤3且m≠2 16．-1＜x＜2 17．－8 18． ‎ ‎0‎ ‎19．解：原式===m(m+1)（或m2+m） ‎ 当m=－3时，原式－3×(－3 +1)=6. ‎ ‎20．（1）这次被调查的同学共有60÷20%=300(人)； ‎ ‎（2）“剩一半”的人数300﹣120﹣60﹣45=75人. ‎ 补充完整如图：‎ ‎（3）因为×360°=54°，所以剩大量饭菜所对应 扇形圆心角的度数是54度. ‎ ‎（4）因为400×=480（人）. 答：略 ‎21．解：用列表法列出两次抽出的小图片的所有可能结果如下：‎ a b c d a ‎（a，b）‎ ‎（a，c）‎ ‎（a，d）‎ b ‎（b，a）‎ ‎（b，c）‎ ‎（b，d）‎ c ‎（c，a）‎ ‎（c，b）‎ ‎（c，d）‎ d ‎（d，a）‎ ‎（d，b）‎ ‎（d，c）‎ 由表格可得，所有可能出现的结果共有12种，每种情况出现的可能性相同，其中抽到的两张小图片恰好合成一张完整图片 的情况有4种，分别是（a，b），（b，a），（d，c），（c，d），所以P（恰好选中乙、丁两队进行比赛）=. ‎ ‎22. 解：如图，过点A作AD⊥OB于D． 由题意知∠AOD=90°—60=30°.‎ 在Rt△AOD中，∵∠ADO=90°，∠AOD=30°，OA=4，‎ ‎∴AD==2． 由题意知∠CAB=90°—15°=75°.‎ 在Rt△ABD中，∵∠ADB=90°，∠B=∠CAB—∠AOB=75°—30°=45°，‎ ‎∴BD=AD=2， ∵Sin45°=, ∴AB==． ‎ ‎23．证明：（1）BF与⊙O相切. ∵∠BAC=90°，∴BD是直径. ∵ ‎ ‎∴∠ABD=∠C=∠D，AB =AD. ∵∠BAC=90°，AF=AE，∴BE=BF. ∴∠ABD=∠ABF.‎ ‎∴∠C=∠ABF. ∵∠ABC+∠C=90°， ∴∠ABC+∠ABF =90°. ∴BC⊥BF，‎ ‎∴BF是⊙O切线. （2）方法1：∵AB=AD，∴BD=2BG.‎ ‎∵∠ABD=∠C, sin∠C ∴sin∠ABD =. ∵AF=AE, EF=12，∴AE =AF=6. ‎ 在Rt△ABE中，∵AE=6，sin∠ABF= BE=10. ∴AB=8. ‎ ‎∴tan∠C=tan∠ABF=. ∴ AC=AB÷tan∠C=8÷=. ‎ ‎∵∠C=∠D，∠CEB=∠DEA, ∴△CEB∽△DEA. ∴ , 即.‎ ‎∴DE. 方法2：过点A作AG⊥BD于点G,(或连接AO交BD于点 G) ‎ ‎∵AB=AD，∴BD=2BG. ∵∠ABD=∠C, sin∠C∴sin∠ABD =.‎ ‎∵AF=AE, EF=12，∴AE =AF=6. 在Rt△ABE中，∵AE=6，sin∠ABF=‎ ‎∴BE=10. ∴AB=8. ∵∠ABD=∠ABD, ∠AGB=∠BAE=90°, ‎ ‎∴△GBA∽△ABE. ∴ ∴BG=. ∴BD=.‎ ‎∴DE=BD－BE=. ‎ ‎24．（1）设公司从A地购进农产品m吨，根据题意， 得=－100. 解得m=40. ‎ 经检验m=40是原方程的根， ∴2m=2×40=80吨 答：公司共购进农产品80吨. ‎ ‎（2）设储存x个星期出售，利润为y元.根据题意， 得y=（1200+200x）（80－2x）－1600x－（30000+34000 ），即y=－400x2 +12000x+32000. ‎ ‎ 将这二次函数配方，得y==－400 （x－15）2+122000. ‎ ‎∵－400＜0,这个二次 函数图象的开口向上，∴y有最大值，‎ ‎∵80－2x≥0，∴ 0≤x≤40 （ 或0＜x＜40） ∴当x=15时，y最大值=122000.‎ 故储存15个星期出售这批农产品可获得利润最大，最大利润是122000元.‎ ‎25．（1） ME=MD， 90 （2）ME=MD，∠EMD=120° 证明：∵F，G，M是△ABC的三边AC， BC，AB的中点，图2 ‎ ∴FM=BC =CG，FM∥BC ，MG=AC=CF ，MG∥AC. ∴∠AFM=∠FMG=∠ACB =∠MGD=90°. ∵∠AEC=∠BDC =90°，F，G图—2‎ 是AC， BC的中点， ∴EF=AF=FC=AC，CG=BG=DG=BC. ∴∠2=∠CEF，∠1=∠CDG，EF= MG，DG= FM. ∴∠3=∠2+∠CEF= 2∠2, ‎ ‎∠4=∠1+∠CDG= 2∠1. ∵∠2+∠EAC=90°，‎ ‎∠1+∠CBD=90°，∠CAE=∠CBD=60°，‎ ‎∴∠1=∠2=30°. ∴∠3=∠4=60°. ‎ ‎∴∠EFM=∠3+∠AFM=150°,∠DGM=∠4+∠CGM=150°‎ ‎∴∠EFM=∠DGM. 又∵EF=MG，FM=DG，‎ ‎∴△MEF≌△DMG. ∴EM=DM，∠EMF=∠MDG. ‎ ‎∵∠EMD=∠FME+∠FMG+∠DMG， ∴∠EMD=∠MDG+∠FMG+∠DMG.‎ ‎∵∠MDG+∠FMG=180°－∠DGM=180°－150°=30°， ∴∠EMD=90°+30°=120° ‎ ‎ (3) △DEM是等腰三角形，∠EMD=2α. ‎ 证明：取AC， BC的中点F，G， 连接MF，MG，EF，DG， ‎ 同（2）证法相同，可证出EF= MG，DG= FM，∠3= 2∠2，∠4= 2∠1.‎ ‎∵∠2+∠EAC=90°，∠1+∠CBD=90°，∠CAE=∠CBD=α，∴∠1=∠2=90°－α. ‎ 图—3‎ ‎∴∠3=∠4=2（90°－α）.‎ ‎ ∴∠EFM=∠3+∠AFM=∠3+∠ACB,∠DGM=∠4+∠CGM=∠4+∠ACB.‎ ‎∴∠EFM=∠DGM. 又∵EF=MG，FM=DG，‎ ‎∴△MEF≌△DMG. ∴EM=DM，∠EMF=∠MDG. ‎ ‎∵∠EMD=∠FME+∠FMG+∠DMG, ‎ 由（2）知∠FMG=∠ACB，‎ ‎∴∠EMD=∠MDG +∠DMG+∠ACB.‎ ‎∵∠MDG+∠DMG =180°－∠DGM ‎=180°－(∠4+∠ACB )= 180°－ 2（90°－α）－∠ACB=2α－∠ACB. ‎ ‎∴∠EMD=2α－∠ACB +∠ACB =2α. ‎ ‎26．（1）方法1: 由题意知，. 解得m=1.‎ ‎ ∵抛物线过点D（7，3）， ∴. ∴a=.‎ ‎∴所求抛物线的表达式为. ‎ 方法2:由题意知，=a(x－m)(x－6m)‎ ‎∴（m+6m）=，则m=1. 则点A(1，0) ，B(6，0). ‎ ‎ ∵抛物线过点D（7，3），∴. ∴a=.‎ ‎∴所求抛物线的表达式为. ‎ ‎（2）过点D作DG⊥x轴于点G,‎ ‎ 在Rt△DBG中，DG=3,BG=7-6=1, ‎ 图—1‎ ‎∴BD=‎ ‎∵C△BED=BD+DE+BE, ‎ ‎∴求C△BED最小值只需满足DE+BE最小即可.‎ ‎∵点C(0,3) ，点D（7，3），‎ ‎∴点C， D关于对称轴x=对称，连接CE，‎ 则CE+BE =DE+BE.‎ 设CB交对称轴x=于点E＇,‎ 由勾股定理,得BC=.‎ ‎∵CE+BE≥CB，即CE+BE≥CE＇+BE＇= DE＇+BE＇,‎ ‎∴DE+BE的最小值就是BC的长. ‎ ‎∴C△BED最小值=+. ‎ ‎（3）如图2, 过点Q作y轴的平行线， 分别过点C，P作直线l的垂线，垂足为点N,H. ‎ 图—2‎ 设点Q的坐标为(n,0) ,‎ ‎∵△COB∽△CQP, ∴. ‎ ‎∠CQP= ∠BOC=90°.‎ 由△CNQ∽△QHP得 ‎∴HQ=2CN=2OQ=－2n, HP=2NQ=2OC=6.‎ 点P的坐标为(6+n, 2n) . ‎ ‎ ∴ .‎ 解得n1=－1,n2=0(舍去).‎ ‎ ∴Q的坐标为(－1,0), 点P的坐标为(5, －2). ‎ ‎（4）点M的坐标为(0，)或(0，).‎ 提示如下：‎ 由题意可得AP=A P＇,MP= M P＇.‎ ‎ 由P (5, －2) , A (1, 0), 得AP=.‎ ‎ ∴A P＇=AP.‎ 图—3‎ 则点P＇坐标为( ,0)或( ,0)‎ ‎ 设点M的坐标为(0,a),‎ 当点P＇坐标为( ,0)时，MP2= P＇M2，，‎ ‎(－2－a)2+52= ()2+a2.解得a=.‎ 当点P＇坐标为( ,0)时，MP2= P＇M2。‎ ‎(－2－a)2+52 = ()2+a2.解得a=.‎ ‎∴点M的坐标为(0，)或(0，). ‎