2020年江苏省常州市中考数学试卷(含解析）

2020年江苏省常州市中考数学试卷(含解析）

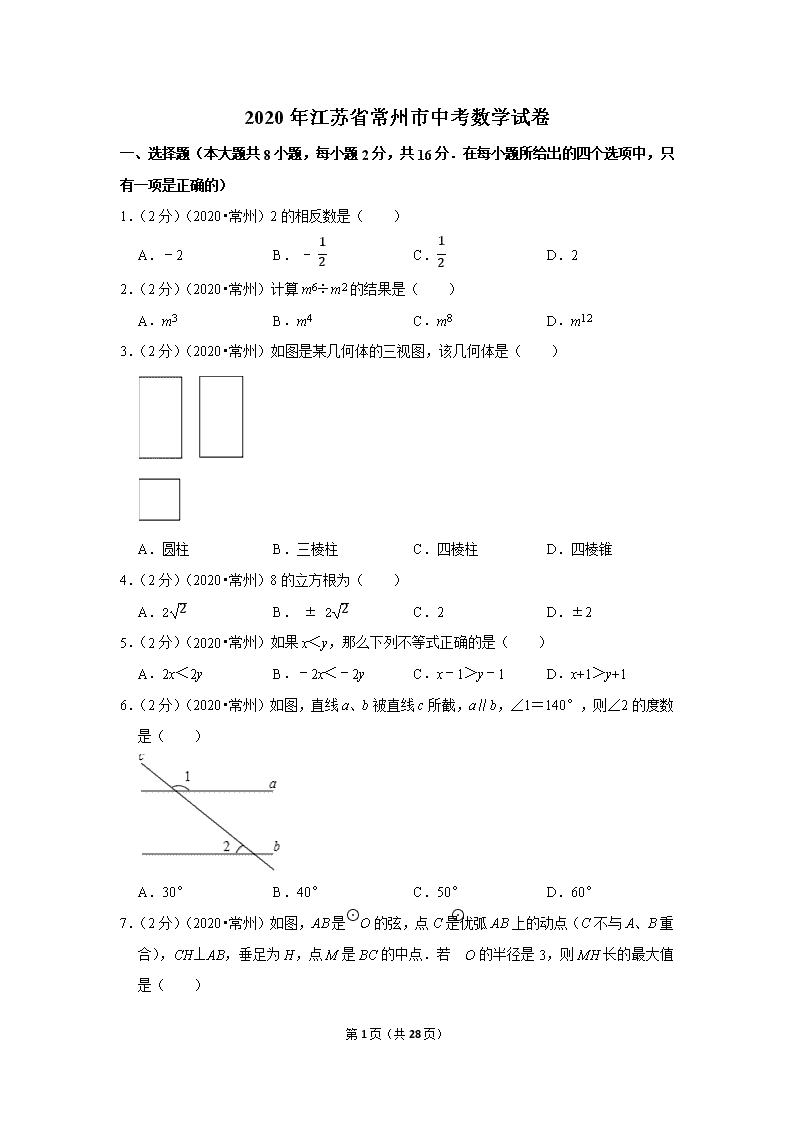
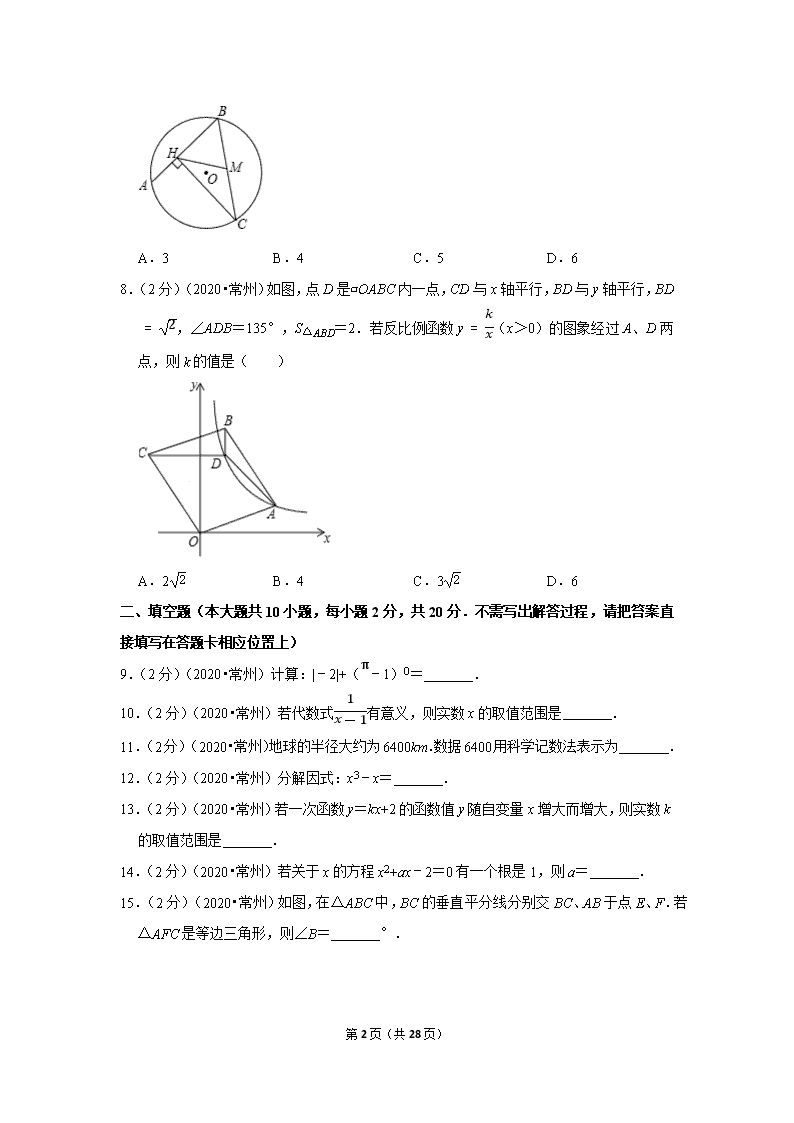
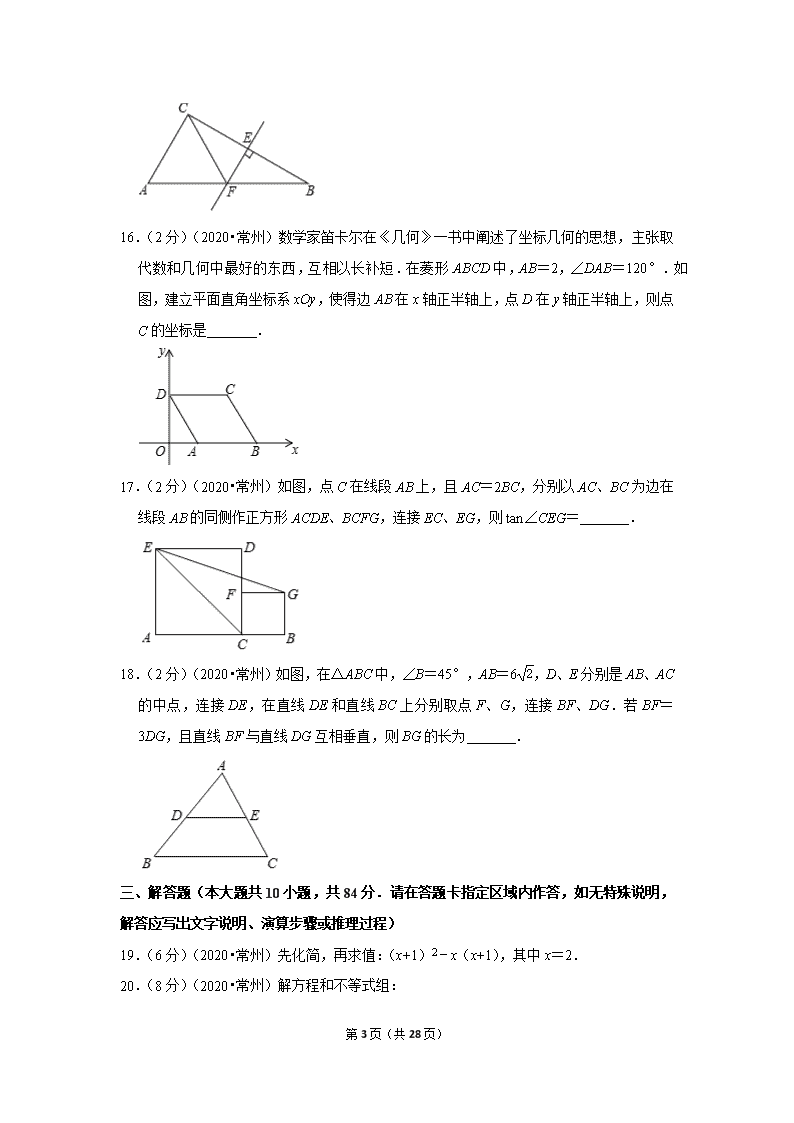
‎2020年江苏省常州市中考数学试卷 一、选择题（本大题共8小题，每小题2分，共16分．在每小题所给出的四个选项中，只有一项是正确的）‎ ‎1．（2分）（2020•常州）2的相反数是（　　）‎ A．﹣2 B．‎-‎‎1‎‎2‎ C．‎1‎‎2‎ D．2‎ ‎2．（2分）（2020•常州）计算m6÷m2的结果是（　　）‎ A．m3 B．m4 C．m8 D．m12‎ ‎3．（2分）（2020•常州）如图是某几何体的三视图，该几何体是（　　）‎ A．圆柱 B．三棱柱 C．四棱柱 D．四棱锥 ‎4．（2分）（2020•常州）8的立方根为（　　）‎ A．‎2‎‎2‎ B．‎±2‎‎2‎ C．2 D．±2‎ ‎5．（2分）（2020•常州）如果x＜y，那么下列不等式正确的是（　　）‎ A．2x＜2y B．﹣2x＜﹣2y C．x﹣1＞y﹣1 D．x+1＞y+1‎ ‎6．（2分）（2020•常州）如图，直线a、b被直线c所截，a∥b，∠1＝140°，则∠2的度数是（　　）‎ A．30° B．40° C．50° D．60°‎ ‎7．（2分）（2020•常州）如图，AB是⊙O的弦，点C是优弧AB上的动点（C不与A、B重合），CH⊥AB，垂足为H，点M是BC的中点．若⊙O的半径是3，则MH长的最大值是（　　）‎ 第28页（共28页）‎ A．3 B．4 C．5 D．6‎ ‎8．（2分）（2020•常州）如图，点D是▱OABC内一点，CD与x轴平行，BD与y轴平行，BD‎=‎‎2‎，∠ADB＝135°，S△ABD＝2．若反比例函数y‎=‎kx（x＞0）的图象经过A、D两点，则k的值是（　　）‎ A．2‎2‎ B．4 C．3‎2‎ D．6‎ 二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把笞案直接填写在答题卡相应位置上）‎ ‎9．（2分）（2020•常州）计算：|﹣2|+（π﹣1）0＝　 　．‎ ‎10．（2分）（2020•常州）若代数式‎1‎x-1‎有意义，则实数x的取值范围是　 　．‎ ‎11．（2分）（2020•常州）地球的半径大约为6400km．数据6400用科学记数法表示为　 　．‎ ‎12．（2分）（2020•常州）分解因式：x3﹣x＝　 　．‎ ‎13．（2分）（2020•常州）若一次函数y＝kx+2的函数值y随自变量x增大而增大，则实数k的取值范围是　 　．‎ ‎14．（2分）（2020•常州）若关于x的方程x2+ax﹣2＝0有一个根是1，则a＝　 　．‎ ‎15．（2分）（2020•常州）如图，在△ABC中，BC的垂直平分线分别交BC、AB于点E、F．若△AFC是等边三角形，则∠B＝　 　°．‎ 第28页（共28页）‎ ‎16．（2分）（2020•常州）数学家笛卡尔在《几何》一书中阐述了坐标几何的思想，主张取代数和几何中最好的东西，互相以长补短．在菱形ABCD中，AB＝2，∠DAB＝120°．如图，建立平面直角坐标系xOy，使得边AB在x轴正半轴上，点D在y轴正半轴上，则点C的坐标是　 　．‎ ‎17．（2分）（2020•常州）如图，点C在线段AB上，且AC＝2BC，分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG，连接EC、EG，则tan∠CEG＝　 　．‎ ‎18．（2分）（2020•常州）如图，在△ABC中，∠B＝45°，AB＝6‎2‎，D、E分别是AB、AC的中点，连接DE，在直线DE和直线BC上分别取点F、G，连接BF、DG．若BF＝3DG，且直线BF与直线DG互相垂直，则BG的长为　 　．‎ 三、解答题（本大题共10小题，共84分．请在答题卡指定区域内作答，如无特殊说明，解答应写出文字说明、演算步骤或推理过程）‎ ‎19．（6分）（2020•常州）先化简，再求值：（x+1）2﹣x（x+1），其中x＝2．‎ ‎20．（8分）（2020•常州）解方程和不等式组：‎ 第28页（共28页）‎ ‎（1）xx-1‎‎+‎2‎‎1-x=‎2；‎ ‎（2）‎2x-6＜0‎‎-3x≤6‎．‎ ‎21．（8分）（2020•常州）为了解某校学生对球类运动的喜爱情况，调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查，并根据调查结果绘制成如图统计图．‎ ‎（1）本次抽样调查的样本容量是　 　；‎ ‎（2）补全条形统计图；‎ ‎（3）该校共有2000名学生，请你估计该校最喜爱“打篮球”的学生人数．‎ ‎22．（8分）（2020•常州）在3张相同的小纸条上分别标上1、2、3这3个号码，做成3支签，放在一个不透明的盒子中．‎ ‎（1）搅匀后从中随机抽出1支签，抽到1号签的概率是　 　；‎ ‎（2）搅匀后先从中随机抽出1支签（不放回），再从余下的2支签中随机抽出1支签，求抽到的2支签上签号的和为奇数的概率．‎ ‎23．（8分）（2020•常州）已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD．‎ ‎（1）求证：∠E＝∠F；‎ ‎（2）若∠A＝40°，∠D＝80°，求∠E的度数．‎ ‎24．（8分）（2020•常州）某水果店销售苹果和梨，购买1千克苹果和3千克梨共需26元，‎ 第28页（共28页）‎ 购买2千克苹果和1千克梨共需22元．‎ ‎（1）求每千克苹果和每千克梨的售价；‎ ‎（2）如果购买苹果和梨共15千克，且总价不超过100元，那么最多购买多少千克苹果？‎ ‎25．（8分）（2020•常州）如图，正比例函数y＝kx的图象与反比例函数y‎=‎‎8‎x（x＞0）的图象交于点A（a，4）．点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交正比例函数的图象于点D．‎ ‎（1）求a的值及正比例函数y＝kx的表达式；‎ ‎（2）若BD＝10，求△ACD的面积．‎ ‎26．（10分）（2020•常州）如图1，点B在线段CE上，Rt△ABC≌Rt△CEF，∠ABC＝∠CEF＝90°，∠BAC＝30°，BC＝1．‎ ‎（1）点F到直线CA的距离是　 　；‎ ‎（2）固定△ABC，将△CEF绕点C按顺时针方向旋转30°，使得CF与CA重合，并停止旋转．‎ ‎①请你在图1中用直尺和圆规画出线段EF经旋转运动所形成的平面图形（用阴影表示，保留画图痕迹，不要求写画法）．该图形的面积为　 　；‎ ‎②如图2，在旋转过程中，线段CF与AB交于点O，当OE＝OB时，求OF的长．‎ ‎27．（10分）（2020•常州）如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为 第28页（共28页）‎ H，且交⊙I于P、Q两点（Q在P、H之间）．我们把点P称为⊙I关于直线a的“远点“，把PQ•PH的值称为⊙I关于直线a的“特征数”．‎ ‎（1）如图2，在平面直角坐标系xOy中，点E的坐标为（0，4）．半径为1的⊙O与两坐标轴交于点A、B、C、D．‎ ‎①过点E画垂直于y轴的直线m，则⊙O关于直线m的“远点”是点　 　（填“A”．“B”、“C”或“D”），⊙O关于直线m的“特征数”为　 　；‎ ‎②若直线n的函数表达式为y‎=‎‎3‎x+4．求⊙O关于直线n的“特征数”；‎ ‎（2）在平面直角坐标系xOy中，直线l经过点M（1，4），点F是坐标平面内一点，以F为圆心，‎2‎为半径作⊙F．若⊙F与直线1相离，点N（﹣1，0）是⊙F关于直线1的“远点”．且⊙F关于直线l的“特征数”是4‎5‎，求直线l的函数表达式．‎ ‎28．（10分）（2020•常州）如图，二次函数y＝x2+bx+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，抛物线过点C（1，0），且顶点为D，连接AC、BC、BD、CD．‎ ‎（1）填空：b＝　 　；‎ ‎（2）点P是抛物线上一点，点P的横坐标大于1，直线PC交直线BD于点Q．若∠CQD＝∠ACB，求点P的坐标；‎ ‎（3）点E在直线AC上，点E关于直线BD对称的点为F，点F关于直线BC对称的点为G，连接AG．当点F在x轴上时，直接写出AG的长．‎ 第28页（共28页）‎ 第28页（共28页）‎ ‎2020年江苏省常州市中考数学试卷 参考答案与试题解析 一、选择题（本大题共8小题，每小题2分，共16分．在每小题所给出的四个选项中，只有一项是正确的）‎ ‎1．（2分）（2020•常州）2的相反数是（　　）‎ A．﹣2 B．‎-‎‎1‎‎2‎ C．‎1‎‎2‎ D．2‎ ‎【解答】解：2的相反数是﹣2．‎ 故选：A．‎ ‎2．（2分）（2020•常州）计算m6÷m2的结果是（　　）‎ A．m3 B．m4 C．m8 D．m12‎ ‎【解答】解：m6÷m2＝m6﹣2＝m4．‎ 故选：B．‎ ‎3．（2分）（2020•常州）如图是某几何体的三视图，该几何体是（　　）‎ A．圆柱 B．三棱柱 C．四棱柱 D．四棱锥 ‎【解答】解：该几何体的主视图为矩形，左视图为矩形，俯视图是一个正方形，‎ 则可得出该几何体是四棱柱．‎ 故选：C．‎ ‎4．（2分）（2020•常州）8的立方根为（　　）‎ A．‎2‎‎2‎ B．‎±2‎‎2‎ C．2 D．±2‎ ‎【解答】解：8的立方根是‎3‎‎8‎‎=‎3‎‎2‎‎3‎=‎2，‎ 故选：C．‎ ‎5．（2分）（2020•常州）如果x＜y，那么下列不等式正确的是（　　）‎ A．2x＜2y B．﹣2x＜﹣2y C．x﹣1＞y﹣1 D．x+1＞y+1‎ ‎【解答】解：A、∵x＜y，‎ 第28页（共28页）‎ ‎∴2x＜2y，故本选项符合题意；‎ B、∵x＜y，‎ ‎∴﹣2x＞﹣2y，故本选项不符合题意；‎ C、∵x＜y，‎ ‎∴x﹣1＜y﹣1，故本选项不符合题意；‎ D、∵x＜y，‎ ‎∴x+1＜y+1，故本选项不符合题意；‎ 故选：A．‎ ‎6．（2分）（2020•常州）如图，直线a、b被直线c所截，a∥b，∠1＝140°，则∠2的度数是（　　）‎ A．30° B．40° C．50° D．60°‎ ‎【解答】解：∵∠1+∠3＝180°，∠1＝40°，‎ ‎∴∠3＝180°﹣∠1＝180°﹣140°＝40°‎ ‎∵a∥b，‎ ‎∴∠2＝∠3＝40°．‎ 故选：B．‎ ‎7．（2分）（2020•常州）如图，AB是⊙O的弦，点C是优弧AB上的动点（C不与A、B重合），CH⊥AB，垂足为H，点M是BC的中点．若⊙O的半径是3，则MH长的最大值是（　　）‎ 第28页（共28页）‎ A．3 B．4 C．5 D．6‎ ‎【解答】解：∵CH⊥AB，垂足为H，‎ ‎∴∠CHB＝90°，‎ ‎∵点M是BC的中点．‎ ‎∴MH‎=‎‎1‎‎2‎BC，‎ ‎∵BC的最大值是直径的长，⊙O的半径是3，‎ ‎∴MH的最大值为3，‎ 故选：A．‎ ‎8．（2分）（2020•常州）如图，点D是▱OABC内一点，CD与x轴平行，BD与y轴平行，BD‎=‎‎2‎，∠ADB＝135°，S△ABD＝2．若反比例函数y‎=‎kx（x＞0）的图象经过A、D两点，则k的值是（　　）‎ A．2‎2‎ B．4 C．3‎2‎ D．6‎ ‎【解答】解：作AM⊥y轴于M，延长BD，交AM于E，设BC与y轴的交点为N，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴OA∥BC，OA＝BC，‎ ‎∴∠AOM＝∠CNM，‎ ‎∵BD∥y轴，‎ ‎∴∠CBD＝∠CNM，‎ 第28页（共28页）‎ ‎∴∠AOM＝∠CBD，‎ ‎∵CD与x轴平行，BD与y轴平行，‎ ‎∴∠CDB＝90°，BE⊥AM，‎ ‎∴∠CDB＝∠AMO，‎ ‎∴△AOM≌△CBD（AAS），‎ ‎∴OM＝BD‎=‎‎2‎，‎ ‎∵S△ABD‎=‎1‎‎2‎BD⋅AE=‎2，BD‎=‎‎2‎，‎ ‎∴AE＝2‎2‎，‎ ‎∵∠ADB＝135°，‎ ‎∴∠ADE＝45°，‎ ‎∴△ADE是等腰直角三角形，‎ ‎∴DE＝AE＝2‎2‎，‎ ‎∴D的纵坐标为3‎2‎，‎ 设A（m，‎2‎），则D（m﹣2‎2‎，3‎2‎），‎ ‎∵反比例函数y‎=‎kx（x＞0）的图象经过A、D两点，‎ ‎∴k‎=‎‎2‎m＝（m﹣2‎2‎）×3‎2‎，‎ 解得m＝3‎2‎，‎ ‎∴k‎=‎‎2‎m＝6．‎ 故选：D．‎ 二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把笞案直接填写在答题卡相应位置上）‎ ‎9．（2分）（2020•常州）计算：|﹣2|+（π﹣1）0＝　3　．‎ ‎【解答】解：|﹣2|+（π﹣1）0‎ 第28页（共28页）‎ ‎＝2+1‎ ‎＝3，‎ 故答案为：3．‎ ‎10．（2分）（2020•常州）若代数式‎1‎x-1‎有意义，则实数x的取值范围是　x≠1　．‎ ‎【解答】解：依题意得：x﹣1≠0，‎ 解得x≠1，‎ 故答案为：x≠1．‎ ‎11．（2分）（2020•常州）地球的半径大约为6400km．数据6400用科学记数法表示为　6.4×103　．‎ ‎【解答】解：将6400用科学记数法表示为6.4×103．‎ 故答案为：6.4×103．‎ ‎12．（2分）（2020•常州）分解因式：x3﹣x＝　x（x+1）（x﹣1）　．‎ ‎【解答】解：x3﹣x，‎ ‎＝x（x2﹣1），‎ ‎＝x（x+1）（x﹣1）．‎ 故答案为：x（x+1）（x﹣1）．‎ ‎13．（2分）（2020•常州）若一次函数y＝kx+2的函数值y随自变量x增大而增大，则实数k的取值范围是　k＞0　．‎ ‎【解答】解：∵一次函数y＝kx+2，函数值y随x的值增大而增大，‎ ‎∴k＞0．‎ 故答案为：k＞0．‎ ‎14．（2分）（2020•常州）若关于x的方程x2+ax﹣2＝0有一个根是1，则a＝　1　．‎ ‎【解答】解：∵关于x的方程x2+ax﹣2＝0有一个根是1，‎ ‎∴把x＝1代入方程得：1+a﹣2＝0，‎ 解得：a＝1，‎ 故答案为：1．‎ ‎15．（2分）（2020•常州）如图，在△ABC中，BC的垂直平分线分别交BC、AB于点E、F．若△AFC是等边三角形，则∠B＝　30　°．‎ 第28页（共28页）‎ ‎【解答】解：∵EF垂直平分BC，‎ ‎∴BF＝CF，‎ ‎∴∠B＝∠BCF，‎ ‎∵△ACF为等边三角形，‎ ‎∴∠AFC＝60°，‎ ‎∴∠B＝∠BCF＝30°．‎ 故答案为：30．‎ ‎16．（2分）（2020•常州）数学家笛卡尔在《几何》一书中阐述了坐标几何的思想，主张取代数和几何中最好的东西，互相以长补短．在菱形ABCD中，AB＝2，∠DAB＝120°．如图，建立平面直角坐标系xOy，使得边AB在x轴正半轴上，点D在y轴正半轴上，则点C的坐标是　（2，‎3‎）　．‎ ‎【解答】解：∵四边形ABCD是菱形，且AB＝2，‎ ‎∴CD＝AD＝AB＝2，‎ ‎∵∠DAB＝120°，‎ ‎∴∠OAD＝60°，‎ Rt△AOD中，∠ADO＝30°，‎ ‎∴OA‎=‎‎1‎‎2‎AD‎=‎1‎‎2‎×2=‎1，OD‎=‎2‎‎2‎‎-‎‎1‎‎2‎=‎‎3‎，‎ ‎∴C（2，‎3‎），‎ 故答案为：（2，‎3‎）．‎ ‎17．（2分）（2020•常州）如图，点C在线段AB上，且AC＝2BC，分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG，连接EC、EG，则tan∠CEG＝　‎1‎‎2‎　．‎ 第28页（共28页）‎ ‎【解答】解：连接CG，‎ 在正方形ACDE、BCFG中，‎ ‎∠ECA＝∠GCB＝45°，‎ ‎∴∠ECG＝90°，‎ 设AC＝2，BC＝1，‎ ‎∴CE＝2‎2‎，CG‎=‎‎2‎，‎ ‎∴tan∠GEC‎=CGEC=‎‎1‎‎2‎，‎ 故答案为：‎1‎‎2‎．‎ ‎18．（2分）（2020•常州）如图，在△ABC中，∠B＝45°，AB＝6‎2‎，D、E分别是AB、AC的中点，连接DE，在直线DE和直线BC上分别取点F、G，连接BF、DG．若BF＝3DG，且直线BF与直线DG互相垂直，则BG的长为　4或2　．‎ ‎【解答】解：如图，过点B作BT⊥BF交ED的延长线于T，过点B作BH⊥DT于H．‎ ‎∵DG⊥BF，BT⊥BF，‎ 第28页（共28页）‎ ‎∴DG∥BT，‎ ‎∵AD＝DB，AE＝EC，‎ ‎∴DE∥BC，‎ ‎∴四边形DGBT是平行四边形，‎ ‎∴BG＝DT，DG＝BT，∠BDH＝∠ABC＝45°，‎ ‎∵AD＝DB＝3‎2‎，‎ ‎∴BH＝DH＝3，‎ ‎∵∠TBF＝∠BHF＝90°，‎ ‎∴∠TBH+∠FBH＝90°，∠FBH+∠F＝90°，‎ ‎∴∠TBH＝∠F，‎ ‎∴tan∠F＝tan∠TBH‎=BTBF=DGBF=‎‎1‎‎3‎，‎ ‎∴THBH‎=‎‎1‎‎3‎，‎ ‎∴TH＝1，‎ ‎∴DT＝TH+DH＝1+3＝4，‎ ‎∴BG＝4．‎ 当点F在ED的延长线上时，同法可得DT＝BG＝3﹣1＝2．‎ 故答案为4或2．‎ 三、解答题（本大题共10小题，共84分．请在答题卡指定区域内作答，如无特殊说明，解答应写出文字说明、演算步骤或推理过程）‎ ‎19．（6分）（2020•常州）先化简，再求值：（x+1）2﹣x（x+1），其中x＝2．‎ ‎【解答】解：（x+1）2﹣x（x+1）‎ ‎＝x2+2x+1﹣x2﹣x ‎＝x+1，‎ 当x＝2时，原式＝2+1＝3．‎ 第28页（共28页）‎ ‎20．（8分）（2020•常州）解方程和不等式组：‎ ‎（1）xx-1‎‎+‎2‎‎1-x=‎2；‎ ‎（2）‎2x-6＜0‎‎-3x≤6‎．‎ ‎【解答】解：（1）方程两边都乘以x﹣1得：x﹣2＝2（x﹣1），‎ 解得：x＝0，‎ 检验：把x＝0代入x﹣1得：x﹣1≠0，‎ 所以x＝0是原方程的解，‎ 即原方程的解是：x＝0；‎ ‎（2）‎2x-6＜0①‎‎-3x≤6②‎，‎ ‎∵解不等式①得：x＜3，‎ 解不等式②得：x≥﹣2，‎ ‎∴不等式组的解集是：﹣2≤x＜3．‎ ‎21．（8分）（2020•常州）为了解某校学生对球类运动的喜爱情况，调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查，并根据调查结果绘制成如图统计图．‎ ‎（1）本次抽样调查的样本容量是　100　；‎ ‎（2）补全条形统计图；‎ ‎（3）该校共有2000名学生，请你估计该校最喜爱“打篮球”的学生人数．‎ ‎【解答】解：（1）本次抽样调查的总人数是：25÷25%＝100（人），‎ 则样本容量是100；‎ 第28页（共28页）‎ 故答案为：100；‎ ‎（2）打乒乓球的人数有：100×35%＝35（人），‎ 踢足球的人数有：100﹣25﹣35﹣15＝25（人），补全统计图如下：‎ ‎（3）根据题意得：‎ ‎2000‎×‎15‎‎100‎=‎300（人），‎ 答：估计该校最喜爱“打篮球”的学生人数有300人．‎ ‎22．（8分）（2020•常州）在3张相同的小纸条上分别标上1、2、3这3个号码，做成3支签，放在一个不透明的盒子中．‎ ‎（1）搅匀后从中随机抽出1支签，抽到1号签的概率是　‎1‎‎3‎　；‎ ‎（2）搅匀后先从中随机抽出1支签（不放回），再从余下的2支签中随机抽出1支签，求抽到的2支签上签号的和为奇数的概率．‎ ‎【解答】解：（1）共有3种可能出现的结果，其中“抽到1号”的有1种，因此“抽到1号”的概率为‎1‎‎3‎，‎ 故答案为：‎1‎‎3‎；‎ ‎（2）用列表法表示所有可能出现的结果情况如下：‎ 第28页（共28页）‎ 共有6种可能出现的结果，其中“和为奇数”的有4种，‎ ‎∴P（和为奇数）‎=‎4‎‎6‎=‎‎2‎‎3‎．‎ ‎23．（8分）（2020•常州）已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD．‎ ‎（1）求证：∠E＝∠F；‎ ‎（2）若∠A＝40°，∠D＝80°，求∠E的度数．‎ ‎【解答】证明：（1）∵EA∥FB，‎ ‎∴∠A＝∠FBD，‎ ‎∵AB＝CD，‎ ‎∴AB+BC＝CD+BC，‎ 即AC＝BD，‎ 在△EAC与△FBD中，‎ EA=FB‎∠A=∠FBDAC=BD‎，‎ ‎∴△EAC≌△FBD（SAS），‎ ‎∴∠E＝∠F；‎ ‎（2）∵△EAC≌△FBD，‎ ‎∴∠ECA＝∠D＝80°，‎ ‎∵∠A＝40°，‎ ‎∴∠E＝180°﹣40°﹣80°＝60°，‎ 答：∠E的度数为60°．‎ ‎24．（8分）（2020•常州）某水果店销售苹果和梨，购买1千克苹果和3千克梨共需26元，购买2千克苹果和1千克梨共需22元．‎ ‎（1）求每千克苹果和每千克梨的售价；‎ ‎（2）如果购买苹果和梨共15千克，且总价不超过100元，那么最多购买多少千克苹果？‎ ‎【解答】解：（1）设每千克苹果的售价为x元，每千克梨的售价为y元，‎ 第28页（共28页）‎ 依题意，得：x+3y=26‎‎2x+y=22‎，‎ 解得：x=8‎y=6‎．‎ 答：每千克苹果的售价为8元，每千克梨的售价为6元．‎ ‎（2）设购买m千克苹果，则购买（15﹣m）千克梨，‎ 依题意，得：8m+6（15﹣m）≤100，‎ 解得：m≤5．‎ 答：最多购买5千克苹果．‎ ‎25．（8分）（2020•常州）如图，正比例函数y＝kx的图象与反比例函数y‎=‎‎8‎x（x＞0）的图象交于点A（a，4）．点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交正比例函数的图象于点D．‎ ‎（1）求a的值及正比例函数y＝kx的表达式；‎ ‎（2）若BD＝10，求△ACD的面积．‎ ‎【解答】解：（1）把点A（a，4）代入反比例函数y‎=‎‎8‎x（x＞0）得，‎ a‎=‎8‎‎4‎=‎2，‎ ‎∴点A（2，4），代入y＝kx得，k＝2，‎ ‎∴正比例函数的关系式为y＝2x，‎ 答：a＝2，正比例函数的关系式为y＝2x；‎ ‎（2）当BD＝10＝y时，代入y＝2x得，x＝5，‎ ‎∴OB＝5，‎ 当x＝5代入y‎=‎‎8‎x得，y‎=‎‎8‎‎5‎，即BC‎=‎‎8‎‎5‎，‎ ‎∴CD＝BD﹣BC＝10‎-‎8‎‎5‎=‎‎42‎‎5‎，‎ 第28页（共28页）‎ ‎∴S△ACD‎=‎1‎‎2‎×‎42‎‎5‎×‎（5﹣2）＝12.6，‎ ‎26．（10分）（2020•常州）如图1，点B在线段CE上，Rt△ABC≌Rt△CEF，∠ABC＝∠CEF＝90°，∠BAC＝30°，BC＝1．‎ ‎（1）点F到直线CA的距离是　1　；‎ ‎（2）固定△ABC，将△CEF绕点C按顺时针方向旋转30°，使得CF与CA重合，并停止旋转．‎ ‎①请你在图1中用直尺和圆规画出线段EF经旋转运动所形成的平面图形（用阴影表示，保留画图痕迹，不要求写画法）．该图形的面积为　π‎12‎　；‎ ‎②如图2，在旋转过程中，线段CF与AB交于点O，当OE＝OB时，求OF的长．‎ ‎【解答】解：（1）如图1中，作FD⊥AC于D，‎ ‎∵Rt△ABC≌Rt△CEF，∠ABC＝∠CEF＝90°，∠BAC＝30°，BC＝1．‎ ‎∴∠ACB＝60°，∠FCE＝∠BAC＝30°，AC＝CF，‎ ‎∴∠ACF＝30°，‎ ‎∴∠BAC＝∠FCD，‎ 在△ABC和△CDF中，‎ ‎∠BAC=∠FCD‎∠ABC=∠CDFAC=CF‎，‎ 第28页（共28页）‎ ‎∴△ABC≌△CDF（AAS），‎ ‎∴FD＝BC＝1，‎ 故答案为1；‎ ‎（2）线段EF经旋转运动所形成的平面图形如图所示，此时点E落在CF上的点H处．‎ S阴＝S△EFC+S扇形ACF﹣S扇形CEH﹣S△AHC＝S扇形ACF﹣S扇形ECH‎=‎30⋅π⋅‎‎2‎‎2‎‎360‎-‎30⋅π⋅(‎‎3‎‎)‎‎2‎‎360‎=‎π‎12‎．‎ 故答案为π‎12‎．‎ ‎（3）如图2中，过点E作EH⊥CF于H．设OB＝OE＝x．‎ 在Rt△ECF中，∵EF＝1，∠ECF＝30°，EH⊥CF，‎ ‎∴EC‎=‎‎3‎EF‎=‎‎3‎，EH‎=‎‎3‎‎2‎，CH‎=‎‎3‎EH‎=‎‎3‎‎2‎，‎ 在Rt△BOC中，OC‎=OB‎2‎+BC‎2‎=‎‎1+‎x‎2‎，‎ ‎∴OH＝CH﹣OC‎=‎3‎‎2‎-‎‎1+‎x‎2‎，‎ 在Rt△EOH中，则有x2＝（‎3‎‎2‎）2+（‎3‎‎2‎‎-‎‎1+‎x‎2‎）2，‎ 第28页（共28页）‎ 解得x‎=‎‎7‎‎3‎或‎-‎‎7‎‎3‎（不合题意舍弃），‎ ‎∴OC‎=‎1+(‎‎7‎‎3‎‎)‎‎2‎=‎‎4‎‎3‎，‎ ‎∵CF＝2EF＝2，‎ ‎∴OF＝CF﹣OC＝2‎-‎4‎‎3‎=‎‎2‎‎3‎．‎ ‎27．（10分）（2020•常州）如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为H，且交⊙I于P、Q两点（Q在P、H之间）．我们把点P称为⊙I关于直线a的“远点“，把PQ•PH的值称为⊙I关于直线a的“特征数”．‎ ‎（1）如图2，在平面直角坐标系xOy中，点E的坐标为（0，4）．半径为1的⊙O与两坐标轴交于点A、B、C、D．‎ ‎①过点E画垂直于y轴的直线m，则⊙O关于直线m的“远点”是点　D　（填“A”．“B”、“C”或“D”），⊙O关于直线m的“特征数”为　6　；‎ ‎②若直线n的函数表达式为y‎=‎‎3‎x+4．求⊙O关于直线n的“特征数”；‎ ‎（2）在平面直角坐标系xOy中，直线l经过点M（1，4），点F是坐标平面内一点，以F为圆心，‎2‎为半径作⊙F．若⊙F与直线1相离，点N（﹣1，0）是⊙F关于直线1的“远点”．且⊙F关于直线l的“特征数”是4‎5‎，求直线l的函数表达式．‎ ‎【解答】解：（1）①由题意，点D是⊙O关于直线m的“远点”，⊙O关于直线m的特征数＝DB•DE＝2×5＝20，‎ 故答案为D，20．‎ ‎②如图1﹣1中，过点O作OH⊥直线n于H，交⊙O于Q，P．‎ 第28页（共28页）‎ 设直线y‎=‎‎3‎x+4交x轴于F（‎-‎‎4‎‎3‎‎3‎，0），交y轴于E（0，4），‎ ‎∴OE＝4，OF‎=‎‎4‎‎3‎‎3‎ ‎∴tan∠FEO‎=OFOE=‎‎3‎‎3‎，‎ ‎∴∠FEO＝30°，‎ ‎∴OH‎=‎‎1‎‎2‎OE＝2，‎ ‎∴PH＝OH+OP＝3，‎ ‎∴⊙O关于直线n的“特征数”＝PQ•PH＝2×3＝6．‎ ‎（2）如图2﹣1中，设直线l的解析式为y＝kx+b．‎ 当k＞0时，过点F作FH⊥直线l于H，交⊙F于E，N．‎ 由题意，EN＝2‎2‎，EN•NH＝4‎5‎，‎ ‎∴NH‎=‎‎10‎，‎ ‎∵N（﹣1，0），M（1，4），‎ ‎∴MN‎=‎2‎‎2‎‎+‎‎4‎‎2‎=‎2‎5‎，‎ 第28页（共28页）‎ ‎∴HM‎=MN‎2‎-NH‎2‎=‎20-10‎=‎‎10‎，‎ ‎∴△MNH是等腰直角三角形，‎ ‎∵MN的中点K（0，2），‎ ‎∴KN＝HK＝KM‎=‎‎5‎，‎ ‎∴H（﹣2，3），‎ 把H（﹣2，3），M（1，4）代入y＝kx+b，则有k+b=4‎‎-2k+b=3‎，‎ 解得k=‎‎1‎‎3‎b=‎‎11‎‎3‎，‎ ‎∴直线l的解析式为y‎=‎‎1‎‎3‎x‎+‎‎11‎‎3‎，‎ 当k＜0时，同法可知直线i经过H′（2，1），可得直线l的解析式为y＝﹣3x+7．‎ 综上所述，满足条件的直线l的解析式为y‎=‎‎1‎‎3‎x‎+‎‎11‎‎3‎或y＝﹣3x+7．‎ ‎28．（10分）（2020•常州）如图，二次函数y＝x2+bx+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，抛物线过点C（1，0），且顶点为D，连接AC、BC、BD、CD．‎ ‎（1）填空：b＝　﹣4　；‎ ‎（2）点P是抛物线上一点，点P的横坐标大于1，直线PC交直线BD于点Q．若∠CQD＝∠ACB，求点P的坐标；‎ ‎（3）点E在直线AC上，点E关于直线BD对称的点为F，点F关于直线BC对称的点为G，连接AG．当点F在x轴上时，直接写出AG的长．‎ ‎【解答】解：（1）∵抛物线y＝x2+bx+3的图象过点C（1，0），‎ ‎∴0＝1+b+3，‎ 第28页（共28页）‎ ‎∴b＝﹣4，‎ 故答案为：﹣4；‎ ‎（2）∵b＝4，‎ ‎∴抛物线解析式为y＝x2﹣4x+3‎ ‎∵抛物线y＝x2﹣4x+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，‎ ‎∴点A（0，3），3＝x2﹣4x，‎ ‎∴x1＝0（舍去），x2＝4，‎ ‎∴点B（4，3），‎ ‎∵y＝x2﹣4x+3＝（x﹣2）2﹣1，‎ ‎∴顶点D坐标（2，﹣1），‎ 如图1，当点Q在点D上方时，过点C作CE⊥AB于E，设BD与x轴交于点F，‎ ‎∵点A（0，3），点B（4，3），点C（1，0），CE⊥AB，‎ ‎∴点E（1，3），CE＝BE＝3，AE＝1，‎ ‎∴∠EBC＝∠ECB＝45°，tan∠ACE‎=AEEC=‎‎1‎‎3‎，‎ ‎∴∠BCF＝45°，‎ ‎∵点B（4，3），点C（1，0），点D（2，﹣1），‎ ‎∴BC‎=‎9+9‎=‎3‎2‎，CD‎=‎1+1‎=‎‎2‎，BD‎=‎(4-2)‎2‎+(3+1‎‎)‎‎2‎=‎2‎5‎，‎ ‎∵BC2+CD2＝20＝BD2，‎ ‎∴∠BCD＝90°，‎ ‎∴tan∠DBC‎=CDBC=‎2‎‎3‎‎2‎=‎1‎‎3‎=‎tan∠ACE，‎ ‎∴∠ACE＝∠DBC，‎ ‎∴∠ACE+∠ECB＝∠DBC+∠BCF，‎ 第28页（共28页）‎ ‎∴∠ACB＝∠CFD，‎ 又∵∠CQD＝∠ACB，‎ ‎∴点F与点Q重合，‎ ‎∴点P是直线CF与抛物线的交点，‎ ‎∴0＝x2﹣4x+3，‎ ‎∴x1＝1，x2＝3，‎ ‎∴点P（3，0）；‎ 当点Q在点D下方上，过点C作CH⊥DB于H，在线段BH的延长线上截取HF＝QH，连接CQ交抛物线于点P，‎ ‎∵CH⊥DB，HF＝QH，‎ ‎∴CF＝CQ，‎ ‎∴∠CFD＝∠CQD，‎ ‎∴∠CQD＝∠ACB，‎ ‎∵CH⊥BD，‎ ‎∵点B（4，3），点D（2，﹣1），‎ ‎∴直线BD解析式为：y＝2x﹣5，‎ ‎∴点F（‎5‎‎2‎，0），‎ ‎∴直线CH解析式为：y‎=-‎‎1‎‎2‎x‎+‎‎1‎‎2‎，‎ ‎∴y=-‎1‎‎2‎x+‎‎1‎‎2‎y=2x-5‎，‎ 第28页（共28页）‎ 解得x=‎‎11‎‎5‎y=-‎‎3‎‎5‎，‎ ‎∴点H坐标为（‎11‎‎5‎，‎-‎‎3‎‎5‎），‎ ‎∵FH＝QH，‎ ‎∴点Q（‎19‎‎10‎，‎-‎‎6‎‎5‎），‎ ‎∴直线CQ解析式为：y‎=-‎‎4‎‎3‎x‎+‎‎4‎‎3‎，‎ 联立方程组y=-‎4‎‎3‎x+‎‎4‎‎3‎y=x‎2‎-4x+3‎，‎ 解得：x‎1‎‎=1‎y‎1‎‎=0‎或x‎2‎=‎‎5‎‎3‎y‎2‎=-‎‎8‎‎9‎，‎ ‎∴点P（‎5‎‎3‎，‎-‎‎8‎‎9‎）；‎ 综上所述：点P的坐标为（3，0）或（‎5‎‎3‎，‎-‎‎8‎‎9‎）；‎ ‎（3）如图，设直线AC与BD的交点为N，作CH⊥BD于H，过点N作MN⊥x轴，过点E作EM⊥MN，连接CG，GF，‎ ‎∵点A（0，3），点C（1，0），‎ ‎∴直线AC解析式为：y＝﹣3x+3，‎ ‎∴y=-3x+3‎y=2x-5‎，‎ 第28页（共28页）‎ ‎∴x=‎‎8‎‎5‎y=-‎‎9‎‎5‎，‎ ‎∴点N坐标为（‎8‎‎5‎，‎-‎‎9‎‎5‎），‎ ‎∵点H坐标为（‎11‎‎5‎，‎-‎‎3‎‎5‎），‎ ‎∴CH2＝（‎11‎‎5‎‎-‎1）2+（‎3‎‎5‎）2‎=‎‎9‎‎5‎，HN2＝（‎11‎‎5‎‎-‎‎8‎‎5‎）2+（‎-‎3‎‎5‎+‎‎9‎‎5‎）2‎=‎‎9‎‎5‎，‎ ‎∴CH＝HN，‎ ‎∴∠CNH＝45°，‎ ‎∵点E关于直线BD对称的点为F，‎ ‎∴EN＝NF，∠ENB＝∠FNB＝45°，‎ ‎∴∠ENF＝90°，‎ ‎∴∠ENM+∠FNM＝90°，‎ 又∵∠ENM+∠MEN＝90°，‎ ‎∴∠MEN＝∠FNM，‎ ‎∴△EMN≌△NKF（AAS）‎ ‎∴EM＝NK‎=‎‎9‎‎5‎，MN＝KF，‎ ‎∴点E的横坐标为‎-‎‎1‎‎5‎，‎ ‎∴点E（‎-‎‎1‎‎5‎，‎18‎‎5‎），‎ ‎∴MN‎=‎27‎‎5‎=‎KF，‎ ‎∴CF‎=‎8‎‎5‎+‎27‎‎5‎-‎1＝6，‎ ‎∵点F关于直线BC对称的点为G，‎ ‎∴FC＝CG＝6，∠BCF＝∠GCB＝45°，‎ ‎∴∠GCF＝90°，‎ ‎∴点G（1，6），‎ ‎∴AG‎=‎1‎2‎+(6-3)‎‎2‎=‎‎10‎．‎ 第28页（共28页）‎