中考数学模压轴题精选doc

中考数学模压轴题精选doc

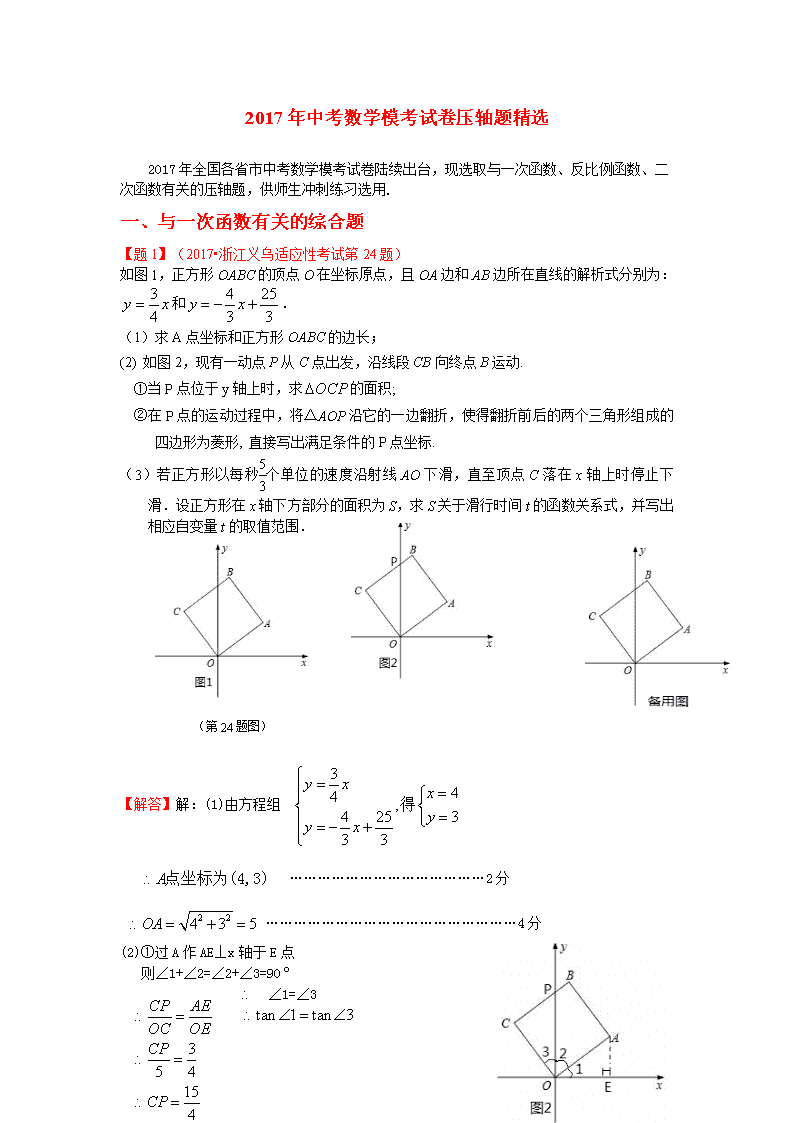
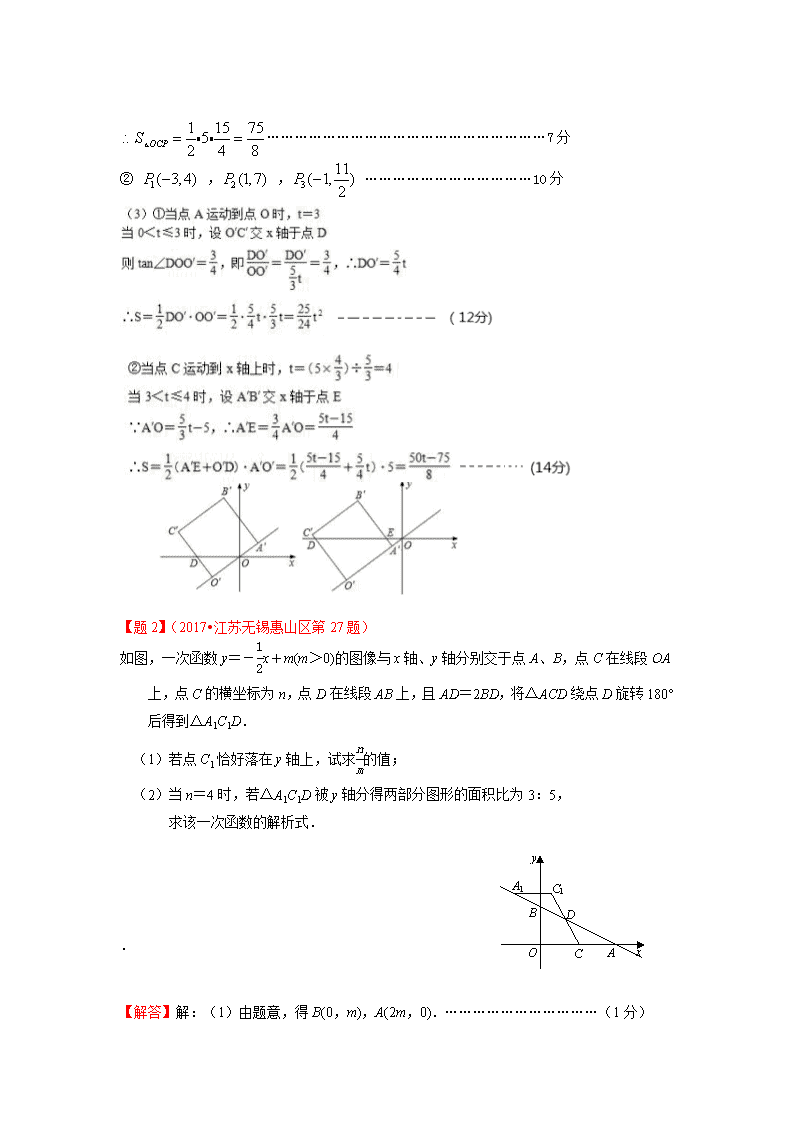
‎2017年中考数学模考试卷压轴题精选 ‎2017年全国各省市中考数学模考试卷陆续出台，现选取与一次函数、反比例函数、二次函数有关的压轴题，供师生冲刺练习选用.‎ 一、与一次函数有关的综合题 ‎【题1】（2017•浙江义乌适应性考试第24题）‎ 如图1，正方形OABC的顶点O在坐标原点，且OA边和AB边所在直线的解析式分别为：和．‎ ‎（1）求A点坐标和正方形OABC的边长；‎ ‎(2) 如图2，现有一动点P从C点出发，沿线段CB向终点B运动.‎ ‎①当P点位于y轴上时，求的面积;‎ ‎②在P点的运动过程中，将△AOP沿它的一边翻折，使得翻折前后的两个三角形组成的四边形为菱形, 直接写出满足条件的P点坐标.‎ ‎（3）若正方形以每秒个单位的速度沿射线AO下滑，直至顶点C落在x轴上时停止下滑．设正方形在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围．‎ ‎（第24题图）‎ ‎【解答】解：(1)由方程组 ‎ ‎ ……………………………………2分 ‎ ………………………………………………4分 ‎(2)①过A作AE⊥x轴于E点 则∠1+∠2=∠2+∠3=90 ‎ ‎ ∠1=∠3‎ ‎ ‎ ‎ ……………………………………………………7分 ‎② ， ， ………………………………10分 ‎【题2】（2017•江苏无锡惠山区第27题）‎ 如图，一次函数y＝－x＋m(m＞0)的图像与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD＝2BD，将△ACD绕点D旋转180°后得到△A‎1C1D． 2-1-c-n-j-y ‎（1）若点C1恰好落在y轴上，试求的值；‎ ‎（2）当n＝4时，若△A‎1C1D被y轴分得两部分图形的面积比为3：5，‎ 求该一次函数的解析式．‎ O A B C D C1‎ A1‎ x y ‎． ‎ ‎ ‎ ‎ ‎ ‎【解答】解：（1）由题意，得B(0，m)，A(‎2m，0)．……………………………（1分）‎ 如图，过点D作x轴的垂线，交x轴于点E，交直线A‎1C1于点F，‎ 易知：DE＝m，D(m，m) ，C1(m－n，m)．………………（3分）‎ ‎∴m－n＝0，∴＝；……………………………………………（4分）‎ ‎（2）由（1）得，当m＞3时，点C1在y轴右侧；当2＜m＜3时，点C1在y轴左侧．‎ ‎① 当m＞3时，设A‎1C1与y轴交于点P，连接C1B，‎ 由△A‎1C1D被y轴分得两部分图形的面积比为3：5，∴S△BA1P：S△BC1P＝3：1，‎ ‎∴A1P：C1P＝3，∴m＝3(m－4)，∴m＝．……………………（6分）‎ ‎∴y＝－x＋．………………………………………………………（7分）‎ ‎② 当2＜m＜3时，同理可得：y＝－x＋．……（10分）（参照①给分）‎ O A B C D C1‎ A1‎ x y E F P 综上所述，y＝－x＋或y＝－x＋．‎ 二、与轴对称和等腰三角形性质有关的综合题 ‎【题3】（2017•山东济南市中区第29题）‎ 如图，二次函数y=x2+bx﹣的图象与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．‎ ‎（1）请直接写出点D的坐标：　 　；‎ ‎（2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；‎ ‎（3）是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）将点A的坐标代入二次函数的解析式求得其解析式，然后求得点B的坐标即可求得正方形ABCD的边长，从而求得点D的纵坐标；‎ ‎（2）PA=t，OE=l，利用△DAP∽△POE得到比例式，从而得到有关两个变量的二次函数，求最值即可；‎ ‎（3）分点P位于y轴左侧和右侧两种情况讨论即可得到重叠部分的面积．‎ ‎【解答】解：（1）（﹣3，4）；‎ ‎（2）设PA=t，OE=l 由∠DAP=∠POE=∠DPE=90°得△DAP∽△POE ‎∴‎ ‎∴l=﹣+=﹣（t﹣）2+‎ ‎∴当t=时，l有最大值 即P为AO中点时，OE的最大值为；‎ ‎（3）存在．‎ ‎①点P点在y轴左侧时，DE交AB于点G，‎ P点的坐标为（﹣4，0），∴PA=OP﹣AO=4﹣3=1，‎ 由△PAD≌△EOP得OE=PA=1∵△ADG∽△OEG ‎∴AG：GO=AD：OE=4：1∴AG==‎ ‎∴重叠部分的面积==‎ ‎②当P点在y轴右侧时，P点的坐标为（4，0），‎ 此时重叠部分的面积为 ‎【题4】（2017•天津滨海新区第25题）‎ 已知抛物线的解析式为y=0.25x2-0.5x+0.25,P是抛物线上的一个动点，R(1,1)是抛物线对称轴上的一点.‎ ‎（Ⅰ）求抛物线的顶点及与y轴交点的坐标；‎ ‎（Ⅱ）1是过点(0,-1)且平行于x轴的直线,l与抛物线的对称轴的交点为N,PM=MN,垂足为点M，连接PR,RM.‎ ‎（ⅰ）当△RPM是等边三角形时，求P点的坐标；‎ ‎（ⅱ）求证：PR=PM.‎ ‎ ‎ 三、与相似三角形性质有关的综合题 ‎【题5】（2017•湖北武汉江岸区第24题）‎ 已知抛物线y=x2，B（2，m），点A在x轴负半轴上，AB交抛物线于点C ‎（1）若A（﹣2，0），求C点坐标；‎ ‎（2）若A为动点，BF⊥x轴于F，交直线CO于D点，求AF•（BF﹣FD）；‎ ‎（3）在（2）的条件下，若A点在x正半轴上，其他条件不变，问的值是否变化，试说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）可先求得B点坐标，利用待定系数法可求得直线AB的解析式，联立直线和抛物线解析式可求得C点坐标；‎ ‎（2）可设C（t，t2），过C作CH⊥x轴于点H，作CN⊥BF于点N，则可得△OCH∽△ODF和△BCN∽△ABF，利用相似三角形的性质可用t表示出AF、DF，代入可求得答案；‎ ‎（3）用t可表示出直线OC和AB的解析式，可表示出A、D的坐标，则可分别表示出△AOB 和△DAF的面积，可求得答案．‎ ‎【解答】解：‎ ‎（1）∵点B在抛物线y=x2上，‎ ‎∴m=22=4，‎ ‎∴B（2，4），‎ 设直线AB解析式为y=kx+b，‎ ‎∴，解得，‎ ‎∴直线AB解析式为y=x+2，‎ 联立直线AB与抛物线解析式可得，解得或，‎ ‎∴C（﹣1，1）；‎ ‎（2）过点C作CH⊥x轴于H，作CN⊥BF于N，如图1，‎ 设C（t，t2），则CH=t2，HO=﹣m，OF=2，BF=4，BN=4﹣t2，CN=2﹣t，‎ ‎∵CH∥BD，‎ ‎∴△OCH∽△ODF，‎ ‎∴=，即=，‎ ‎∴DF=﹣2t，‎ 同理△BCN∽△BAF，‎ ‎∴=，即=，‎ ‎∴AF=，‎ ‎∴AF•（BF﹣FD）=×（4+2t）=8；‎ ‎（3）不变化，理由如下：‎ 设直线BC的解析式为y=k′x+b′，‎ ‎∴，解得，‎ ‎∴直线BC的解析式为y=（t+2）x﹣2t，当y=0时，x=，‎ ‎∴OA=，‎ ‎∴S△OAB=OA•BF=××4=，‎ 设直线OC的解析式为y=sx，‎ ‎∴t2=ts，解得s=t，‎ ‎∴直线OC的解析式为y=tx，令x=2可得y=2t，‎ ‎∴D（2，2t），‎ ‎∴AF=OF﹣OA=2﹣，‎ ‎∴S△ADF=AF•DF=×（2﹣）×2t=，‎ ‎∴=1，‎ 即的值是不变化的．‎ ‎【点评】本题为二次函数的综合应用，涉及待定系数法、函数图象的交点、相似三角形的判定和性质、三角形的面积及方程思想等知识．在（1）中求得直线AB的解析式是解题的关键，在（2）中分别用C点的坐标表示出AF、BF和FD的长是解题的关键，在（3）中用C点的坐标分别表示出两三角形的面积是解题的关键．本题考查知识点较多，综合性较强，难度适中．‎ ‎【题6】（2017•江苏徐州第28题）‎ 二次函数y=ax2+bx+4的图象与x轴交于两点A、B，与y轴交于点C，且A（﹣1，0）、B（4，0）‎ ‎（1）求此二次函数的表达式 ‎（2）如图1，抛物线的对称轴m与x轴交于点E，CD⊥m，垂足为D，点F（﹣，0），动点N在线段DE上运动，连接CF、CN、FN，若以点C、D、N为顶点的三角形与△FEN 相似，求点N的坐标 ‎（3）如图2，点M在抛物线上，且点M的横坐标是1，点P为抛物线上一动点，若∠PMA=45°，求点P的坐标．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）先求得点C的坐标，设抛物线的解析式为y=a（x+1）（x﹣4），将点C的坐标代入求得a的值，从而得到抛物线的解析式；‎ ‎（2）先求得抛物线的对称轴，然后求得CD，EF的长，设点N的坐标为（0，a）则ND=4﹣a，NE=a，然后依据相似三角形的性质列出关于a的方程，然后可求得a的值；‎ ‎（3）过点A作AD∥y轴，过点M作DM∥x轴，交点为D，过点A作AE⊥AM，取AE=AM，作EF⊥x轴，垂足为F，连结EM交抛物线与点P．则△AME为等腰直角三角形，然后再求得点M的坐标，从而可得到MD=2，AD=6，然后证明∴△ADM≌△AFE，于是可得到点E的坐标，然后求得EM的解析式为y=﹣2x+8，最后求得直线EM与抛物线的交点坐标即可．‎ ‎【解答】解：（1）当x=0时，y=4，‎ ‎∴C（0，4）．‎ 设抛物线的解析式为y=a（x+1）（x﹣4），将点C的坐标代入得：﹣4a=4，解得a=﹣1，‎ ‎∴抛物线的解析式为y=﹣x2+3x+4．‎ ‎（2）x=﹣=．‎ ‎∴CD=，EF=．‎ 设点N的坐标为（0，a）则ND=4﹣a，NE=a．‎ 当△CDN∽△FEN时，，即，解得a=，‎ ‎∴点N的坐标为（0，）．‎ 当△CDN∽△NEF时，，即，解得：a=2．‎ ‎∴点N的坐标为（0，2）．‎ 综上所述，点N的坐标为（0，）或（0，2）．‎ ‎（3）如图所示：过点A作AD∥y轴，过点M作DM∥x轴，交点为D，过点A作AE⊥AM，取AE=AM，作EF⊥x轴，垂足为F，连结EM交抛物线与点P．‎ ‎∵AM=AE，∠MAE=90°，‎ ‎∴∠AMP=45°．‎ 将x=1代入抛物线的解析式得：y=6，‎ ‎∴点M的坐标为（1，6）．‎ ‎∴MD=2，AD=6．‎ ‎∵∠DAM+∠MAF=90°，∠MAF+∠FAE=90°，‎ ‎∴∠DAM=∠FAE．‎ 在△ADM和△AFE中，，‎ ‎∴△ADM≌△AFE．‎ ‎∴EF=DM=2，AF=AD=6．‎ ‎∴E（5，﹣2）．‎ 设EM的解析式为y=kx+b．‎ 将点M和点E的坐标代入得：，解得k=﹣2，b=8，‎ ‎∴直线EM的解析式为y=﹣2x+8．‎ 将y=﹣2x+8与y=﹣x2+3x+4联立，解得：x=1或x=4．‎ 将x=4代入y=﹣2x+8得：y=0．‎ ‎∴点P的坐标为（4，0）．‎ ‎【题7】（2017•浙江宁波第26题）‎ 已知：如图一，抛物线y=ax2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x﹣2经过A、C两点，且AB=2．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s=，当t为何值时，s有最小值，并求出最小值．‎ ‎（3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）首先根据直线AC的解析式确定点A、C的坐标，已知AB的长，进一步能得到点B的坐标；然后由待定系数法确定抛物线的解析式．‎ ‎（2）根据所给的s表达式，要解答该题就必须知道ED、OP的长；BP、CE长易知，那么由OP=OB﹣BP求得OP长，由∠CED的三角函数值可得到ED的长，再代入s的表达式中可得到关于s、t的函数关系式，结合函数的性质即可得到s的最小值．‎ ‎（3）首先求出BP、BD的长，若以P、B、D为顶点的三角形与△ABC相似，已知的条件是公共角∠OBC，那么必须满足的条件是夹公共角的两组对应边成比例，分两种情况讨论即可．‎ ‎【解答】解：（1）由直线：y=x﹣2知：A（2，0）、C（0，﹣2）；‎ ‎∵AB=2，∴OB=OA+AB=4，即 B（4，0）．‎ 设抛物线的解析式为：y=a（x﹣2）（x﹣4），代入C（0，﹣2），得：‎ a（0﹣2）（0﹣4）=﹣2，解得 a=﹣‎ ‎∴抛物线的解析式：y=﹣（x﹣2）（x﹣4）=﹣x2+x﹣2．‎ ‎（2）在Rt△OBC中，OB=4，OC=2，则 tan∠OCB=2；‎ ‎∵CE=t，∴DE=2t；‎ 而 OP=OB﹣BP=4﹣2t；‎ ‎∴s===（0＜t＜2），‎ ‎∴当t=1时，s有最小值，且最小值为 1．‎ ‎（3）在Rt△OBC中，OB=4，OC=2，则 BC=2；‎ 在Rt△CED中，CE=t，ED=2t，则 CD=t；‎ ‎∴BD=BC﹣CD=2﹣t；‎ 以P、B、D为顶点的三角形与△ABC相似，已知∠OBC=∠PBD，则有两种情况：‎ ‎①=⇒=，解得 t=；‎ ‎②=⇒=，解得 t=；‎ 综上，当t=或时，以P、B、D为顶点的三角形与△ABC相似．‎ 四、与图形的变换有关的综合题 ‎【题8】（2017•海南第24题）‎ 如图1，二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点，与y轴交于点C．若tan∠ABC=3，一元二次方程ax2+bx+c=0的两根为﹣8、2．‎ ‎（1）求二次函数的解析式；‎ ‎（2）直线l绕点A以AB为起始位置顺时针旋转到AC位置停止，l与线段BC交于点D，P是AD的中点．‎ ‎①求点P的运动路程；‎ ‎②如图2，过点D作DE垂直x轴于点E，作DF⊥AC所在直线于点F，连结PE、PF，在l运动过程中，∠EPF的大小是否改变？请说明理由；‎ ‎（3）在（2）的条件下，连结EF，求△PEF周长的最小值．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）利用tan∠ABC=3，得出C点坐标，再利用待定系数法求出二次函数解析式；‎ ‎（2）①当l在AB位置时，P即为AB的中点H，当l运动到AC位置时，P即为AC中点K，则P的运动路程为△ABC的中位线HK，再利用勾股定理得出答案；‎ ‎②首先利用等腰三角形的性质得出∠PAE=∠PEA=∠EPD，同理可得：∠PAF=∠PFA=∠DPF，进而求出∠EPF=∠EPD+∠FPD=2（∠PAE+∠PAF），即可得出答案；‎ ‎（3）首先得出C△PEF=AD+EF，进而得出EG=PE，EF=PE=AD，利用C△PEF=AD+EF=（1+）AD=AD，得出最小值即可．‎ ‎【解答】解：（1）∵函数y=ax2+bx+c与x轴交于A、B两点，且一元二次方程ax2+bx+c=0两根为：﹣8，2，‎ ‎∴A（﹣8，0）、B（2，0），即OB=2，‎ 又∵tan∠ABC=3，∴OC=6，即C（0，﹣6），‎ 将A（﹣8，0）、B（2，0）代入y=ax2+bx﹣6中，得：‎ ‎，‎ 解得：，‎ ‎∴二次函数的解析式为：y=x2+x﹣6；‎ ‎（2）①如图1，当l在AB位置时，P即为AB的中点H，‎ 当l运动到AC位置时，P即为AC中点K，‎ ‎∴P的运动路程为△ABC的中位线HK，‎ ‎∴HK=BC，‎ 在Rt△BOC中，OB=2，OC=6，‎ ‎∴BC=2，∴HK=，‎ 即P的运动路程为：；‎ ‎②∠EPF的大小不会改变，‎ 理由如下：如图2，∵DE⊥AB，‎ ‎∴在Rt△AED中，P为斜边AD的中点，‎ ‎∴PE=AD=PA，‎ ‎∴∠PAE=∠PEA=∠EPD，‎ 同理可得：∠PAF=∠PFA=∠DPF，‎ ‎∴∠EPF=∠EPD+∠FPD=2（∠PAE+∠PAF），‎ 即∠EPF=2∠EAF，‎ 又∵∠EAF大小不变，‎ ‎∴∠EPF的大小不会改变；‎ ‎（3）设△PEF的周长为C，则C△PEF=PE+PF+EF，‎ ‎∵PE=AD，PF=AD，‎ ‎∴C△PEF=AD+EF，‎ 在等腰三角形PEF中，如图2，过点P作PG⊥EF于点G，‎ ‎∴∠EPG=∠EPF=∠BAC，‎ ‎∵tan∠BAC==，‎ ‎∴tan∠EPG==，‎ ‎∴EG=PE，EF=PE=AD，‎ ‎∴C△PEF=AD+EF=（1+）AD=AD，‎ 又当AD⊥BC时，AD最小，此时C△PEF最小，‎ 又S△ABC=30，‎ ‎∴BC×AD=30，‎ ‎∴AD=3，‎ ‎∴C△PEF最小值为： AD=．‎ ‎ ‎ ‎　‎ ‎【题9】（2017•重庆第25题）‎ 如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17，抛物线y=x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K．‎ ‎（1）将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处．‎ ‎①点B的坐标为（ 、 ）,BK的长是 ,CK的长是 ；‎ ‎②求点F的坐标；‎ ‎③请直接写出抛物线的函数表达式；‎ ‎（2）将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点（不与点H重合）,连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON，点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1•S2（即S1与S2的积）的值是否发生变化?若变化，请直接写出变化范围；若不变，请直接写出这个值．‎ ‎【解答】解：（1）如图1中，①∵抛物线y=x2﹣3x+m的对称轴x=﹣=10，∴点B坐标（10，0），‎ ‎∵四边形OBKC是矩形，∴CK=OB=10，KB=OC=8，故答案分别为10，0，8，10．‎ ‎②在RT△FBK中，∵∠FKB=90°，BF=OB=10，BK=OC=8，∴FK==6，‎ ‎∴CF=CK﹣FK=4，∴点F坐标（4，8）．‎ ‎③设OA=AF=x，在RT△ACF中，∵AC2+CF2=AF2，∴（8﹣x）2+42=x2，∴x=5，‎ ‎∴点A坐标（0，5），代入抛物线y=x2﹣3x+m得m=5，∴抛物线为y=x2﹣3x+5．‎ ‎（2）不变．S1•S2=189．理由：如图2中，在RT△EDG中，∵GE=EO=17，ED=8，‎ ‎∴DG===15，∴CG=CD﹣DG=2，∴OG===2，‎ ‎∵CP⊥OM，MH⊥OG，∴∠NPN=∠NHG=90°，‎ ‎∵∠HNG+∠HGN=90°，∠PNM+∠PMN=90°，∠HNG=∠PNM，∴∠HGN=∠NMP，‎ ‎∵∠NMP=∠HMG，∠GHN=∠GHM，∴△GHN∽△MHG，∴=，‎ ‎∴GH2=HN•HM，∵GH=OH=，∴HN•HM=17，‎ ‎∵S1•S2=•OG•HN••OG•HM=（•2）2•17=289．‎ ‎【题10】（2017•武汉第24题）‎ 已知O点为坐标原点，抛物线y1=ax2+bx+c(a≠0)与y轴交于点C，且O，C两点间的距离为3.‎ ‎ (1)求点C的坐标；‎ ‎(2)抛物线y1=ax2+bx+c(a≠0)与x轴交于点A(x1,0),B(x2,0),x1∙x2<0,|x1|+|x2|=4.点A，C在直线y2=-3x+t上.‎ ‎ ①求该抛物线的顶点坐标；‎ ‎ ②将抛物线y1=ax2+bx+c(a≠0)向左平移n(n>0)个单位，记平移后y随x的增大而增大的部分为P，直线y2=-3x+t向下平移n个单位，当平移后的直线与P有公共点，求2n2-5n的最小值.‎ ‎【解答】解：（1）令x=0，则y=c， 故C（0，c），  ∵OC的距离为3， ∴|c|=3，即c=±3， ∴C（0，3）或（0，-3）；  （2）∵x1x2＜0， ∴x1，x2异号，  ①若C（0，3），即c=3， 把C（0，3）代入y2=-3x+t，则0+t=3，即t=3，∴y2=-3x+3，  把A（x1，0）代入y2=-3x+3，则-3x1+3=0，即x1=1， ∴A（1，0），  ∵x1，x2异号，x1=1＞0，∴x2＜0， ∵|x1|+|x2|=4， ∴1-x2=4，  解得：x2=-3，则B（-3，0）， 代入y1=aa-b-3＝09a+3b-3＝0，  解得：a＝1b＝-2， ∴y1=x2-2x-3=（x-1）2-4， 则当x≥1时，y随x增大而增大，  综上所述，若c=3，当y随x增大而增大时，x≤-1；  若c=-3，当y随x增大而增大时，x≥1；  （3）①若c=3，则y1=-x2-2x+3=-（x+1）2+4，y2=-3x+3，  y1向左平移n个单位后，则解析式为：y3=-（x+1+n）2+4，  则当x≤-1-n时，y随x增大而增大，  y2向下平移n个单位后，则解析式为：y4=-3x+3-n，  要使平移后直线与P有公共点，则当x=-1-n，y3≥y4，  即-（-1-n+1+n）2+4ax2+bx+3得，a+b+3＝09a-3b+3＝0，  解得：a＝-1b＝-2， ∴y1=-x2-2x+3=-（x+1）2+4， 则当x≤-1时，y随x增大而增大．  ②若C（0，-3），即c=-3， 把C（0，-3）代入y2=-3x+t，则0+t=-3，即t=-3，  ∴y2=-3x-3， 把A（x1，0），代入y2=-3x-3， 则-3x1-3=0， 即x1=-1，  ∴A（-1，0）， ∵x1，x2异号，x1=-1＜0，∴x2＞0 ∵|x1|+|x2|=4，  ∴1+x2=4， 解得：x2=3，则B（3，0）， 代入y1=ax2+bx+3得，-1-n）+3-n，得：n≤-1，  ∵n＞0，∴n≤-1不符合条件，应舍去；  ②若c=-3，则y1=x2-2x-3=（x-1）2-4，y2=-3x-3，  y1向左平移n个单位后，则解析式为：y3=（x-1+n）2-4，  则当x≥1-n时，y随x增大而增大，  y2向下平移n个单位后，则解析式为：y4=-3x-3-n，  要使平移后直线与P有公共点，则当x=1-n，y3≤y4，  即（1-n-1+n）2-4≤-3（1-n）-3-n， 解得：n≥1， 综上所述：n≥1，  2n2-5n=2（n-54）2-25/8，  ∴当n=54时，2n2-5n的最小值为：-25/8．‎ 五、与特殊四边形及三角形面积有关的综合题 ‎【题11】（2017•吉林长春第24题）‎ 如图，在平面直角坐标系中，直线y=﹣x+4与x轴、y轴分别交于点A、B．抛物线y=﹣+n的顶点P在直线y=﹣x+4上，与y轴交于点C（点P、C不与点B重合），以BC为边作矩形BCDE，且CD=2，点P、D在y轴的同侧．‎ ‎（1）n=　﹣m+4　（用含m的代数式表示），点C的纵坐标是　﹣m2﹣m+4　（用含m的代数式表示）．‎ ‎（2）当点P在矩形BCDE的边DE上，且在第一象限时，求抛物线对应的函数表达式．‎ ‎（3）设矩形BCDE的周长为d（d＞0），求d与m之间的函数表达式．‎ ‎（4）直接写出矩形BCDE有两个顶点落在抛物线上时m的值．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）根据二次函数的解析式写出顶点P的坐标（m，n），又因为点p在直线y=﹣x+4上，将p点坐标代入可求出n，将二次函数化成一般式后得出点C的纵坐标，并将其化成含m的代数式；‎ ‎（2）当点P在矩形BCDE的边DE上，且在第一象限时，由CD=2可知，点P的横坐标为2，可求得纵坐标为2，则P（2，2），得出抛物线对应的函数表达式；‎ ‎（3）根据坐标表示出边BC的长，由矩形周长公式表示出d；‎ ‎（4）首先点B与C不能重合，因此点B不会在抛物线上，则分两类情况讨论：①点C、D在抛物线上时；②点C、E在抛物线上时；由（1）的结论计算出m的值．‎ ‎【解答】解：（1）y=﹣（x﹣m）2+n=﹣x2+mx﹣m2+n，‎ ‎∴P（m，n），‎ ‎∵点P在直线y=﹣x+4上，‎ ‎∴n=﹣m+4，‎ 当x=0时，y=﹣m2+n=﹣m2﹣m+4，‎ 即点C的纵坐标为：﹣m2﹣m+4，‎ 故答案为：﹣m+4，﹣m2﹣m+4；‎ ‎（2）∵四边形BCDE是矩形，‎ ‎∴DE∥y轴．‎ ‎∵CD=2，‎ ‎∴当x=2时，y=2．‎ ‎∴DE与AB的交点坐标为（2，2）． ‎ ‎∴当点P在矩形BCDE的边DE上时，抛物线的顶点P坐标为（2，2）．‎ ‎∴抛物线对应的函数表达式为． ‎ ‎（3）∵直线y=﹣x+4与y轴交于点B，‎ ‎∴点B的坐标是（0，4）．‎ 当点B与点C重合时，．‎ 解得m1=0，m2=﹣3．‎ i）当m＜﹣3或m＞0时，如图①、②，．． ‎ ii）当﹣3＜m＜0时，如图③，．． ‎ ‎（4）如图④⑤，点C、D在抛物线上时，由CD=2可知对称轴为：x=±1，即m=±1；‎ 如图⑥⑦，点C、E在抛物线上时，由B（0，4）和CD=2得：E（﹣2，4）‎ 则4=﹣（﹣2﹣m）2+（﹣m+4），解得：、． ‎ 综上所述：m=1、m=﹣1、、．‎ ‎【题12】（2017•苏州第27题）‎ 如图，已知抛物线(a为常数，且a＞0)与x轴从左至右 ‎ 依次交于A，B两点，与y轴交于点C，经过点B的直线与抛物线的另一交 ‎ 点为D，且点D的横坐标为﹣5．‎ ‎(1)求抛物线的函数表达式；‎ ‎(2)P为直线BD下方的抛物线上的一点，连接PD、PB, 求△PBD面积的最大值．[来源:学科网ZXXK]‎ ‎(3)设F为线段BD上一点(不含端点)，连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少？‎ D B O A y x C D B O A y x C ‎ 备用图 ‎【解答】 (1)抛物线令y＝0，解得x＝－2或x＝4，‎ ‎∴A(－2，0)，B(4，0)．‎ ‎∵直线经过点B(4，0)，∴，解得，‎ ‎∴直线BD解析式为：．------------------------------------1分2·1·c·n·j·y 当x＝－5时，y＝3，∴D(－5，3)．-------------------------------------2分 ‎∵点D(－5，)在抛物线上，‎ ‎∴，∴．‎ ‎∴抛物线的函数表达式为：．--------3分 ‎(2)设P(m, ) ‎ ‎∴‎ ‎-----------------5分．‎ ‎ ∴△BPD面积的最大值为．-------------------------------------------------6分．‎ ‎(3)作DK∥AB，AH⊥DK，AH交直线BD于点F，‎ ‎∵由(2)得，DN＝,BN＝9，容易得∠DBA＝30°，∴∠BDH＝30°，‎ ‎∴FG＝DF×sin30°＝，‎ ‎∴当且仅当AH⊥DK时，AF+FH最小，-----------------------8分 点M在整个运动中用时为：t＝，‎ ‎∵lBD：，∴Fx＝Ax＝－2，F(－2，)‎ ‎∴当F坐标为(－2，)时，用时最少．-----------------10分 六、与反比例函数有关的综合题 ‎【题13】（2017•上海黄浦区第24题）‎ 如图，点A在函数图像上，过点A作x轴和y轴的平行线分别交函数 图像于点B、C，直线BC与坐标轴的交点为D、E.‎ ‎（1）当点C的横坐标为1时，求点B的坐标；‎ ‎（2）试问：当点A在函数图像上运动时，△ABC的面积是否发生变化？若不变，请求出△ABC的面积；若变化，请说明理由；‎ ‎（3）试说明：当点A在函数图像上运动时，线段BD与CE的长始终相等.‎ E B C A D x y O ‎【解答】解：（1）由点C的横坐标为1，且AC平行于y轴，‎ 所以点A的横坐标也为1，且位于函数图像上，则.—————（2分）‎ 又AB平行于x轴，‎ 所以点B的纵坐标为4，且位于函数图像上，则.————（2分）‎ ‎（2）令，由题意可得：，. ———————（1分）‎ 于是△ABC的面积为：， ————（2分）‎ 所以△ABC的面积不变，为.———————————————————（1分）‎ ‎（3）分别延长AB、AC交坐标轴于点F、G. —————————————（1分）‎ ‎ 则，.‎ ‎ ∵DF∥AC，——————————————————————————（1分）‎ ‎ ∴，即.———————————（1分）‎ ‎ 同理，‎ ‎ 所以BD=CE. ——————————————————————————（1分）‎