2012年天津市中考数学试卷及答案

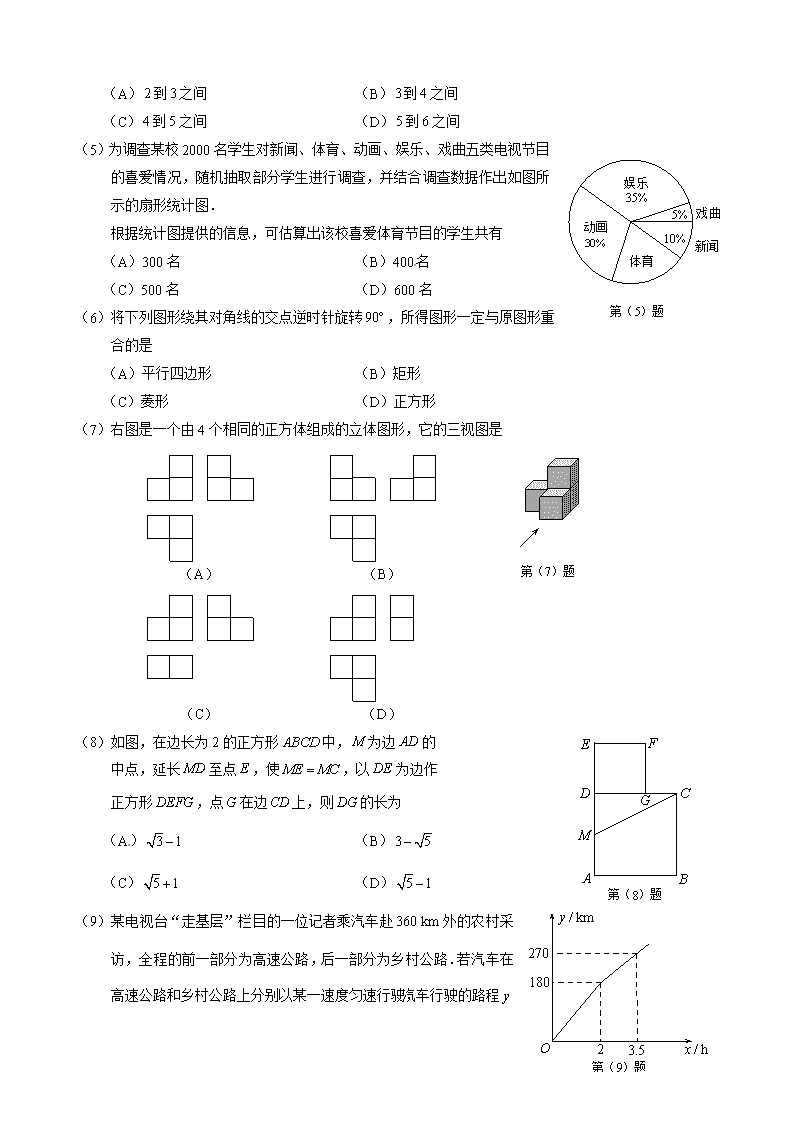
2012年天津市中考数学试卷及答案

机密★启用前 ‎2012年天津市初中毕业生学业考试试卷 数 学 本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。试卷满分120分。考试时间100分钟。‎ 答卷前，请你务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。考试结束后，将本试卷和“答题卡”一并交回。‎ 祝你考试顺利!‎ 第Ⅰ卷 注意事项：‎ ‎1．每题选出答案后，用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。‎ ‎ 2．本卷共10题，共30分。‎ 一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎（1）的值等于 ‎（A） （B）‎ ‎（C） （D）‎ ‎（2）下列标志中，可以看作是中心对称图形的是 ‎（A）‎ ‎ ‎（B）‎ ‎（C）‎ ‎‎（D）‎ ‎（3）据某域名统计机构公布的数据显示，截至2012年5月21日，我国“.NET”域名注册量约为560 000个，居全球第三位．将560 000用科学记数法表示应为 ‎（A） （B）‎ ‎（C） （D）‎ ‎（4）估计的值在 ‎（A）到之间 （B）到之间 ‎（C）到之间 （D）到之间 第（5）题 ‎（5）为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结合调查数据作出如图所示的扇形统计图．‎ 根据统计图提供的信息，可估算出该校喜爱体育节目的学生共有 ‎（A）300名 （B）400名 ‎ （C）500名 （D）600名 ‎（6）将下列图形绕其对角线的交点逆时针旋转，所得图形一定与原图形重合的是 ‎（A）平行四边形 （B）矩形 ‎（C）菱形 （D）正方形 ‎（7）右图是一个由4个相同的正方体组成的立体图形，它的三视图是 ‎（A）‎ ‎（B）‎ 第（7）题 ‎（D）‎ ‎（C）‎ 第（8）题 ‎（8）如图，在边长为2的正方形中，为边的 中点，延长至点，使，以为边作 正方形，点在边上，则的长为 ‎（A） （B）‎ ‎（C） （D）[来源:Z*xx*k.Com]‎ 第（9）题 ‎（9）某电视台“走基层”栏目的一位记者乘汽车赴km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程 ‎（单位：km）与时间（单位：h）之间的关系如图所示，则下列结论正确的是[来源:学科网]‎ ‎（A）汽车在高速公路上的行驶速度为km/h ‎（B）乡村公路总长为km ‎（C）汽车在乡村公路上的行驶速度为km/h ‎（D）该记者在出发后h到达采访地 ‎（10）若关于的一元二次方程有实数根且，有下列结论：‎ ‎①，； ②；‎ ‎③二次函数的图象与轴交点的坐标为和．‎ 其中，正确结论的个数是 ‎（A）0 （B）1‎ ‎（C）2 （D）3‎ 第Ⅱ卷 注意事项：‎ ‎1．用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。‎ ‎　　2．本卷共16题，共90分。‎ 二、填空题（本大题共8小题，每小题3分，共24分）‎ 得分 ‎（11） ．‎ 第（15）题 ‎（12）化简的结果是 ．‎ ‎（13）袋子中装有5个红球和3个黑球，这些球除了颜色外都相同．从袋子中随机地摸出1个球，则它是红球的概率是 ．‎ ‎（14）将正比例函数的图象向上平移，则平移后所得图象对应的函数解析式可以是 （写出一个即可）．‎ 第（17）题 ‎（15）如图，是的内接三角形，为的直径，点为上一点，若，则的大小为 （度）．‎ ‎（16）若一个正六边形的周长为24，则该正六边形的面积为 ．‎ ‎（17）如图，已知正方形的边长为1，以顶点、为圆心，1为半径的两弧交于点，以顶点、为圆心，1为半径的两弧交于点，则的长为 ．‎ ‎（18）“三等分任意角”是数学史上一个著名问题已知一个角设 ‎ （Ⅰ）当时，的大小为 （度）；‎ ‎ （Ⅱ）如图，将放置在每个小正方形的边长为cm的网格中，角的一边与水平方向的网格线平行，另一边经过格点，且cm．现要求只能使用带刻度的直尺，请你在图中作出，并简要说明作法（不要求证明） ．‎ 第（18）题 三、解答题（本大题共8小题，共66分．解答应写出文字说明、演算步骤或推理过程）‎ ‎（19）（本小题6分）[来源:学科网ZXXK]‎ 解不等式组 ‎（20）（本小题8分）‎ 已知反比例函数（为常数，）．‎ ‎（Ⅰ）其图象与正比例函数的图象的一个交点为，若点的纵坐标是，求的值；‎ ‎（Ⅱ）若在其图象的每一支上，随的增大而减小，求的取值范围；‎ ‎（Ⅲ）若其图象的一支位于第二象限，在这一支上任取两点、，当时，试比较与的大小．‎ ‎（21）（本小题8分）‎ 在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：‎ 人数 第（21）题 次数 ‎（Ⅰ）求这50个样本数据的平均数、众数和中位数；‎ ‎（Ⅱ）根据样本数据，估算该校1200名学生共参加了多少次活动．‎ ‎（22）（本小题8分）‎ 已知⊙中，为直径，、分别切⊙于点、．‎ ‎（Ⅰ）如图①，若，求的大小；‎ ‎（Ⅱ）如图②，过点作于点，交⊙于点，若，求的大小．‎ 图①‎ 图②‎ 第（22）题 ‎（23）（本小题8分）‎ 第（23）题 ‎（甲）‎ ‎（乙）‎ 如图，甲楼的高度为m，自甲楼楼顶处，测得乙楼顶端处的仰角为，测得乙楼底部处的俯角为，求乙楼的高度（结果精确到m，取）．‎ ‎（24）（本小题8分）‎ 温馨提示：‎ 若选用方式一，每月固定交费58元，当主动打出电话月累计时间不超过150分，不再额外交费；当超过150分，超过部分每分加收0.25元．‎ 某通讯公司推出了移动电话的两种计费方式（详情见下表）．‎ 月使用费/元 主叫限定时间/分 主叫超时费/（元/分）‎ 被叫 方式一 ‎58‎ ‎150[来源:学科网ZXXK]‎ ‎0.25‎ 免费 方式二 ‎88‎ ‎350‎ ‎0.19‎ 免费 设一个月内使用移动电话主叫的时间为分（为正整数），‎ 请根据表中提供的信息回答下列问题：‎ ‎（Ⅰ）用含有的式子填写下表：‎ 方式一计费/元 ‎58‎ ‎108‎ 方式二计费/元 ‎88‎ ‎88‎ ‎88‎ ‎（Ⅱ）当为何值时，两种计费方式的费用相等；‎ ‎（Ⅲ）当时，你认为选用哪种计费方式省钱（直接写出结果即可）．‎ ‎（25）（本小题10分）‎ 已知一个矩形纸片，将该纸片放置在平面直角坐标系中，点，点，点为边上的动点（点不与点、重合），经过点、折叠该纸片，得点和折痕．设．‎ ‎（Ⅰ）如图①，当时，求点的坐标；‎ 第（25）题 图①‎ 图②‎ ‎（Ⅱ）如图②，经过点再次折叠纸片，使点落在直线上，得点和折痕，若，试用含有的式子表示；‎ ‎（Ⅲ）在（Ⅱ）的条件下，当点恰好落在边上时，求点的坐标（直接写出结果即可）．‎ ‎（26）（本小题10分）‎ 已知抛物线（）的顶点为，点、、在该抛物线上．‎ ‎（Ⅰ）当，，时，①求顶点的坐标；②求的值；‎ ‎（Ⅱ）当恒成立时，求的最小值．‎ ‎ ‎ 机密★启用前 ‎2012年天津市初中毕业生学业考试 数学参考答案 一、选择题（本大题共10小题，每小题3分，共30分）‎ ‎（1）A （2）B （3）C （4）B （5） B[来源:学。科。网Z。X。X。K]‎ ‎（6）D （7）A （8）D （9）C （10）C 二、填空题（本大题共8小题，每小题3分，共24分）‎ ‎（11） （12） （13）‎ ‎（14）（答案不惟一，可以是形如，的一次函数）‎ ‎（15） （16） （17） ‎ ‎（18）（Ⅰ）；（Ⅱ）如图，让直尺有刻度一边过点，设该边与过点的竖直方向的网格线交于点，与过点的水平方向的网格线交于点；保持直尺有刻度的一边过点，调整点、的位置，使，画射线，此时即为所求的．‎ 三、解答题（本大题共8小题，共66分）‎ ‎（19）（本小题6分）[来源:学|科|网Z|X|X|K]‎ 解： ∵ ‎ 解不等式①，得．‎ 解不等式②，得．‎ ‎∴ 不等式组的解集为．‎ ‎（20）（本小题8分）‎ 解：（Ⅰ）由题意，设点的坐标为，‎ ‎∵ 点在正比例函数的图象上，‎ ‎∴ ，即 ．‎ ‎∴ 点的坐标为．‎ ‎∵ 点在反比例函数的图象上，‎ ‎∴ ，解得．‎ ‎（Ⅱ）∵ 在反比例函数图象的每一支上，随的增大而减小，‎ ‎∴ ，解得．[来源:学&科&网]‎ ‎（Ⅲ）∵ 反比例函数图象的一支位于第二象限，[来源:学#科#网]‎ ‎ ∴ 在该函数图象的每一支上，随的增大而增大．‎ ‎ ∵ 点与点在该函数的第二象限的图象上，且，‎ ‎∴ ．‎ ‎（21）（本小题8分）‎ 解：（Ⅰ）观察条形统计图，可知这组样本数据的平均数是 ‎，[来源:学_科_网Z_X_X_K]‎ ‎∴ 这组样本数据的平均数是3.3．‎ ‎∵ 在这组样本数据中，4出现了18次，出现的次数最多，‎ ‎∴ 这组数据的众数是4．‎ ‎∵ 将这组样本数据按从小到大的顺序排列，其中处在中间的两个数都是3，‎ 有，‎ ‎∴ 这组数据的中位数是3．‎ ‎（Ⅱ）∵ 这组样本数据的平均数是3.3，‎ ‎∴ 估计全校1200人参加活动次数的总体平均数是3.3，‎ ‎ 有 ．‎ ‎∴ 该校学生共参加活动约3960次．‎ ‎（22）（本小题8分）‎ 解：（Ⅰ）∵ 切⊙于点，有．‎ 又 ，‎ ‎∴ ．‎ ‎∵ 、分别切⊙于点、，‎ ‎∴ ，有．‎ ‎∴ ．‎ ‎（Ⅱ）如图，连接、．‎ ‎∵ ，又 ，‎ ‎∴ ．‎ 又 ，‎ ‎∴ 四边形是平行四边形．‎ ‎∵ ，‎ ‎∴ 四边形是菱形，有．[来源:Z。xx。k.Com]‎ 又为直径，，得，有．‎ ‎∴ 是等边三角形，有．‎ ‎∴ 在菱形中，．‎ ‎（23）（本小题8分）‎ 解： 如图，过点作于点，‎ 根据题意，，．‎ ‎∵ ，，‎ ‎∴ 四边形为矩形．‎ ‎∴ ．‎ 在中，，‎ ‎∴ ．‎ 在中，由，‎ 得 ．‎ ‎∴ ．‎ 答：乙楼的高度约为m．‎ ‎（24）（本小题8分）‎ 解：（Ⅰ）当时，方式一：；‎ 当时，方式一：；方式二：．‎ ‎（Ⅱ）∵ 当时，，‎ ‎∴ 当两种计费方式的费用相等时，的值在取得．‎ ‎∴ 列方程，解得．‎ 答：当主叫时间为分时，两种计费方式的费用相等．‎ ‎（Ⅲ）方式二．‎ ‎（25）（本小题10分）‎ 解：（Ⅰ）根据题意，，，‎ 在中，由，，得．‎ 根据勾股定理，，‎ 即 ，解得（舍去）．‎ ‎∴ 点的坐标为．‎ ‎（Ⅱ）∵ 、分别是由、折叠得到的，‎ 有≌，≌．‎ ‎∴ ，．‎ ‎∵ ，‎ ‎∴ ．‎ ‎∵ ，‎ ‎∴ ．‎ 又，‎ ‎∴ ∽，有．‎ 由题设，，，，则，．‎ ‎∴ ．‎ ‎∴ （）即为所求．‎ ‎（Ⅲ）点的坐标为或． ‎ ‎（26）（本小题10分）‎ 解：（Ⅰ）若，，，‎ 此时抛物线的解析式为．‎ ‎① ∵ ，‎ ‎∴ 抛物线的顶点坐标为；‎ ‎② ∵点、、在抛物线上，‎ ‎∴ ，，．‎ ‎∴ ．‎ ‎（Ⅱ）由，得．‎ 由题意，如图，过点作轴于点，则，．‎ 连接，过点作轴于点，则，．‎ 过点作，交抛物线于点，交轴于点，‎ 则．‎ 于是∽．‎ 有，即．‎ 过点作于点，‎ 易得．‎ 有 ，即 ．‎ ‎∵ 点、、、在抛物线上，‎ 得，，，，‎ ‎∴ ．‎ 化简，得，解得（舍去）．‎ ‎∵ 恒成立，根据题意，有，‎ 则，即．‎ ‎∴ 的最小值为．‎