中考模拟试卷数学试卷和答案

中考模拟试卷数学试卷和答案

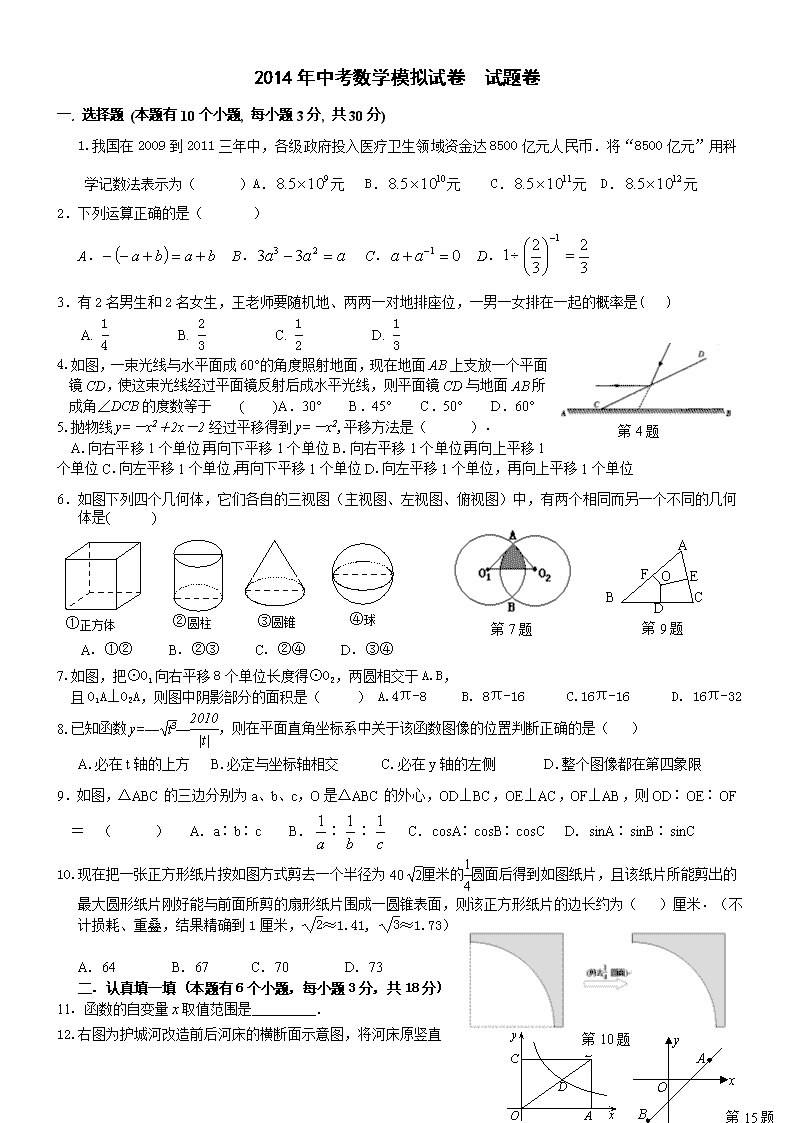
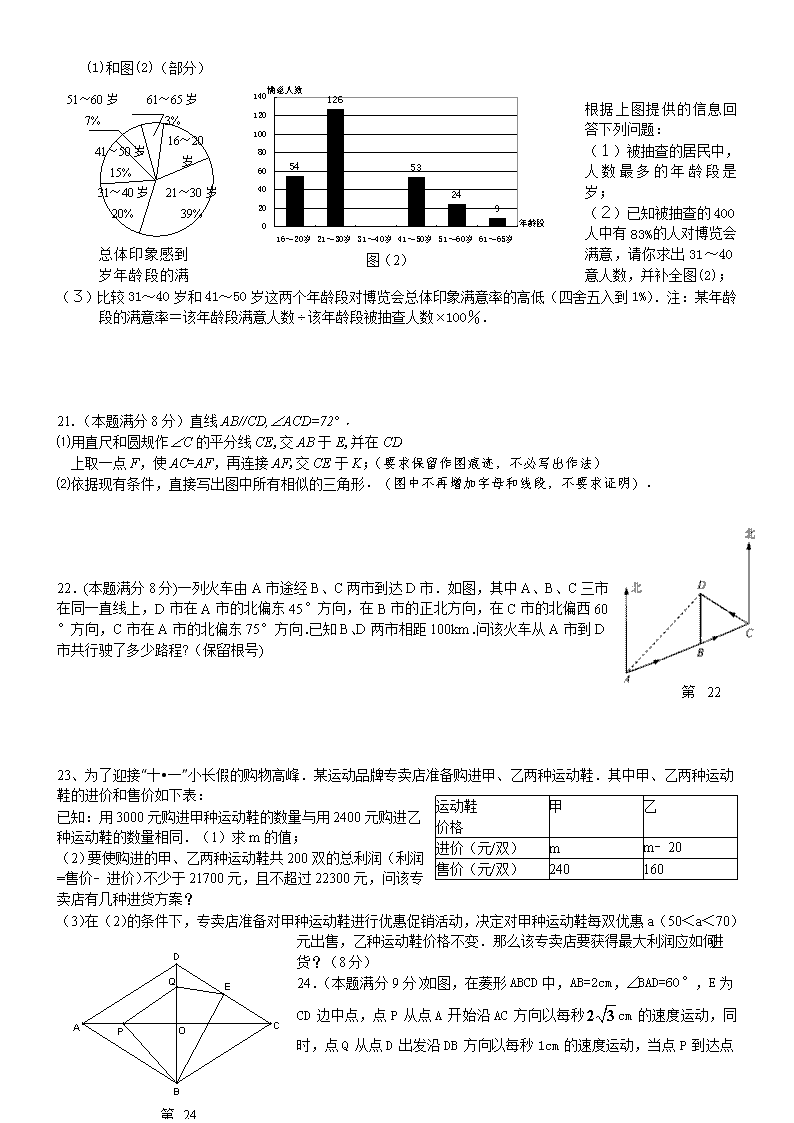
‎2014年中考数学模拟试卷 试题卷 一. 选择题 (本题有10个小题, 每小题3分, 共30分) ‎ ‎ 1.我国在2009到2011三年中，各级政府投入医疗卫生领域资金达8500亿元人民币．将“8500亿元”用科学记数法表示为（ ）A．元 B．元 C．元 D．元 ‎2．下列运算正确的是（ ）‎ A． B． C． D．‎ ‎3．有2名男生和2名女生，王老师要随机地、两两一对地排座位，一男一女排在一起的概率是( )‎ 第4题 A. B. C. D. ‎ ‎4.如图，一束光线与水平面成60°的角度照射地面，现在地面AB上支放一个平面镜CD，使这束光线经过平面镜反射后成水平光线，则平面镜CD与地面AB所成角∠DCB的度数等于 ( )A．30° B．45° C．50° D．60°‎ ‎5.抛物线y=－x2＋2x－2经过平移得到y=－x2,平移方法是（ ）﹒‎ A.向右平移1个单位，再向下平移1个单位B.向右平移1个单位，再向上平移1个单位C.向左平移1个单位，再向下平移1个单位D.向左平移1个单位，再向上平移1个单位 ‎6．如图下列四个几何体，它们各自的三视图（主视图、左视图、俯视图）中，有两个相同而另一个不同的几何体是( )‎ A B C O E F D 第9题 第7题 ‎①正方体 ‎②圆柱 ‎③圆锥 ‎④球 A. ①② B. ②③ C. ②④ D. ③④ ‎ ‎7.如图，把⊙O1向右平移8个单位长度得⊙O2，两圆相交于A.B，‎ 且O1A⊥O2A，则图中阴影部分的面积是（ ） A.4π-8 B. 8π-16 C.16π-16 D. 16π-32‎ ‎8.已知函数y=――，则在平面直角坐标系中关于该函数图像的位置判断正确的是（ ）‎ A.必在t轴的上方 B.必定与坐标轴相交 C.必在y轴的左侧 D.整个图像都在第四象限 ‎9．如图，△ABC的三边分别为a、b、c，O是△ABC的外心，OD⊥BC，OE⊥AC，OF⊥AB，则OD∶OE∶OF＝ （ ） A. a∶b∶c B. ∶∶ C. cosA∶cosB∶cosC D. sinA∶sinB∶sinC ‎ 第10题 ‎10.现在把一张正方形纸片按如图方式剪去一个半径为40厘米的圆面后得到如图纸片，且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面，则该正方形纸片的边长约为（ ）厘米﹒（不计损耗、重叠，结果精确到1厘米，≈1.41, ≈1.73）‎ ‎ ‎ A. 64 B. 67 C. 70 D. 73‎ 二. 认真填一填 (本题有6个小题, 每小题3分, 共18分)‎ ‎11. 函数的自变量取值范围是 ．‎ y x O A B 第15题 A B C D O x y 第13题 ‎12.右图为护城河改造前后河床的横断面示意图，将河床原竖直 迎水面BC改建为坡度1：0．5的迎水坡AB，已知AB=4米，‎ 则河床面的宽减少了 米．（即求AC的长） ‎ ‎13.已知矩形OABC的面积为，它的对角线OB与双曲线 相交于点D，且OB∶OD＝5∶3，则k＝__________．‎ ‎ ‎ ‎14.已知关于x的函数y＝（m－1）x2＋2x＋m图像与坐标轴 ‎…‎ ‎① ② ③ ④ ‎ 第16题 有且只有一个交点，则m＝ ‎ ‎15.如图，直线经过，两点，‎ 则不等式的解集为 ．‎ ‎16.如图，图①是一块边长为1，周长记为P1的正三角形纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的）后，得图③，④，…，记第n(n≥3) 块纸板的周长为Pn，则Pn-Pn-1= . ‎ 三.解答题：（计72分） ‎ ‎17．（本题满分7分）先化简，再求值：，其中是整数,且 ‎18题 ‎18．（本题满分7分）如图，在平面直角坐标系中，点A，B，‎ C，P的坐标分别为(0，2)，(3，2)，(2，3)，(1，1)．‎ ‎ (1)请在图中画出△A′B′C′，使得△A′B′C′与△ABC 关于点P成中心对称；‎ ‎ (2)若一个二次函数的图像经过(1)中△A′B′C′的三个 ‎ 顶点，求此二次函数的关系式；‎ ‎19题 ‎19. （本题满分7分） 如图，为⊙O的弦，为劣 弧的中点，‎ ‎（1）若⊙O的半径为5，，求；‎ ‎（2）若，且点在⊙O的外部，判断 与⊙O的位置关系，并说明理由.‎ ‎20.（本题满分8分）某市为了解市民对已闭幕的某一博览会的总体印象，利用最新引进的“计算机辅助电话访问系统”‎ ‎（简称CATI系统），采取电脑随机抽样的方式，对本市年龄在16～65岁之间的居民，进行了400个电话抽样调查．并根据每个年龄段的抽查人数和该年龄段对博览会总体印象感到满意的人数绘制了下面的图(1)和图(2)（部分）‎ 图（2）‎ ‎16～20岁 ‎16%‎ ‎31～40岁 ‎20%‎ ‎51～60岁 ‎7%‎ ‎61～65岁 ‎3%‎ ‎21～30岁 ‎39%‎ ‎41～50岁 ‎15%‎ 根据上图提供的信息回答下列问题：‎ ‎（１）被抽查的居民中，人数最多的年龄段是　　　　　岁；‎ ‎（２）已知被抽查的400人中有83%的人对博览会总体印象感到满意，请你求出31～40岁年龄段的满意人数，并补全图(2)；‎ ‎（３）比较31～40岁和41～50岁这两个年龄段对博览会总体印象满意率的高低（四舍五入到1%）．注：某年龄段的满意率＝该年龄段满意人数该年龄段被抽查人数100％．‎ ‎21.（本题满分8分）直线AB//CD,∠ACD=72°﹒‎ ‎⑴用直尺和圆规作∠C的平分线CE,交AB于E,并在CD 上取一点F，使AC=AF，再连接AF,交CE于K；（要求保留作图痕迹，不必写出作法）‎ ‎⑵依据现有条件，直接写出图中所有相似的三角形﹒（图中不再增加字母和线段，不要求证明）﹒‎ 第22题 ‎22．(本题满分8分)一列火车由A市途经B、C两市到达D市．如图，其中A、B、C三市在同一直线上，D市在A市的北偏东45°方向，在B市的正北方向，在C市的北偏西60°方向，C市在A市的北偏东75°方向．已知B、D两市相距100km．问该火车从A市到D市共行驶了多少路程?（保留根号) ‎ 运动鞋 价格 甲 乙 进价（元/双）‎ m m﹣20‎ 售价（元/双）‎ ‎240‎ ‎160‎ ‎23、为了迎接“十•一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：‎ 已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．（1）求m的值；‎ ‎（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？‎ ‎（3）在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a（50＜a＜70）元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？（8分）‎ 第24题 ‎24．（本题满分9分）如图，在菱形ABCD中，AB=2cm，∠BAD=60°，E为CD边中点，点P从点A开始沿AC方向以每秒 cm的速度运动，同时，点Q从点D出发沿DB方向以每秒1cm的速度运动，当点P到达点C时，P，Q同时停止运动，设运动的时间为x秒.‎ ‎（1）当点P在线段AO上运动时.‎ ‎①请用含x的代数式表示OP的长度；‎ ‎②若记四边形PBEQ的面积为y，求y关于x的函数关系式（不要求写出自变量的取值范围）；‎ ‎（2）显然，当x=0时，四边形PBEQ即梯形ABED，请问，当P在线段AC的其他位置时，以P，B，E，Q为顶点的四边形能否成为梯形？若能，求出所有满足条件的x的值；若不能，请说明理由.‎ A2‎ B C 铅垂高 水平宽 h ‎ a ‎ ‎（图26-①）‎ ‎23、（本题满分10分） 阅读材料：如图26-①，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”（h）．我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半．‎ ‎（图26-②）‎ x C O y A B D ‎1‎ ‎1‎ 解答下列问题：如图26-②，抛物线顶点坐标为点（1，4），交轴于点（3，0），交轴于点．‎ ‎（1）求抛物线和直线的解析式；‎ ‎（2）求的铅垂高及；‎ ‎（3）设点是抛物线（在第一象限内）上的一个动点，是否存在一点，使，若存在，求出点的坐标；若不存在，请说明理由 ‎ 2014年中考数学模拟试卷 参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C D B A D B B B C A 一．仔细选一选（本题有10个小题，每小题3分，共30分．） ‎ 二．认真填一填 (本题有6个小题, 每小题4分, 共24分．)‎ ‎11 x>2 12． 4 13． 12 , ‎ ‎14. 15. 16. ‎ 三．全面答一答 (本题有8个小题, 共66分．) ‎ ‎17. (本题6分) 解:原式= ……… 3分 当a=－1时, …………….2分 原式= -1 …………….1分 ‎18. (本题6分) 解：(1)图略 ………… ………………………………3分 ‎ (2) ………… ……………………………3分 ‎19. (本题6分) (1)解： ∵为⊙O的弦，为劣弧的中点,‎ E ‎∴于E∴ ……1分 又 ∵ ∴ ‎ ‎∴ ……1分 在Rt△AEC中, ……1分 ‎ (2)AD与⊙O相切. ……1分 理由如下： ‎ ‎ ∵ ∴‎ ‎∵由（1）知 ∴ ∠C+∠BAC＝90°. ……1分 又∵ ∴ ……1分 ‎ ∴AD与⊙O相切. ‎ ‎20. (本题8分) (1) 被抽查的居民中，人数最多的年龄段是21~30岁 …………2分 ‎(2)总体印象感到满意的人数共有(人)‎ ‎31~40岁年龄段总体印象感到满意的人数是 ‎ ‎(人) …………………………………2分 图略 …………………………………1分 ‎(3) 31~40岁年龄段被抽人数是(人)‎ 总体印象的满意率是 ………………………1分 ‎41~50岁被抽到的人数是人,满意人数是53人, ‎ 总体印象的满意率是 ………………………1分 ‎ ∴41~50岁年龄段比31~40岁年龄段对博览会总体印象的满意率高 …………1分 ‎21. (本题8分) ‎ 解：⑴CE作法正确得2分，F点作法正确得1分，K点标注正确得1分；‎ ‎⑵△CKF∽△ACF∽△EAK;△CAK∽△CEA ‎ ‎(注：共4对相似三角形，每正确1对可各得1分)‎ ‎22. (本题10分)‎ 解:过点B分别作BE⊥CD于E，BF⊥AD于F．‎ 由题，∠BDE=60°，∠BCE=45°，∠BDF=45°，∠BAF=30°．………………2分 E F ‎ ∴DE=50，…………………………………1分 ‎…………………………………1分 ‎…………………………………1分 ‎∴…………………………………1分 ‎∵．…………………………………1分 ‎∴…………………………………1分 ‎∴． ……………1分 ‎∴该火车从A市到D市共行驶了（）km．………1分 ‎23.(本题10分) ‎ 解：（1）∵ 30 000÷5 000＝6, ∴ 能租出24间. ……………2分 ‎（2）设每间商铺的年租金增加x万元,则 ‎ （30－）×（10＋x）－（30－）×1－×0.5＝275， ………2分 ‎ ‎ 2 x 2－11x＋5＝0， ∴ x＝5或0.5， ‎ ‎∴ 每间商铺的年租金定为10.5万元或15万元. ……………2分 ‎（3）275万元不是最大年收益 ……………1分 ‎ 当每间商铺的年租金定为12.5万元或13万元. ……………2分 ‎ ‎ 达到最大年收益，最大是285万元 ……………1分 ‎ ‎24．（本题12分）‎ ‎. 解：（1）①由题意得∠BAO=30°，AC⊥BD ‎ ∵AB=2 ∴OB=OD=1，OA=OC=‎ ‎ ∴OP= ……………2分 ‎ ②过点E作EH⊥BD，则EH为△COD的中位线 ‎ ∴ ∵DQ=x ∴BQ=2-x ‎ ∴ …………………………1分 ‎ …………………………1分 ‎∴ …………………………2分 ‎（2）能成为梯形，分三种情况：‎ ‎ 当PQ∥BE时，∠PQO=∠DBE=30°‎ ‎ ∴‎ ‎ 即 ∴x=‎ 此时PB不平行QE，‎ ‎∴x=时，四边形PBEQ为梯形. ………………………2分 当PE∥BQ时，P为OC中点 ‎ ∴AP=，即 ‎ ∴‎ 此时，BQ=2-x=≠PE，‎ ‎∴x=时，四边形PEQB为梯形. …………………2分 当EQ∥BP时，△QEH∽△BPO ‎ ∴ ∴‎ ‎ ∴x=1（x=0舍去）‎ ‎ 此时，BQ不平行于PE，‎ ‎∴x=1时，四边形PEQB为梯形. ………………………………2分 综上所述，当x=或或1时，以P，B，E，Q为顶点的四边形是梯形. ‎ ‎23．解：（1）设抛物线的解析式为： 把A（3，0）代入解析式求得 所以设直线AB的解析式为：‎ 由求得B点的坐标为把，代入中 解得：所以 ‎（2）因为C点坐标为（1，4）所以当x＝１时，y1＝4，y2＝2‎ 所以CD＝4-2＝2 （平方单位）‎ ‎（3）假设存在符合条件的点P，设P点的横坐标为x，△PAB的铅垂高为h，则 ‎ 由S△PAB=S△CAB 得：化简得： 解得， 将代入中，解得P点坐标为 ‎ ‎ 2011年中考数学模拟试卷 答题卷 一. 仔细选一选 (本题有10个小题, 每小题3分, 共30分) ‎ ‎6 7 8 9 10‎ ‎ [A] [A] [A] [A] [A]‎ ‎ [B] [B] [B] [B] [B]‎ ‎ [C] [C] [C] [C] [C]‎ ‎ [D] [D] [D] [D] [D]‎ ‎1 2 3 4 5‎ ‎ [A] [A] [A] [A] [A]‎ ‎ [B] [B] [B] [B] [B]‎ ‎ [C] [C] [C] [C] [C]‎ ‎ [D] [D] [D] [D] [D]‎ 二、认真填一填（每小题4分，共24分）‎ ‎11． 12. 13． 14． 15． 16． ‎ ‎17．(本题满分6分)‎ 先化简，再求值：，其中是整数,且 三、全面答一答(共66分)‎ ‎18．(本题满分6分)‎ ‎ ‎ ‎19．(本题满分6分)‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎20．(本题满分8分) ‎ ‎（１）被抽查的居民中，人数最多的年龄段是　　　　　岁；‎ ‎21.(本题满分8分) ‎ ‎22．(本题满分10分)‎ ‎ ‎ ‎ MM们  ‎ ‎23．本题满分10分)‎ ‎ ‎ ‎ ‎ ‎24.（本题满分12分）‎ ‎ ‎ ‎ ‎