初三中考总复习——图形变换
初三中考总复习——图形变换
西城外国语学校 袁慎鹏
图形变换是对几何图形认识方法上的一种改变.通过平移、轴对称、旋转变换达到复杂图形简单化、一般图形特殊化,分散条件集中化的目的.从图形变换的角度思考问题,可以整体把握图形的性质,特别是可以帮助我们从更高的层次理解平行线、截长补短、倍长中线等常用辅助线的作用,使问题解决更加简洁明确.当图形运动变化的时候,从运动变换的角度更容易发现不变量和特殊图形.
一、《考试说明》的要求:
考试内容
考试要求
A
B
C
图形的变化
图形的平移
了解平移的概念;理解平移的基本性质.
能画出简单平面图形平移后的图形;能利用平移的性质解决有关简单问题.
运用平移的有关内容解决有关问题
图形的轴对称
了解轴对称的概念;理解了解平移的概念;了解轴对称图形的概念.
能画出简单平面图形关于给定对称轴的对称图形;探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质;能利用轴对称的性质解决有关简单问题.
运用轴对称的有关内容解决有关问题
轴对称旋转
认识平面图形关于旋转中心的旋转;理解旋转的基本性质;理解中心对称、中心对称图形的概念;理解中心对称的性质.
能画出简单平面图形关于给定旋转中心的旋转图形;探索线段、平行四边形、正多边形、圆的中心对称性质;能利用旋转的性质解决有关简单问题.
运用旋转的有关内容解决有关问题
变化:
1.顺序有变化,符合学生学习的顺序;
2.变换的性质比较笼统没有2014年的说明具体;
3.“作图”变为“画图”,画图的要求更加具体;
4.基本的轴对称图形由六个变为五个,删掉了“等腰梯形”;
5.C级要求的“解决简单问题”统一变为“解决有关问题”.
二、图形变换在近6年中考中的分布及呈现方式:
近6年的中考中,变换在选择、填空、操作题、第23题、第24题、第25题中都有出现过,主要的考察方式有:辨别轴对称图形与中心对称图形;通过阅读理解获取有效信息,选择合适的的变换对图形进行重新构造从而解决问题;把函数的图象进行变换,要求发现平移后的函数与原函数之关系;应用变换的思想综合运用几何知识添加适当的辅助线解决问题.
三、复习建议:
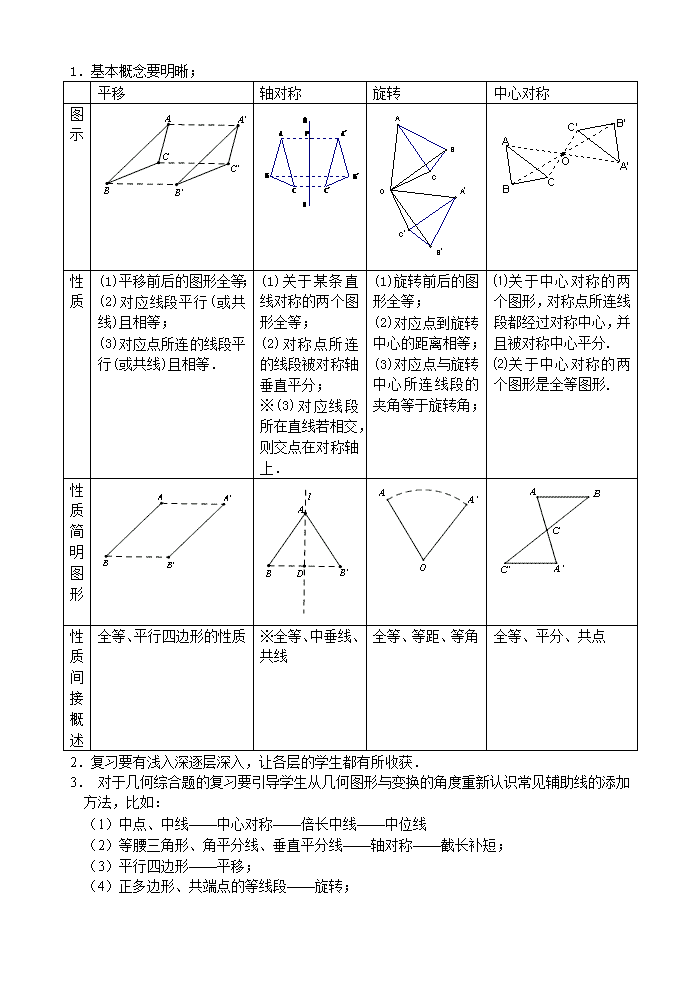
1.基本概念要明晰;
平移
轴对称
旋转
中心对称
图示
性质
(1)平移前后的图形全等;
(2)对应线段平行(或共线)且相等;
(3)对应点所连的线段平行(或共线)且相等.
(1)关于某条直线对称的两个图形全等;
(2)对称点所连的线段被对称轴垂直平分;
※(3)对应线段所在直线若相交,则交点在对称轴上.
(1)旋转前后的图形全等;
(2)对应点到旋转中心的距离相等;
(3)对应点与旋转中心所连线段的夹角等于旋转角;
⑴关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心平分.
⑵关于中心对称的两个图形是全等图形.
性质简明图形
性质间接概述
全等、平行四边形的性质
※全等、中垂线、共线
全等、等距、等角
全等、平分、共点
2.复习要有浅入深逐层深入,让各层的学生都有所收获.
3. 对于几何综合题的复习要引导学生从几何图形与变换的角度重新认识常见辅助线的添加方法,比如:
(1)中点、中线——中心对称——倍长中线——中位线
(2)等腰三角形、角平分线、垂直平分线——轴对称——截长补短;
(3)平行四边形——平移;
(4)正多边形、共端点的等线段——旋转;
4.对于坐标系中研究函数图象的平移和对称的问题要引导学生抓住问题的本质,把该问题转化函数图象上点的变换问题,进而进一步转化为函数图象上关键点的变换问题.
四、第一轮复习安排和例题
共用三个课时,第一课时:三种变换的概念和性质的简单应用;第二课时,作图和操作问
题;第三课时:综合.
例1(2013北京) 下列图形中,是中心对称图形但不是轴对称图形的是( )
学生存在的问题:审题只看见是什么,忽略不是什么;旋转对称与中心对称易混淆;怕文字表述的图形.
例2如图,Rt△ABC中,∠ACB=90°,AC=2cm,.将△ABC沿AB边所在直线向右
平移,记平移后它的对应三角形为△DEF.
(1)若将△ABC沿直线AB向右平移3 cm,求此时梯形CAEF的面积;【答案】
(2)若使平移后得到的△CDF是直角三角形,
则△ABC平移的距离应为______cm.【答案】1或4
学生存在的问题:弄不清3cm是那条线段的长,不会分类.
例3(2011上海)Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0°
3时,两个正方形无公共点。
3. (2014平谷二模)(1)如图1,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,且CE=AB,BE=CD,连结AE、DE、AD,则△ADE的形状是_________________________.
(2)如图2,在,D、E分别为AB、AC上的点,连结BE、CD,两线交于点P.
①当BD=AC,CE=AD时,在图中补全图形,猜想的度数并给予证明.
②当时, 的度数____________________.
4.(07北京)如图,已知.
(1)请你在边上分别取两点(的中点除外),连结,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使(1)成立的相应条件,证明AB+AC>AD+AE.
专题二、轴对称变换.
5.(2014怀柔二模)如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆被覆盖部分(阴影部分)的面积为_____________.
6.(1)如图,在直角坐标系中,将矩形OABC沿
OB对折,使点A落在点处,若,
,则点的坐标是多少?
(2)如图,把矩形纸片OABC放入平面直角坐
标系中,使OA、OC分别落在x轴、y轴上,
连结OB,将纸片OABC沿OB折叠,使点A落在的位置,若,,则点的坐标是多少?
7. (2012浙江绍兴)如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交与点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn﹣1Dn﹣2的中点为Dn﹣1,第n次将纸片折叠,使点A与点Dn﹣1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )
A. B. C. D.
8. (2012江苏南京)如图,菱形纸片ABCD中,
∠A=600,将纸片折叠,点A、D分别落在A’、D’处,
且A’D’经过B,EF为折痕,当D’FCD时,的
值为( )
A. B. C. D.
9.(2012山东德州)如图所示,现有一张边长为4的正方形纸片,点P为正方形AD边
上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,
PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变
化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
10.(2014西城二模)在△ABC,∠BAC为锐角,AB>AC, AD平分∠BAC交BC于点D.
(1)如图1,若△ABC是等腰直角三角形,直接写出线段AC,CD,AB之间的数量关系;
(2)BC的垂直平分线交AD延长线于点E,交BC于点F.
①如图2,若∠ABE=60°,判断AC,CE,AB之间有怎样的数量关系并加以证明;
②如图3,若,求∠BAC的度数.
专题三、旋转变换
11.(2014大兴二模) 已知:E是线段AC上一点,AE=AB,过点E作直线EF,在EF上取一点D,使得∠EDB=∠EAB,联结AD.
(1)若直线EF与线段AB相交于点P,当∠EAB=60°时,如图1,求证:ED =AD+BD;
(2)若直线EF与线段AB相交于点P,当∠EAB= α(0º﹤α﹤90º)时,如图2,请你直接写出线段ED、AD、BD之间的数量关系(用含α的式子表示);
(3)若直线EF与线段AB不相交,当∠EAB=90°时,如图3,请你补全图形,写出线段ED、AD、BD之间的数量关系,并证明你的结论.
12. (2014房山二模) 边长为2的正方形的两顶点、分别在正方形EFGH的两边、上(如图1),现将正方形绕点顺时针旋转,当点第一次落在上时停止旋转,旋转过程中,边交于点,边交于点.
(1)求边在旋转过程中所扫过的面积;
(2)旋转过程中,当和平行时(如图2),求正方形旋转的度数;
(3)如图3,设的周长为,在旋转正方形的过程中,值是否有变化?请证明你的结论.
13. (2014门头沟二模) 在△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,M是BC边中点中点,连接MD和ME
(1)如图1所示,若AB=AC,则MD和ME的数量关系是
(2)如图2所示,若AB≠AC其他条件不变,则MD和ME具有怎样的数量和位置关系?请给出证明过程;
(3) 在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,M是BC的中点,连接MD和ME,请在图3中补全图形,并直接判断△MED的形状.
图1 图2 图3
14. (丰台二模)如图1,在中,∠ACB=90º,BC=2,∠A=30°,点E,F分别是线段
BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是________, ________.
(2)如图2,当绕点顺时针旋转时(),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当绕点顺时针旋转时(),延长交于点,如果,求旋转角的度数.
15.(2014石景山二模)将△绕点顺时针旋转得到△,的延长线与
相交于点,连接.
(1)如图1,若==,,请直接写出与的数量关系;
(2)如图2,若<=,,猜想线段与的数量关系,并证明你的猜想;
(3)如图3,若<,(为常数),请直接写出的值
(用含、的式子表示).
16.(2011丰台)已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD. 探究下列问题:(1)如图1,当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD= ;
(2)如图2,当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD= ;
(3)如图3,当∠ACB变化,且点D与点C位于直线AB的两侧时,求 CD的最大值及相
应的∠ACB的度数.
17. (2011浙江义乌)如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面
积为S,求S关于x的函数关系
专题四、中心对称变换
18.已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中BA=BC,DA=DE,联结EC,取EC的中点M,联结BM和DM.
(1)如图1,如果点D、E分别在边AC、AB上,那么BM、DM的数量关系与位置关系是 ;
(2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.
图1 图2
19. 如图,Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以AB、AC为边作等边△ABE和△ACD,连结ED交AB于F,求证:EF=FD.
20.(08北京)请阅读下列材料:
问题:如图1,在菱形和菱形中,点在同一条直线上,是线段的中点,连结.若,探究与的位置关系及的值.
小聪同学的思路是:延长交于点,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段与的位置关系及的值;
(2)将图1中的菱形绕点顺时针旋转,使菱形的对角线恰好与菱形
的边在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中,将菱形绕点顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含的式子表示).
专题五、操作题
21.(丰台二模)阅读下列材料:
已知:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造□APBQ,求对角线PQ的最小值及此时的值是多少.
在解决这个问题时,小明联想到在学习平行线间的距离时所了解的知识:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.
进而,小明构造出了如图2的辅助线,并求得PQ的最小值为3.
参考小明的做法,解决以下问题:
(1)继续完成阅读材料中的问题:当PQ的长度最小时,_______;
(2)如图3,延长PA到点E,使AE=nPA(n为大于0的常数).以PE,PB为边作□PBQE,
那么对角线PQ的最小值为 ,此时_______;
(3)如图4,如果P为AB边上的一动点,延长PA到点E,使AE=nPA(n为大于0的常数),以PE,PC为边作□PCQE,那么对角线PQ的最小值为______,此时_______.
22.(密云二模)如图,将矩形纸片ABCD按如下顺序折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);沿GH
折叠,使点C落在DH上的C处(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图⑥).
(1)求图②中∠BCB′的大小;
(2)图⑥中的△GCC′是正三角形吗?请说明理由.
23. (2014平谷二模)如图1,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小,做法是:作点B关于直线l的对称点B′,连接AB′,与直线l的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
(1)如图2,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.做法是:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,这点就是所求的点P,故BP+PE的最小值为 ;
(2)如图3,已知⊙O的直径CD为2,的度数为60°,点B是的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为 ;
(3)如图4,点P是四边形ABCD内一点,BP=m,,分别在边AB、BC上作出点M、N,使的周长最小,求出这个最小值(用含m、的代数式表示).
专题五、函数与变换
24. (2014房山二模)已知关于的一元二次方程有实数根,为正整数.
(1)求的值;
(2)当此方程有两个不为0的整数根时,将关于的二次函数的图象向下平移2个单位,求平移后的函数图象的解析式;
(3)在(2)的条件下,将平移后的二次函数图象位于轴左侧的部分沿轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线与图象G有3个公共点时,请你直接写出的取值范围.
25. (丰台二模)如图,经过原点的抛物线()与x轴的另一交点为A,过点P(1, )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
(1)当b=4时,求点A的坐标及BC的长;
(2)连结CA,求b的适当的值,使得CA⊥CP;
(3)当b=6时,如图2,将△CBP绕着点C按逆时针方向旋转,得到△CB’P’,CP与抛物线对称轴的交点为E,点M为线段B’P’(包含端点)上任意一点,请直接写出线段EM长度的取值范围.
26.(2014海淀二模)已知关于的方程:①和②,其中.
(1)求证:方程①总有两个不相等的实数根;
(2)设二次函数的图象与轴交于、两点(点在点的左侧),将、
两点按照相同的方式平移后,点落在点处,点落在点处,若点的横坐标恰好是方程②的一个根,求的值;
(3)设二次函数,在(2)的条件下, 函数,的图象位于直线左侧的部分与直线()交于两点,当向上平移直线时,交点位置随之变化,若交点间的距离始终不变,则的值是________________.
27.(2014平谷二模)已知关于x的一元二次方程.
(1)求证:无论m取任何实数时,方程总有实数根;
(2)关于x的二次函数的图象经过和两点.
①求这个二次函数的解析式;
②把①中的抛物线沿x轴翻折后,再向左平移2个单位,向上平移8个单位得到抛物线.设抛物线交x轴于M、N两点(点M在点N的左侧),点P(a,b)为抛物线在x轴上方部分图象上的一个动点.当∠MPN≤45°时,直接写出a的取值范围.
28.(2012北京)已知二次函数在与的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数的图象与二次函数的图象都经过点A(,),求m与k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧 ),将二次函数的图象B,C间的部分(含点B和点C)向左平移n()个单位后得到的图象记为G
,同时将(2)中得到的直线向上平移n个单位.请结合图象回答:平移后的直线与图象G有公共点时,n的取值范围.
专题六、复合变换
29.已知,正方形ABCD的边长为1,直线//直线,与之间的距离为1,与
正方形ABCD的边总有交点.
(1)如图1,当于点A,,交边DC、BC分别于E、F时,求△EFC
的周长;
(2)把图1中的与同时向右平移x,得到图2,问△EFC与△AMN的周长的和是否
随x的变化而变化,若不变,求出△EFC与△AMN周长的和;若变化,请说明理由;
(3)把图2中的正方形饶点A逆时针旋转,得到图3,问△EFC与△AMN周长的和是否随的变化而变化,若不变,求出的周长的和;若变化,请说明理由.