2017河南中考数学模拟卷三

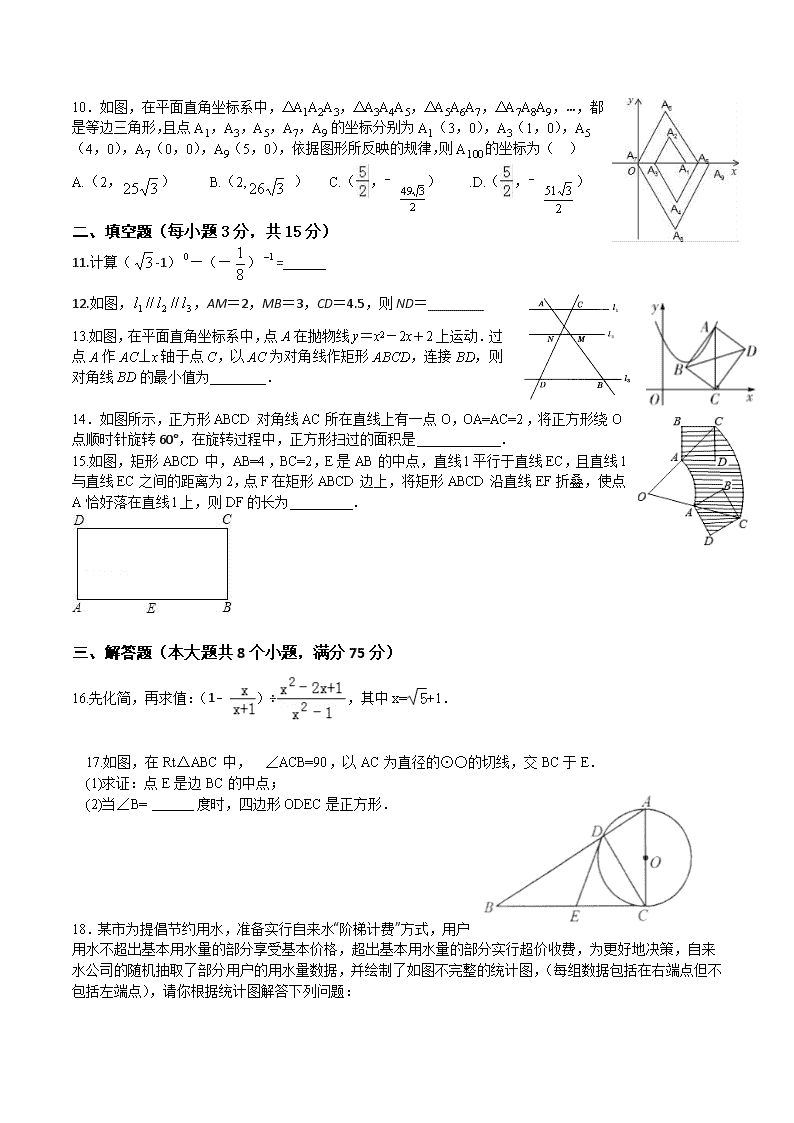
2017河南中考数学模拟卷三

‎2017河南中考数学模拟卷（三）‎ 一、选择题（下列各题的备选答案中，只有一个是正确的。每小题3分，共30分）‎ ‎1．下列各数中，最小的数是（　　）‎ A．0 B． C．﹣3 D．﹣2‎ ‎2．由六个相同的立方体搭成的几何体如图所示，则它的左视图是（　　）‎ A． B． C． D．‎ ‎3．空气的密度为0.00129g/cm3，0.00129这个数用科学记数法可表示为（　　）‎ A．0.129×10﹣2 B．1.29×10﹣2 C．1.29×10﹣3 D．12.9×10﹣1‎ ‎4．如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（　　）‎ A．50° B．100° C．120° D．130°‎ ‎5．2016年6月4日﹣5日贵州省第九届“贵青杯”﹣“乐韵华彩”全省中小学生器乐交流比赛在省青少年活动中心举行，有45支队参赛，他们参赛的成绩各不相同，要取前23名获奖，某代表队已经知道了自己的成绩，他们想知道自己是否获奖，只需再知道这45支队成绩的（　　）‎ A．中位数 B．平均数 C．最高分 D．方差 ‎6．如图，A，B两点在反比例函数y=的图象上，C、D两点在反比例函数y=的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF=，则k2﹣k1=（　　）‎ A．4 B． C． D．6‎ ‎7．有一枚均匀的正方体骰子，骰子各个面上的点数分别为1，2，3，4，5，6，若任意抛掷一次骰子，朝上的面的点数记为x，计算|x﹣4|，则其结果恰为2的概率是（　　）‎ A． B． C． D．‎ ‎8．如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（　　）‎ ‎①AD是∠BAC的平分线 ‎ ‎②∠ADC=60°‎ ‎③点D在AB的垂直平分线上 ‎ ‎④AB=2AC．‎ A．1 B．2 C．3 D．4‎ ‎9. 已知3是关于x的方程x2﹣（m+1）x+2m=0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长，则△ABC的周长为（　　）‎ A．7 B．10 C．11 D．10或11‎ ‎10．如图，在平面直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7，△A7A8A9，…，都是等边三角形，且点A1，A3，A5，A7，A9的坐标分别为A1（3，0），A3（1，0），A5（4，0），A7（0，0），A9（5，0），依据图形所反映的规律，则A100的坐标为（ ）‎ A.（2，） B.（2, ） C.（，﹣） .D.（，﹣）‎ 二、填空题（每小题3分，共15分）‎ ‎11.计算（-1）—（—）= ‎ ‎12.如图，，AM＝2，MB＝3，CD＝4.5，则ND＝________‎ ‎13.如图，在平面直角坐标系中，点A在抛物线y＝x2－2x＋2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连接BD，则对角线BD的最小值为________．‎ ‎14．如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是　　　　　　．‎ ‎15.如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为　 　．‎ 三、解答题（本大题共8个小题，满分75分）‎ ‎16.先化简，再求值：（1﹣）÷，其中x=+1．‎ ‎17.如图，在Rt△ABC中，Ð∠ACB=90，以AC为直径的⊙○的切线，交BC于E． ‎ ‎(1)求证：点E是边BC的中点； ‎ ‎(2)当∠B=   度时，四边形ODEC是正方形．         ‎ ‎18．某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费，为更好地决策，自来水公司的随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图，（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题：‎ ‎（1）此次抽样调查的样本容量是______．‎ ‎（2）补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数．‎ ‎（3）如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？‎ ‎19.如图，海中一小岛上有一个观测点A，某天上午9：00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行。当天上午9：30观测到该渔船在观测点A的北偏西60°方向上的C处。若该渔船的速度为每小时30海里，在此航行过程中，问该渔船从B处开始航行多少小时，离观测点A的距离最近?(计算结果用根号表示，不取近似值)。 ‎ ‎20．阅读下面材料：‎ ‎ 上课时李老师提出这样一个问题：对于任意实数，关于的不等式恒成立，求的取值范围．‎ 小捷的思路是：原不等式等价于，设函数，，画出两个函数的图象的示意图，于是原问题转化为函数的图象在的图象上方时的取值范围．‎ 请结合小捷的思路回答：‎ 对于任意实数，关于的不等式恒成立，则的取值范 围是___________．‎ 参考小捷思考问题的方法，解决问题：‎ 关于的方程在范围内有两个解，求的取值范围．‎ ‎21. 某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元，已知购买一个B种品牌的足球比购买一个A钟品牌的足球多花30元．‎ ‎（1）求购买一个A种品牌、一个B种品牌的足球各需多少元．‎ ‎（2）学校为了响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高4元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%，且保证这次购买的B种品牌足球不少于23个，则这次学校有哪几种购买方案？‎ ‎（3）请你求出学校在第二次购买活动中最多需要多少资金？‎ ‎22．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．‎ ‎（1）如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；‎ ‎（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；‎ ‎（3）如图3，若α=45°，点E在BC的延长线上，则等式DE2=BD2+CE2还能成立吗？请说明理由．‎ ‎23.如图，已知抛物线y=ax2 +bx +c的顶点D的坐标为(1，)，且与x轴交于A，B两点，与y轴交于C点，A点的坐标为(4，0)．P点是抛物线上的一个动点，且横坐标为m．‎ ‎（1）求抛物线所对应的二次函数的表达式．‎ ‎（2）若动点P满足∠PAO不大于45°，求P点的横坐标m的取值范围．‎ ‎（3）是否存在P点，使∠PAC=∠BCO？若存在，请直接写出点P的坐标；若不存在，请说明理由．‎