中考数学模拟测试卷二

中考数学模拟测试卷二

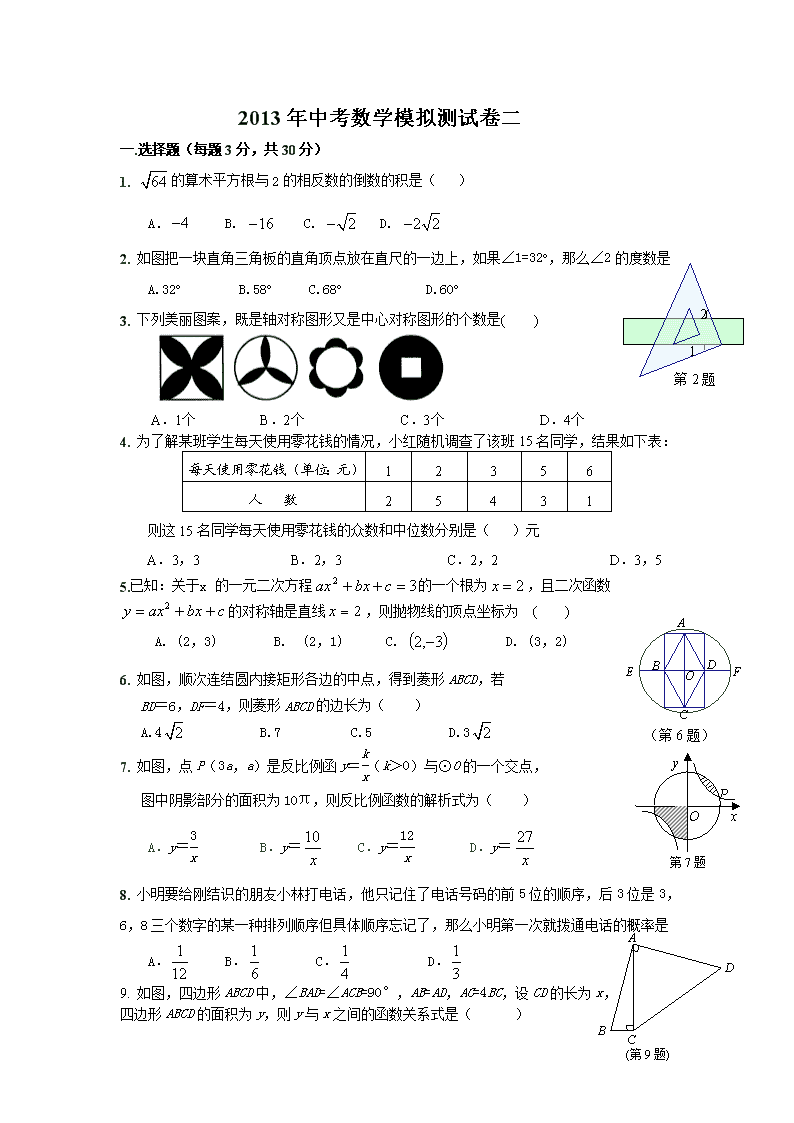
‎2013年中考数学模拟测试卷二 一.选择题（每题3分，共30分）‎ ‎1. 的算术平方根与2的相反数的倒数的积是（ ）‎ ‎ A． B. C. D. ‎ ‎2‎ ‎1‎ 第2题 ‎2. 如图把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=32o，那么∠2的度数是 A.32o B.58o C.68o D.60o ‎ ‎3. 下列美丽图案，既是轴对称图形又是中心对称图形的个数是( )‎ A．1个 B．2个 C．3个 D．4个 ‎4. 为了解某班学生每天使用零花钱的情况，小红随机调查了该班15名同学，结果如下表：‎ 每天使用零花钱（单位：元）‎ ‎1‎ ‎2‎ ‎3‎ ‎5‎ ‎6‎ 人 数 ‎2‎ ‎5‎ ‎4‎ ‎3‎ ‎1‎ 则这15名同学每天使用零花钱的众数和中位数分别是（ ）元 A．3，3 B．2，3 C．2，2 D．3，5‎ A B C D E F O ‎（第6题）‎ ‎5. 已知：关于x的一元二次方程的一个根为，且二次函数的对称轴是直线，则抛物线的顶点坐标为 ( )‎ ‎ A. (2，3) B. (2，1) C. D. (3，2) ‎ ‎6. 如图，顺次连结圆内接矩形各边的中点，得到菱形ABCD，若 BD＝6，DF＝4，则菱形ABCD的边长为（ ）‎ A.4 B.7 C.5 D.3‎ x O y P 第7题 ‎7. 如图，点P（3a，a）是反比例函y＝（k＞0）与⊙O的一个交点，‎ 图中阴影部分的面积为10π，则反比例函数的解析式为（ ）‎ A．y＝ B．y＝ C．y＝ D．y＝‎ ‎(第9题)‎ A B C D ‎8. 小明要给刚结识的朋友小林打电话，他只记住了电话号码的前5位的顺序，后3位是3，6，8三个数字的某一种排列顺序但具体顺序忘记了，那么小明第一次就拨通电话的概率是 A． B． C． D．‎ ‎9. 如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，‎ 四边形ABCD的面积为y，则y与x之间的函数关系式是（　 　）‎ A． B． C． D．‎ ‎10.如图，O是正方形ABCD的对角线BD上一点，⊙O与边AB,BC都相切，点E,F分别在AD,DC上，现将△DEF沿着EF对折，折痕EF与⊙O相切，此时点D恰好落在圆心O处。若DE=2，则正方形ABCD的边长是（ ）‎ ‎ A.3 B.4 C. D.‎ 二.填空题（每题4分，共24分）‎ ‎11. 分解因式： ．‎ ‎12. 为保护水资源，某社区新建了雨水再生工程，再生水利用量达58600立方米/年。这个数据用科学记数法表示为 。（保留两个有效数字）‎ ‎（第14题图）‎ ‎13. 若，且一元二次方程有两个实数根，则的取值范围是________；‎ ‎14.已知双曲线，的部分图象如图所示，是轴正半轴上 过点作∥轴，分别交两个图象于点．若，则 ．‎ ‎15. 亮亮想制作一个圆锥模型，这个模型的侧面是用一个半径为9cm,圆心角为240°的扇形铁皮制作的，再用一块圆形铁皮做底，请你帮他计算这块圆形铁皮的半径为 cm。‎ ‎16.已知一个半圆形工件，未搬动前如图所示，直径平行于地面放置，搬动时为了保护圆弧部分不受损伤，先将半圆作如图所示的无滑动翻转，使它的直径紧贴地面，再将它沿地面平移50米，半圆的直径为4米，则圆心O所经过的路线长是___ ______．‎ O O O O l ‎ ‎ 三.解答题(66分)‎ ‎17. （6分）计算： －22+(tan60o－1)×+(－)－2+(－π)o－|2－|‎ ‎18. （7分）解不等式组： 并把它的解集在数轴上表示出来．‎ ‎19.（7分） 先化简，再求值:÷（2x — ）其中，x=+1 ‎ ‎20. (8分)已知关于x的方程．‎ ‎（1）若这个方程有实数根，求k的取值范围；‎ ‎（2）若这个方程有一个根为1，求k的值；‎ ‎（3）若以方程的两个根为横坐标、纵坐标的点恰在反比例函数的图象上，求满足条件的m的最小值．‎ ‎21.（8分）已知，如图，直线MN交⊙O于A,B两点，AC是直径，AD平分CAM交⊙O于D，过D作DE⊥MN于E．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若cm，cm，求⊙O的半径.‎ ‎22.（8分） 初中生对待学习的态度一直是教育工作者关注的问题之一．‎ 为此，某区教委对该区部分学校的八年级学生对待学习的态度 进行了一次抽样调查（把学习态度分为三个层级，A级：对学 习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴 趣），并将调查结果绘制成图①和图②的统计图（不完整）．‎ 请根据图中提供的信息，解答下列问题：‎ ‎（1）此次抽样调查中，共调查了 名学生；‎ ‎（2）将图①补充完整；‎ ‎（3）求出图②中C级所占的圆心角的度数；‎ ‎（4）根据抽样调查结果，请你估计该区近20000名初中生中大 约有多少名学生学习态度达标（达标包括A级和B级）？‎ ‎23.(10分) 为发展“低碳经济”，某单位进行技术革新, 让可再生资源重新利用. 从今年1月1日开始,该单位每月再生资源处理量y（吨）与月份x之间成如下一次函数关系：‎ 月份x ‎ ‎1‎ ‎2‎ 再生资源处理量y（吨）‎ ‎40‎ ‎50‎ 月处理成本z（元）与每月再生资源处理量y（吨）之间的函数关系可近似地表示为：‎ ‎ z =,每处理一吨再生资源得到的新产品的售价定为100元.‎ ‎（1）该单位哪个月获得利润最大？最大是多少？‎ ‎（2）随着人们环保意识的增加，该单位需求的可再生资源数量受限。今年三、四月份的再生资源处理量都比二月份减少了m% ,该新产品的产量也随之减少，其售价都比二月份的售价增加了0.6m%.五月份，该单位得到国家科委的技术支持，使月处理成本比二月份的降低了20% .如果该单位在保持三月份的再生资源处理量和新产品售价的基础上，其利润是二月份的利润的一样,求m ．( m保留整数) （‎ ‎24.（12分0如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（，0）、（0，4），抛物线经过B点，且顶点在直线上．‎ ‎（1）求抛物线对应的函数关系式；‎ ‎（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；‎ ‎（3）若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．‎ 解：（1）由题意，可设所求抛物线对应的函数关系式为 …（1分）‎ ‎ ∴‎ ‎ ∴ ……………………………………………………………（3分）‎ ‎ ∴所求函数关系式为： …………（4分）‎ ‎ （2）在Rt△ABO中，OA=3，OB=4，‎ ‎∴‎ ‎∵四边形ABCD是菱形 ‎∴BC=CD=DA=AB=5 ……………………………………（5分）‎ ‎∴C、D两点的坐标分别是（5，4）、（2，0）． …………（6分）‎ 当时，‎ 当时，‎ ‎∴点C和点D在所求抛物线上． …………………………（7分）‎ ‎（3）设直线CD对应的函数关系式为，则 解得：．‎ ‎∴ ………（9分）‎ ‎∵MN∥y轴，M点的横坐标为t，‎ ‎∴N点的横坐标也为t．‎ 则， ，……………………（10分）‎ ‎∴‎ ‎∵， ∴当时，，‎ 此时点M的坐标为（，）． ………………………………（12分）‎