景新中学初三数学中考模拟试题及答案
景新中学2008年初三数学中考模拟试题(1)
(考试时间90分钟,满分100分)
题号
一
二
三
总分
1-10
11-15
16
17
18
19
20
21
22
23
得分
一、选择题:(本大题共10题,每小题3分,共30分)
每小题给出四个答案,其中只有一个符合题目的要求,请把选出的答案编号填在下面的答题表一内,否则不给分.
答题表一
题号
1
2
3
4
5
6
7
8
9
10
答案
1、下列说法正确的是
A. 若x2=2,则x= B. 若 -3x>2,则x<
C. 若分式的值为零,则x= -1 D. 若(x+1) (x-2) =3,则x= -1,x=2
2、下列各式正确的是
A. = a+3 B. C. D.
3、不等式组的解集是
A.x>3 B.-1
-1时,y随x增大而增大 D、与x轴无交点
8、在化学反应A+B==C+D中,已知25克A与10克B恰好完全反应,且生成5克C;若
完全反应后,有6克D生成时,那么参加反应的A是
A. 5克 B. 10克 C. 20克 D. 25克
9、用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如
图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为
A. 7 B. 8 C. 10 D. 11
(第9题图)
北
南
东
西
B
C
A
(第10题图)
(主视图)
(俯视图)
10、如图,小鹏从A点沿北偏西60º方向走10m到点B,再从点B向正南方向走20m
到点C,此时C、A两点间的距离为
A、5m B、10 m C、10m D、15m
二、填空题:(本大题共5小题,每小题3分,共15分,请将答案填入答题表二内,否则不给分)
答题表二
题号
11
12
13
14
15
答案
11、将 (2×105 )(8×102 ) 的运算结果用科学计数法表示为 ▲ .
12.已知m、n为常数,且满足:ma2b+3anb= -2a2b,则m + n的值为 ▲ .
13、若一组数据2,-1,0,a,3的极差为5,则a的值是 ▲ .
A
E
B
C
D
14、如图,在口ABCD中,CE⊥AB于点E.如果∠A=130º,则∠BCE= ▲ 度.
15、观察下列等式:①=2;②=3;
③=4;……. 请你根据发现的规律写出第n个等式 ▲ .
三、解答题:(共7题,共55分)
16、(本题6分)解方程:
解:
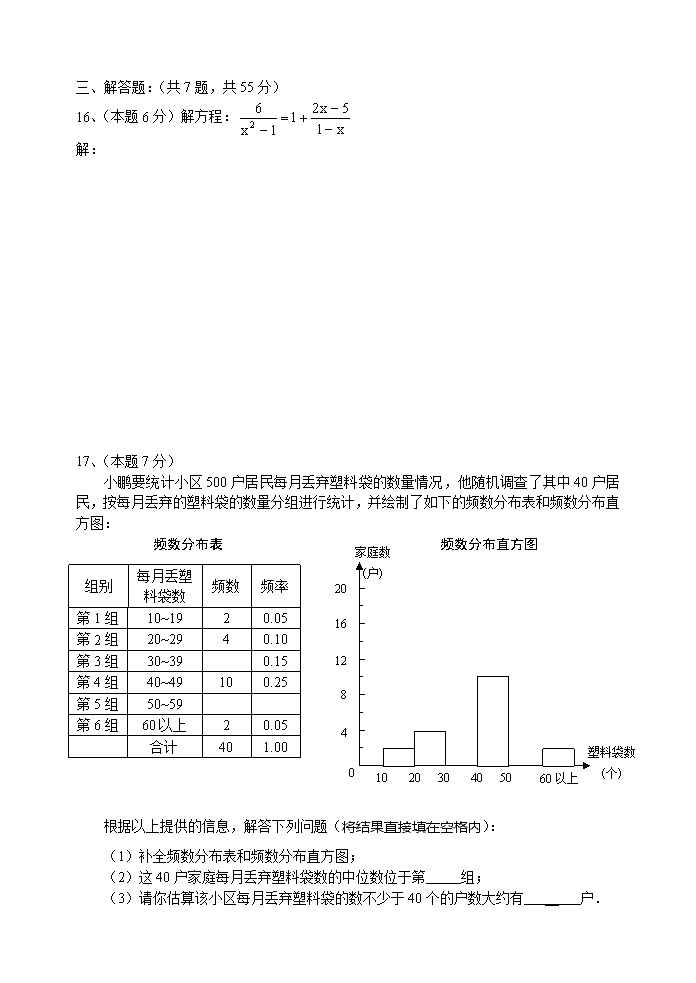
17、(本题7分)
小鹏要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
0
60以上
10
20
30
40
50
4
8
12
16
20
塑料袋数
(个)
家庭数
(户)
频数分布表 频数分布直方图
组别
每月丢塑料袋数
频数
频率
第1组
10~19
2
0.05
第2组
20~29
4
0.10
第3组
30~39
0.15
第4组
40~49
10
0.25
第5组
50~59
第6组
60以上
2
0.05
合计
40
1.00
根据以上提供的信息,解答下列问题(将结果直接填在空格内):
(1)补全频数分布表和频数分布直方图;
(2)这40户家庭每月丢弃塑料袋数的中位数位于第 组;
(3)请你估算该小区每月丢弃塑料袋的数不少于40个的户数大约有 __ 户.
18、(本题7分)
有一枚均匀的硬币,一面图案是“数字”,另一面是“菊花”. 小鹏任意掷该硬币三次,请利用画树状图或列表的方法解答下列问题:
(1)求三次全是“数字”面朝上的概率;
(2)求有且仅有两次“菊花”面朝上的概率.
解:
19、(本题7分)
商场某种商品的原售价比进价高50%. 节日里为促销,商场将这种商品按原售价打八折销售,且每卖出一件这种商品,商场仍可获利20元,求这种商品的进价.
解:
20、(本题8分)
如图,在正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连结AD、CD。
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C_________、D__________;
②⊙D的半径= ________(结果保留根号);∠ADC=______度。
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面的面积为________.
A
B
C
O
21、(本题9分)
如图,以⊙O的半径OA为直径作一个⊙P,点B在⊙P上,连结OB并延长交⊙O的切线AD于点D. 连结AB并延长,交⊙O于点C,连结CD. 已知OA=4,OB=2.
A
O
C
B
D
P·
(1)求∠ADC的度数;
(2)求证:CD是⊙O的切线.
22、(本题11分)
对称轴是x = 1的抛物线与x轴交于A、B两点,与y轴交于点C,作直线BC,如图所示.;点P是线段OB上不与点O、B重合的一个动点,过点P作y轴的平行线,交直线BC于点D,交抛物线于点E,连结CE、OD. 已知OA:OB=1:3,tan∠DBP=1.
(1)求抛物线的函数表达式;
(2)求线段DE长度的最大值;
(3)①点P移动是否存在某个时刻,使由O、D、E、C这样的四个点为顶点的四边形为平行四边形?②点P移动是否存在某个时刻,△CDE与△BDP相似?
如果存在,就请求出所有满足条件的点P的坐标;如果不存在,请说明理由.
A
O
P
B
C
D
E
y
x
解:
参考答案
一、选择题:(本大题共10题,每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
B
A
B
D
A
B
C
二、填空题:(本大题共5小题,每小题3分,共15分)
题号
11
12
13
14
15
答案
2.5×102
-3
4或-2
40
三、解答题:(共7题,共55分)
16、解:去分母得:6= (x+1)(x-1)- (2x-5)(x+1) ………………2分
整理得:x2-3x+2=0
解得:x1=1,x1=2 …………………2分
当x=1时,(x+1)(x-1) = 0,∴x=1是增根舍去;……………1分
当x=2时,(x+1)(x-1)≠0,
∴原方程的解为x =2 …………………1分
0
60以上
10
20
30
40
50
4
8
12
16
20
塑料袋数
(个)
家庭数
(户)
17、 频数分布表 频数分布直方图
组别
每月丢塑料袋数
频数
频率
第1组
10~19
2
0.05
第2组
20~29
4
0.10
第3组
30~39
6
0.15
第4组
40~49
10
0.25
第5组
50~59
16
0.40
第6组
60以上
2
0.05
合计
40
1.00
(1)见上图和表;……………………………4分
(2)4; ……………………………1分
(3)350 ……………………………2分
18、解:(1)画图或表略 ……………………………………………………3分
得三次全是“数字”面朝上的概率 ………………………………2分
(2)得有且仅有两次“菊花”面朝上的概率 ……………………2分
19、解:设这种商品的进价为x元 …………………………1分
据题意列方程为:0.8(1+50%)x-x=20……………………3分
解之得:x=100 ……………………2分
答:这种商品的进价为100元。 ……………………1分
20、(1)见图 ………………………………………………………2分
(2)①(6,2)、(2,0)……………………………………………2分
②2;90 …………………………………………………2分
A
B
C
O
D
x
y
③ ……………………………………………………………2分
21、(1)解:∵OA是直径,∴∠OBA=90º,则 AC=2AB. ……………………………1分
∵OA=4,OB=2,得∠OAB=30º,AB=,∠AOB=60º ………………………1分
A
O
C
B
D
P·
∴AC=2AB=……………………1分
又∵AD是⊙O的切线,
∴∠OAD=90º,
在Rt△OAD中,OA=4,∠AOB=60º
∴AD= ……………………1分
∴AC=AD
又∵∠CAD=∠OAD-∠OAB=90º-30º=60º ……………………………………1分
∴△ACD是等边三角形,∴∠ADC=60º……………………………………………1分
(2)证明:连结OC,∵OA=OC
∴∠OCB =∠OAB= …………………………………………1分
又∵△ACD是等边三角形,∴∠ACD=60º ………………………………………1分
∴∠OCD=90º,而点C在⊙O上,
∴CD是⊙O的切线. …………………………………………………1分
22、解:(1)∵OA:OB=1:3
设点A(-k,0)得点B(3k,0)
又∵抛物线的对称轴是x=1,∴1+k=3k-1(也可以列式)
得k=1
∴点A(-1,0)得点B(3,0) ………………………………………2分
∵tan∠DBP=1
∴∠OBC=45º,得OC=OB=3
∴点C的坐标为(0,3) ………………………………………1分
设抛物线的函数表达式为y=a(x+1)(x-3)
把点C的坐标代入,得a= -1
∴抛物线的函数表达式为y= -x2+2x+3 ………………………………………1分
(2)由点B(3,0)和C(0,3)
得直线BC的函数解析式是y=-x+3 ………………………………………1分
设P点的横坐标为x(0
查看更多