辽阳市中考数学试题及答案

辽阳市中考数学试题及答案

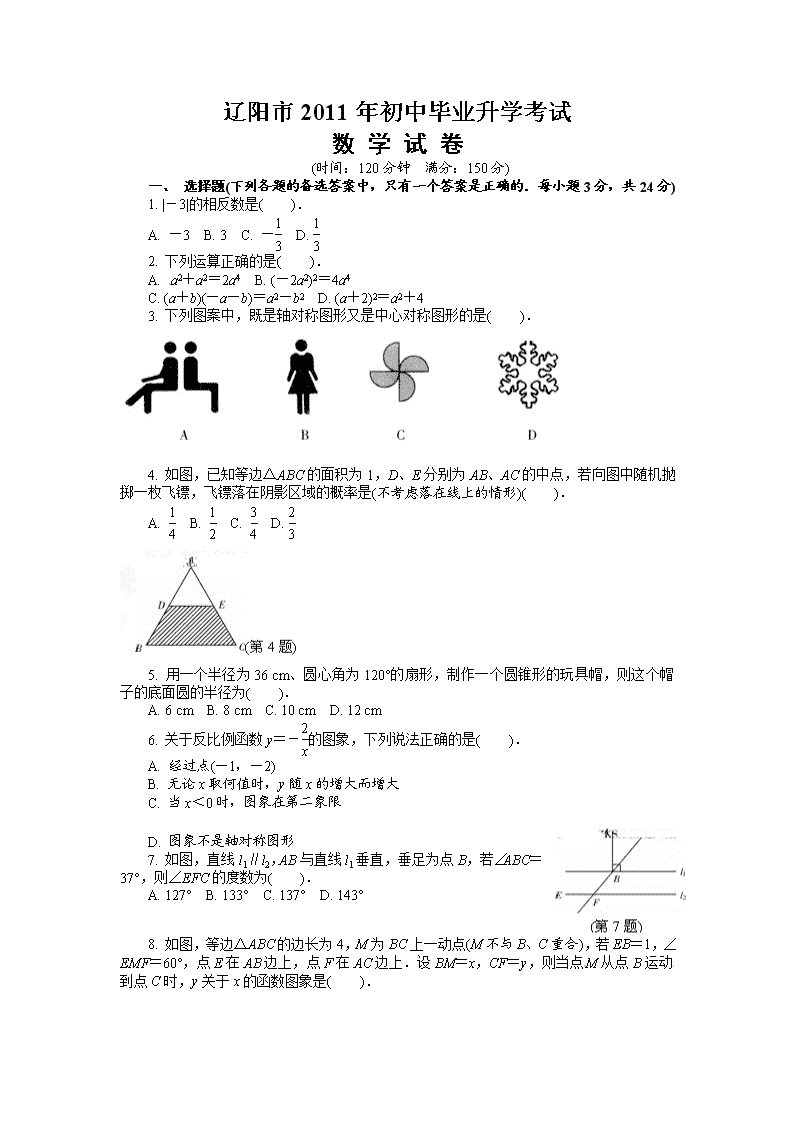
辽阳市2011年初中毕业升学考试 数 学 试 卷 ‎(时间：120分钟　满分：150分)‎ 一、 选择题(下列各题的备选答案中，只有一个答案是正确的．每小题3分，共24分)‎ ‎1. |－3|的相反数是(　　)．‎ A. －3 B. 3 C. － D. ‎2. 下列运算正确的是(　　)．‎ A. a2＋a2＝2a4 B. (－2a2)2＝4a4‎ C. (a＋b)(－a－b)＝a2－b2 D. (a＋2)2＝a2＋4‎ ‎3. 下列图案中，既是轴对称图形又是中心对称图形的是(　　)．‎ ‎4. 如图，已知等边△ABC的面积为1，D、E分别为AB、AC的中点，若向图中随机抛掷一枚飞镖，飞镖落在阴影区域的概率是(不考虑落在线上的情形)(　　)．‎ A. B. C. D. ‎5. 用一个半径为36 cm、圆心角为120°的扇形，制作一个圆锥形的玩具帽，则这个帽子的底面圆的半径为(　　)．‎ A. 6 cm B. 8 cm C. 10 cm D. 12 cm ‎6. 关于反比例函数y＝－的图象，下列说法正确的是(　　)．‎ A. 经过点(－1，－2)‎ B. 无论x取何值时，y随x的增大而增大 C. 当x＜0时，图象在第二象限 D. 图象不是轴对称图形 ‎7. 如图，直线l1∥l2，AB与直线l1垂直，垂足为点B，若∠ABC＝37°，则∠EFC的度数为(　　)．‎ A. 127° B. 133° C. 137° D. 143°‎ ‎8. 如图，等边△ABC的边长为4，M为BC上一动点(M不与B、C重合)，若EB＝1，∠EMF＝60°，点E在AB边上，点F在AC边上．设BM＝x，CF＝y，则当点M从点B运动到点C时，y关于x的函数图象是(　　)．‎ 二、 填空题(每小题3分，共24分)‎ ‎9. 函数y＝的自变量x的取值范围是________．‎ ‎10. 据统计2011年高考的报名人数约为9 600 000人，用科学记数法表示9 600 000为________．‎ ‎11. 高6m的旗杆在水平地面上的影子长4m，同一时刻附近有一建筑物的影子长20米，则该建筑物的高为________．‎ ‎12. 不等式组的解集为________．‎ ‎13. 在某校九年级安全疏散演习中，各班疏散的时间分别是3分钟，2分40秒，3分20秒，3分30秒，2分45秒，这次演习中，疏散时间的极差为________秒．‎ ‎14. 如图，AB为⊙O直径，CD⊥AB，∠BDC＝35°，则∠CAD＝________.‎ ‎(第14题)‎ ‎　　(第15题)‎ ‎　　(第16题)‎ ‎15. 如图，已知菱形ABCD的边长为2，∠BAD＝60°，若DE⊥AB，垂足为点E，则DE的长为________．‎ ‎16. 如图，在正六边形ABCDEF的内部，以AB为边作正方形ABMN，连接MC，则∠BCM的度数为________．‎ 三、 解答题(每题8分，共16分)‎ ‎17. 计算：0.25×－2＋(3.14－π)0－2sin60°.‎ ‎18. 先化简，再求值：÷，其中a＝.‎ 四、 解答题(每题10分，共20分)‎ ‎19. 为庆祝建党90周年，某中学开展了“红诗咏诵”活动，九年一班为推选学生参加此项活动，在班级内举行一次选拔赛，成绩分为A、B、C、D四个等级，并将收集的数据绘制了两幅不完整的统计图．请你根据图中所给出的信息，解答下列各题：‎ ‎(1)求九年一班共有多少人；‎ ‎(2)补全折线统计图；‎ ‎(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________；‎ ‎(4)若等级A为优秀，求该班的优秀率．‎ ‎[来源:Z*xx*k.Com]‎ ‎20. 随着家庭轿车拥有量逐年增加，渴望学习开车的人也越来越多．据统计，某驾校2008年底报名人数为3 200人，截止到2010年底报名人数已达到5 000人．‎ ‎(1)若该驾校2008年底到2010年底报名人数的年平均增长率均相同，求该驾校的年平均增长率．‎ ‎(2)若该驾校共有10名教练，预计在2011年底每个教练平均需要教授多少人？‎ 五、 解答题(每题10分，共20分)‎ ‎21. 有两个可以自由转动的转盘A、B，转盘A被分成3等份；转盘B被分成4等份，数字标注如图所示．有人设计了一个游戏，其规则如下：甲、乙两人同时转动两个转盘，转盘停止后，指针各指向一个数字，将转得的数字相乘，如果积为偶数，则甲胜；如果积为奇数，则乙胜．(若指针落在分格线上，则无效，需重新转动转盘)‎ ‎(1)你认为这个游戏公平吗？请你用所学的数学知识说明理由；‎ ‎(2)如果不公平，请你修改游戏规则，使游戏公平．‎ ‎(第21题)‎ ‎[来源:学科网ZXXK]‎ ‎22. 如图，在城市改造中，市政府欲在一条人工河上架一座桥，河的两岸PQ与MN平行，河岸MN上有A、B两个相距50米的凉亭，小亮在河对岸D处测得∠ADP＝60°，然后沿河岸走了110米到达C处，测得∠BCP＝30°，求这条河的宽．(结果保留根号)‎ ‎(第22题)‎ 六、 解答题(每题10分，共20分)‎ ‎23. 如图，⊙O经过点B、D、E，BD是⊙O的直径，∠C＝90°，BE平分∠ABC.‎ ‎(1)试说明直线AC是⊙O的切线；‎ ‎(2)当AE＝4，AD＝2时，求⊙O的半径及BC的长．‎ ‎(第23题)‎ ‎24. 甲、乙两名自行车爱好者准备在一段长为3 500米的笔直公路上进行比赛，比赛开始时乙在起点，甲在乙的前面．他们同时出发，匀速前进，已知甲的速度为12米/秒，设甲、乙两人之间的距离为s(米)，比赛时间为t(秒)，图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系．根据图中信息，回答下列问题：‎ ‎(1)乙的速度为________米/秒；‎ ‎(2)当乙追上甲时，求乙距起点多少米．‎ ‎(3)求线段BC所在直线的函数关系式．‎ ‎(第24题)‎ 七、 解答题(本题12分)‎ ‎25. 已知直角梯形ABCD，AB∥CD，∠C＝90°，AB＝BC＝CD，E为CD的中点．‎ ‎(1)如图(1)当点M在线段DE上时，以AM为腰作等腰直角三角形AMN，判断NE与MB的位置关系和数量关系，请直接写出你的结论；‎ ‎(2)如图(2)当点M在线段EC上时，其他条件不变，(1)中的结论是否成立？请说明理由．‎ ‎(1)‎ ‎　(2)‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　‎ 八、 解答题(本题14分)‎ ‎26. 如图，已知Rt△ABO，∠BAO＝90°，以点O为坐标原点，OA所在直线为y轴，建立平面直角坐标系，AO＝3，∠AOB＝30°，将Rt△ABO沿OB翻折后，点A落在第一象限内的点D处．‎ ‎(1)求D点坐标；‎ ‎(2)若抛物线y＝ax2＋bx＋3(a≠0)经过B、D两点，求此抛物线的表达式；‎ ‎(3)若抛物线的顶点为E，它的对称轴与OB交于点F，点P为射线OB上一动点，过点P作y轴的平行线，交抛物线于点M.是否存在点P，使得以E、F、M、P为顶点的四边形为等腰梯形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．参考公式：抛物线y＝ax2＋bx＋c(a≠0)的顶点坐标是.‎ ‎(第26题)‎ 辽阳市2011年初中毕业升学考试 ‎1. A　2. B　3. D　4. C　5. D　6. C　7. A　8. B ‎9. x≥3　10. 9.6×106　11. 30米[来源:学科网ZXXK]‎ ‎12. ≤x＜5　13. 50　14. 70°　15. 　16. 75°‎ ‎17. 原式＝×4＋1－2×(4分)‎ ‎＝2－.(8分)‎ ‎18. 原式＝·(3分)‎ ‎＝.(6分)‎ 当a＝时，原式＝＝.(8分)‎ ‎19. (1)30÷50%＝60(人)‎ ‎∴　九年一班共有60人．(2分)‎ ‎(2)等级为“C”的人数为60×15%＝9(人)．‎ 等级为“D”的人数为60－3－30－9＝18(人)．(4分)‎ 补全折线统计图如下．(6分)‎ ‎(第19题)‎ ‎(3)108°.(8分)‎ ‎(4)×100%＝5%.‎ ‎∴　该班的优秀率为5%.(10分)‎ ‎20. (1)设该驾校的年平均增长率是x.(1分)‎ 由题意，得3 200(1＋x)2＝5 000.(5分)‎ 解得x1＝，x2＝－(不合实际，舍去)．‎ ‎∴　该驾校的年平均增长率是25%.(7分)‎ ‎(2)5 000×(1＋25%)÷10＝625(个)．‎ ‎∴　预计2011年每个教练平均需要教授625个学员．(10分)‎ ‎21. (1)这个游戏不公平．(1分)‎ 列表如下：‎ A B ‎－1‎ ‎2‎ ‎－3‎ ‎4‎ ‎1‎ ‎(1，－1)‎ ‎(1,2)‎ ‎(1，－3)‎ ‎(1,4)‎ ‎－2‎ ‎(－2，－1)‎ ‎(－2,2)‎ ‎(－2，－3)‎ ‎(－2,4)‎ ‎3‎ ‎(3，－1)‎ ‎(3,2)‎ ‎(3，－3)‎ ‎(3,4)‎ 根据列表，共有12种可能的结果，并且每种结果出现的可能性相同，其中两数乘积为偶数的有8种，两数乘积为奇数的有4种．(5分)‎ ‎∴　P(甲胜)＝＝，P(乙胜)＝＝.‎ ‎∵　P(甲胜)＞P(乙胜)，‎ ‎∴　这个游戏不公平．(8分)‎ ‎(2)答案不唯一，只要合理即可．‎ 如：如果两数的乘积是偶数得1分，是奇数得2分等．(10分)‎ ‎22. 作AE⊥PQ于E，CF⊥MN于F.(1分)‎ ‎(第22题)‎ ‎∵　PQ∥MN，‎ ‎∴　四边形AECF为矩形．‎ ‎∴　EC＝AF，AE＝CF.(2分)‎ 设这条河宽为x米，‎ ‎∴　AE＝CF＝x.‎ 在Rt△AED中，‎ ‎∵　∠ADP＝60°，‎ ‎∴　ED＝＝＝x.(4分)‎ ‎∵　PQ∥MN，‎ ‎∴　∠CBF＝∠BCP＝30°.‎ ‎∴　在Rt△BCF中，‎ BF＝＝＝x.(6分)‎ ‎∵　EC＝ED＋CD，AF＝AB＋BF，‎ ‎∴　x＋110＝50＋x.‎ 解得x＝30.‎ ‎∴　这条河的宽为30米．(10分)‎ ‎23. (1)连接OE.[来源:学科网ZXXK]‎ ‎(第23题)‎ ‎∵　BE是∠ABC的平分线，‎ ‎∴　∠1＝∠2.‎ ‎∵　OE＝OB，‎ ‎∴　∠1＝∠3.‎ ‎∴　∠2＝∠3.‎ ‎∴　OE∥AC.‎ 又　∠C＝90°，‎ ‎∴　∠AEO＝90°.[来源:学科网]‎ ‎∴　AC是⊙O的切线．(6分)‎ ‎(2)设⊙O的半径为r，在Rt△AEO中，由勾股定理可得OA2＝OE2＋AE2.‎ ‎∵　AE＝4，AD＝2，‎ ‎∴　(2＋r)2＝r2＋42.‎ ‎∴　r＝3.‎ ‎∵　OE∥AC，‎ ‎∴　＝.‎ ‎∴　＝.‎ ‎∴　BC＝.(10分)‎ ‎24. (1)14.(2分)‎ ‎(2)由图象可知乙用了150秒追上甲，‎ ‎14×150＝2 100(米)．‎ ‎∴　当乙追上甲时，乙距起点2 100米．(5分)‎ ‎(第24题)‎ ‎(3)乙从出发到终点的时间为 ‎150＋＝250(秒)．(6分)‎ 此时甲、乙的距离为 ‎(250－150)(14－12)＝200(米)．(7分)‎ ‎∴　C(250,200)．‎ 又　B(150,0)，‎ 设BC所在直线的函数关系式为s＝kt＋b.‎ 将B、C两点代入，得(8分)‎ 解得 ‎∴　BC所在直线的函数关系式为 s＝2t－300.(10分)‎ ‎25. (1)NE＝MB且NE⊥MB.(2分)‎ ‎(2)成立．(3分)‎ 理由：连接AE.‎ ‎(第25题)‎ ‎∵　E为CD中点，AB＝BC＝CD，‎ ‎∴　AB＝EC.‎ 又　AB∥CD，‎ 即　AB∥CE.‎ ‎∴　四边形ABCE为平行四边形．‎ ‎∵　∠C＝90°，‎ ‎∴　四边形ABCE为矩形．‎ 又　AB＝BC，‎ ‎∴　四边形ABCE为正方形．‎ ‎∴　AE＝AB.‎ ‎∵　等腰直角三角形AMN中，‎ ‎∴　AN＝AM，∠NAM＝90°.‎ ‎∴　∠1＋∠2＝90°.‎ 又　∠2＋∠3＝90°，‎ ‎∴　∠1＝∠3.‎ ‎∴　△NAE≌△MAB.‎ ‎∴　NE＝MB.(9分)‎ 延长NE、BM交于点F.‎ 由△NAE≌△MAB可得，‎ ‎∠AEN＝∠ABM.‎ ‎∴　∠4＝∠6.‎ ‎∵　∠5＝∠6，‎ ‎∴　∠4＝∠5.‎ 又　∠EMF＝∠BMC，‎ ‎∴　∠EFB＝∠C＝90°.‎ ‎∴　BM⊥NE.(12分)‎ ‎26. (1)过点D作DC⊥x轴于点C，如图(1)．(1分)‎ ‎(第26题(1))‎ 由翻折可知：DO＝AO＝3，‎ ‎∠AOB＝∠BOD＝30°，‎ ‎∴　∠DOC＝30°.‎ 在Rt△COD中，‎ OC＝OD·cos30°＝3×＝，‎ CD＝OD·sin30°＝3×＝，‎ ‎∴　D.(4分)‎ ‎(2)在Rt△AOB中，‎ AB＝AO·tan30°＝3×＝，‎ ‎∴　B(，3)．‎ ‎∵　抛物线y＝ax2＋bx＋c(a≠0)经过B(，3)，D两点，‎ ‎∴　 解得 ‎∴　此抛物线表达式为y＝－x2＋x＋3.(8分)‎ ‎(3)存在符合条件的点P，设P(x，y)，‎ 作EH⊥PM于点H，FG⊥PM于点G，如图(2)．‎ ‎(第26题(2))‎ ‎∵　E为抛物线y＝－x2＋x＋3的顶点，‎ ‎∴　E.(10分)‎ 设OB所在直线的表达式为y＝kx，‎ 将点B(，3)代入，得k＝，‎ ‎∴　y＝x.‎ ‎∵　P在射线OB上，‎ ‎∴　P(x，x)，F.‎ 则H，G.‎ ‎∵　M在抛物线上，M.‎ 要使四边形EFMP为等腰梯形，只需PH＝GM.‎ x－＝－，(12分)‎ 即　－x2＋x＋3＋x＝5.‎ 解得x1＝2，x2＝.‎ ‎∴　P1点坐标为(2，6)，P2点坐标为.‎