上海市中考数学试卷及答案

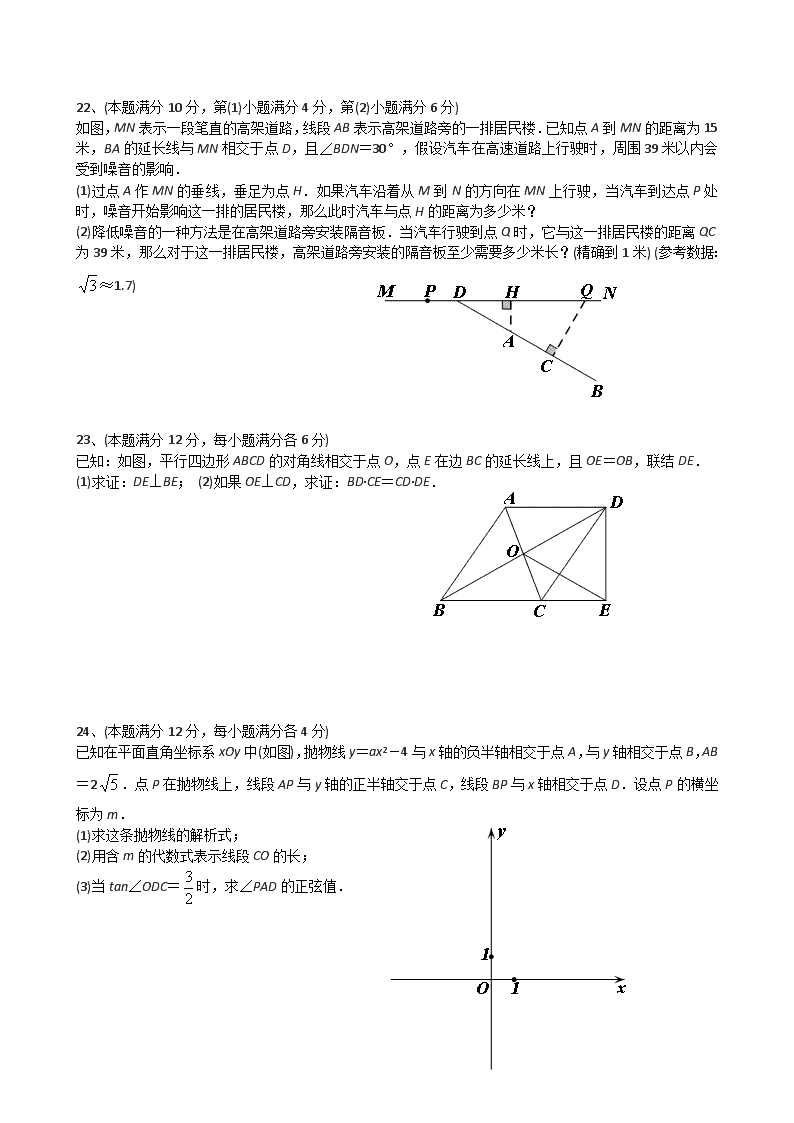
上海市中考数学试卷及答案

‎2015年上海市初中毕业统一学业考试数学试卷 一、选择题：(每题4分，共24分)‎ ‎1、下列实数中，是有理数的为………………………………………………………………（ ）‎ A、； B、； C、π； D、0．‎ ‎2、当a＞0时，下列关于幂的运算正确的是………………………………………………（ ）‎ A、a0＝1； B、a－1＝－a； C、(－a)2＝－a2； D、．‎ ‎3、下列y关于x的函数中，是正比例函数的为…………………………………………（ ）‎ A、y＝x2； B、y＝； C、y＝； D、y＝．‎ ‎4、如果一个正多边形的中心角为72°，那么这个正多边形的边数是……………………（ ）‎ A、4； B、5； C、6； D、7．‎ ‎5、下列各统计量中，表示一组数据波动程度的量是……………………………………（ ）‎ A、平均数； B、众数； C、方差； D、频率．‎ ‎6、如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是………………………………………………（ ）‎ A、AD＝BD； B、OD＝CD；‎ C、∠CAD＝∠CBD； D、∠OCA＝∠OCB．‎ 二、填空题：(每题4分，共48分)‎ ‎7、计算：_______．‎ ‎8、方程的解是_______________．‎ ‎9、如果分式有意义，那么x的取值范围是____________．‎ ‎10、如果关于x的一元二次方程x2＋4x－m＝0没有实数根，那么m的取值范围是________．‎ ‎11、同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y＝x＋32．如果某一温度的摄氏度数是25℃，那么它的华氏度数是________℉．‎ ‎12、如果将抛物线y＝x2＋2x－1向上平移，使它经过点A(0，3)，那么所得新抛物线的表达式是_______________．‎ ‎13、某校学生会提倡双休日到养老院参加服务活动，首次活动需要7位同学参加，现有包括小杰在内的50位同学报名，因此学生会将从这50位同学中随机抽取7位，小杰被抽到参加首次活动的概率是__________．‎ ‎14、已知某校学生“科技创新社团”成员的年龄与人数情况如下表所示：‎ 年龄(岁)‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 人数 ‎5‎ ‎5‎ ‎16‎ ‎15‎ ‎12‎ 那么“科技创新社团”成员年龄的中位数是_______岁．‎ ‎15、如图，已知在△ABC中，D、E分别是边AB、边AC的中点，，，那么向量用向量、表示为______________．‎ ‎16、已知E是正方形ABCD的对角线AC上一点，AE＝AD，过点E作AC 的垂线，交边CD于点F，那么∠FAD＝________度．‎ ‎17、在矩形ABCD中，AB＝5，BC＝12，点A在⊙B上．如果⊙D与⊙B相交，且点B在⊙D内，那么⊙D的半径长可以等于___________．(只需写出一个符合要求的数)‎ ‎18、已知在△ABC中，AB＝AC＝8，∠BAC＝30°．将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处．延长线段AD，交原△ABC的边BC的延长线于点E，那么线段DE的长等于___________．‎ 三、解答题 ‎19、(本题满分10分)先化简，再求值：，其中．‎ ‎20、(本题满分10分)‎ 解不等式组：，并把解集在数轴上表示出来．‎ ‎21、(本题满分10分，第(1)小题满分4分，第(2)小题满分6分)‎ 已知：如图，在平面直角坐标系xOy中，正比例函数y＝x的图像经过点A，点A的纵坐标为4，反比例函数y＝的图像也经过点A，第一象限内的点B在这个反比例函数的图像上，过点B作BC∥x轴，交y轴于点C，且AC＝AB．‎ 求：(1)这个反比例函数的解析式； (2)直线AB的表达式．‎ ‎22、(本题满分10分，第(1)小题满分4分，第(2)小题满分6分)‎ 如图，MN表示一段笔直的高架道路，线段AB表示高架道路旁的一排居民楼．已知点A到MN的距离为15米，BA的延长线与MN相交于点D，且∠BDN＝30°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．‎ ‎(1)过点A作MN的垂线，垂足为点H．如果汽车沿着从M到N的方向在MN上行驶，当汽车到达点P处时，噪音开始影响这一排的居民楼，那么此时汽车与点H的距离为多少米？‎ ‎(2)降低噪音的一种方法是在高架道路旁安装隔音板．当汽车行驶到点Q时，它与这一排居民楼的距离QC为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？(精确到1米) (参考数据：≈1.7)‎ ‎23、(本题满分12分，每小题满分各6分)‎ 已知：如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE＝OB，联结DE．‎ ‎(1)求证：DE⊥BE； (2)如果OE⊥CD，求证：BD·CE＝CD·DE．‎ ‎24、(本题满分12分，每小题满分各4分)‎ 已知在平面直角坐标系xOy中(如图)，抛物线y＝ax2－4与x轴的负半轴相交于点A，与y轴相交于点B，AB＝2．点P在抛物线上，线段AP与y轴的正半轴交于点C，线段BP与x轴相交于点D．设点P的横坐标为m．‎ ‎(1)求这条抛物线的解析式；‎ ‎(2)用含m的代数式表示线段CO的长；‎ ‎(3)当tan∠ODC＝时，求∠PAD的正弦值．‎ ‎25、(本题满分14分，第(1)小题满分4分，第(2)小题满分5分，第(3)小题满分5分)‎ 已知：如图，AB是半圆O的直径，弦CD∥AB，动点P、Q分别在线段OC、CD上，且DQ＝OP，AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C、D不重合)，AB＝20，cos∠AOC＝．设OP＝x，△CPF的面积为y．‎ ‎(1)求证：AP＝OQ；‎ ‎(2)求y关于x的函数关系式，并写出它的定义域；‎ ‎(3)当△OPE是直角三角形时，求线段OP的长．‎ 新课 标第 一 网 ‎