中考数学模拟试卷含解析10

中考数学模拟试卷含解析10

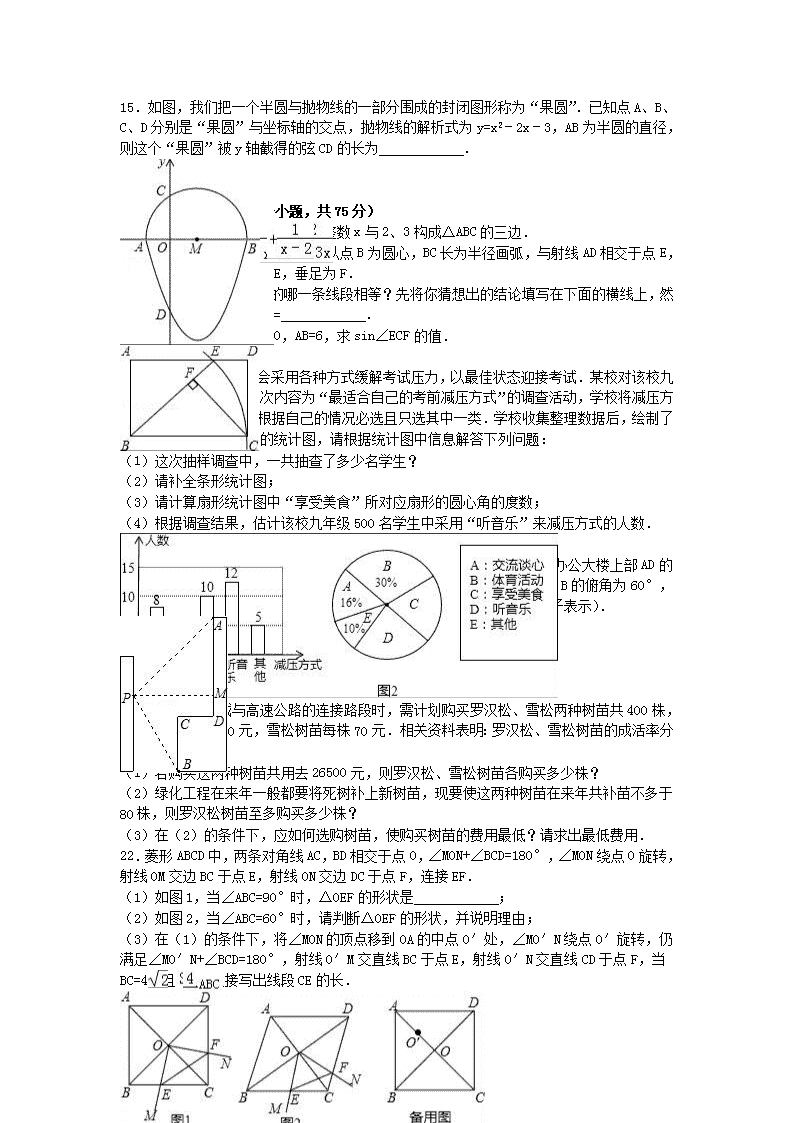
‎2016年河南省信阳市中考数学模拟试卷 一、选择题(每小题3分，共24分)‎ ‎1．﹣的倒数是（　　）‎ A．﹣7 B．7 C． D．﹣‎ ‎2．如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（　　）‎ A．22.5° B．36° C．45° D．90°‎ ‎3．下面平面图形中能围成三棱柱的是（　　）‎ A． B． C． D．‎ ‎4．在某校“我的中国梦”演讲比赛中，有9名学生参加比赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（　　）‎ A．众数 B．方差 C．平均数 D．中位数 ‎5．如果关于x的一元二次方程kx2﹣6x+9=0有两个不相等的实数根，那么k的取值范围是（　　）‎ A．k＜1 B．k≠0 C．k＜1且k≠0 D．k＞1‎ ‎6．不等式组的解集在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎7．某工厂生产一种零件，计划在20天内完成，若每天多生产4个，则15天完成且还多生产10个．设原计划每天生产x个，根据题意可列分式方程为（　　）‎ A． B． C． D．‎ ‎8．如图，在平面直角坐标系中，边长为1的正方形ABCD中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（每小题3分，共21分）‎ ‎9．分解因式：2x2﹣8=　　　　　　．‎ ‎10．计算：（）﹣1﹣|﹣2+tan45°|=　　　　　　．‎ ‎11．在六张卡片上分别写有π，，1.5，﹣3，0，六个数，从中任意抽取一张，卡片上的数为无理数的概率是　　　　　　．‎ ‎12．如图，抛物线y1=a（x+2）2+m过原点，与抛物线y2=（x﹣3）2+n交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．下列结论：①两条抛物线的对称轴距离为5；②x=0时，y2=5；③当x＞3时，y1﹣y2＞0；④y轴是线段BC的中垂线．正确结论是　　　　　　（填写正确结论的序号）．‎ ‎13．如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC=60°，弦AD平分∠BAC，若AD=6，那么AC=　　　　　　．‎ ‎14．如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是　　　　　　（结果保留π）．‎ ‎15．如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x2﹣2x﹣3，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为　　　　　　．‎ ‎　‎ 三、解答题（本题有8个小题，共75分）‎ ‎16．先化简，再求值： +1，其中整数x与2、3构成△ABC的三边．‎ ‎17．如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．‎ ‎（1）线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．结论：BF=　　　　　　．‎ ‎（2）连结CE，如果BC=10，AB=6，求sin∠ECF的值．‎ ‎18．考试前，同学们总会采用各种方式缓解考试压力，以最佳状态迎接考试．某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动，学校将减压方式分为五类，同学们可根据自己的情况必选且只选其中一类．学校收集整理数据后，绘制了图1和图2两幅不完整的统计图，请根据统计图中信息解答下列问题：‎ ‎（1）这次抽样调查中，一共抽查了多少名学生？‎ ‎（2）请补全条形统计图；‎ ‎（3）请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数；‎ ‎（4）根据调查结果，估计该校九年级500名学生中采用“听音乐”来减压方式的人数．‎ ‎19．小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD=10米．求点P到AD的距离（用含根号的式子表示）．‎ ‎20．已知关于x的一元二次方程ax2﹣（a+2）x+2=0．‎ ‎（1）不解方程，判别方程的根的情况；‎ ‎（2）方程有两个不相等的正整数根时，求整数a的值．‎ ‎21．在绿化某县城与高速公路的连接路段时，需计划购买罗汉松、雪松两种树苗共400株，罗汉松树苗每株60元，雪松树苗每株70元．相关资料表明：罗汉松、雪松树苗的成活率分别为70%、90%．‎ ‎（1）若购买这两种树苗共用去26500元，则罗汉松、雪松树苗各购买多少株？‎ ‎（2）绿化工程在来年一般都要将死树补上新树苗，现要使这两种树苗在来年共补苗不多于80株，则罗汉松树苗至多购买多少株？‎ ‎（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？请求出最低费用．‎ ‎22．菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．‎ ‎（1）如图1，当∠ABC=90°时，△OEF的形状是　　　　　　；‎ ‎（2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；‎ ‎（3）在（1）的条件下，将∠MON的顶点移到OA的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且=时，直接写出线段CE的长．‎ ‎23．如图，已知二次函数y=ax2+bx+8（a≠0）的图象与x轴相交于点A（﹣2，0），B，与y轴相交于点C，tan∠ABC=2．‎ ‎（1）抛物线的解析式为　　　　　　，其顶点D的坐标为　　　　　　；‎ ‎（2）设置点CD交x轴于点E，过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点，试探究：抛物线最多可以向上平移多少个单位长度？‎ ‎（3）在线段OB的处置平分线上是否存在点P，是的经过点P的直线PM垂直于直线CD，且与直线OP的夹角为75°，若存在直接写出点P的坐标；若不存在，请说明理由．‎ ‎　‎ ‎2016年河南省信阳市中考数学模拟试卷 参考答案与试题解析 ‎　‎ 一、选择题(每小题3分，共24分)‎ ‎1．﹣的倒数是（　　）‎ A．﹣7 B．7 C． D．﹣‎ ‎【考点】倒数．‎ ‎【分析】直接根据倒数的定义求解．‎ ‎【解答】解：﹣的倒数是﹣7，‎ 故选A．‎ ‎　‎ ‎2．如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（　　）‎ A．22.5° B．36° C．45° D．90°‎ ‎【考点】平行线的性质．‎ ‎【分析】根据等腰直角三角形定义可知∠B=45°，再由平行线性质得出∠1与∠B相等，由此得出∠1也是45°．‎ ‎【解答】解：∵△ABC为等腰直角三角形，∠BAC=90°，‎ ‎∴∠B=45°，‎ ‎∵a∥b，‎ ‎∴∠1=∠B=45°，‎ 故选C．‎ ‎　‎ ‎3．下面平面图形中能围成三棱柱的是（　　）‎ A． B． C． D．‎ ‎【考点】展开图折叠成几何体．‎ ‎【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．‎ ‎【解答】解：A、能围成三棱柱，故选项正确；‎ B、折叠后有两个面重合，不能围成三棱柱，故选项错误；‎ C、不能围成三棱柱，故选项错误；‎ D、折叠后有两个侧面重合，不能围成三棱柱，故选项错误．‎ 故选：A．‎ ‎　‎ ‎4．在某校“我的中国梦”演讲比赛中，有9名学生参加比赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（　　）‎ A．众数 B．方差 C．平均数 D．中位数 ‎【考点】统计量的选择．‎ ‎【分析】9人成绩的中位数是第5名的成绩．参赛选手要想知道自己是否能进入前5名，只需要了解自己的成绩以及全部成绩的中位数，比较即可．‎ ‎【解答】解：由于总共有9个人，且他们的分数互不相同，第5的成绩是中位数，要判断是否进入前5名，故应知道中位数的多少．‎ 故选：D．‎ ‎　‎ ‎5．如果关于x的一元二次方程kx2﹣6x+9=0有两个不相等的实数根，那么k的取值范围是（　　）‎ A．k＜1 B．k≠0 C．k＜1且k≠0 D．k＞1‎ ‎【考点】根的判别式；一元二次方程的定义．‎ ‎【分析】方程有两个不相等的实数根，则△＞0，由此建立关于k的不等式，然后就可以求出k的取值范围．‎ ‎【解答】解：由题意知：k≠0，△=36﹣36k＞0，‎ ‎∴k＜1且k≠0．‎ 故选：C．‎ ‎　‎ ‎6．不等式组的解集在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎【考点】在数轴上表示不等式的解集；解一元一次不等式组．‎ ‎【分析】先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．‎ ‎【解答】解：由3x﹣1≤2（x+1），得x≤3，‎ 由＞，得x＞﹣2，‎ 不等式组的解集是﹣2＜x≤3，‎ 故选：B．‎ ‎　‎ ‎7．某工厂生产一种零件，计划在20天内完成，若每天多生产4个，则15天完成且还多生产10个．设原计划每天生产x个，根据题意可列分式方程为（　　）‎ A． B． C． D．‎ ‎【考点】由实际问题抽象出分式方程．‎ ‎【分析】设原计划每天生产x个，则实际每天生产（x+4）个，根据题意可得等量关系：（原计划20天生产的零件个数+10个）÷实际每天生产的零件个数=15天，根据等量关系列出方程即可．‎ ‎【解答】解：设原计划每天生产x个，则实际每天生产（x+4）个，根据题意得：‎ ‎=15，‎ 故选：A．‎ ‎　‎ ‎8．如图，在平面直角坐标系中，边长为1的正方形ABCD中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（　　）‎ A． B． C． D．‎ ‎【考点】动点问题的函数图象．‎ ‎【分析】将动点P的运动过程划分为PD、DC、CB、BA、AP共5个阶段，分别进行分析，最后得出结论．‎ ‎【解答】解：动点P运动过程中：‎ ‎①当0≤s≤时，动点P在线段PD上运动，此时y=2保持不变；‎ ‎②当＜s≤时，动点P在线段DC上运动，此时y由2到1逐渐减少；‎ ‎③当＜s≤时，动点P在线段CB上运动，此时y=1保持不变；‎ ‎④当＜s≤时，动点P在线段BA上运动，此时y由1到2逐渐增大；‎ ‎⑤当＜s≤4时，动点P在线段AP上运动，此时y=2保持不变．‎ 结合函数图象，只有D选项符合要求．‎ 故选：D．‎ ‎　‎ 二、填空题（每小题3分，共21分）‎ ‎9．分解因式：2x2﹣8=　2（x+2）（x﹣2）　．‎ ‎【考点】因式分解-提公因式法．‎ ‎【分析】观察原式，找到公因式2，提出即可得出答案．‎ ‎【解答】解：2x2﹣8=2（x+2）（x﹣2）．‎ ‎　‎ ‎10．计算：（）﹣1﹣|﹣2+tan45°|=　1+　．‎ ‎【考点】实数的运算；负整数指数幂；特殊角的三角函数值．‎ ‎【分析】分别进行负整数指数幂、特殊角的三角函数值、绝对值的化简等运算，然后合并．‎ ‎【解答】解：原式=3+（﹣2+）‎ ‎=1+．‎ 故答案为：1+．‎ ‎　‎ ‎11．在六张卡片上分别写有π，，1.5，﹣3，0，六个数，从中任意抽取一张，卡片上的数为无理数的概率是　　．‎ ‎【考点】概率公式；无理数．‎ ‎【分析】由π，，1.5，﹣3，0，六个数中，无理数为：π，，直接利用概率公式求解即可求得答案．‎ ‎【解答】解：∵π，，1.5，﹣3，0，六个数中，无理数为：π，，‎ ‎∴从中任意抽取一张，卡片上的数为无理数的概率是： =．‎ 故答案为：．‎ ‎　‎ ‎12．如图，抛物线y1=a（x+2）2+m过原点，与抛物线y2=（x﹣3）2+n交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．下列结论：①两条抛物线的对称轴距离为5；②x=0时，y2=5；③当x＞3时，y1﹣y2＞0；④y轴是线段BC的中垂线．正确结论是　①③④　（填写正确结论的序号）．‎ ‎【考点】二次函数的性质；二次函数图象上点的坐标特征．‎ ‎【分析】把点A坐标与原点坐标代入y1，求出a、m的值，即可得到函数解析式，把点A坐标代入y2，求出n的值，即可得到函数解析式，再判定①；令x=0，求出y2与y轴的交点，判定②；令y=3，求出A、B、C的横坐标，然后求出AB、AC的长，判定④．‎ ‎【解答】解：∵抛物线y1=a（x+2）2+m与抛物线y2=（x﹣3）2+n的对称轴分别为x=﹣2，x=3，‎ ‎∴两条抛物线的对称轴距离为5，故①正确；‎ ‎∵y1=a（x+2）2+m经过点A（1，3）与原点，‎ ‎∴，‎ 解得，‎ ‎∴y1=（x+2）2﹣，‎ ‎∵y2=（x﹣3）2+n经过点A（1，3），‎ ‎∴（1﹣3）2+n=3，‎ 解得n=1，‎ ‎∴y2=（x﹣3）2+1，‎ 当x=0时，y=（0﹣3）2+1=5.5，故②错误；‎ 由图象得，当x＞1时，y1＞y2，故③正确；‎ ‎∵过点A作x轴的平行线，分别交两条抛物线于点B，C，‎ ‎∴令y=3，则（x+2）2﹣=3，‎ 整理得，（x+2）2=9，‎ 解得x1=﹣5，x2=1，‎ ‎∴AB=1﹣（﹣5）=6，‎ ‎∴A（1，3），B（﹣5，3）；‎ 令y=3，则（x﹣3）2+1=3，‎ 整理得，（x﹣3）2=4，‎ 解得x1=5，x2=1，‎ ‎∴C（5，3），‎ ‎∴AC=5﹣1=4，‎ ‎∴BC=10，‎ ‎∴y轴是线段BC的中垂线，故④正确．‎ 故答案为①③④．‎ ‎　‎ ‎13．如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC=60°，弦AD平分∠BAC，若AD=6，那么AC=　　．‎ ‎【考点】圆周角定理；垂径定理．‎ ‎【分析】首先连接BD，由AB是⊙O的直径，可得∠C=∠D=90°，然后由∠BAC=60°，弦AD平分∠BAC，求得∠BAD的度数，又由AD=6，求得AB的长，继而求得答案．‎ ‎【解答】解：连接BD，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠C=∠D=90°，‎ ‎∵∠BAC=60°，弦AD平分∠BAC，‎ ‎∴∠BAD=∠BAC=30°，‎ ‎∴在Rt△ABD中，AB===4，‎ ‎∴在Rt△ABC中，AC=AB•cos60°=4×=2．‎ 故答案为：2．‎ ‎　‎ ‎14．如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是　3﹣π　（结果保留π）．‎ ‎【考点】扇形面积的计算；平行四边形的性质．‎ ‎【分析】过D点作DF⊥AB于点F．可求▱ABCD和△BCE的高，观察图形可知阴影部分的面积=▱ABCD的面积﹣扇形ADE的面积﹣△BCE的面积，计算即可求解．‎ ‎【解答】解：过D点作DF⊥AB于点F．‎ ‎∵AD=2，AB=4，∠A=30°，‎ ‎∴DF=AD•sin30°=1，EB=AB﹣AE=2，‎ ‎∴阴影部分的面积：‎ ‎4×1﹣﹣2×1÷2‎ ‎=4﹣π﹣1‎ ‎=3﹣π．‎ 故答案为：3﹣π．‎ ‎　‎ ‎15．如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x2﹣2x﹣3，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为　3+　．‎ ‎【考点】二次函数综合题．‎ ‎【分析】连接AC，BC，有抛物线的解析式可求出A，B，C的坐标，进而求出AO，BO，DO的长，在直角三角形ACB中，利用射影定理可求出CO的长，进而可求出CD的长．‎ ‎【解答】解：连接AC，BC，‎ ‎∵抛物线的解析式为y=x2﹣2x﹣3，‎ ‎∴点D的坐标为（0，﹣3），‎ ‎∴OD的长为3，‎ 设y=0，则0=x2﹣2x﹣3，‎ 解得：x=﹣1或3，‎ ‎∴A（﹣1，0），B（3，0）‎ ‎∴AO=1，BO=3，‎ ‎∵AB为半圆的直径，‎ ‎∴∠ACB=90°，‎ ‎∵CO⊥AB，‎ ‎∴CO2=AO•BO=3，‎ ‎∴CO=，‎ ‎∴CD=CO+OD=3+，‎ 故答案为：3+．‎ ‎　‎ 三、解答题（本题有8个小题，共75分）‎ ‎16．先化简，再求值： +1，其中整数x与2、3构成△ABC的三边．‎ ‎【考点】分式的化简求值；三角形三边关系．‎ ‎【分析】原式第一项约分后，三项通分并利用同分母分式的加减法则计算得到最简结果，由题意确定出x的值代入计算即可求出值．‎ ‎【解答】解：原式=•++1=++1=+1=+1=，‎ ‎∵整数x与2，3构成△ABC三边，‎ ‎∴3﹣2＜x＜3+2，即1＜x＜5，即x=2，3，4，‎ 由分母x﹣2≠0，x+2≠0，x≠0，x﹣3≠0，‎ 得到x≠0，﹣2，2，3，即x=4，‎ 则原式=2．‎ ‎　‎ ‎17．如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．‎ ‎（1）线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．结论：BF=　AE　．‎ ‎（2）连结CE，如果BC=10，AB=6，求sin∠ECF的值．‎ ‎【考点】全等三角形的判定与性质；作图—复杂作图；解直角三角形．‎ ‎【分析】（1）BF=AE，理由为：由AD与BC平行得到一对内错角相等，再由一对直角相等，且BE=CB，利用AAS得到三角形AEB与三角形FBC全等，利用全等三角形对应角相等即可得证；‎ ‎（2）连接CE，如图所示，由（1）的全等三角形得到对应边相等，进而求出EF与EC的长，利用锐角三角函数定义求出sin∠ECF的值即可．‎ ‎【解答】解：（1）BF=AE，理由为：‎ ‎∵CF⊥BE，‎ ‎∴∠A=∠BFC=90°，‎ ‎∵AD∥BC，‎ ‎∴∠AEB=∠FBC，‎ 在△AEB和△FBC中，‎ ‎，‎ ‎∴△AEB≌△FBC（AAS），‎ ‎∴BF=AE；‎ 故答案为：AE；‎ ‎（2）连接AE，如图所示，‎ ‎∵△AEB≌△FBC，‎ ‎∴BF=AE，CF=AB=6，BE=BC=10，‎ 根据勾股定理得：AE=BF=8，‎ ‎∴EF=BE﹣BF=10﹣8=2，‎ 在Rt△EFC中，根据勾股定理得：EC==2，‎ 则sin∠ECF==．‎ ‎　‎ ‎18．考试前，同学们总会采用各种方式缓解考试压力，以最佳状态迎接考试．某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动，学校将减压方式分为五类，同学们可根据自己的情况必选且只选其中一类．学校收集整理数据后，绘制了图1和图2两幅不完整的统计图，请根据统计图中信息解答下列问题：‎ ‎（1）这次抽样调查中，一共抽查了多少名学生？‎ ‎（2）请补全条形统计图；‎ ‎（3）请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数；‎ ‎（4）根据调查结果，估计该校九年级500名学生中采用“听音乐”来减压方式的人数．‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）利用“流谈心”的人数除以所占的百分比计算即可得解；‎ ‎（2）用总人数乘以“体育活动”所占的百分比计算求出体育活动的人数，然后补全统计图即可；‎ ‎（3）用360°乘以“享受美食”所占的百分比计算即可得解；‎ ‎（4）用总人数乘以“听音乐”所占的百分比计算即可得解．‎ ‎【解答】解：（1）一共抽查的学生：8÷16%=50人；‎ ‎（2）参加“体育活动”的人数为：50×30%=15，‎ 补全统计图如图所示：‎ ‎（3）“享受美食”所对应扇形的圆心角的度数为：360°×=72°；‎ ‎（4）该校九年级500名学生中采用“听音乐”来减压方式的人数为：500×=120人．‎ ‎　‎ ‎19．小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD=10米．求点P到AD的距离（用含根号的式子表示）．‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】连接PA、PB，过点P作PM⊥AD于点M；延长BC，交PM于点N，将实际问题中的已知量转化为直角三角形中的有关量，设PM=x米，在Rt△PMA中，表示出AM，在Rt△PNB中，表示出BN，由AM+BN=46米列出方程求解即可．‎ ‎【解答】解：连接PA、PB，过点P作PM⊥AD于点M；延长BC，交PM于点N 则∠APM=45°，∠BPM=60°，NM=10米 设PM=x米 在Rt△PMA中，AM=PM×tan∠APM=xtan45°=x（米）‎ 在Rt△PNB中，BN=PN×tan∠BPM=（x﹣10）tan60°=（x﹣10）（米）‎ 由AM+BN=46米，得x+（x﹣10）=46‎ 解得， =18﹣8，‎ ‎∴点P到AD的距离为米．‎ ‎　‎ ‎20．已知关于x的一元二次方程ax2﹣（a+2）x+2=0．‎ ‎（1）不解方程，判别方程的根的情况；‎ ‎（2）方程有两个不相等的正整数根时，求整数a的值．‎ ‎【考点】根的判别式．‎ ‎【分析】（1）由一元二次方程的定义可得出a≠0，再利用根的判别式△=b2﹣4ac，套入数据即可得出△=（a﹣2）2≥0，由此即可得出结论；‎ ‎（2）结合（1）的结论可得出a≠2且a≠0，设方程的两个根分别为x1、x2，利用根与系数的关系可得出x1•x2=，再根据x1、x2均为正整数，a为整数，即可得出结论．‎ ‎【解答】解：（1）∵方程ax2﹣（a+2）x+2=0是关于x的一元二次方程，‎ ‎∴a≠0．‎ ‎∵△=（a+2）2﹣4a×2=（a﹣2）2≥0，‎ ‎∴当a=2时，方程有两个相等的实数根，当a≠2且a≠0时，方程有两个不相等的实数根．‎ ‎（2）∵方程有两个不相等的正整数根，‎ ‎∴a≠2且a≠0．‎ 设方程的两个根分别为x1、x2，‎ ‎∴x1•x2=，‎ ‎∵x1、x2均为正整数，‎ ‎∴为正整数，‎ ‎∵a为整数，a≠2且a≠0，‎ ‎∴a=1．‎ ‎　‎ ‎21．在绿化某县城与高速公路的连接路段时，需计划购买罗汉松、雪松两种树苗共400株，罗汉松树苗每株60元，雪松树苗每株70元．相关资料表明：罗汉松、雪松树苗的成活率分别为70%、90%．‎ ‎（1）若购买这两种树苗共用去26500元，则罗汉松、雪松树苗各购买多少株？‎ ‎（2）绿化工程在来年一般都要将死树补上新树苗，现要使这两种树苗在来年共补苗不多于80株，则罗汉松树苗至多购买多少株？‎ ‎（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？请求出最低费用．‎ ‎【考点】一次函数的应用；二元一次方程组的应用．‎ ‎【分析】设购买罗汉松树苗x株，雪松树苗y株，（1）根据两种树苗的株数和费用列出二元一次方程组，然后求解即可；‎ ‎（2）根据罗汉松树苗的株数表示出雪松树苗为株，然后根据成活的两种树苗数列出不等式，求解即可；‎ ‎（3）表示出两种树苗的费用数，然后根据一次函数的增减性求出费用最小值即可．‎ ‎【解答】解：（1）设购买罗汉松树苗x株，雪松树苗y株，‎ 则据题意可得，‎ 解得，‎ 答：购买罗汉松树苗150株，雪松树苗250株；‎ ‎（2）设购买罗汉松树苗x株，则购买雪松树苗株，‎ 由题意得，70%x+90%≥，‎ 解得x≤200，‎ 答：罗汉松树苗至多购买200株；‎ ‎（3）设罗汉松树苗购买x株，购买树苗的费用为W元，‎ 则有W=60x+70=﹣10x+28000，‎ 显然W是关于x的一次函数，‎ ‎∵﹣10＜0，‎ ‎∴W随x的增大而减小，‎ 故当x取最大值时，W最小，‎ ‎∵0＜x≤200，‎ ‎∴当x=200时，W取得最小值，且W最小=﹣10×200+28000=26000．‎ 答：当选购罗汉松树苗200株，雪松树苗200株时，总费用最低，为26000元．‎ ‎　‎ ‎22．菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．‎ ‎（1）如图1，当∠ABC=90°时，△OEF的形状是　等腰直角三角形　；‎ ‎（2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；‎ ‎（3）在（1）的条件下，将∠MON的顶点移到OA的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且=时，直接写出线段CE的长．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）△OEF是等腰直角三角形，只要证明△OBE≌△OCF即可．‎ ‎（2））△OEF是等边三角形，如图2所示：过点O作OG⊥BC与G，作OH⊥CD与H．先证明△OGE≌△OHF，得OE=OF，证明∠EOF=60°即可解决问题．‎ ‎（3）CE=3+3或3﹣3．见如图3中两种情形，作O′G⊥BC于G，O′H⊥CD于H，只要证明△OGE≌△OHF推出△EOF是等腰直角三角形，求出EG即可解决问题．‎ ‎【解答】解：（1）结论：△OEF是等腰直角三角形．‎ 理由：∵四边形ABCD为菱形，∠ABC=90°，‎ ‎∴四边形ABCD为正方形．‎ ‎∴OB=OC，∠OBE=∠OCN=45°，∠BOC=90°，∠BCD=90°．‎ 又∵∠MON+∠BCD=180°，‎ ‎∴∠EOF=90°．‎ ‎∴∠EOC+COF=90°．‎ ‎∵∠BOE+∠EOC=90°，‎ ‎∴∠BOE=∠COF．‎ 在△OBE和△OCF中 ‎，‎ ‎∴△OBE≌△OCF，‎ ‎∴OE=OF．‎ ‎∴△OEF为等腰直角三角形．‎ 故答案为等腰直角三角形．‎ ‎（2）结论：△OEF是等边三角形，‎ 证明：如图2所示：过点O作OG⊥BC与G，作OH⊥CD与H．‎ 过O作OG⊥BC于G，OH⊥CD于H，‎ ‎∴∠OGE=∠OGC=∠OHC=90°‎ ‎∵四边形ABCD是菱形，‎ ‎∴CA平分∠BCD，∠ABC+∠BCD=180°，‎ ‎∴OG=OH，∠BCD=180°﹣60°=120°，‎ ‎∵∠GOH+∠OGC+∠BCD+∠OHC=360°，‎ ‎∴∠GOH+∠BCD=180°，‎ ‎∵∠MON+∠BCD=180°，‎ ‎∴∠EOF=∠GOH=180°﹣∠BCD=60°，‎ ‎∴∠EOF﹣∠GOF=∠GOH﹣∠GOF，‎ ‎∴∠EOG=∠FOH，‎ 在△EOG和△FOH中，‎ ‎，‎ ‎∴△OGE≌△OHF，‎ ‎∴OE=OF，‎ ‎∵∠EOF=60°，‎ ‎∴△EOF是等边三角形．‎ ‎（3）CE=3+3或3﹣3．‎ 理由：如图3中，∵菱形ABCD中，∠ABC=90°，‎ ‎∴四边形ABCD是正方形， =，‎ 作O′G⊥BC于G，O′H⊥CD于H，‎ ‎∴∠O′GC=∠O′HC=∠GCH=90°，‎ ‎∴四边形O′GCH是矩形，‎ ‎∴O′G∥AB，O′H∥AD，‎ ‎∴===，‎ ‎∵AB=BC=CD=AD=4，‎ ‎∴O′G=O′H=3，‎ ‎∴四边形O′GCH是正方形，‎ ‎∴CG=O′G=3，∠GO′H=90°，‎ ‎∵∠MO∠′N+∠BCD=180°，∠BCD=90°，‎ ‎∴∠EO′F=90°，‎ ‎∴∠EO′F=∠GO′H=90°，‎ ‎∴∠EO′G=∠FO′H，‎ 在△EO′G和△FO′H中，‎ ‎，‎ ‎∴△EO′G≌△FO′H，‎ ‎∴O′E=O′F，‎ ‎∴△O′EF是等腰直角三角形，‎ ‎∵S△ABC=×4×4=16， =，‎ ‎∴S△OEF=36，‎ 在RT△O′EG中，EG==3，‎ ‎∴CE=EG+CG=3+3，‎ 根据对称性可知，当∠MON旋转到如图所示位置时，‎ CE′=E′G﹣CG=3﹣3．‎ 综上所述CE=3+3或3﹣3‎ ‎　‎ ‎23．如图，已知二次函数y=ax2+bx+8（a≠0）的图象与x轴相交于点A（﹣2，0），B，与y轴相交于点C，tan∠ABC=2．‎ ‎（1）抛物线的解析式为　y=﹣（x﹣1）2+9　，其顶点D的坐标为　（1，9）　；‎ ‎（2）设置点CD交x轴于点E，过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点，试探究：抛物线最多可以向上平移多少个单位长度？‎ ‎（3）在线段OB的处置平分线上是否存在点P，是的经过点P的直线PM垂直于直线CD，且与直线OP的夹角为75°，若存在直接写出点P的坐标；若不存在，请说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）根据正切函数，可得B点坐标，根据待定系数法，可得函数解析式，根据配方法，可得顶点坐标；‎ ‎（2）根据待定系数法，可得CD的解析式，根据自变量与函数值的对应关系，可得E．F点坐标，根据函数图象向上平移加，可得平移后的解析式，根据抛物线与线段有交点，可得抛物线的函数值小于E、F的纵坐标，可得答案；‎ ‎（3）根据四边形的内角和，可得∠MPN的度数，根据角的和差，可得∠OPN，根据三角函数，可得PN的长，可得P点坐标．‎ ‎【解答】解：（1）当x=0时，y=8，即C（0，8），‎ 由tan∠ABC=2，得B（4，0）．‎ 将A、B点坐标代入函数解析式，得 ‎，‎ 解得，‎ y=﹣x2+2x+8，‎ 配方，得 y=﹣（x﹣1）2+9，顶点D（1，9），‎ 故答案为：y=﹣（x﹣1）2+9，（1，9）；‎ ‎（2）设直线CD的解析式为y=kx+8，‎ 将D（1，9）代入函数解析式，‎ 得k=1，‎ 直线CD的解析式为y=x+8，‎ 当y=0时，x=﹣8，即E（﹣8，0），‎ 当x=4时，y=4+8=12，即F（4，12）．‎ 设抛物线向上平移m各单位长度（m＞0）后抛物线的解析式为y=﹣（x﹣1）2+9+m，‎ 当x=﹣8时，y=m﹣72，当x=4时，y=m，‎ ‎∵抛物线向上平移后与线段EF总有公共点，‎ ‎∴m﹣72≤0或m≤12，‎ ‎∴0＜m≤72，‎ 抛物线最多向上平移72个单位；‎ ‎（3）存在符合条件的P点，P点坐标为（2，）或（2，2）；‎ 由（2）得点E（﹣8，0），OC=OE=8，∠CEB=45°，在四边形EMPN中，∠MPN=180°﹣∠CEB=135°（∠PME，∠PNO都是直角）‎ ‎①当∠OPM=75°时，∠OPN=135°﹣75°=60°‎ 在Rt△OPN中，ON=OB=2，sin∠PON==，PN=ON=，即P（2，）；‎ ‎②当∠OPQ=75°时，∠OPN=135°+75°﹣180°=30°，‎ 在Rt△OPN中ON=OB=2，PN=2，‎ 综上所述，存在符合条件的点P，（2，）或（2，2）．‎