初中数学随堂练习(难度系数：040-026)-20180226

初中数学随堂练习(难度系数：040-026)-20180226

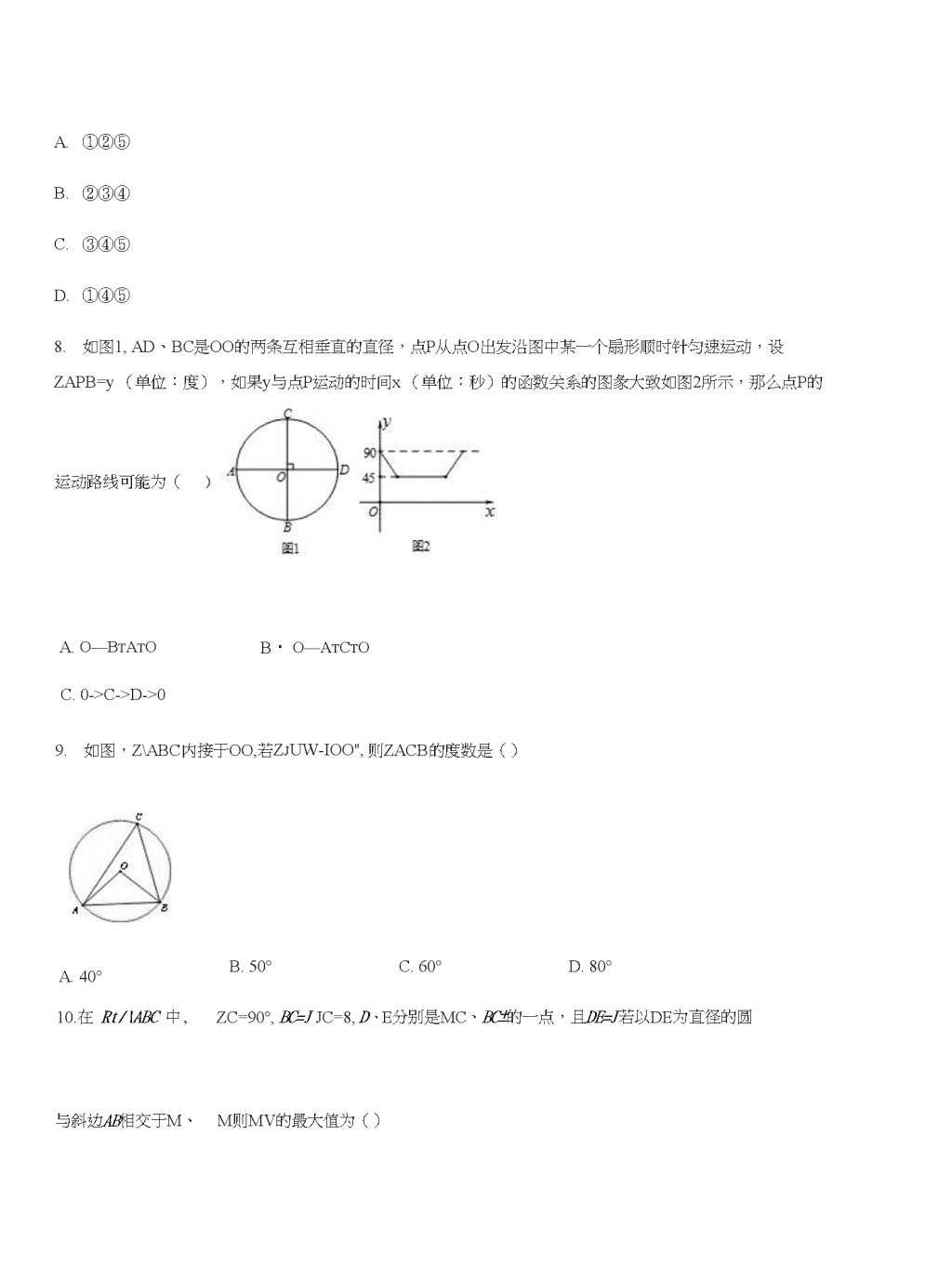
初中数学随堂练习（难度系数：0.40-0.26）-20180226满分：班级：姓名：考号：一、单选题（共20小题）1.B.5OQncn?D.1000"小明作了一顶圆锥形纸帽，已知纸帽底面圆的半径为10cm,母线长为50cm,则圆锥形纸帽的侧面积为为（）A25O«m,C.750兀cm2.如图，Z\ABC内接于OO,AB是OO的直径,ZB=30°,CE平分ZACB交G）O于E,交AB于点D,连接AE,则SaADE：SaCDB的值等于（D.2：3A.1：V2B.1：V3C.1：23•如图，直线AB与OO相切于点A,弓玄CD〃AB,E,F为圆上的两点，且ZCDE=ZADF.若OO的半径为D.6\nA.4的长为4妊，贝I」a的值是（5•如图，在矩形ABCD中，AB=4,AD=5,AD,AB,BC分别与（DO相切于E,F,G三点，过点D作。0的切线BC于点M,切点为N,则DM的长为（)C.6•如图，将沿弦AB折叠，圆弧恰好经过圆心0,点P是优弧乂赢上一点，则ZAPB的度数为（）A.45°B.30°C・75°D.60°7•如图，AB为半圆O的直径，AD、BC分别切OO于A、B两点，CD切（DO于点E,AD与CD相交于D,BC与CD相交于C，连接OD、OC,对于下列结论：®OD=DEC->D->09.如图，Z\ABC内接于OO,若ZjUW-IOO",则ZACB的度数是（）A.40°B.50°C.60°D.80°10.在Rt/\ABC中,ZC=90°,BC=JJC=8,D、E分别是MC、BC±的一点，且DE=J若以DE为直径的圆与斜边AB相交于M、M则MV的最大值为（）\nA.A.C.D・11.已知（DO的半径是4,0P=3,则点P与OO的位置关系是（）B.点P在圆内D.不能确定A.点P在圆上B.点P在圆外12.如图，「ABCD的顶点A.B、D在OO±,顶点C在OO的直径BE上，ZADC=54°,连接AE,则ZAEBA.36°B.46°C.27°D.63°13.如图，OO是aABC的外接圆，ZB=60°,OO的半径为4,则AC的长等于（A.4^3B.6^3C.2^3D.814.CD是OO的一条弦，作直径AB,使AB丄CD,垂足为E,若AB=10,CD=8,则BE的长是（）A.8B.2D.3或715•如图，OO是AABC的外接圆，连结OA、0B,且点C、O在弦AB的同侧，若ZABO50。，则ZACB的度\nC\nA.50°B.45°C.30°D.40°16.如图，A,B,C是OO上的三个点，若ZC=35°,则ZAOB的度数为（A.35°B.55°C・65°D.70°17.如图，OO为AMC的外接圆,ZJ=72°,则ZBCO的度数为（）A.15°B.18°C.20°D.22°18.如图，AABC是OO的内接三角形,ZOAB=35°,则ZACB的度数为（）BB.55°C.60°D.70°19.若扇形的半径为6,圆心角为120%则此扇形的弧长是（A.3兀B.4兀C.5兀D.6兀20•如图，四边形ABCD是菱形，ZA=60°,AB=2,扇形BEF的半径为2,圆心角为60。，则图中阴影部分的面C积是（\nC.—2^—D・兀■二、解答题(共10小题)21.如图，在＜30中，AB,CD是直径，BE是切线，B为切点，连接AD,BC,BD.(1)求证：△ABD9ACDB；(2)若ZDBE=37°,求ZADC的度数.ABE点D在劣弧OA22.如图，在直角坐标系中，(DM经过原点O(0,0)，点A(Jg,0)与点B(0,—逅)，上，连接BD交x轴于点C,MZCOD=ZCBOo(1)求©M的半径；(2)求证：BD平分ZABO；(3)在线段BD的延长线上找一点E,使得直线AE恰为©M的切线，求此时点E的坐标。OC,ZADB=30°.23.如图，在O0中，弦BC垂直于半径OA,垂足为E,D是优弧反上一点，连接BD,AD,(1)求ZAOC的度数；(2)若眩BC=6cm,求图中阴影部分的面积。\n以AB为直径作半圆O,AB=10,点C是该半圆上一动点，连接AC、BC,延长BC至点D,使DOBC,过点D作DE丄AB于点E,交AC于点F,在点C运动过程中：（1）如图1,当点E与点0重合时，连接0C,试判断ACOB的形状，并证明你的结论；（2）如图2,当DE=8时，求线段EF的长；（3）当点E在线段0A上时，是否存在以点E、0、F为顶点的三角形与AABC相似？若存在，请求出此时线段0E的长；若不存在，请说明理由.BB25.如图，形如量角器的半圆0的直径DE=12cm,形如三角板的AABC中，ZACB=90°,ZABC=30°,BC=12cm半圆0以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上.设运动时间为t（s）,当t=Os时，半圆0在AABC的左侧，0C=8cm.（1）当t=8（s）时，试判断点A在半圆0的位置关系；（2）当t为何值时，直线AB与半圆0所在的圆相切；（3）在（2）的条件下，如果半圆面与AABC三边围成的区域有重叠部分，求半圆面与AABC重叠部分的面26.如图，OO是△仙C的外接圆，/C是直径，过点O作OD丄仙于点D,延长DO交OO于点过点卩作PE14C于点、E,作射线DE交BC的延长线于F点，连接PF.（1）若ZPOC=60°,AC=12,求劣弧PC的长；（结果保留兀）（2）求证：OD=OE；（3）求证：PF是OO的切线.4C\n25.已知在平而直角坐标系xOy屮，O是坐标原点，以P(1,1)为圆心的OP与x轴，y轴分别相切于点M和点N,点F从点“出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF,过点PE丄PF交y轴于点E,设点F运动的时间是t秒(t>0)(1)若点E在y轴的负半轴上(如图所示)，求证：PE=PF；(2)在点F运动过程中，设OE=a,OF=b,试用含a的代数式表示b；(3)作点F关于点M的对称点F,经过M、E和F三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中，是否存在某一时刻，使得以点Q、0、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值;若不存在，请说明理由.2&在平面直角坐标系X0冲，直线y=2x+2与兀轴，尹轴分別交于点力，B,抛物线r\y=ax+bx~-经过点/和点C(4,0).(1)求该抛物线的表达式.(2)连接CB,并延长至点D,使请判断点D是否在该抛物线上，并说明理由.(3)在(2)的条件下，过点C作x轴的垂线EC与直线y=2x+2交于点E,以DE为直径画OM,①求圆心M的坐标;1110②若直线肿与相切，P为切点,直接写出点P的坐标.\n29.如图，已知矩形ABCD,AB=12cm,AD=10cm,OO与AD、AB、BC三边都相切，与DC交于点E、F.已知点P、Q、R分别从D、A、B三点同时出发，沿矩形ABCD的边逆时针方向匀速运动，点P、Q、R的运动速度分别是lcm/s、xcm/s、1.5cm/s,当点Q到达点B时停止运动，P、R两点同时停止运动，设运动时间为t（单位：s）（1）求证：DE=CF；(2)设x=3,当QBR相似时，求出t的值;(3)C条件的t，P设APAQ关于直线PQ对称轴的图形是APAQ,当t和x分别为何值时，点A，与圆心O恰好重合，求111符合30.如图①，已知等腰梯形ABCD的周长为48,面积为S,AB〃CD,ZADC=60°,设AB=3x.（1）用x表示AD和CD；（2）用x表示S,并求S的最大值；（3）如图②，当S収最大值时，等腰梯形ABCD的四个顶点都在。O上，点E和点F分别是AB和CD的中点,求（DO的半径R的值.图①三、填空题（共20小题）\n29.如图，直线jr=-yx+3与x轴、y轴分别交于点A、B；点Q是以C(0,-2)为圆心、2为半径的圆上一动4点，过Q点的切线交线段AB于点P,则线段PQ的最小值是30.在平面直角坐标系xOy屮，以原点O为圆心半径为10的圆，直线y=mx・4m+3与G)O交于A、B两点，贝I」弦AB的长的最小值为—.31.如图，AB是的直径，点C是OO上的一点，若BC=6,AB=10,0D丄BC于点D,则0D的长为32.如图，ZAOB=45°，点O在0A上，00尸7,OO|的半径为2,点0?在射线0B上运动，且00?始终与0A相切，当(DO?和相切时，(DO?的半径等于33.如图，AB是的直径，且经过弦CD的中点H,过CD延长线上一点E作(DO的切线，切点为F.若ZACF=65°,则ZE=\n29.如图，将边长为担cm的正方形ABCD沿直线1向右翻动（不滑动），当正方形连续翻动6次后，正方形的屮aCD（B、）（H）心0经过的路线长是cm.（结果保留兀）•…八】0*:…BC（D）I且平行于尸轴的两条平行线围成的阴影38.垂足为D,AD交OO于点E,连接OC、BE,若AE=6,OA=5,则线段DC的\n39.如图，四边形ABCD为（DO的内接四边形，已知ZC=ZD,则AB与CD的位置关系\n40•小明四等分倉，他的作法如下：(1)连接AB(如图)；(2)作AB的垂直平分线CD交窗于点M,交AB于点T；(3)分别作AT,TB的垂直平分线EF,GH,交再于N,P两点.则N,M,P三点把倉四等分.你认为小明的作法是否正确：，理由是.41•如图，RtAABC中，ZBAC=90°,AB=AC=2,以AB为直径的圆交BC于点D,则阴影部分面积为0242.—个扇形的圆心角为120,面积为127icm,则此扇形的半径为cm.43.如图，OO的半径是2,直线2与OO相交于A、B两点，M、N是。O上两个动点，且在直线2的异侧，若ZAMB=45°,则四边形MANB面积的最大值是44.如图，点C在以AB为直径的半圆上，AB=8,ZCBA=30°,点D在线段AB上运动，点E与点D关于AC对称，DF丄DE于点D,并交EC的延长线于点F.下列结论：①CE=CF；②线段EF的最小值为2苗；③当AD=2\n面积是1胡•其中正确结论的序号是42.如图，以BC为直径的。Ch与OO?外切，与的外公切线交于点D,且ZADO60。，过B点的G)Ch的切B线交其中一条外公切线于点A.若002的面积为兀，则四边形ABCD的面积是43.如图，已知AB是厶ABC外接圆的直径，ZA=35°,则ZB的度数是44.如图，Za=120°,Zp=90°.则Zy的度数是\n度.42.如图，点A,B,C是G>0上的点，AO=AB,则ZACB=\n上，如果动点P满足ZAPB=90°,（1）线段OP的长等于—（用含m的代数式表示）；（2）m的最小值为50•如图，小明从纸上剪下一个圆形和一个扇形纸片，用它们恰好能围成一个圆锥模型.若圆的半径为1,扇形的四、计算题（共10小题）51.如图，在正方形网格屮，AABC各顶点都在格点上，点A,C的坐标分别为（・5,1）、（-1,4）,结合所给的平面直角处标系解答下列问题：（1）画出AABC关于y轴对称的厶（2）画出AABC关于原点O对称的△A2B2C2；（3）点G的坐标是点C2的坐标是过C、C|、C2三点的圆的圆弧CC%的长是（保留兀）•A••••mi・・・■■・・••••••\n（1）求证：BC是的切线;51.有A、B两个不透明的布袋，A袋中有两个完全相同的小球，分别标有数字0和・2；B袋中有三个完全相同的小球，分别标有数字・2、0和1.小明从A袋屮随机取出一个小球，记录标有的数字为x,再从B袋屮随机取出一个小球，记录标有的数字为y,这样确定了点Q的坐标（x,y）.（1）写出点Q所有可能的坐标；（2）求点Q在x轴上的概率；（3）在平面直角坐标系xOy中，OO的半径是2,求过点Q能作切线的概率.52.如图，在OO屮，半径OC与弦AB垂直，垂足为E,以OC为直径的圆与眩AB的一个交点为F,D是CF延长线与O0的交点.若0E=4,0F=6,求（DO的半径和CD的长.53.如图，AB是的直径，点E是奩上的一点，ZDBOZBED.54.如图，PA,PB是OO的切线，A,B为切点，AC是＜30的直径，ZP=50°,求ZBAC的度数。\n51.如图，点0为RtAABC斜边AB±的一点，以0A为半径的（D0与BC切于点D,与AC交于点E,连接\nAD.EDAOB（1）求证：AD平分ZBAC；（2）若ZBAC=60°,OA=2,求阴影部分的面积（结果保留＞）.51.如图所示，AB是0O的直径，AD与0O相切于点A,DE与OO相切于点E,点C为DE延长线上一点，且CE=CB.（1）求证：BC为0O的切线；（2）若AB=4,AD=1,求线段CE的长.5&如图，OO的直径为点C在圆周上（异于人,4D丄CD.（1）若BC=3,#8=5,求4C的值；（2）若M是的平分线，求证：直线C©是OO的切线.59.如图1,-辆汽车的背面，有一种特殊性状的刮雨器，忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示，量得连杆OA长为10cm,雨刮杆AB长为48cm,ZOAB=120°.若启动一次刮雨器，雨刮杆AB正好扫到水平线CD的位置，如图3所示.（1）求雨刮杆AB旋转的最大角度及O、B两点之间的距离；（结果精确到0.01）\n尿1=26.851,可使用科学记算器）59.如图1,-辆汽车的背面，有一种特殊形状的刮雨器，忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示，量得连杆OA长为10cm,雨刮杆AB长为48cm,ZOAB=120°.若启动一次刮雨器，雨刮杆AB正好扫到水平线CD的位置，如图3所示.（1）求雨刮杆AB旋转的最大角度及O、B两点之间的距离；（结果精确到0.01）（2）求雨刮杆AB扫过的最大面积.（结果保留兀的整数倍）（参考数据：sin60°=2^.,cos60°=,tan60°=^3»-/721-26.851,可使用科学计算器）五、证明题（共5小题）60.如图，AB是OO的直径，点C是＜30上一点，ZBAC的平分线AD交OO于点D,过点D垂直于AC的直线交AC的延长线于点E.（1）求证：DE是OO的切线;（2）如图AD=5,AE=4,求。0的直径.\n59.已知：如图，AABC内接于00,AB为直径，ZCBA的平分线交AC于点F,交OO于点D,DE丄AB于点E,且交AC于点P,连结AD.（1）求证：ZDAOZDBA；\nDCBE0(2)求证：P是线段AF的中点;(1)连接CD,若CD=3,BD=4,求G)O的半径和DE的长.59.如图，已知点C是以AB为直径的OO±一点，CH丄AB于点H,过点B作OO的切线交直线AC于点D,点E为CH的屮点，连接AE并延长交BD于点F,直线CF交AB的延长线于G.(1)求证：AE・FD=AF・EC；(2)求证：FC=FB；(3)若FB=FE=2,求OO的半径r的长.60.如图，AB,BC,CD分别与(DO相切于E,F,G.且AB〃CD.B0=6cm,C0=8cm.(1)求证：BO丄CO；(2)求BE和CG的长.61.如图，AABC屮，ZACB=90°,D是边AB上一点，且ZA=2ZDCB.E是BC边上的一点，以EC为直径的OO经过点D.\n(1)求证：AB是OO的切线;(2)若CD的弦心距为1,BE=EO,求BD的长.AC六、作图题(共5小题)59.如图，方格纸屮每个小正方形的边长都是单位1,AABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：(1)将AABC向右平移3个单位长度再向下平移2个单位长度，画出两次平移后的△A|B|G；(2)写!1!AnG的坐标；(3)将△A|B|G绕G逆时针旋转90。，画出旋转后的△A2B2G，求线段BG旋转过程屮扫过的而积(结果保留60.如图，在平面直角坐标系中，AABC的三个顶点坐标为A(1,-4),B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形)(1)将AABC沿y轴方向向上平移5个单位，画出平移后得到的△AQ】。；\n6&如图AB是半圆的直径，图1屮，点C在半圆外；图2屮，点C在半圆内，请仅用无刻度的直尺按要求画图.（1）在图1屮，画出AABC的三条高的交点；（2）在图2中，画1UAABC中AB边上的高.69.如图，跷跷板AB的一端B碰到地面时，AB与地面的夹角为15。，且OA=OB=3m.（1）求此时另一端A离地面的距离（精确到0.1m）；（2）若跷动AB,使端点A碰到地面，请画出点A运动的路线（不写画法，保留画图痕迹），并求出点A运动路线的长.（参考数据:sinl5°^0.26,cosl5°^0.97,tanl5°^0.27)70.(1)如图，点E、F在AC±,AB〃CD,AB=CD,AE=CF.求证：△ABF9Z\CDE.（2）如图，方格纸屮的每个小方格是边长为1个单位长度的正方形.①画出将RtAABC向右平移5个单位长度后的RtAA^^u②再将RtAA1B1G绕点G顺时针旋转90°,画出旋转后的RtAABC!,并求出旋转过程中线段入0所扫过的面积（结果保留7T）.答案部分\n试题解析：底面圆的半径为叭，则底面周长沁g侧面面积专X205500Z选B答案：B2.考点：圆的综合题试题解析：TAB是（DO的直径,.\ZACB=90o,VZB=30°,VCE平分ZACB交(DO于E,・ACADV3，BD=V^3AB，过C作CE丄AB于E,连接OE,VCE平分ZACB交(DO于E,••AE=DE，AOE丄AB,AOE=^AB,CE=^AB,24ASaADE：SaCDB=(^ADOE):(&BDCE)=丄AB):X-i=^—AB-^AB)=2：3.22273+322乂3+34C答案：D3.考点：切线的性质与判定圆周角定理及推论垂径定理及推论试题解析：此题考查了切线的性质、圆周角定理、垂径定理以及勾股定理等知识.此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用.首先连接OA,并反向延长交CD于点H,连接OC,由直线AB与00相切于点A,眩CD〃AB,可求得OH的长，然后由勾股定理求得AC的长，又由ZCDE=ZADF,可证得EF=AC,继而求得答案.解:连接0A,并反向延长交CD于点H,连接0C,\n・・•直线AB与00相切于点A,AOA丄AB,•・•弓玄CD〃AB,・・・AH丄CD,.\CH=4cD=4x4=2,22・・・。0的半径为号,・・・OA=OC=专，.-.oh^/oc2-ch2=|.•-AH=OA+OH=aac=7aH2+CH2=2V5-VZCDE=ZADF,••B*-Bb，・•・EF=AC=2a/5.答案：B2.考点：圆的综合题试题解析：作PC丄x轴于C,交AB于D,作PE丄AB于E,连结PB,如图,VQP的圆心坐标是（3,a）,:.0C=3,PC=a,把x=3代入y=x得y=3,・・・D点坐标为（3,3）,・・・CD=3,•••△OCD为等腰直角三角形，・•・APED也为等腰直角三角形，VPE丄AB,AAE=BE=^AB=2V2在RtAPBE中，PB=3\n・・・PE=1答案：B2.考点：矩形的性质和判定切线的性质与判定直角三角形与勾股定理试题解析：试题分析：连接OE,OF,ON,0G,在矩形ABCD中，VZA=ZB=90°,CD=AB=4,TAD,AB,BC分别与OO相切于E,F,G三点，AZAEO=ZAFO=ZOFB=ZBGO=90°,二四边形AFOE,FBGO是正方形，.\AF=BF=AE=BG=2,・\DE=3,VDM是G)O的切线，DN=DE=3,MN=MG,ACM=5-2-MN=3-MN,在*=也，・•・(3+卿尸=(3—昶疔“，ADM=3+-=—,故选33RtADMC中,答案：A3.考点：圆周角定理及推论图形的翻折试题解析：解：作半径0C丄AB于D,连结OA、0B,如图,•・•将OO沿弦AB折叠，圆弧恰好经过圆心0,AOD=CD,.•.od=Loc=Loa,22:.ZOAD=30°,rfn0A=OB,\n•••ZCBA=30°,AZAOB=120°,AZAPB=-ZAOB=60°.2答案：D2.考点：切线的性质与判定相似三角形判定及性质全等三角形的判定全等三角形的性质试题解析：连接0E,如图所不：VAD与圆0相切，DC与圆0相切，BC与圆0相切,・・・ZDA0=ZDEO=ZOBC=90°,・・・DA=DE,CE=CB,AD〃BC,ACD=DE+EC=AD+BC,选项②正确;在RtAADO和RtAEDO中,(OD二OD(DA=DEARtAADO^RtAEDO(HL),.•.ZAOD=ZEOD,同理RtACEO^RtACBO,AZEOC=ZBOC,又ZAOD+ZDOE+ZEOC+ZCOB=180°,・・・2(ZDOE+ZEOC)=180°,即ZDOC=90°,选项⑤正确;・・・ZDOC=ZDEO=90°,又ZEDO=ZODC,AAEDO^AODC,・・・晋=警，即OD=DC*DE,选项①正确；[来源:学。科。网Z。X。X。K]而S梯形ABCD=^AB・(AD+BC)=^AB*CD,选项④错误；由OD不一定等于OC,选项③错误,则正确的选项有①②⑤.\n故选A答案：A8•考点：圆的综合题试题解析：根据题意可得y先减小后45。不变再增大，所以路线应为O->CtDtO.故选C答案：C9.考点：圆周角定理及推论试题解析：厶00.100"，厶丄厶00=丄故选B22答案：B10.考点：直线与圆的位置关系相似三角形判定及性质试题解析：当圆心到MN距离d最短时，MN值最大，即MN〃DE以C点为原点，以CB所在直线为X轴，以CA所在直线为Y轴建系XOY设DE的中点为0点・・•ZC=90°BC=6,AC=8所以AB=10AAECD^ABCA9解得CE=-CD=32所以o(—,—)直线AB的解析式为3y+4x-24=093、•:点0(■,■)到直线3y+4x・24=0的距禺42924d=・故MN=—55答案：A11.考点：点与圆的位置关系试题解析：・・・OP=3<4,故点P与OO的位置关系是点在圆内故选B答案：B12•考点：与圆有关的概念及性质\n试题解析：解：•・•四边形ABCD是平行四边形，ZADC=54°,AZB=ZADC=54O,•・・BE为（DO的直径，.•.ZBAE=90°,ZAEB=90°・ZB=90°・54°=36°.故选A答案：A13•考点：直角三角形与勾股定理与圆有关的概念及性质试题解析：连接OA,OC,过点0作OD丄AC于点D,VZA0C=2ZB,且ZAOD=ZCOD=^ZAOC,AZCOD=ZB=60°；在RtACOD中，004,ZCOD=60°,・・・CD=¥oC=2屈・・・AC=2CD=4屈答案：A14.考点：垂径定理及推论试题解析：图2连结0C,由垂径定理可知：CE=4由勾股定理可得：08==3\n所以，Eff=5-3=2同理，如图2,Aff=54-3=8答案：B15•考点：圆周角定理及推论试题解析：・・・OA=OB,AZBAO=ZABO=50°,・・・ZAOB=180°・50°・50°=80°.ZACB=4zAOB=40°.2故选D.答案：D16•考点：圆周角定理及推论试题解析:•・•ZAOB=2ZACB,ZAOB=70°,・•・ZAOC=-ZAOB=-x70°=35°.故选D.答案：D17.考点：圆周角定理及推论试题解析：连接BO,VZA=72°f:.ZBOC=144°,AZBCO=(180°-144°)-2=18°.故选B.答案：B18.考点：圆周角定理及推论试题解析：TOA=OB,.•.ZOAB=ZOBA=35°,AZAOB=180°-35°x2=l10°,AZACB=-ZAOB=55°;2答案：B19.考点：扇形面积的计算试题解析：根据弧长的公式匸唏进行计算即可.1oU解：・・•扇形的半径为6,圆心角为120。,・・・此扇形的弧长.答案：B\n17.考点：菱形的性质与判定扇形面积的计算试题解析：连接BD,•・•四边形ABCD是菱形，ZA=60°,AZADC=120°,AZl=Z2=60°,AADAB是等边三角形，VAB=2,AAABD的高为石，・.•扇形BEF的半径为2,圆心角为60。，AZ4+Z5=60°,Z3+Z5=60°,AZ3=Z4,设AD、BE相交于点G,设BF、DC相交于点H,在AARG和ZiDBH中，Z^=Z2•把•••△ABG9ADBH(ASA),・••四边形GBHD的面积等于△ABD的面积，.••图中阴影部分的面积Z3=Z4答案：B18.考点：圆周角定理及推论切线的性质与判定全等三角形的判定试题解析：此题考查了切线的性质、圆周角定理及其推论以及全等三角形的判定和性质•(1)根据AB,CD是直径，可得出ZADB=ZCBD=90。，再根据HL定理得illAABD^ACDB；(2)由BE是切线，得AB丄BE,根据ZDBE=37°,得ZBAD,由OA=OD,得出ZADC的度数.(1)证明：TAB,CD是直径.\ZADB=ZCBD=90o在AABD和Z\CDB中,AAABD和厶CDB(HL)(2)解:VBE是切线AAB丄BE.\ZABE=90oJZDBE=37°・•・ZABD=53°VOA=OD・・・ZBAD=ZODA=90°-53°=37°AZADC的度数为37。.答案：(1)证明见解析过程；(2)37。19.考点：角及角平分线切线的性质与判定\n试题解析：/.OA=j6OB=^・・・根据RtAAOB的勾股定理可得:・・・0M的半径r=（1）・・・点A为（歯，0），点B为（0,—忑）AB=2返（2）根据同弧所对的圆周角相等可得：ZABD=ZCODVZCOD=ZCBO・\ZABD=ZCBO・・・BD平分ZABO（3）如图，由（2）屮的角平分线可得AABE竺AHBEABH=BA=2^2：・OH=2忑_忑=返在RtAAOBAZCBO=30°在RtAHBE中,HE=•••点E的坐标为（竽,答案：(1)渥；(2)见解析；(3)(孝，运)17.考点：垂径定理及推论直角三角形与勾股定理圆周角定理及推论扇形面积的计算试题解析：解:(1)VBC1OA,ABE=CE,AB=AC，又VZADB=30°,・•・ZAOC=ZAOB=2ZADB,・・・ZAOC=60°；(2)VBC=6,・・・CE=^BC=3,CFl在RtAOCE中，OC=.=2屈smoO・•・OE=^0C2一CE2=x/4X3-9=V^，连接OB,7AB=AC，AZBOC=2ZAOC=120°,••S阴形=S用形oBC-SaoBC\n120=-TT7x兀x360=471-3a/3-答案：见解析17.考点：圆的综合题试题解析：解：（1）ACOB是等边三角形;理由如下：VDE丄AB,AZDOB=90°,又・・・DC=BC・・・OC=BC,•••OOBOOB,•••△COB是等边三角形；（2）解：连接AD,VAB为圆O的直径，・•・ZACB=90°,又・・・DC=BC,.\AD=AB=10,・•・AE=7aD2-DE2=V102-82=6，・•・EB=4；又VZB+ZBAC=90°,ZB+ZBDE=90°,AZBAC=ZBDE,.•.AAEF^ADEB,.EF_AE•■~—9EBDE•••EF=3；(1)答；存在，当Z\OEF和AABC相似时，①如图3,若ZFOE=ZCAB,则OF=AF,XVDE丄AB,0E二AE二0A5\n②如图4,若ZEOF=ZCBA,贝ijOF〃BD,•OF_1•■—«BC2.OF_1•■—9BD4・OE_OF_1••——,BEBD4.QE_1…丽応肓综上所述：OE的长为£或D答案：见解析解：(1)当t=8时,25•考点：点与圆的位置关系直线与圆的位置关系阴影部分图形的相关计算试题解析：此时OC=8,在RtAACO中，AC=4眉，则AO=4衙＞6,所以点A在半圆外；(2)①如图1,过C点作CF丄AB,图1VZABC=30°,BC=12cm,・°・FO=6cm；当半圆O与AABC的边AB相切时,\n又・・•圆心O到AB的距离等于6cm,且圆心0乂在直线BC上，・・・0与C重合，即当0点运动到C点时，半圆0与AABC的边AB相切；此时点0运动了8cm,所求运动时间为1=号=4(s),②当点O运动到B点的右侧，且OB=12cm时，如图2,过点0作0Q丄直线AB,垂足为在RtAQOB中,ZOBQ=30°,则0Q=6cm,即0Q与半圆0所在的圆相切.此时点0运动了32cm.所求运动时间为：t=32^-2=16s,综上可知当t=4s或16s时，AB与半圆O所在的圆相切;(3)当半圆O与AB边相切于M时，如图1,答案：见解析26.考点：弧长计算全等三角形的判定全等三角形的性质相似三角形判定及性质切线的性质与判定试题解析：(1)VJC=12,・•・CO6,a180(2)•:PE丄力C,OD丄4B,(ZAD0二ZPEO在厶ADO和/XPEO中，ZA0D=ZP0E10ARC:./\POE^/\AOD(AAS),：・OD=EO；(1)如图，连接力尸，PC,•；OA=OP,:.ZOAP=ZOPA,由（1）得OD=EO,:.ZODE=ZOED,又•・・ZAOP=ZEOD,\n・•・Z0P4=Z0DE,:.APIIDF.'：AC是直径，・・・ZAPC=90°f:.ZPQE=90°:.PC丄EF,丈：DP〃BF,・・・上ODE=ZEFC,・.・ZOED=ZCEF,:.kCEF=ZEFC,:.CE=CF,：・PC为EF的中垂线,・・・ZEPQ=ZQFF,•:HCEPsHCAP:.kEPQ=ZEAP,:.ZQPF=ZEAP,:.乙QPF=/OPA,IZOR4+ZOPC=90。,・•・ZOPF+ZOPC=90。,：.0P丄PF,・・・PF是（DO的切线.答案：（1）2兀（2）见解析（3）见解析27.考点：切线的性质与判定相似三角形判定及性质全等三角形的判定试题解析：本题主要考查了圆的综合题，解题的关键是把圆的知识与全等三角形与相似三角形相结合找出线段关系.（1）连接PM,PN,运用△PMF^APNE证明，（2）分两种情况①当t>1时，点E在y轴的负半轴上，OVt口时，点E在y轴的正半轴或原点上，再根据（1）求解，（3）分两种情况，当l2时，三角形相似时还各有两种情况，根据比例式求出时间t・证明：（1）如图，连接PM,PN,VOP与x轴，y轴分别相切于点M和点N,\n・・・PM丄MF,PN丄ON且PM=PN,・•・ZPMF=ZPNE=90°且ZNPM=90。，•「PE丄PF,ZNPE=ZMPF=90°-ZMPE,（ZNPE=ZMPF在APNIF和APNE中，\PN=PM[zpne=zpmf（2）解：分两种情况：①当t>l时，点E在y轴的负半轴上，如图1,由（1）得厶PMF^APNE,ANE=MF=t,PM=PN=1,・・.b=OF=OM+MF=l+t,a=NE・ON=t・1,Ab-a=l+t-（t-1）=2,•:b=2+a,②OVtS时，如图2,点E在y轴的正半轴或原点上,'yNE/MFW'图2同理可证APN/IF竺ZXPNE,・・.b=OF=OM+MF=l+t,a=ON・NE=1・t,/.b+a=l+t+l-t=2,・°・b=2-a,综上所述，当t>l时，b=2+a；当0VtWl时，b=2-a；（3）存在；\nVF(1+t,0),F和F关于点M对称，M的坐标为(1,0),・・・F(1・t,0)•・•经过M、E和F三点的抛物线的对称轴交x轴于点Q,Q(1-4,0)・・・OQ=1■寺,由(1)得厶PMF^APNEANE=MF=t,OE=t-1当厶OEQs/iMPF...OE=OQMP~MF解得,L1+茫,4当Z\OEQ^AMFP时,.OE=OQt-lW而t1解得,t=V2,\n②如图4,当t>2时,VF(1+t,0),F和F关于点M对称，・・・F(1・t,0)•・•经过M、E和F三点的抛物线的对称轴交x轴于点Q,・・・Q(1-寺，0)・•・OQ兮-1,由(1)得厶PMF^APNEANE=MF=t,・・・OE=t-1当△()EQ^AMPF.0E=0Q无解，当厶OEQs/\MFP时,.0E=0Qt-1**MF~MP，t1解得，t=2土Ji所以当t—]+茫,t=2土血时，使得以点Q、0、E为顶点的三角形与以点P、M、F为顶点的三角形相似.\n答案：(1)见解析过程(2)当t>l时，b=2+a；当OVtSl时,b=2-a；(3)存在,t=V2，t=2±V228.考点：二次函数表达式的确定相似三角形判定及性质与圆有关的概念及性质试题解析：(1)依题意，可知/(-1,0),B(0,2).抛物线y=ax+bx~^经过点力，C(4,0)所以有2O—A——=0>3■2i&i+4*--=a3(2)点D在该抛物线上.依题意，可得BO=2,CO=4.过点D作DF垂直x轴于点F,:./\CDFs£CBO・:.DF=4,OF=CF・OC=4.討(诃号(7)弓・4,・••点D在该抛物线上.(3)①由题意可知E(4,10).设DE与y轴的交点为.WDBSBAtf1CB・・M即撷的圆心―皿■护d:.M(0,7)・\ny②(-4,4)或(3,3)・112答案：（1）一一X一一（2）点Q在该抛物线上.（3）①M（0,7）②（-4,4）或（3,3）62329.考点：圆的综合题试题解析：（1）证明：作OG丄EF于G,设OO与AD边相切于M,连接MO并延长交BC于N,如图1所示:则MN丄AD,・・•四边形ABCD是矩形，・・・AD〃BC,AMN丄BC,VBC是OO的切线，・・・N为切点，・・・四边形CDMN是矩形，・・・MN=CD,VOG丄CD,・・・DG=CG,EG=FG,・•・DE=CF；（2）解：分两种情况：®x=3时，00创，ZA=ZB,当厶PAQ-AQBR时，詈疇,②当Z\PAQsZ\rbQ时，霍令,BRBQ即罟価解得：t=2A/g9~14；综上所述：t的值为¥或2何-14；b（3）解：如图2所示：根据题意得：AA，被直线PQ垂直平分,•••△APQ为等腰直角三角形，AP=AQ=6,\n答案：见解析29.考点：垂径定理及推论直角三角形与勾股定理试题解析：解：(1)作AH丄CD于H,BG丄CD于G,如图①,则四边形AHGB为矩形，HG=AB=3x,•・・四边形ABCD为等腰梯形，AAD=BC,DH=CG,在RtAADH^I',设DH=t,•・•ZADC=60°,.•.ZDAH=30°,・・・AD=2t,AH=J瓦，BC=2t,CG=t,・・•等腰梯形ABCD的周长为48,3x+2t+t+3x+t+2t=48,解得t=8-x,/.AD=2(8-x)=18-2x,CD=8・x+3x+8・x=l6+x；(2)S=*(AB+CD)・AH\n=~(3x+16+x)•忑(8-x)乙=-2a/3x+8価\+64馅，•/S=-2a/3(x-2)+72a/3，・••当x=2时，S有最大值72^3；(3)连结OA、OD,如图②，当x=2时,AB=6,CD=16+2=18,等腰梯形的高为^/^x(8-2)=6^3»贝ljAE=3,DF=9,・・・点E和点F分别是AB和CD的中点，・•・直线EF为等腰梯形ABCD的对称轴，・・・EF垂直平分AB和CD,EF为等腰梯形ABCD的高，即EF=6馅,・••等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6品a,在RtAAOE中，222JOE+AE=OA,222/•a+3=R,在RtAODF屮，vof2+df2=od2,(6V3-a)+9=R,a+3=(6』^・a)+9,解得a=5j^,R=(5a/3)2+3=84,・・・R=2近L图①答案：见解析29.考点：切线的性质与判定试题解析：过点C作CP丄直线AB与点P,过点P作（DC的切线PQ,切点为Q,此时PQ最小连接CQ,由点到直线的距离求出CP的长度，再根据勾股定理即可求出PQ的长度.过点C作CP丄直线AB与点P,过点P作OC的切线PQ,切点为Q,此时PQ最小，连接CQ,如图所示.3直线AB的解析式为y=-亍x+3，即3x+4y-12=0,•••点C(0,・2)cp=^^=4・・・PQ为（DC的切线,\n・・・在RtZkCQP中,CQ=2,•:PQ=VcP^-Cq2=2^答案：2^332•考点：圆的综合题・・•点D的坐标是（4,3）,・・・0D=5,・・・。0的半径为10,AA（10,0）,AOB=10,：•BD=J。沪一皿丄=/沪-必=扬,ABC的长的最小值为1朋.答案：1话33.考点：圆的综合题相似三角形判定及性质试题解析：根据AB为直径可得ZC=90°,根据RtAABC的勾股定理可得AC=8,根据OD丄BC可得△BODs^BAC,答案：4\n34.考点：圆与圆的位置关系试题解析：本题考查了圆与圆的位置关系，解题的关键是正确的作出图形，作O2C丄0A于点C,连接0Q2,设O2C=r,根据解:如图，作O2C丄0A于点C,连接0Q2,OOi的半径为2,00|=7,表示Ji!O|O2=r+2,设ChC=r,VZAOB=45°,AOC=O2C=r,・・・。0|的半径为2,00,=7,.*.O]O2=r+2,0]C=7-r,222(7-r)+r=(r+2),解得：r=3或15,故答案为：3或15.答案：3或1535•考点：切线的性质与判定与圆有关的概念及性质试题解析：解：连接DF,连接AF交CE于G,VAB是OO的直径，II经过弦CD的中点H,・••盘二亦，VEF是。0的切线,・•・ZGFE=ZGFD+ZDFE=ZACF=65°,・・•ZFGD=ZFCD+ZCFA,VZDFE=ZDCF,ZGFD=ZAFC,ZEFG=ZEGF=65°,\nZE=180°・ZEFG・ZEGF=50°,故答案为:答案：50°36.考点：弧长计算正方形的性质与判定图形的旋转试题解析：D⑻XOB(D)C(J)(D)e打、*BC(D)(J)(P)(Q・・•正方形ABCD的边长为砲cm,・・・正方形的对角线长是lcm,翻动一次屮心经过的路线是半径是对角线的一半为半径，圆心角是90度的弧.则中心经过的路线长是：°。蔦j1x6=307icm；loU故答案是：30兀.答案：30ti37.考点：阴影部分图形的相关计算试题解析：根据题意得:根据填补法，将x轴以上的阴影面积填补到x轴下面，以y=・2为分界，将y二2以下的阴影面积填补到y=0到尸・2这个区域内，这样就构成了一个长方形。所以面积为8。答案：838•考点：直线与圆的位置关系试题解析：TAB为OO的直径，・•・£!胭=时，在TCTAASB屮，AE=6,AB=2OA=10,则BE=历頁VAD丄1,=,・•・DC//BE,・・•直线1与OO相切于点C,：・厶OCD=yf,\n贝IJOC1EB.EF=—SB=4.2可推得四边形为DEGC为矩形,贝ijDC=EG=4.答案：439.考点：圆周角定理及推论试题解析：•・•四边形ABCD为的内接四边形，・・・ZA+ZC>180。又•・•/(>,D,.•.ZA+ZD=180°.・・・AB〃CD.答案：AB〃CD.40.考点：垂径定理及推论试题解析：不正确，在第(3)中，打、帀不是弦，所以此种作法不正确。答案：不正确，M、7W不是弦；41.考点：扇形面积的计算试题解析：女(1图，VRtAABC中，ZBAC=90°,AB=AC=2,典近:・BC=AC=2,SAABC=-^ACxAB=^x2x2=2.又VAB是圆O的直径，AZADB=90°,即AD丄BC,AAD是斜边BC±的中线，・\SAABD=4sAABC=1.AS阴影=S半圆-SAABD=4rxl2-1=--1.222答案：啓-1242.考点：扇形面积的计算试题解析：12兀='"代,求得r=6cm.360答案：643.考点：圆周角定理及推论试题解析：过点O作OC丄AB于C,交G>O于D、E两点，连结OA、OB、DA、DB、EA、EB,根据圆周角定理得ZAOB=2ZAMB=90°,则AOAB为等腰直角三角形，所以AB=^OA=2运，由于S㈣边形MANB=S/.MAB+SaNAB,而当M点到AB的距离最大，/XMAB的面积最大；当N点到AB的距离最大时，\nANAB的面积最大，即M点运动到D点，N点运动到E点，所以四边形MANB面枳的最大值：S四边形DAEB=SaDAB+S^EAB=—AB・CD+—AB・CE=—AB(CD+CE)222\nMD=2AB-DE=-x2^x4=4^.22N解：过点o作OC丄AB于C,交OO于D、E两点，连结OA、OB、DA、DB、EA、EB,如图，VZAMB=45°,.•.ZAOB=2ZAMB=90°,•••△OAB为等腰直角三角形，AB=血OA=2,：・S四边形MANB=S^MAB+SaNAB,S四边形・••当M点到AB的距离最大，AMAB的面积最大；当N点到AB的距离最大时，ANAB的面积最大，即M点运动到D点，N点运动到E点，此时四边形MANB面积的最大值：DAEB=SaDAB+SaEAB=―AB*CD+—AB*CE=—AB(CD+CE)=—AB*DE=—x2^5x4=4.22222答案：4近42.考点：平行线的判定及性质相似三角形判定及性质切线的性质与判定轴对称与轴对称图形试题解析：本题考查了等边三角形的判定与性质、平行线的判定与性质、相似三角形的判定与性质、切线的判定、轴对称的性质、含30。角的直角三角形、垂线段最短等知识.（1）由点E与点D关于AC对称可得CE=CD,再根据DF丄DE即可证到CE=CF.（2）根据“点到直线之间，垂线段最短"可得CD丄AB时CD最小，由于EF=2CD,求出CD的最小值就可求出EF的最小值.（3）连接OC,易证AAOC是等边三角形，AD=OD,根据等腰三角形的“三线合一”可求出ZACD,进而可求出ZECO=90°,从而得到EF与半圆相切.（4）利用相似三角形的判定与性质可证到AOBF是等边三角形，只需求出BF就可求；1|DB,进而求出AD长.（5）首先根据对称性确定线段EF扫过的图形，然后探究出该图形与AABC的关系，就可求出线段EF扫过的面积.图1解：：①连接CD,如图1所示.・・•点E与点D关于AC对称，・・・CE=CD..\ZE=ZCDE.\n•・・DF丄DE,・•・ZEDF=90°.・・・ZE+ZF=90°,ZCDE+ZCDF=90°..\ZF=ZCDF.・・・CD=CF.・・・CE=CD=CF.・•・结论“CE=CF''正确.图2②当CD丄AB时，如图2所示.VAB是半圆的直径，.•.ZACB=90°.VAB=8,ZCBA=30°,AZCAB=60°,AC=4,BC=4苗・VCD丄AB,ZCBA=30°,・・・CD=|BC=2•根据“点到直线之间，垂线段最短"可得：点D在线段AB上运动吋，CD的最小值为2VCE=CD=CF,・・・EF=2CD.・・・线段EF的最小值为4J5・・・・结论“线段EF的最小值为2错误.图3③当AD=2时，连接OC,如图3所示.VOA=OC,ZCAB=60°,•••△OAC是等边三角形.・・・CA二CO,ZACO=60。.VAO=4,AD=2,\nD0=2・・・・AD=DO..\ZACD=ZOCD=30°.•・•点E与点D关于AC对称,.\ZECA=ZDCA.・・・ZECA=30°.・・・ZECO=90。.・・・0C丄EF.•・・EF经过半径OC的外端，且OC丄EF,・・・EF与半圆相切.・・・结论“EF与半圆相切”正确.②当点F恰好落在fib上时，连接FB、AF,如图4所示.・・•点E与点D关于AC对称,・・・ED丄AC..•.ZAGD=90°.AZAGD=ZACB.・・・ED〃BC.AAFHC^AFDE.・FHK••■nhVFC=-EF,2FH=1FD・2.•.FH=DH.•・・DE〃BC,AZFHC=ZFDE=90°.ABF=BD..\ZFBH=ZDBH=30o.・・・ZFBD=60。.VAB是半圆的直径，・•・ZAFB=90°.・•・ZFAB=30°・AFB=1aB=4.2\n・・・DB=4.\nAAD=AB-DB=4.・•・结论“AD=2运"错误.②•・•点D与点E关于AC对称,点D与点F关于BC对称,・・・当点D从点A运动到点B时,ADOB图5点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称.・・・EF扫过的图形就是图5中阴影部分.••S阴形=2S^ABC=2x1aC*BC2=AC・BC=4x4J5=16苗・・・・EF扫过的面积为16J5.・・・结论“EF扫过的面积为16帀"正确.故答案为：①、③、⑤.答案：①③⑤42.考点：圆与圆的位置关系直角三角形与勾股定理矩形的性质和判定切线的性质与判定试题解析：解：・・・。02的面积为兀，aoo2的半径是1,VAB和AH是（DO】的切线，・・・AB=AH,设（DO?的半径是R,连接D02,DOi，02E,0|H,AOp作O2F丄BC于F,V0O1与OO2外切,OOi与（DO?的外公切线DC.DA,ZADC=60°,AD.O2、Ch三点共线，ZCDO】=30。，・•・ZDAOl60。，ZO2EC=ZECF=ZCFO2=90o,・・・四边形cfo2e是矩形，.\O2E=CF,CE=FO2,ZFO2O严ZCDO严30。，\nADO2=2O2E=2,ZHAO,=60°,R+l=2(R-l),解得：R=3,即DO,=2+l+3=6,在RtACDO!中，由勾股定理得：CD=3笛，VZHO!A=90o-60o=30°,HO,=3,AH=^/3=AB,・•・四边形ABCD的面积是：*(AB+CD)xBC=*(馅+3灵)x(3+3)=12^.故答案为:答案：42.考点：与圆有关的概念及性质试题解析：TAB是直径.\ZACB=90°JZA=35°AZB=65°答案：65°43.考点：与圆有关的概念及性质试题解析：三个角构成了一个周角°+卩卄=360。答m：15044.考点：圆周角定理及推论试题解析：因为点A,B,C是OO上的点，AO=AB,所以OA=OB=AB,所以AOAB是等边三角形，所以ZAOB=60。，所以ZBAC+ZABC=30°,所以ZACB=150°答案：150\n49•考点：圆的综合题试题解析：(1)*•*OA=OB=m,/.0P=—AB=m；2(2)连结0C交OC于D,则OD最短，OC==5,AOD=OC-r=5-2=3.「.m的最小值为3.答案：(l)m；(2)3.50.考点：圆锥、圆柱的相关计算试题解析：解：扇形的弧长等于底面圆的周长得出2兀.设圆的半径是r,则鷲5,loU解得:r=3.故答案为：3.答案：351.考点：图形的旋转弧长计算试题解析：解：(1)AA.B.C,如图所示；(2)△A2B2C2如图所示；(3)Cj(1,4),C2(1,-4),根据勾股定理，OC=A/12+42=^,过C、0、C2三点的圆的圆弧是以CC2为直径的半圆，瓦可故答案为：(1,4)；(1,-4)；V177r.neie|||||«\n答案：见解析\n50.考点：统计图的分析平面直角坐标系及点的坐标直线与圆的位置关系试题解析：解：(1)1S1树状图得：则点Q所有可能的坐标有：(0,・2),(0,0),(0,1),(-2,,-2),(-2,0),(-2,1)；(2)J点Q在x轴上的有：(・2,0),・••点Q在x轴上的概率为：三6(3)VOO的半径是2,(-2,0),在OO上的有(0,・2),49・・・过点Q能作。。切线的概率为：―・••在OO外的有(-2,1),(・2,・2)答案：见解析53•考点：圆的综合题试题解析：解：VOE丄AB,・•・ZOEF=90°,VOC为小圆的直径，・・・ZOFC=90°,而ZEOF=ZFOC,ARtAOEF^RtAOFC,・・・OE：OF=OF：OC,即4：6=6：OC,・・・G)O的半径OC=9；在RtAOCF中，OF=6,OC=9,•••CF=V0C2-0F2=3V5，VOF丄CD,・・・CF=DF,CD=2CF=6V5・答案：见解析54.考点：切线的性质与判定试题解析：(1)证明：TAB是OO的切直径，AZADB=90°,又・・・ZBAD=ZBED,ZBED=ZDBC,・・・ZBAD=ZDBC,・・・ZBAD+ZABD=ZDBC+ABD=90°,.•.ZABC=90°,ABC是OO的切线；(2)解：VZBAD=ZDBC,ZC=ZC,AAABC^ABDC,\nACA=BC，即BC=AC・CD=(AD+CD)・CD=10,.\BC=V10.答案：见解析54.考点：切线的性质与判定圆周角定理及推论试题解析：解：TPA,PB分别切(DO于A,B点，AC是(DO的直径，・・・ZPAC=90。，PA=PB,又VZP=50°,180°-50°・•・ZPAB=ZPBA=65°,ZBAOZPAC-ZPAB=90°-65°=25°.2答案：25°55.考点：角及角平分线切线的性质与判定阴影部分图形的相关计算试题解析：试题解析：(1)证明：连接OD.VBC是OO的切线，D为切点，AOD丄BC.又TAC丄BC,・・・OD〃AC,・・・ZADO=ZCAD.又・.・OD=OA,.\ZADO=ZOAD\n:.ZCAD=ZOAD,即AD平分ZBAC.EDAB(2)方法一：连接OE,ED.•••ZBAO60。，OE=OA,•••△OAE为等边三角形，・•・ZAOE=60°,•••ZADE=30°.又.・ZCMD-|ziMC-3r,AZADE=ZOAD,•••阴影部分的面积=S^ODE=fiOxjrx43fi0方法二：同方法一，得ED〃AO,・・・四边形AODE为平行四边形，•••ED〃AO,乂S和形ODE—Sz\.OED=—事■—石_・•・阴影部分的面积=(S^ODE—SaOED)+S/.AED=|>--.答案：(1)见解析；(2)54.考点：圆的综合题试题解析：(1)连接OE,OC；如图所示：VDE与OO相切于点E,AZOEC=90°,在厶OBC和ZiOEC中，VOB=OE,CB=CE,OC=OC,AAOBC^AOEC(SSS),AZOBC=ZOEC=90°,ABC为。0的切线；(2)过点D作DF丄BC于F；如图所示：设CE=x,VCE,CB为(DO切线，ACB=CE=x,VDE,DA为G)O切线，DE=DA=1,・・・DOx+l,VZDAB=ZABC=ZDFB=90°,二四边形ADFB为矩形，DF=AB=4BF=AD=1,・・・FC=x-1,RtACDF屮，根据勾股定理得：(x+l)3-(l-lf=16,解得：x=4,\n答案：（1）证明见试题解析；（2）4.54.考点：圆的综合题试题解析：（1）解：•:AB是OO直径，C7在00±,二厶3=90°又tBC=3.AB=5・：・AC=4（2）证明：-AC是4M8的角平分线，二又vAD丄DC,.：ZX£X7=ZXCT=9・•・雨刮杆AB扫过的最大面积S=in:(OB2-OA2)=1392ti.答案：见解析54.考点：切线的性质与判定锐角三角函数圆周角定理及推论试题解析：(1)证明：如图，连接OD,B(2)解：如图，连接BD,BVAD为ZCAB的平分线，JZCAD=ZBADo又OA=OD,•••ZBAD=ZODAo•••ZCAD=ZODA。・・・AC〃OD。•••ZE+ZEDO180。。又AE丄ED,即ZE=90°,ZEDO=90°o•••OD为圆O的切线。VAB为圆O的直径，•••ZADB=90°oAR4在RtAAED中，AE=4,AD=5,AcosZEAD-—--oAD54XVZEAD=ZDAB,在RtAABD中，Ac«Z：DAB-—=1-AB5AAB=-AD=-x5=—,即圆的直径为兰。4444答案：见解析62•考点：圆的综合题试题解析：证明：(1)VBD平分ZCBA,\n・•・ZCBD=ZDBA,・・・ZDAC与ZCBD都是弧CD所对的圆周角，AZDAC=ZCBD,.\ZDAC=ZDBA,VAB是OO的直径，DE丄AB,AZADB=ZAED=90°,・•・ZADE+ZDAE=90°,ZDBA+ZDAE=90°,AZADE=ZDBA,.\ZDAC=ZADE,・・・ZDAC=ZDBA；(2)证明：TAB为直径，・・・ZADB=90。，VDE丄AB于E,/.ZDEB=90°,・•・ZADE+ZEDB=ZABD+ZEDB=90°,・•・ZADE=ZABD=ZDAP,APD=PA,•・•ZDFA+ZDAC=ZADE+ZPDF=90°,且ZADB=90°,.•.ZPDF=ZPFD,・・・PD=PF,・・・PA=PF,即P是线段AF的中点;B(3)解：连接CD,VZCBD=ZDBA,・・・CD=AD,TCD二3,・・・AD=3,VZADB=90°,・・・AB=5,故OO的半径为2.5,VDExAB=ADxBD,・・・5DE=3x4,・・・DE=2.4.即DE的长为2.4.答案：见解析\n63.考点：切线的性质与判左等腰三角形直角三角形与勾股世理圆周角左理及推论相似三角形判圧及性质试题解析：(1)证明：TBD是(DO的切线，・・・ZDBA=90°,TCH丄AB,・・・CH〃BD,AAAEC^AAFD,.AE^CE••・AE・FD=AF・EC.(2)证明：・・・CH〃BD,.•.AAEC^AAFD,AAHE^AABF,.CE=AE=EH，，DF_AF^BF，VCE=EH(E为CH中点)，・・・BF=DF,TAB为OO的直径，.\ZACB=ZDCB=90o,.\CF=DF=BF,即CF=BF.(3)解：•.*BF=CF=DF(已证)，EF=BF=2,・・・EF=FC,AZFCE=ZFEC,VZAHE=ZCHG=90°,・•・ZFAH+ZAEH=90°,ZG+ZGCH=90°,・・•ZAEH=ZCEF,AZG=ZFAG,AAF=FG,VFB丄AG,・・・AB=BG,连接OC,BC,VBF切OO于B,AZFBC=ZCAB,VOC=OA,CF=BF,・•・ZFCB=ZFBC,ZOCA=ZOAC,AZFCB=ZCAB,•・・ZACB=90°,\n.\ZACO+ZBCO=90o,・・・ZFCB+ZBCO=90。，即OC丄CG,\n・・・CG是（DO切线，VGBA是。0割线，FB=FE=2,由切割线定理得：（2+FG）2=BGxAG=2BG【在RtABFG中，由勾股定理得：BG=FG2-BF2,2AFG-4FG-12=0,解得：FG=6,FG=-2（舍去），由勾股定理得：AG=BG=(6°-2?=4近,・・・00的半径是2竝答案：见解析63.考点：切线的性质与判定相似三角形判定及性质试题解析：(1)证明：・.・AB〃CD.\ZABC4-ZBCD=180°TAB、BC、CD分别与相切于E、F、G,・・・B0平分ZABC,CO平分ZDCB,・•・ZOBO*ZABC，ZOCB=*ZDCB,:.ZOBC+ZOCB=-i(ZABC+ZDCB)=X180°=90°,・•・ZBOC=90°,・・・B0丄CO.(2)解：连接OF,则OF1BC,・・・RTABOF^RTABCO,.BF=BO••莎丽•・•在RTABOF中，B0=6cm,C0=8cm,BC=J62+8'=1Ocm,・BF_6•■—,610•:BF=3.6cm,TAB、BC、CD分别与（DO相切,ABE=BF=3.6cm,CG=CF,VCF=BC-BF=10-3.6=6.4cm.\n/•CG=CF=6.4cm.答案：见解析63.考点：切线的性质与判定直角三角形与勾股定理垂径定理及推论圆周角定理及推论试题解析：（1）证明：连接0D,如图1所示：VOD=OC,・・・ZDCB=ZODC,XZDOB为厶COD的外角,・•・ZDOB=ZDCB+ZODC=2ZDCB,又VZA=2ZDCB,.\ZA=ZDOB,VZACB=90°,AZA+ZB=90°,AZDOB+ZB=90°,・・・ZBDO=90。，・・・0D丄AB,AAB是OO的切线；（2）解法一：过点0作0M丄CD于点M,如图1,VOD=OE=BE=-^BO,ZBDO=90°,AZB=30°,.\ZDOB=60o,VOD=OC,AZDCB=ZODC,又・・・ZDOBODC的外角，・・・ZDOB=ZDCB+ZODC=2ZDCB,・・・ZDCB=30。,•・•在RtAOCMZDCB=30°,OM=1,・・・OC=2OM=2,\n・・・OD=2,BO=BE+OE=2OE=4,・••在RtABDO'P，根据勾股定理得：BD=2a/3；解法二：过点0作0M丄CD于点M,连接DE,如图2,VOM丄CD,ACM=DM,又O为EC的中点，AOM为厶DCE的中位线,且0M=l,ADE=2OM=2,•・•在RtAOCM中，ZDCB=30°,OM=1,・•・OC=2OM=2,VRtABDO中，OE=BE,・・・DE冷BO,ABO=BE+OE=2OE=4,・・・OD=OE=2,在RtABDO中，根据勾股定理得BD=2a/3.CA答案：见解析66.考点：图形的旋转扇形面积的计算图形的平移试题解析：解：(1)如图所示：(2)由厶ADG在坐标系中的位置可知，A.(0,2):C,(2,0):(3)旋转后的图形如图所示：\n*•*由勾股定理可知，BiCi=^/J2-I-42=V17»答案：见解析67•考点：图形的旋转弧长计算图形的平移试题解析：解:(1)如图，△AiBiG即为所求;(2)如图，AA2B2C2即为所求；由勾股定理得，0A=V巨讦,点A旋转到点A?所经过的路径长为:180290■兀*VT7_V17兀答案：见解析6&考点：与圆有关的概念及性质\n试题解析：(1)如图1,点P就是所求作的点;(2)如图2,CD为AB边上的高.答案：见解析69.考点：解直角三角形的实际应用弧反计算试题解析：解：(1)过A作AD丄BC于点D,V0A=0B=3m,AB=3+3=6m,・•・AD=AB*sin15^6x0.26=1.6；(2)如图所示，A点的运动路线是以点O为圆心，以OA的长为半径的奩的长.连接OD,TO是AB的中点，・・・OD=OA=OB,AZAOD=2ZB=30o,・・・A运动路线长=■30X兀><3=兀~~180~=_2答案：见解析70.考点：图形的旋转全等三角形的判定扇形血积的计算图形的平移试题解析：证明：°・・AB〃CD,・•・ZA=ZC.JAE=CF,・・・AE+EF=CF+EF,即AF=CE.又•・・AB=CD,・•・AABF^ACDE.（2）解：①如图所示\n②如图所示;在旋转过程中，线段A©所扫过的面积等于當=4r答案：见解析