- 2022-09-08 发布 |
- 37.5 KB |
- 9页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学竞赛几何练习题集
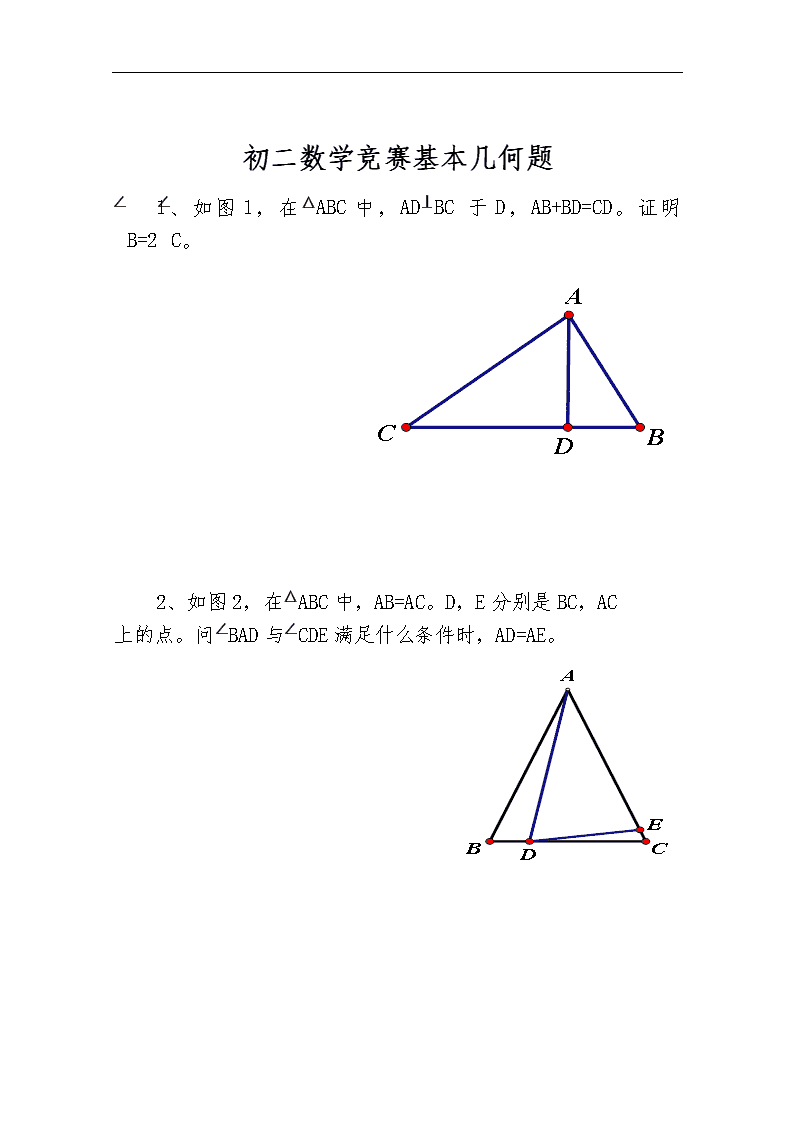
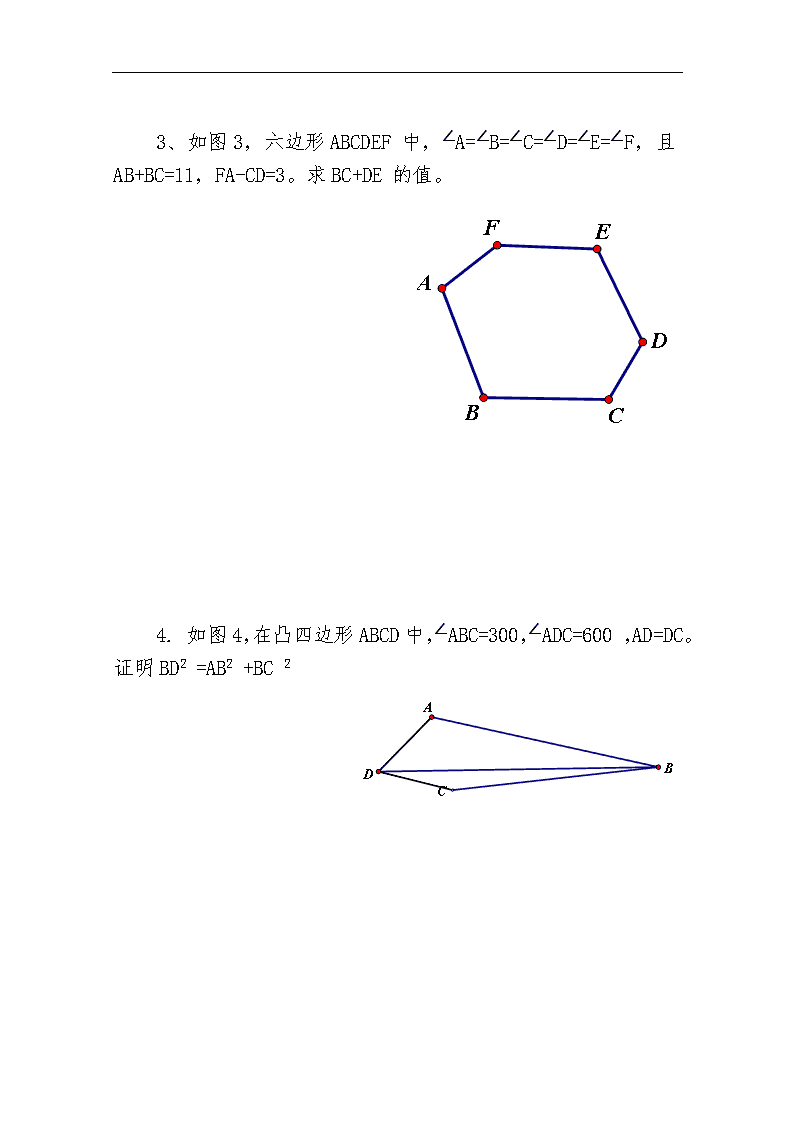
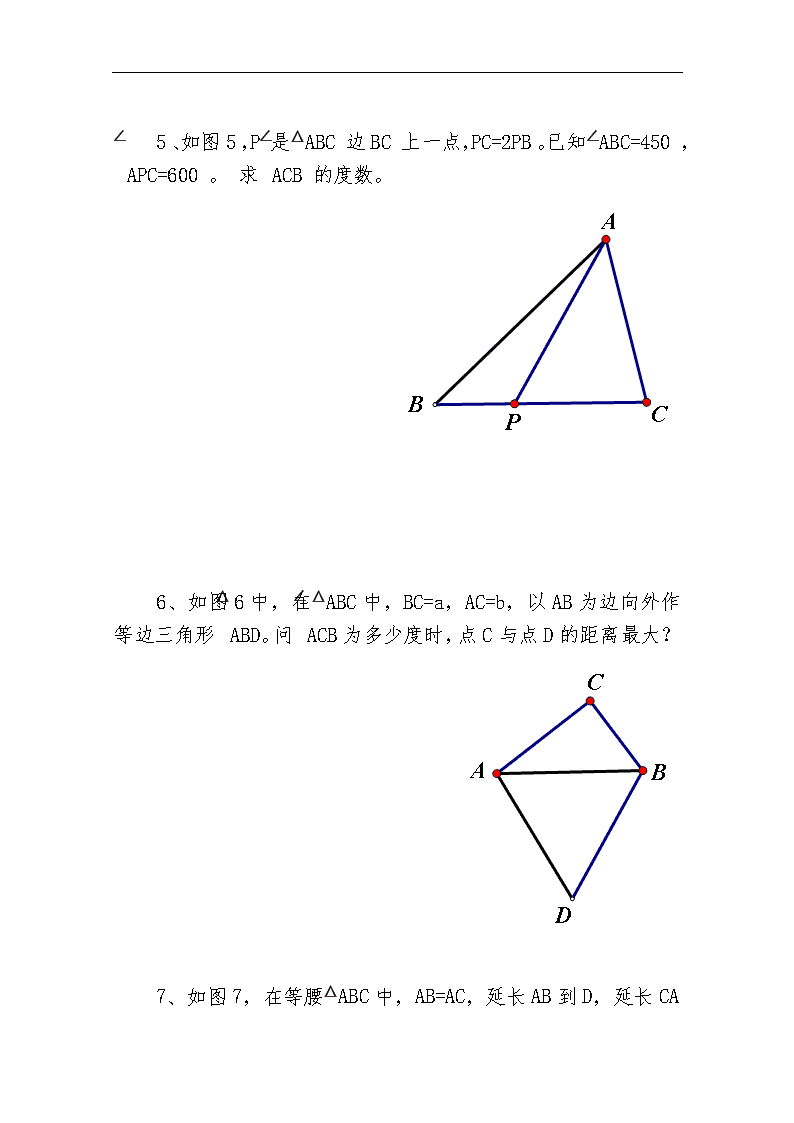
初二数学竞赛基本几何题1、如图1,在△ABC中,AD⊥BC于D,AB+BD=CD。证明∠B=2∠C。2、如图2,在△ABC中,AB=AC。D,E分别是BC,AC上的点。问∠BAD与∠CDE满足什么条件时,AD=AE。\n3、如图3,六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11,FA-CD=3。求BC+DE的值。4.如图4,在凸四边形ABCD中,∠ABC=300,∠ADC=600,AD=DC。证明BD2=AB2+BC2\n5、如图5,P是△ABC边BC上一点,PC=2PB。已知∠ABC=450,∠APC=600。求∠ACB的度数。6、如图6中,在△ABC中,BC=a,AC=b,以AB为边向外作等边三角形△ABD。问∠ACB为多少度时,点C与点D的距离最大?7、如图7,在等腰△ABC中,\nAB=AC,延长AB到D,延长CA到E,连DE,有AD=BC=CE=DE。证明:∠BAC=100°。8、如图8,在△ABC中,AD是边BC上的中线,AB=√2,AD=√6,AC=√26。求∠ABC的度数。9、如图9,在△ABC的外面作正方形ABEF和ACGH,AD⊥BC于D。延长DA交FH于M。证明:FM=HM。\n10、如图10,P,Q,R分别是等边△ABC三条边的中点。M是BC上一点。以MP为一边在BC同侧作等边△PMS。连SQ。证明RM=SQ.11、如图11,在四边形ABCD中,AB=a,AD=b,BC=CD.对角线AC平分∠BAD。问a与b符合什么条件时,有∠D+∠B=180°\n12、如图12,在等腰△ABC中,AD是边BC上的中线,E是△ADB内任一点,连AE,BE,CE。证明:∠AEB>∠AEC。13、如图,在凸四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°证明:BC+CD=AC。\n14、如图14,在△ABC中,AD是边BC上的中线,点M在AB上,点N在AC上。已知∠MDN=90°,BM2+CN2=DM2+DN2。证明:AD2=1/4(AB2+AC2)15、如图,在△ABC中,∠A=90°AD垂直BC交于D,∠BCA的平分线交AD于F,交AB于E,FG∥BC,交AB于G,AE=4,AB=14,求BG的长。\n16.如图Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于D,作CE垂直BD交BD延长线于E,过A作AH⊥BC交BD于M,试猜想BM与CE的大小关系,并证明你的结论。\n您好,欢迎您阅读我的文章,本WORD文档可编辑修改,也可以直接打印。阅读过后,希望您提出保贵的意见或建议。阅读和学习是一种非常好的习惯,坚持下去,让我们共同进步。您好,欢迎您阅读我的文章,本WORD文档可编辑修改,也可以直接打印。阅读过后,希望您提出保贵的意见或建议。阅读和学习是一种非常好的习惯,坚持下去,让我们共同进步。查看更多