- 2022-09-08 发布 |
- 37.5 KB |
- 2页

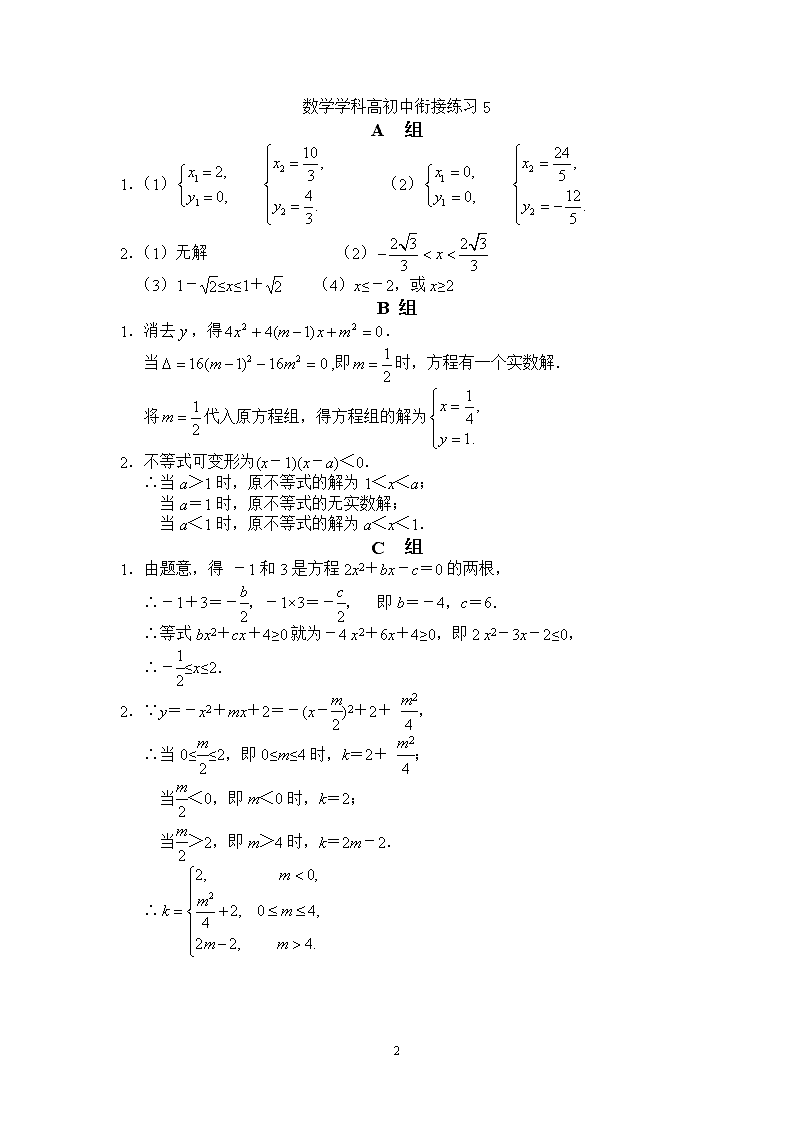
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学学科高初中衔接练习5
数学学科高初中衔接练习5A组1.解下列方程组:(1)(2)2.解下列不等式:(1)3x2-2x+1<0;(2)3x2-4<0;(3)2x-x2≥-1;(4)4-x2≤0.B组1.取什么值时,方程组有一个实数解?并求出这时方程组的解.2.解关于x的不等式x2-(1+a)x+a<0(a为常数).C组1.已知关于x不等式2x2+bx-c>0的解为x<-1,或x>3.试解关于x的不等式bx2+cx+4≥0.2.试求关于x的函数y=-x2+mx+2在0≤x≤2上的最大值k.2\n数学学科高初中衔接练习5A组1.(1)(2)2.(1)无解(2)(3)1-≤x≤1+(4)x≤-2,或x≥2B组1.消去,得.当,即时,方程有一个实数解.将代入原方程组,得方程组的解为2.不等式可变形为(x-1)(x-a)<0.∴当a>1时,原不等式的解为1<x<a;当a=1时,原不等式的无实数解;当a<1时,原不等式的解为a<x<1.C组1.由题意,得-1和3是方程2x2+bx-c=0的两根,∴-1+3=-,-1×3=-,即b=-4,c=6.∴等式bx2+cx+4≥0就为-4x2+6x+4≥0,即2x2-3x-2≤0,∴-≤x≤2.2.∵y=-x2+mx+2=-(x-)2+2+,∴当0≤≤2,即0≤m≤4时,k=2+;当<0,即m<0时,k=2;当>2,即m>4时,k=2m-2.∴2查看更多