- 2022-09-07 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学竞赛精品标准教程及练习 70份 初中数学竞赛精品标准教程及练习61:函数的图象
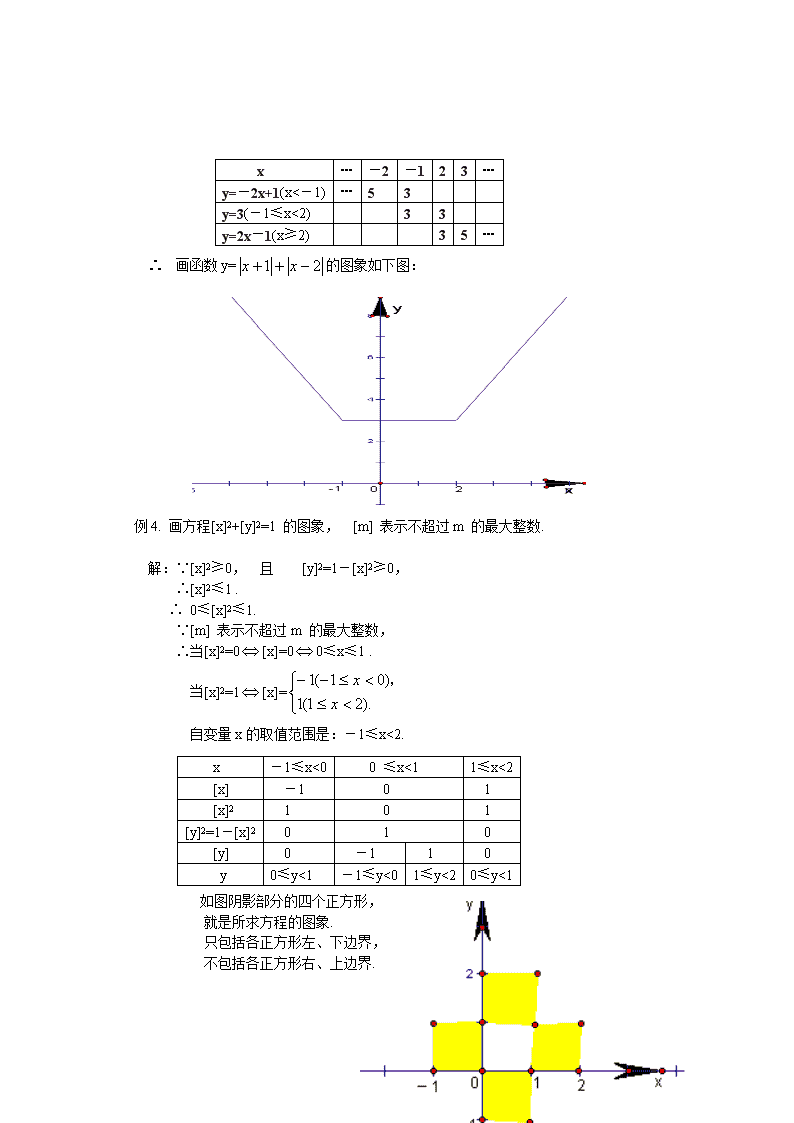
初中数学竞赛精品标准教程及练习(61) 函数的图象一、内容提要1.函数的图象定义:在直角坐标系中,以自变量x为横坐标和以它的函数y的对应值为纵坐标的点的集合,叫做函数y=f(x)的图象.例如一次函数y=kx+b(k,b是常数,k≠0)的图象是一条直线l.①l上的任一点p0(x0,y0)的坐标,适合等式y=kx+b,即y0=kx0+b;②若y1=kx1+b,则点p1(x1,y1)在直线l上.2.方程的图象:我们把y=kx+b看作是关于x, y的二元一次方程kx-y+b=0, 那么直线l就是以这个方程的解为坐标的点的集合,我们把这条直线叫做二元一次方程的图象.二元一次方程ax+by+c=0(a,b,c是常数,a≠0,b≠0)叫做直线方程. 一般地,在直角坐标系中,如果某曲线是以某二元方程的解为坐标的点的集合,那么这曲线就叫做这个方程的图象. 例如:二元二次方程y=ax2+bx+c(a≠0)(即二次函数)的图象是抛物线;二元分式方程y=(k≠0)(即反比例函数)的图象是双曲线.3.函数的图象能直观地反映自变量x与函数y的对应规律. 例如:①由图象的最高,最低点可看函数的最大,最小值;②由图象的上升,下降反映函数y是随x的增大而增大(或减小);③函数y=f(x)的图象在横轴的上方,下方或轴上,分别表示y>0,y<0,y=0.图象所对应的横坐标就是不等式f(x)>0,f(x)<0的解集和方程f(x)=0的解.④两个函数图象的交点坐标,就是这两个图象所表示的两个方程(即函数解析式)的公共解.等等4.画函数图象一般是:①应先确定自变量的取值范围. 要使代数式有意义,并使代数式所表示的实际问题有意义,还要注意是否连续,是否有界.②一般用描点法,但对一次函数(二元一次方程)的图象,因它是直线(包括射线、线段),所以可采用两点法.线段一定要画出端点(包括临界点).③对含有绝对值符号(或其他特殊符号)的解析式,应按定义对自变量分区讨论,写成几个解析式.二、例题例1. 右图是二次函数y=ax2+bx+c (a≠0),试决定a, b, c及b2-4ac的符号.解:∵抛物线开口向下, ∴a<0.∵对称轴在原点右边,∴x=->0且a<0,∴b>0.∵抛物线与纵轴的交点在正半轴上, ∴截距c>0.∵抛物线与横轴有两个交点, ∴b2-4ac>0.例2.已知:抛物线f:y=-(x-2)2+5. \n试写出把f向左平行移动2个单位后,所得的曲线f1的方程;以及f关于x轴对称的曲线f2的方程. 画出f1和f2的略图,并求:(1)x的值什么范围,曲线f1和f2都是下降的;(2)x的值在什么范围,曲线f1和f2围成一个封闭图形;(3)求在f1和f2围成封闭图形上,平行于y轴的线段的长度的最大值.解:f1 :y=-x2+5 (由顶点横坐标变化确定的),f2:y=(x-2)2-5(由开口方向相反确定的). (1)当x≥0时,f1下降,当x≤2时,f2下降,∴当0≤x≤2时,曲线f1和f2都是下降的. (2)求两曲线的交点横坐标,即解方程组x2-2x-3=0.∴x=-1;或x=3. ∴当-1≤x≤3时,曲线f1和f2围成一个封闭图形.(3)封闭图形上,平行于y轴的线段的长度,就是对应于同一个横坐标,两曲线上的点的纵坐标的差.在区间–1≤x≤3内,设f1上的点P1(x,y1), f2上的点P2(x,y2),求y1-y2的最大值,可用配方法:y1-y2 = (-x2+5)-[(x-2)2-5]=-2x2+4x+6 =-2(x-1)2+8. ∵-2<0, ∴y1-y2有最大值.当x=1时,y1-y2的值最大是8.即线段长度的最大值是8.例3. 画函数y=的图象.解:自变量x的取值范围是全体实数,下面分区讨论:当x<-1时, y=-(x+1)-(x-2)=-2x+1;当-1≤x<2时, y=x+1-(x-2)=3;当x≥2时, y=x+1+x-2=2x-1. 即y==\nx…-2-123…y=-2x+1(x<-1)…53y=3(-1≤x<2)33y=2x-1(x≥2)35… ∴ 画函数y=的图象如下图:例4.画方程[x]2+[y]2=1的图象,[m]表示不超过m的最大整数.解:∵[x]2≥0, 且 [y]2=1-[x]2≥0, ∴[x]2≤1. ∴0≤[x]2≤1.∵[m]表示不超过m的最大整数,∴当[x]2=0[x]=00≤x≤1.当[x]2=1[x]=自变量x的取值范围是:-1≤x<2.x-1≤x<00≤x<11≤x<2[x]-101[x]2101[y]2=1-[x]2010[y]0-110y0≤y<1-1≤y<01≤y<20≤y<1如图阴影部分的四个正方形,就是所求方程的图象.只包括各正方形左、下边界,不包括各正方形右、上边界.\n例5. 直线y=x+m与双曲线y=在第一象限相交点A,SRt△AOB=3.①求m的值;②设直线与x轴交于点C,求点C的坐标; ③求S△ABC.解:①设A坐标为 (x, x+m).∵S△AOB=OB×BA.∴整理得 ∴m=6②∵直线与x轴交于点C.把y=0代入y=x+6得x=-6,∴点C的坐标是(-6,0)③∵直线y=x+m与双曲线y=在第一象限相交点A,解方程组 得即点A的坐标是 (-3+,3+).∴BC==3+∴S△ABC=(3+)(3+)=12+3.例6.选择题(只有一个正大确的答案).①函数y=kx+k与y=在同一坐标系中的图象的大体位置是 ()\n ②函数y=1-的图象是( ) 解:①常数k是同一个值,.双曲线y= 在一、三象限,k>0, 那么y=kx+k中,当k>0时,直线上升且在y轴上的截距为正. 所以应选 (D); ②注意到y=1-中,当x=0和x=1时y有最大值1,故选 (A).三、练习611.填空:①横坐标为-2的点的集合,记作直线_____,纵轴记作直线______,横轴记作直线_____,横坐标与纵坐标互为相反数的点的集合是直线______,经过一、三象限,平分两坐标轴夹角的直线记作方程_______.②点P(x, y)关于横轴的对称点P1的坐标是( ),点P关于原点的对称点P2的坐标是( ).③ f:y=3(x-2)2+5,关于横轴对称的抛物线f1记作_______f关于原点对称的抛物线f2记作_______.④A(1,3)关于直线y=x的对称点A,的坐标是( ).点B(-2,3)关于直线y=-x的对称点B,的坐标是( ).2.根据图象位置判断指定的常数的符号①直线y=kx+b经过二、一、四象限,则k,b的符号是______②抛物线y=ax2+bx+c的位置,如图所示,试确定下列代数式的符号 a__,-______,b______,c_______,\nb2-4ac______,___________3.选择题(只有一个正确的答案)(1)下图(1)是一次函数px+qy+r=0的图象,下列条件正确的是( ).(A)p=q, r=0. (B)p=-q, r=0. (C)p=q, r=1. (D)p=-q,r=1.(2)下图(2)是二次函数y=ax2+bx+c的图象,如下答案哪个正确?( )(A)a+b+c=0. (B)a+b+c<0. (C)a+b+c>0. (D)a+b+c值不定.(1)(3)二次函数y=a(x+m)2+n中,a>0,m>0,n>0它的图象( ) (4)两个一次函数y=mx+ny=nx+m且mn<0,那么它们在同一坐标系内的图象大致为( )5(D)\n(5)在同一坐标系内,y=ax+b与y=ax2+b的图象大体位置是( ) (6)已知函数y+ax+b和y=ax2+bx+c那么它们的图象是( ))(x-6×)(x+2×=0.2)(xf-54. 画下列函数的图象①y=; ②y=; ③y=()2; ④ y=-.5. 有m部同样的机器,同时开始工作,需要m小时完成某项任务.设由x部机器完成某一任务,求所需的时间y(小时)与机器台数x(x为小于m的整数)的函数关系,并画出当m=5时函数的图象.6. 画如下方程、函数的图象.①;②y=x2-2|x|-3.7. 这是一张追及图看图回答: ① 谁追及谁? ② 谁早出发,早几小时? ③ 甲、乙在这段路程速度各多少? ④ 追的人从出发到追上,用了几小时?走多少路程? ⑤ 分别列出甲、乙两人的路程y甲,y乙和时间x的函数关系的解析式.\n8. 如图,抛物线L1:y=ax2+2bx+c和抛物线L2:y=(a+1)x2+2(b+2)x+c+3的位置如图所示.①.判断哪条抛物线经过A、B、C三点,说明理由;②.求出点B和点C的横坐标;③.若AB=BC,OC=OD,求a, b, c的值.9. 坐标平面上,纵坐标与横坐标都是整数的格点(整点),试在二次函数y=-1CBDA1的图象上找出满足y的所有整点(x,y),并说明理由. (8)练习61参考答案:1. ①x=-2, x=0, y=0, y=-x, y=x; ②(x,y),(-x,-y); ③y=-3(x-2)2-5, y=-3(x+2)2-5 ④(3,1),(-3,2) 2. ①k<0, b>0. ②正,负,正,负,负,正,负.3. ①(A), ②(B), ③(B), ④(C), ⑤(D), ⑥(C) \n4. ①∵x≠0,∴图象不以过原点;② y≥0;③x≥0;④ y≤0.5. y=(x是正整数x≤m=5).6. (如图) 7. ①乙追及甲; ②甲先1小时; ③时速甲4、乙5千米; ④乙用4小时追上甲先走的4千米 ⑤y甲=4x,y乙=5x 8. ①∵由图象a,a+1异号,∴L2过A,B,C三点. ②-3,-1. ③-,0,.9. (2,2),(4,3),(7,6),(9,9),(-3,3),(-6,6). 由x2-x+18≤10.当x≥0时,x2-x+18≤10x,x2-11x+18≤0,(x-2)(x-9)≤0,2≤x≤9, 这时,有4个整数点:(2,2),(4,3),(7,6),(9,9);当x<0时,x2-x+18≤-10x, x2+9x+18≤0, (x+6)(x+3)≤0,-6≤x≤-3,这时有两个整数点:(-3,3),(-6,6).\n查看更多