- 2022-09-07 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学竞赛精品标准教程及练习70份初中数学竞赛精品标准教程及练习42型如 的证明
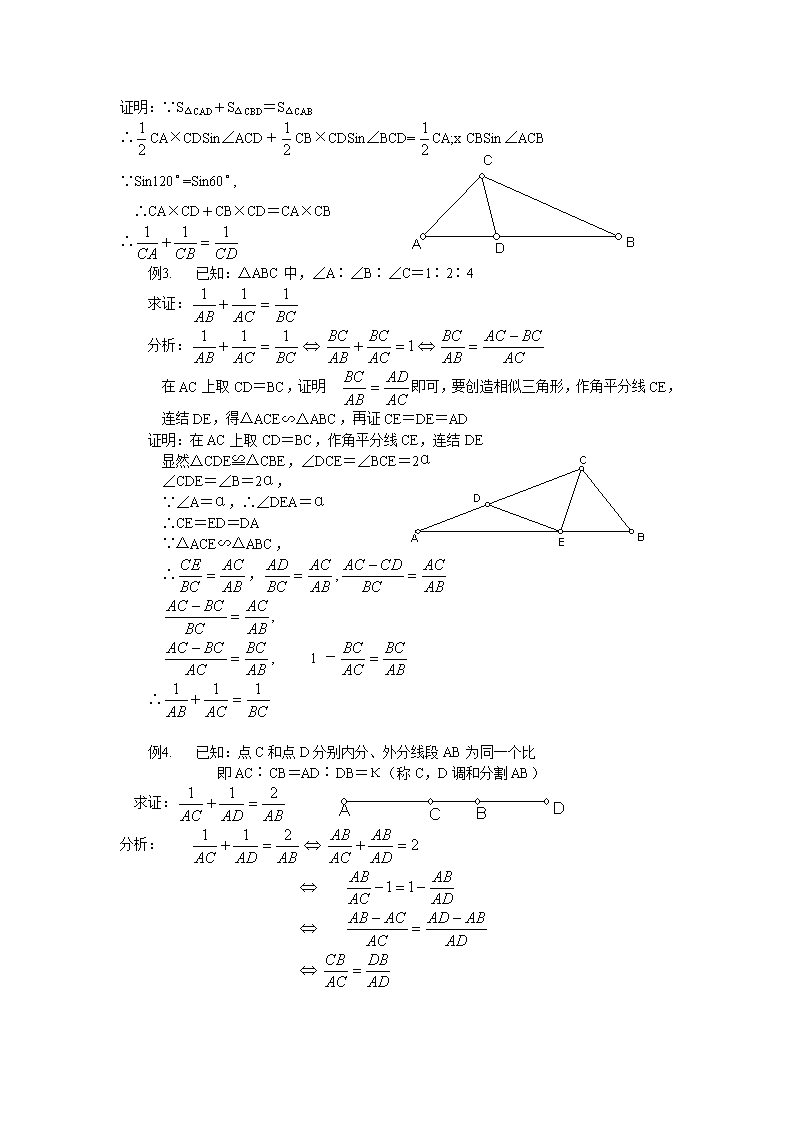
初中数学竞赛精品标准教程及练习(42)型如的证明一、内容提要型如的证明,通常是证明它的等价命题第一种转化为线段的比例式(1)可证 和两个同分母的分式分别相等,例如 当m+n=p 时等式成立(2)可证明 c,a,b-c,b四条线段成比例,关鍵是作出b-c的差(3)可证明 a+b,a,b,c四条线段成比例,关鍵是作出a+b的和第二种 转化为线段的乘积式bc+ac=ab(4)(4)常用两个图形的面积和等于另一个图形的面积二、例题例1.已知:在梯形ABCD中,AB∥CD,O是AC和BD的交点,OE∥AB交BC于有E求证:分析:证明,分别和,相等即可(下略)例2.已知:在△ABC中,∠ACB=120,CD是角平分线求证:分析一:延长AC到E,使CE=CB,可证△BCE为等边,BE∥CD分析二:=在CB上截取CE=CD,可证△CDE为等边三角形,DE∥CA分析三:CA×CD+CB×CD=CA×CB可由S△CAD+S△CBD=S△CAB证得\n证明:∵S△CAD+S△CBD=S△CAB∴CA×CDSin∠ACD+CB×CDSin∠BCD=CA;xCBSin∠ACB∵Sin120=Sin60, ∴CA×CD+CB×CD=CA×CB∴例1.已知:△ABC中,∠A∶∠B∶∠C=1∶2∶4求证:分析:在AC上取CD=BC,证明 即可,要创造相似三角形,作角平分线CE,连结DE,得△ACE∽△ABC,再证CE=DE=AD证明:在AC上取CD=BC,作角平分线CE,连结DE显然△CDE≌△CBE,∠DCE=∠BCE=2α∠CDE=∠B=2α,∵∠A=α,∴∠DEA=α∴CE=ED=DA∵△ACE∽△ABC,∴,,,, 1-∴例2.已知:点C和点D分别内分、外分线段AB为同一个比 即AC∶CB=AD∶DB=κ(称C,D调和分割AB) 求证:分析: \n=κ(证明步骤是分析的倒逆)例1.如图已知:△ABC中,BC=a,高AD=h,内接正方形EFGH边长为m 求证:分析:hm+am=ah, 可用面积公式证证明:∵S△AEF+S梯形EFGH=S△ABC∴即 m(h-m)+(m+a)m=ah,mh+ma=ah 两边除以ahm, 得三、练习421.四边形ABCD中,∠A=∠C=Rt∠,P是BD上的一点,PM⊥AB,PN⊥CD,M,N是垂足,求证:2.△ABC中,CD是角平分线,DE∥BC交AC于E,则3.经过平行四边形ABCD的顶点D的一直线交BC于M,交AB的延长线于N,求证4.已知:△ABC中,D,E分别在边AB,AC上,且DE∥BC求证:(1∶S△BAE)+(1∶S△BEC)=1∶S△BED5.△ABC中,∠C=60,角平分线CD=t, 求证6.△ABC内一点P,PD⊥BC,PE⊥AC,PF⊥AB,D,E,F是垂足,设a,b,c 边上的高分别为ha,hb,hc求证7.已知2a=7b=14c 求证 8.已知:直线y=bx+c (b≠0), 与抛物线y=ax2(a≠0) 有两个交点,与横轴有一个交点,它们的横坐标分别为x1,x2,x3 且b2-4ac>0求证:\n1.Rt△ABC斜边上的高CD=h,那么2.过△ABC内一点P分别作三边的平行线DE∥BC,FG∥AB,HK∥AC求证:① ②11. 在等边△ABC外接圆的弧上取点PPA交BC于M,求证12.PA,PB切⊙O于A,B,直线PO交⊙O于M,N,交AB于C求证13.已知半径分别为R,r 的⊙O和⊙O1外切于P,点P到外公切线AB的距离为d, 则 练习42参考答案:4.利用等高的两个三角形面积的比等于它们的底的比1.S△ABC=abSinC2.连结PA,PB,PC由……8.x1,x2是方程bx+c=ax2 的两个根,由韦达定理得且x3是bx+c=0的根……9. 射影定理 11.用S△PBM+S△PCM=S△PBC12. AM,AN是△PAC的内,外角的平分线。查看更多