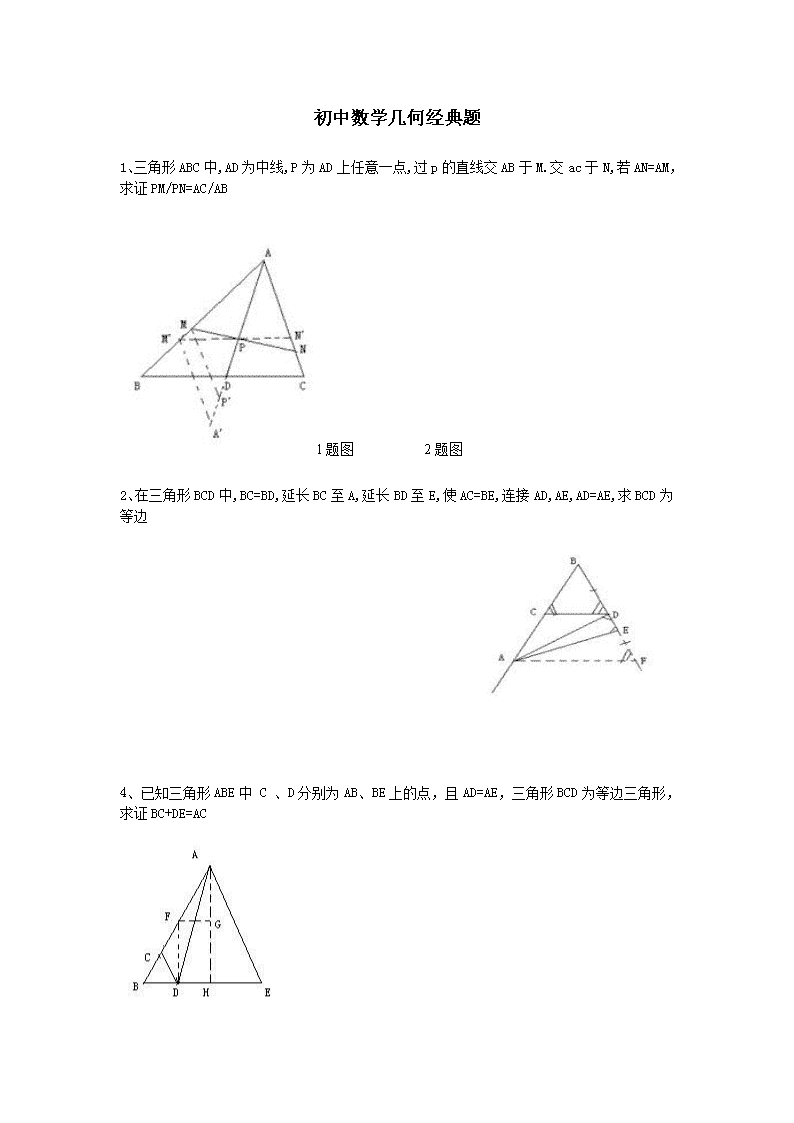初中数学几何经典题:测试题训练
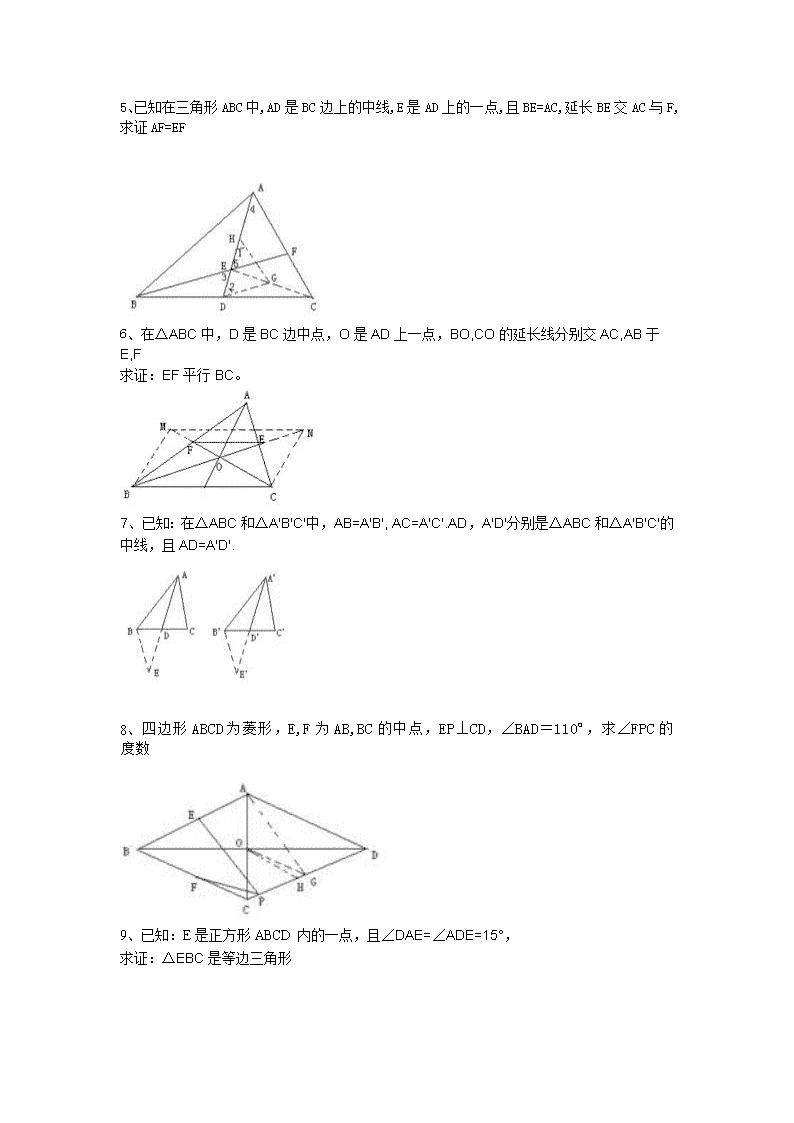
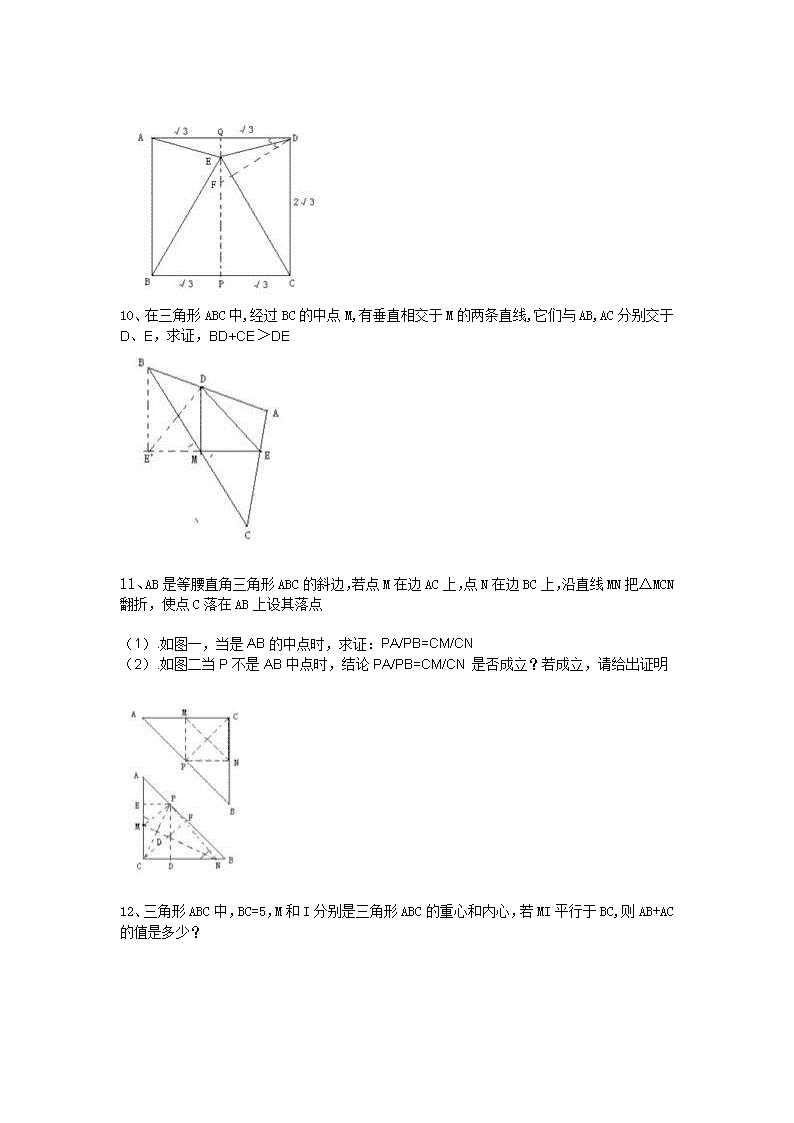
初中数学几何经典题1、三角形ABC中,AD为中线,P为AD上任意一点,过p的直线交AB于M.交ac于N,若AN=AM,求证PM/PN=AC/AB1题图2题图2、在三角形BCD中,BC=BD,延长BC至A,延长BD至E,使AC=BE,连接AD,AE,AD=AE,求BCD为等边4、已知三角形ABE中C、D分别为AB、BE上的点,且AD=AE,三角形BCD为等边三角形,求证BC+DE=AC\n5、已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF6、在△ABC中,D是BC边中点,O是AD上一点,BO,CO的延长线分别交AC,AB于E,F求证:EF平行BC。7、已知:在△ABC和△A'B'C'中,AB=A'B',AC=A'C'.AD,A'D'分别是△ABC和△A'B'C'的中线,且AD=A'D'.8、四边形ABCD为菱形,E,F为AB,BC的中点,EP⊥CD,∠BAD=110º,求∠FPC的度数9、已知:E是正方形ABCD内的一点,且∠DAE=∠ADE=15°,求证:△EBC是等边三角形\n10、在三角形ABC中,经过BC的中点M,有垂直相交于M的两条直线,它们与AB,AC分别交于D、E,求证,BD+CE>DE11、AB是等腰直角三角形ABC的斜边,若点M在边AC上,点N在边BC上,沿直线MN把△MCN翻折,使点C落在AB上设其落点(1).如图一,当是AB的中点时,求证:PA/PB=CM/CN(2).如图二当P不是AB中点时,结论PA/PB=CM/CN是否成立?若成立,请给出证明12、三角形ABC中,BC=5,M和I分别是三角形ABC的重心和内心,若MI平行于BC,则AB+AC的值是多少?\n14、已知:D.E位△ABC内的两点求证:AB+AC>BD+DE+EC15、在三角形ABC中,BD,CE是边AC,AB上的中点,BD与CE相交于点O,BO与OD的长度有什么关系?BC边上的中线是否一定过点O?为什么?17、三角形中线分别为91215求三角形面积18、在△ABC中∠A=90°,AD⊥BC于D,M是AD的中点,延长BM交AC于E,过E作EF⊥BC于F。求证:EF²=AE*CE\n19、已知E为平行四边形ABCD的边BC上的任一点,DE延长线交AB延长线与F,求证S△ABE=S△CEF。20、等腰直角三角形,角A为90°,D,E两点为斜边上的动点,角DAE=45°,当D合B重合或E和C重合时,线段DE的长度等于BD+EC当不重合时,DE
DE'等量代换得:BD+CE>DE11.(1)、证明:因为P是AB中点,所以:AP/PB=1,因为:P点是C点沿直线MN折叠的落点,所以:MN垂直平分PC,所以:CM=MP,由AP=BP得∠ACP=∠BCP=45°所以:CM=MN所以:CM/CN=1所以:PA/PB=CM/CN(2)、结论仍然成立。证明:过P点分别作AC,BC的垂线PE,PD.E,D是垂足。过C作CF垂直AB,F是垂足。则:S△APC=(1/2)AC*PE=(1/2)AP*CFS△BPC=(1/2)BC*PD=(1/2)BP*CF而AC=BC所以:PE/PD=AP/BP由∠MCN=∠MPN=90°知MCNP四点共元所以:∠PME=∠PND所以:RT△PEM∽RT△PDN所以:PE/PD=PM/PN而PM=MC,PN=NC所以:PE/PD=MC/NC所以:AP/BP=MC/NC12.解:设内心到三边的距离为r,BC边上的高为AE=h,如图。因为MI‖BC,AM=2MD所以:h=3r而:S△ABC=(1/2)BC*h=(5/2)h=(15/2)rS△ABC=S△ABI+S△BCI+S△ACE=(1/2))r(AB+AC+5)所以:(15/2)r=(1/2))r(AB+AC+5)解得:AB+AC=10\n14.证明:设直线DE交AB于F,交AC于G,则:在△AFG中,有AF+AG>FD+DE+EG在△BFD中,有BF+FD>BD在△EGC中,有EG+GC>EC所以:三个不等式两边相加得AF+AG+BF+FD+EG+GC>FD+DE+EG+BD+EC即:AB+AC>DE+BD+EC15.答:BO=2DO,BC边上的中线过O点。证明:连接AO,设M,N分别是BO,CO的中点,连接EM,DN,则:EM平行并等于AO的一半,DN平行并等于AO的一半所以:EM平行并等于DN所以:四边形EMND是平行四边形所以:MO=OD所以:BM=MO=OD所以:BO=2DO延长AO交BC于G,延长DN交BC于H,延长EM交BC于Q,则:由AG‖EQ‖DH,BM=MO=OD得知BQ=QG=GH=HC所以;BG=GC所以;BC边上的中线过O点。17.解:过F点作AE的平行线,交DC于H点,则:FH=(1/2)AM=5,MH=3,(三角形中位线定理,三中线交点分中线性质)而:MF=4所以:三角形FMH是直角三角形,即BM⊥DC.所以:S△BCD=(1/2)*9*8=36,所以:S△ADC=S△BCD=36(同高等底的两个三角形面积相等)所以:S△ABC=7218.证明:如图,延长BA,FE交于N.因为:AD‖FN所以:AM/NE=BM/BE,MD/EF=BM/BE所以:AM/NE=MD/EF而:AM=DM所以:NE=EF由于:角NAC=∠NFC=90°所以:AFCN四点共圆所以:AE*EC=EF*EN所以:EF^2=AE*EC\n19证明:分别过C,E两点作AB的垂线CH,EG,H,G是垂足。设BE=m,EC=n由△BFE∽△CDE得:BF/CD=m/n.即BF/(BF+CD)=m/(m+n)也就是BF/AF=m/(m+n)(因为AB=CD,有AF=BF+CD)由RT△BEG∽RT△BCH得:HC/GE=(m+n)/m所以:(BF/CD)*(HC/GE)=1而:S△AFE=(1/2)AF*GES△BFC=(1/2)BF*CH所以:S△BFC/S△AFE=BF*HC/AF*GE=1所以:S△BFC=S△AFE两边同时减去S△BFE得:S△ABE=S△CEF。20.证明:不重合时。以A点为顶点,AC为一边向△ABC的外侧作∠CAB',使∠CAB'=∠DAB.截取AB'=AD.又因为:AC=AB.所以:△CAB'≌△BAD所以:B'C=DB因为:∠BAC=90°,∠DAE=45°。所以:∠BAD+∠CAE=45°。所以:∠B'AE=∠B'AC+∠CAE=45°=∠EAD.又AD=AB',AE=AE所以:△B'AE≌△DAE所以:DE=EB'在△ECB'中,有EB'
查看更多